混沌粒子群算法-高斯过程回归的SOH估计

丁一，刘盛终，王旭东，霍现旭，胡志刚，姜帆

（1.国网天津市电力公司电力科学研究院，天津 300384；2.国网天津市电力公司，天津300010；3.国网天津市电力公司城东供电分公司，天津 300250；4.国网天津市电力公司蓟州供电分公司，天津 301900）

铅酸蓄电池被广泛应用在电动汽车、光伏电站、分布式电源和航空航天等领域中，其维护简单，使用寿命长，功率高，稳定性和可靠性较强。健康状态（SOH）是铅酸蓄电池的一个重要指标，它反映了电池的老化程度，也是电池管理系统（battery management system，BMS）建设中需要重点考察的因素。通常认为电池出厂时SOH为100%，随着循环充放电次数的增多，其可用容量逐渐递减，这一过程是不可逆的，SOH的定义式为电池的当前可用容量与电池出厂容量的比值。当SOH下降到特定数值以下时，一般为0.8左右，电池报废。

当前对于铅酸蓄电池SOH估计的研究文章较多，一般SOH估计分为三大类：基于模型的方法、数据驱动方法和融合方法。基于模型的方法主要从电池的物理机理出发进行建模和探究，电池的SOH受温度、充放电电流、工况条件、放电深度等众多因素的综合影响，各因素相互耦合，其机理较复杂，文献[1]建立了铅酸电池的二阶等效电路模型，并利用迭代递推最小二乘法对模型中的参数进行辨识，但该模型较简化，没有考虑更为复杂和实际的工况，无法刻画电池复杂的电化学反应。文献[2]在此基础上，结合电气和电化学知识，将电池分为放电初期、稳定放电阶段以及充电阶段，提高了模型的准确率。但总的来说，基于物理模型的方法存在机理不明晰、建模困难的问题，现阶段无法准确刻画电池内部各要素的具体作用和耦合关系，因此造成模型的局限性较大，实际应用价值不高。

与此同时，基于数据驱动的方法发挥了较大的作用，该方法无需考虑电池的复杂电化学机理，属于机器学习的范畴，通过对已知样本进行学习，来辨识和掌握所考察对象的数据特征，当有新的样本输入时，就可以据此进行预测，该方法的适应性较强，随着研究目标的改变，能够灵活地调整训练对象，建立新的预测模型。文献[3]采用支持向量机（support vector machine，SVM），建立了反映蓄电池端电压、内阻和SOC的预测回归模型。文献[4]采用相关向量机（relevance vector machine，RVM）的方法，只保留迭代过程中的非零向量，因而相比支持向量机，减少了计算量。文献[5]采用BP神经网络，以电池端电压和充放电电流采集值为输入，SOC为输出，建立神经网络模型，并采用梯度下降法训练模型的权重和偏值。文献[6]采用模糊神经网络（fuzzy neural network，FNN），用粒子群算法对模型中的权重、偏值和隶属度函数进行优化。总的来说，基于神经网络的预测方法需要大量的训练数据，回归模型的准备时间较长。

混合方法将基于数据驱动的方法和基于模型的方法相融合，试图克服数据驱动方法对于数据量的依赖性和基于模型的方法中由于模型本身的误差而导致对于客观物理对象描述的不准确性，比如用数据驱动的方法来获取机理模型中测量方程的输出值，以减少在复杂工况下，模型参数辨识不准确导致的估计误差。文献[7]用DS（dempster-shafer）理论来初始化训练数据集，并用蒙特卡洛方法来更新电池容量退化双指数模型中的参数。文献[8]用卡尔曼滤波算法（KF）来增强电池容量的相关向量机模型，提高了预测的长期性和预测精度。文献[9]用离线的电池模型参数作为容量退化的特征量，来训练灰色神经网络模型，并用于在线容量估计。这类方法的鲁棒性较好，具有较强的参数修正能力，但总的来说，混合方法提高了预测模型和估计算法的复杂度，在提高可靠性的同时不可避免地导致预测精度的降低。

高斯过程回归（Gaussian process regression，GPR）[10]是最近发展起来的一种基于贝叶斯框架的回归方法，在处理高维度、小样本、强非线性的问题中具有较强优势，适合电池这一强非线性系统。本文首先提取铅酸蓄电池的充电特征曲线，分析对比了恒流充电阶段的相关特征。然后建立起GPR模型，采用混沌粒子群算法（CPSO）对模型中的超参数进行优化，找到高质量的超参数。两种算法相互协同，形成了CPSO-GPR算法，实验结果表明，用该算法来预测新样本点的SOH值，估计精度在3%以内。

1 恒流充电特征分析对比

铅酸蓄电池属于二次电池，其具有可逆的化学反应，即“双硫酸盐化反应”，在正负级都会有PbSO4生成。充电过程是正、负极板上的PbSO4得电子，和水反应，分别在正、负极生成PbO2和Pb。放电反应是正、负极的活性物质分别与电解液H2SO4反应，失电子生成 PbSO4，随着PbSO4扩散到正、负极的活性物质里面，使得H2SO4难以入内参与化学反应，使得放电电压急剧下降。铅酸蓄电池可以反复充、放电多次，每次体系恢复到原始状态，但由于极板老化、硫酸盐化和板栅腐蚀等原因，电池的可用容量逐渐衰减。

下面用循环充、放电实验来获取铅酸电池的容量衰减曲线。充电实验采用先恒流充电再恒压充电[4]的形式，这种方法较温和，对电池的冲击较小，且保证较高的充电效率。放电实验则采用恒流放电。

电池参数为：额定容量200 A·h，循环充电电压（14.70±0.18）V，最大充电电流50 A。

实验步骤为：1）20 A恒流充电；2）当端电压达到14.4 V时，转为恒压充电，当充电电流下降到2.4 A时，充电阶段结束；3）40 A恒流放电，同时用传感器记录放电电流和时间，用A·h计量法计算实际容量；4）端电压达到截止电压1.6 V时，一个充、放电循环结束；5）重复1）～4）步骤52次。得到容量随循环次数的变化曲线如图1所示。

图1 电池容量退化趋势Fig.1 The degeneration trend of battery capacity

记录每次循环充放电过程中的恒流充电时间和恒压充电时间随当前容量的对应关系，得到如图2所示的关系曲线。由图2易知，恒压、恒流充电阶段时间和充电总时间随容量衰减而变化显著。设充电总时间、恒压和恒流充电时间分别为T，T1，T2，分别计算灰色关联度和皮尔逊相关系数来选取相关性最高的量，得到表1。

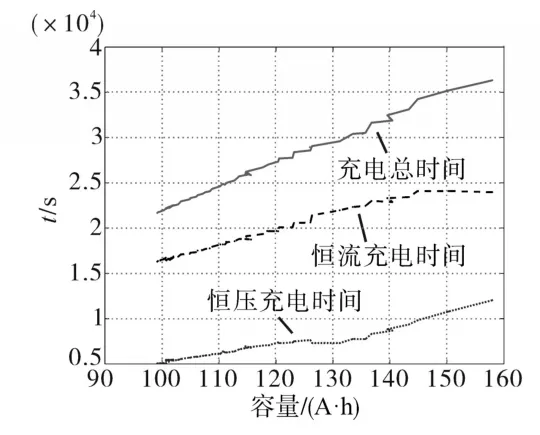
图2 电池容量和充电时间的关系曲线Fig.2 Relevance curves between battery capacity and charging time

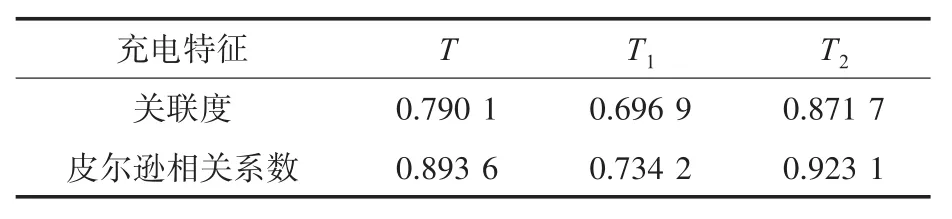
表1 灰色关联度分析结果Tab.1 Results of grey relevance analysis

故选取恒流充电时间T2序列和电池循环容量序列，建立GPR模型。

2 铅酸蓄电池高斯过程回归模型的建立

高斯过程又名正态随机过程，面对小样本、高维度和强非线性的样本时具有较好的学习能力[8]。

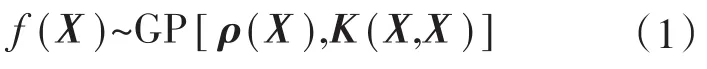
式中：K（X，X）为训练样本X的协方差矩阵；ρ（X）为训练样本X的均值矩阵。

可建立如下的高斯过程模型：

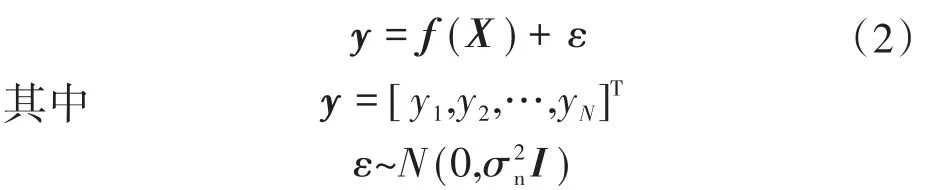
式中：y为输出向量为高斯白噪声；I为单位矩阵为方差。

由于白噪声相互独立，则y也属于高斯过程，由贝叶斯原理可知，y的先验分布为

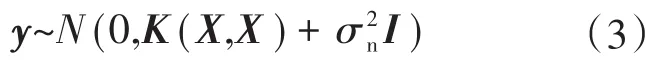
对于一组新的样本(x*,y*)，可知目标输出向量y和测试样本的输出y*符合联合高斯分布，即

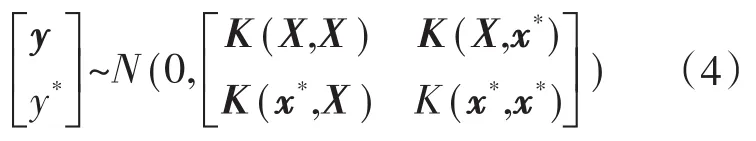
K矩阵的第i行第j列元素Kij=k(xi,xj)为核函数。由贝叶斯后验分布公式可知：

易知y*的置信度为0.997 3的置信区间为核函数取平方指数核函数[9]，用输入变量之间的距离来反映相关性，即

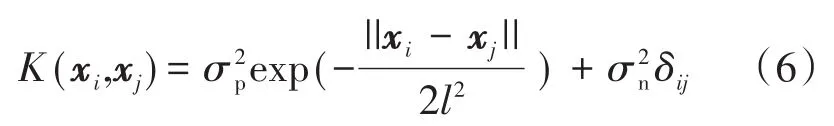
式中：σp为核函数标准差，描述输入变量的局部相关性；l为带宽，控制核函数的光滑程度。

σp，l，σn为超参数；当i=j时，控制系数δij=1，否则为0。

GPR的缺点在于回归模型中的超参数过多，选取不当会直接影响模型的回归性能。超参数寻优的本质是最小化训练样本的预测值和真实值之间的均方误差，是一类无约束优化问题，即

式中：m为验证集的个数。

式（7）的解析复杂，求导困难，超参数的初值难以估计，常用启发式算法进行优化，即初始化一个群，通过逐代进化，优胜劣汰，进而寻找到一个高质量的解。

3 混沌粒子群算法

粒子群算法[11]是一种优秀的启发式算法，其参数较少，收敛速度快，全局性能好，而且不需要提供目标函数的导数信息，适合用于参数辨识、超参数优化等领域。传统的粒子群算法容易陷入局部最优解[10-11]而导致解的质量不高。本文将混沌过程引入PSO中，形成了混沌粒子群算法，以提高其寻优的广度和深度，获取更高质量的超参数解，提升GPR模型的回归预测效果。

3.1 混沌初始化

混沌具有遍历性，有助于产生尽可能覆盖可行区域的初始粒子。这里采用logistic序列[12]Ui+1=μUi（1-Ui）来初始化种群。当μ=4时达到完全混沌状态。先产生n维混沌变量U0（n为超参数个数），代入logistic序列中迭代M次（M＞m，m为粒子总数），生成M个混沌向量，逐一反映射到自变量的取值区间，生成M个粒子。第i个粒子Ui=（δip，li，δin），包含了 GPR可能的超参数信息。将每个粒子带入到式（7）中，比较目标函数值，选取最优的m个粒子作为初始种群。较优的初始种群能够避免低效率搜索，加速寻优进程。

3.2 混沌搜索

常规PSO中粒子速度和位置的迭代公式如下：

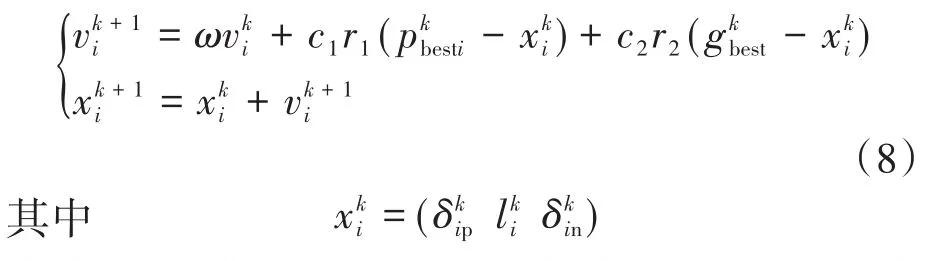
式中：ω为惯性因子；c1，c2为学习因子；r1，r2为(0,1)之间的随机数为粒子i在第k次迭代时的位置为粒子i在第k次迭代时的速度为粒子i的历史最优位置是当前全局最优位置。

为了提高寻优的广度，在粒子运动过程中加入混沌搜索。粒子的速度位置在第k次更新时，采用如下方法：随机产生n维向量uo，uoi∈(0,1)。代入logistic方程迭代T次，生成T个混沌向量ut,t=1,2,…,T。令控制混沌搜索的幅度，取为摄动步长，代入式（8）中，迭代更新公式化为

此时粒子i有T个混沌速度位置1,2,…,T和1个不加混沌摄动的速度位置对这T+1种选择，取最优结果作为第k+1迭代时的速度和位置，即

将式（10）代入式（9）中重复进行。

3.3 交叉变异操作

遗传算法[13]（genetic algorithm，GA）的交叉变异操作有助于算法跳出局部最优解，借鉴这一思想，当种群的平均适应度变化较小时，对种群进行交叉和变异操作，有助于获取新个体，将种群引入新的搜索区域。

采用多项式交叉。对粒子i和j交叉操作后产生的两个个体为

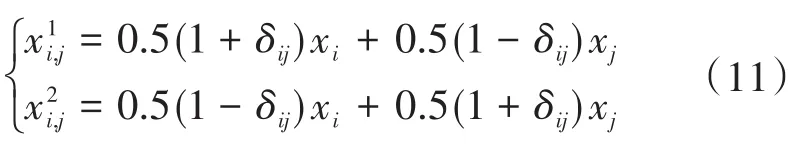
其中

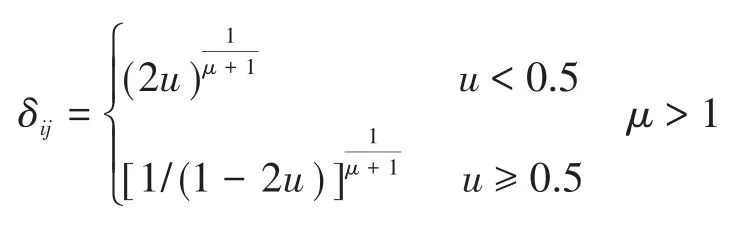
式中：δij为交叉因子；u为（0，1）之间的随机数。

对于粒子i，定义变异因子：

变异后新粒子为

4 CPSO-GPR算法的基本步骤

将样本集合D随机划分为k个互斥子集[9]，即D=D1∪D2∪…∪Dk,Di∩Dj=∅，依次选取Di，i=1，2，…，k为验证集，其余子集为训练集。代入式（8）中，并用混沌粒子群算法优化问题，以获取高质量的超参数解，经过k轮验证后，选取最优的结果（验证集中y的真实值和预测值的均方误差最小）作为模型的超参数解，建立GPR回归模型，用于新的数据点的预测，并可给出置信区间。CPSO-GPR算法的基本流程图如图3所示，其中，fav为粒子的平均适应度，s为迭代计数变量。

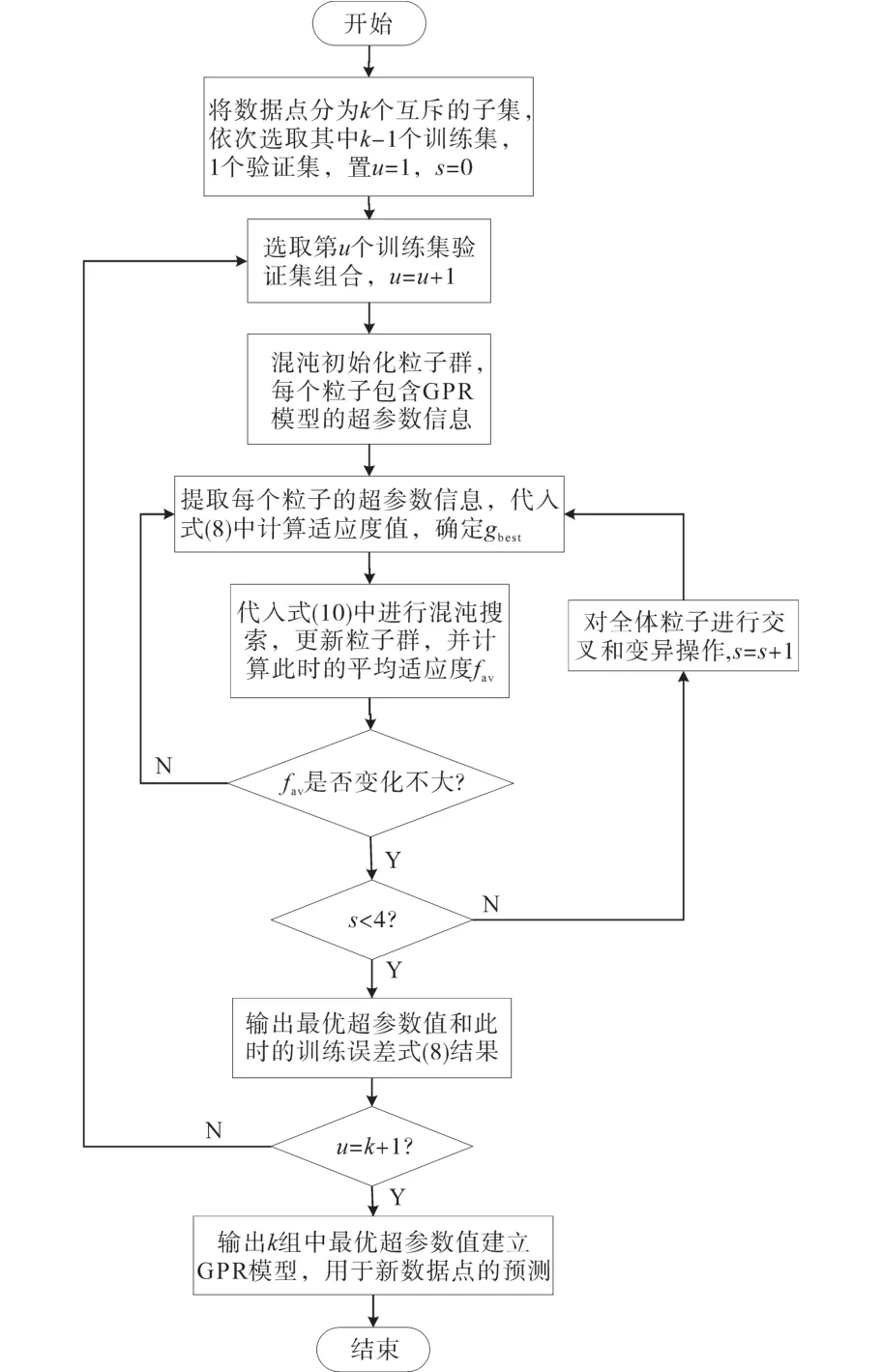
图3 CPSO-GPR算法流程图Fig.3 The flow chart of CPSO-GPR

5 实验验证与结论

将铅酸蓄电池52个充、放电循环的恒流充电时间数据集的前26个数据点作为训练数据，后26个数据点作为测试数据，来预测SOH值。训练数据和测试数据都为2×1维的矩阵，第1行为恒流充电时间，第2行为相应的当前可用容量。实验过程和实验数据的具体细节参见文献[4]。训练数据随机划分为两个互斥子集，其中一个为训练集，另一个为验证集，用于建立GPR模型。

两个验证集的数据点预测结果和相对误差百分比如图4所示。可知，各交叉检验集的估计误差大多在1%以下，体现了较好的回归预测效果。

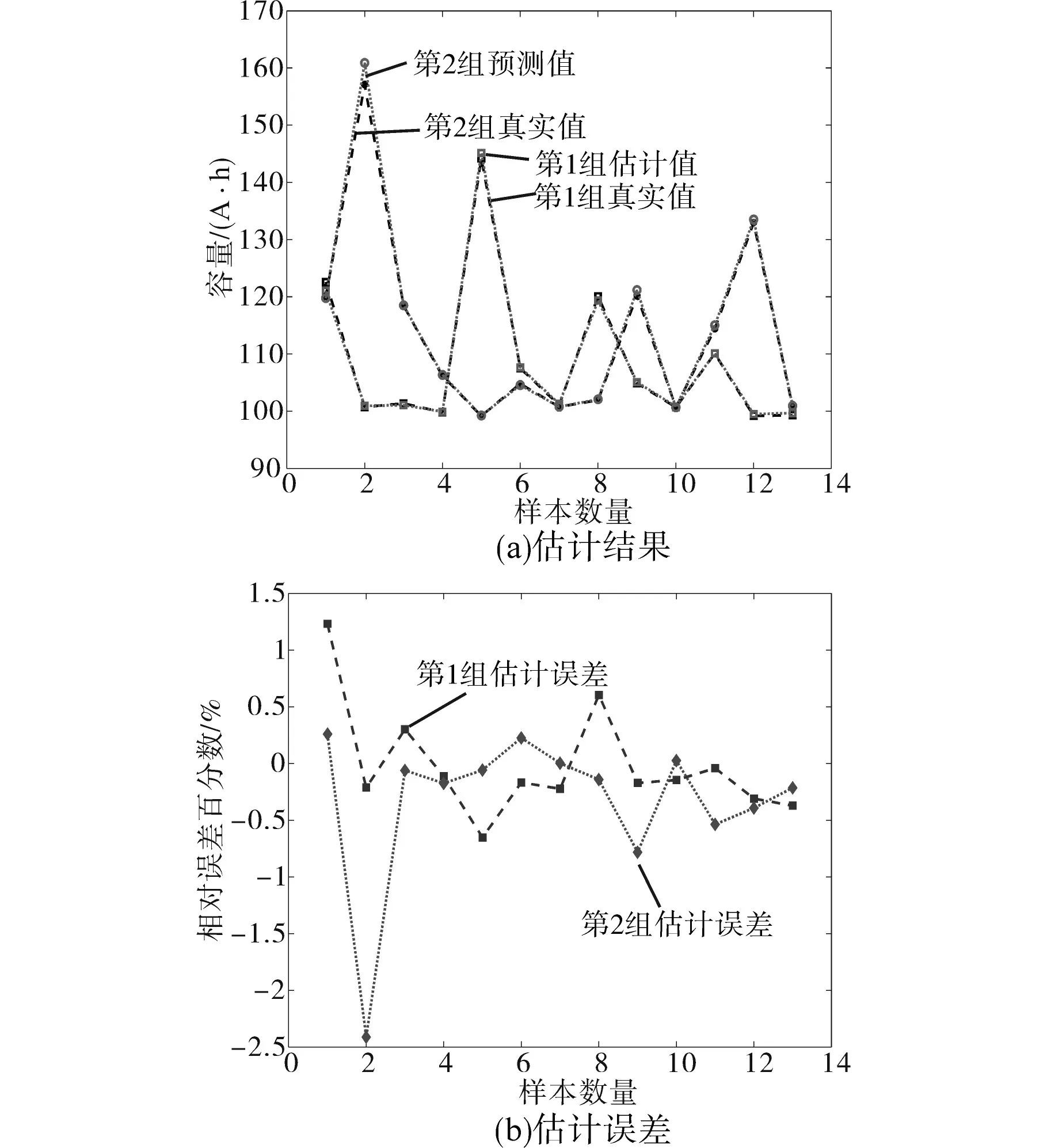
图4 估计结果及误差Fig.4 The estimation results and errors

为展示混沌粒子群[14]的优化效果，用常规粒子群算法优化问题（式（8）），并与CPSO做对比，得到图5，适应度函数选取式（7）。由图5可知，将混沌过程加入到粒子群算法中，增大了寻优的广度和深度，更加不容易陷入局部最优解，从而求得更小的拟合误差和更高质量的超参数值，提高了GPR模型的回归性能。

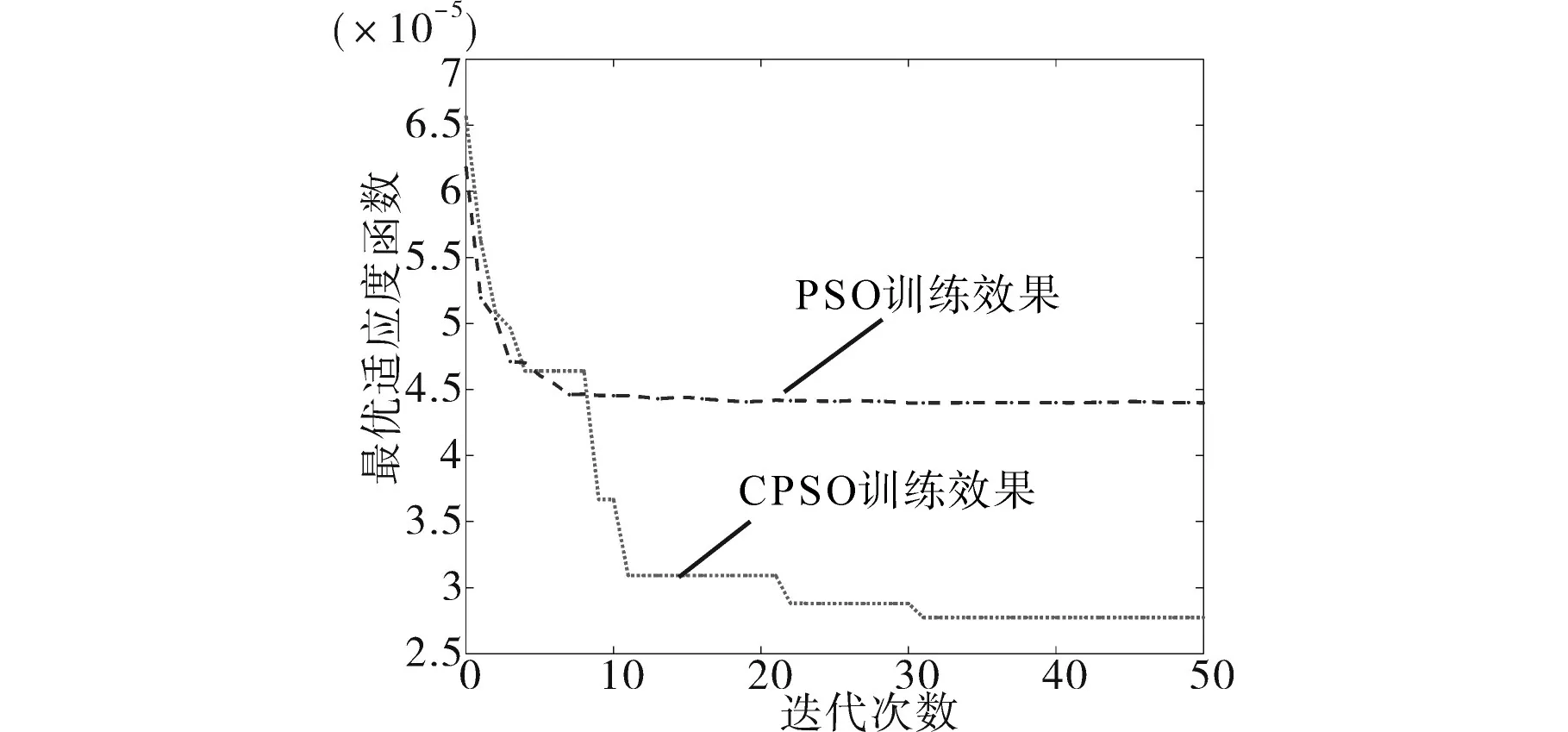
图5 CPSO和PSO优化效果对比Fig.5 The optimization effect of CPSO and PSO

将新数据点，即后26个循环周期的恒流充电数据代入建立好的GPR模型中，给出预测值和置信区间，如图6所示。由图6可知，99.5%的置信区间窄，表现出较好的预测性能。

图6 新数据点的预测值及其置信区间Fig.6 Prediction value and confidence interval of new data points

每个数据点的估计值与真实值的相对误差百分比如图7所示，可知最大误差百分比低于3%，精确度较高。

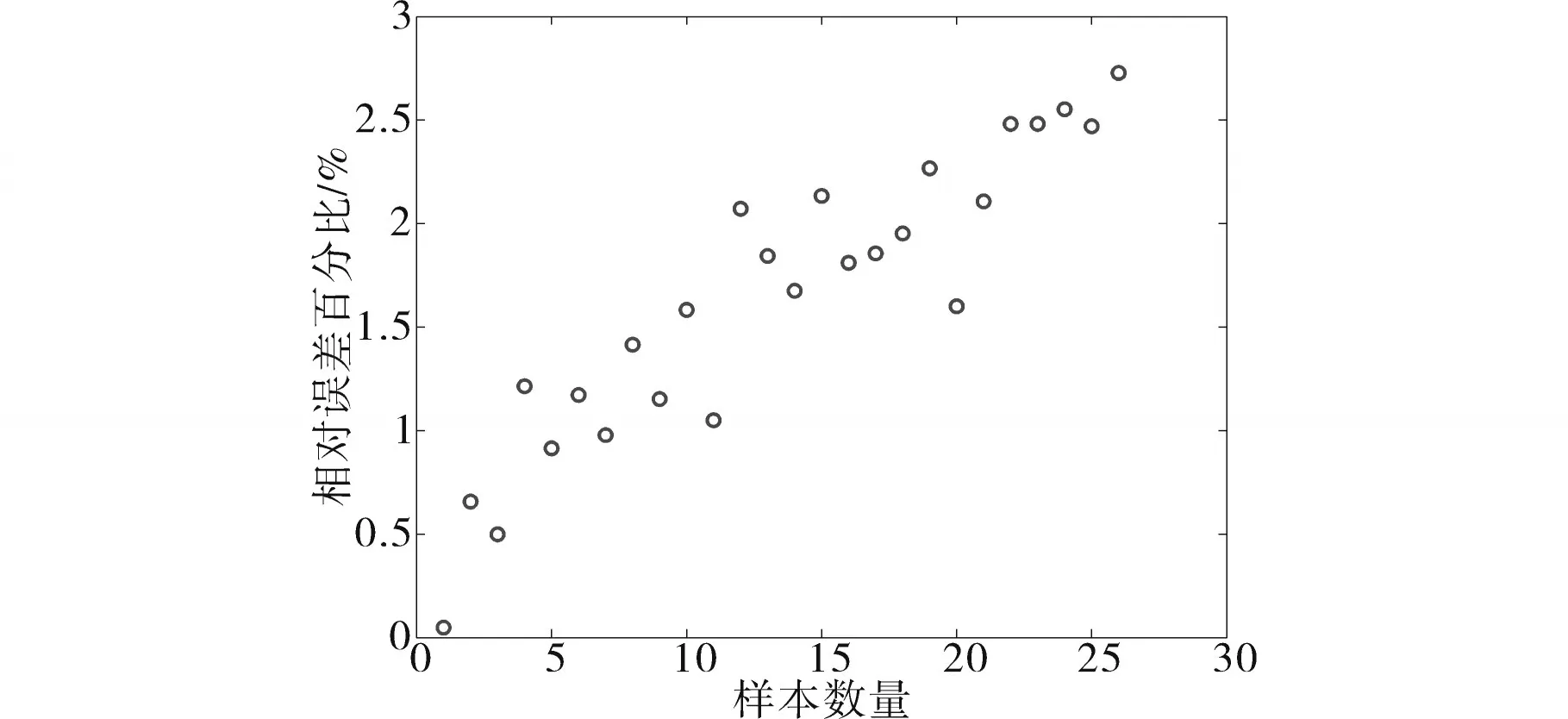
图7 新数据点的估计误差Fig.7 Estimation error of new data points

本文提出了CPSO-GPR算法用于铅酸蓄电池的SOH估计中。首先提取铅酸电池充电阶段的健康特征，用恒流充电时间作为表征电池当前SOH值的重要指标。将混沌过程引入到粒子群算法中，以增强其寻优的广度和深度，用CPSO算法优化高斯过程回归模型中的超参数，即最小化验证集预测值与真实值之间的均方误差。获取最优的超参数解以后，用新的数据点进行预测，估计误差在3%以内。结果表明，CPSO算法有助于提升GPR的回归性能，进而实现对铅酸蓄电池健康状态的精准估计，此外，由图5可知，CPSO算法收敛速度较快，在进行到30代左右就可以获取较高质量的超参数解，CPSO-GPR的运算时间在5 s以内，具有实时性，适合于电池SOH的在线检测。