基于置信度的飞行时间点云去噪方法

王明星，郑 福，王艳秋，孙志斌

基于置信度的飞行时间点云去噪方法

王明星1,2，郑 福1，王艳秋1,2，孙志斌1,2

（1. 中国科学院国家空间科学中心，北京 100190；2. 中国科学院大学，北京 100049）

飞行时间（Time-of-Flight，ToF）三维成像方法由于多路径干扰和混合像素等问题降低了目标物体深度测量的精度。传统的方法通过优化重构异常点云数据或滤除噪声点云数据来提高目标的准确性，但是这些方法复杂度高且容易导致过度平滑。三维点云图像中的有效点云与噪声点云之间的关系很难用数学模型来表示。针对上述问题，本文提出了一种基于置信度的飞行时间点云去噪方法。首先，分析多帧点云数据的概率相关性，以点云数据的置信度作为判别有效点云与噪声点云的依据；其次，利用多帧点云之间的矢量对偶性，提出了一种快速提取不同置信度点云的算法，其时间复杂度为()；最后使用该算法提取多帧三维图像中置信度高的点云数据获得目标物体的真实测量数据，并重点对4组不同场景的点云数据进行对比实验。实验结果表明，该算法能够在有效滤除噪声的同时，显著提高目标物体的距离测量精度，增强目标物体的特征，因此具有广泛的应用价值。

飞行时间；点云去噪；置信度

0 引言

近20年以来，飞行时间三维成像方法因具有非接触测量、响应速度快等优势，在工业生产、科学研究、计算机视觉、自主导航等领域得到广泛的应用。飞行时间三维成像方法是通过向目标物体发射近红外强度调制信号，传感器接收从目标物体返回的调制信号，然后对发射信号与接收信号进行相位解调获得目标物体与飞行时间相关的相位差数据，最后计算获得目标物体的距离信息[1]。在实际应用中，存在系统相关噪声和非相关噪声，其中系统噪声包括深度畸变噪声、积分时间相关噪声、像素相关噪声、振幅相关噪声和温度相关噪声[2]；非相关噪声是指多径干扰[3]、背景光产生的噪声等。

现有的点云去噪方法主要可以分为4类：基于移动最小二乘（moving least squares，MLS）的方法、基于局部最优投影（locally optimal projection，LOP）的方法、基于稀疏性的方法和非局部的方法[4]。

基于移动最小二乘的方法首先根据最小二乘法确定每个点的局部参考域，然后拟合一个基于参考域的多项式函数，最终将输入点云拟合出一个平滑曲面，并将点投影到生成的曲面上[5]。文献[6]提出代数点集曲面（algebraic point set surfaces，APSS）的方法，利用局部移动最小二乘法拟合代数球面，通过控制拟合球面的曲率，解决了高曲率情况下不稳定重构的问题。文献[7]提出一种鲁棒的隐式最小二乘法（robust implicit MLS，RIMLS），解决了移动最小二乘法对异常值和尖锐特征敏感的问题。然而，这些方法存在过度平滑的问题[8]。

基于局部最优投影的方法与基于MLS的方法不同，它不计算曲面的显式参数。文献[9]中通过最小化到数据点的欧氏距离之和来定义表示估计曲面的一组点。它的两个改进版本是加权局部最优投影（weighted LOP, WLOP）[10]和边缘感知点集重采样（edge-aware resampling，EAR）[11]。WLOP通过使排斥项适应局部密度来输出分布更均匀的点云，而EAR通过局部各向异性投影进行重采样来保留尖锐特征。然而，基于局部最优投影的方法也存在过度平滑的问题[8]。

基于稀疏性的方法假设每个局部是平面，并针对某些几何特征的稀疏表示进行优化。基于表面法线稀疏性的方法首先通过使用L0[8]或L1[12]正则化求解全局极小化问题得到表面法线的稀疏重建，然后基于局部平面假设解决另一个全局极小化问题来使用表面法线更新点的位置。但是，在局部噪声比较高的情况下，法线估计会产生较大的误差，由此导致过度平滑或过度锐化[8]。

非局部的方法将数字图像去噪算法中非局部均值（non-local means，NLM）[13]和三维块匹配滤波（block-matching and 3D filtering，BM3D）[14]的非局部自相似性概念应用到点云去噪中，在高噪声水平下能够更好地保留结构特征。文献[15]中利用基于曲率的相似性进行非局部滤波，由于滤波过程中考虑了邻域的几何结构，更好地保留了精细的形状特征。然而，这些方法的计算复杂度很高。

综述分析了各类点云去噪方法，本文提出的基于置信度的点云去噪算法不属于上述中的任何一类。它跳出了从单帧点云分析的思维局限，利用统计学的方法分析多帧有序点云，计算点云的置信度，如果该点云的置信度大于给定的置信度阈值，则该点为有效点，予以保留；相反，若小于给定的置信度阈值，则该点为噪声点，予以删除。

1 飞行时间三维成像原理与噪声分析

飞行时间三维成像设备主要包括发射端和接收端，如图1所示，控制器发送调制信号到激光器，控制激光器发出调制的近红外光，经过物体漫反射后，接收端传感器接收反射回来的调制光，最后根据发射信号与接收信号的相位差来计算深度信息。相位差D是由4个不同相位延迟的接收窗口的电荷量1、2、3、4计算得到[1]：

获得相位差之后，根据公式(2)计算目标物体与相机之间的距离：

式中：表示光速；表示发射信号的调制频率。

图1 TOF相机成像原理

公式(2)中，相位差D的取值范围为[0, 2p]，因此相机能测量的最大距离为/2，与调制频率成反比，频率越低，能够测量的范围就越大，但是随之带来的是测量精度的下降。若目标超过相机能够测量的最大距离，测量得到的错误值依然落在[0,/2]区间内，这种噪声混杂在真实点云中难以滤除。因而在实际应用中，面对不同距离的测量场景，需要调制不同频率的发射信号。

在飞行时间相机获取的点云图中，物体与背景之间以及物体边缘处存在大量的飞行像素噪声（flying pixels[16]），这是由于目标物体测量的距离信息和背景测量的距离信息混合后产生的干扰噪声。当飞行时间相机的单个传感单元同时接收到前景和背景反射回来的调制光[17]，如图2所示，二者产生的能量叠加在一起，使用公式(1)计算得到错误的相位差，此时传感器测量得到的距离介于前景与背景之间，导致生成3D点云后，出现了实际场景中不存在的飞行像素噪声。尤其在拍摄对象细节丰富的情况下，飞行像素噪声散落在物体边缘，如图3(a)所示，在视觉上物体的边缘信息已经完全被破坏。因此在进行点云分割、配准、重建等下游任务之前必须有效去除噪声。

另外，如图3(b)中椭圆标记2，在相机镜头与目标之间存在实际场景中不存在的噪声，这是由于场景中的镜面反射引起的。同时，反射率不合适的目标材料、镜头散射以及多径干扰也是噪声产生的原因[16-17]。

图2 飞行像素噪声的产生

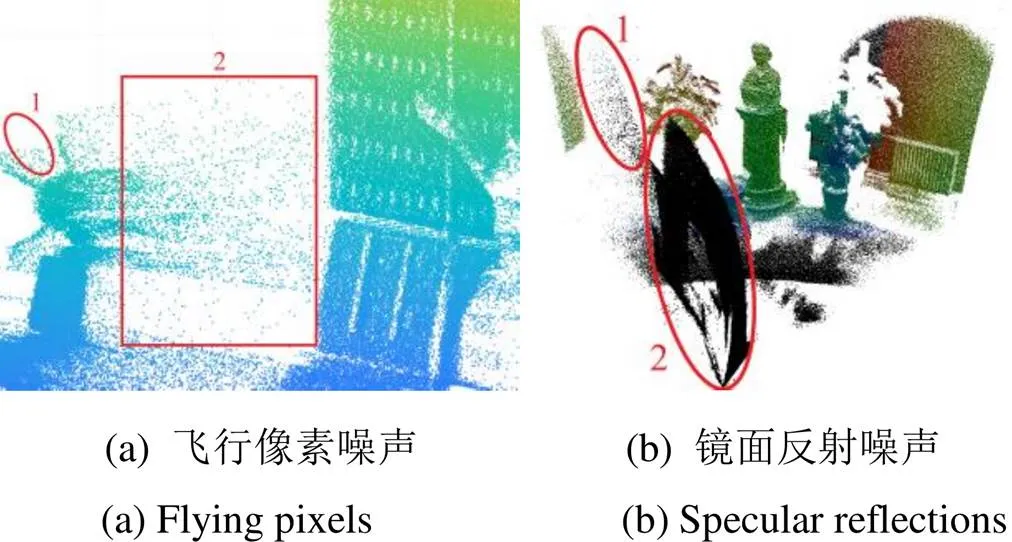
图3 实际场景中点云噪声示例

2 点云置信度的定义

由于存在噪声，传感器的各个传感单元获取的点云数据存在误差或者缺失的现象。具体表现为：本该接收到红外反射光的图像传感单元，由于太阳反射光直流分量或是硬件问题导致红外反射光丢失，呈现点云缺失的现象；一些本不应该接收到反射光的图像传感单元，受物体漫反射、多路径干扰等影响接收到距离信息，产生飞行像素噪声。对此本文利用有效点云与噪声之间的非相关性，定义了点云置信度的概念。当把图像传感单元采集的数据作为一个随机变量，点云噪声以较低的概率被图像传感单元接收，而有效点云以较高概率被采集。对同一个目标进行多次测量，根据图像传感单元采集的次数计算置信度。

本实验采用的飞行时间传感器有307200个图像传感单元对目标进行测量，并输出有序点云数据。当对同一目标采集次，则第个图像传感单元采集的点云的置信度为：

即按采集次数计算点云的置信度，当采集10幅图时将会有10组点云，若10次图像传感单元都接收到了信息，计算该点云置信度为100%，可以认为该图像传感器单元接收到的是有效的信息。若10次测量中只有1次采集到信息时，计算该点云置信度为10%，那么可以认为该图像传感单元接收到的是噪声。

3 基于置信度的点云去噪算法

根据公式(3)可以求出各个传感单元获取的点云的置信度，若直接对幅点云图像遍历求得t，在面对数据量极大的点云时，其复杂度相对较高。本文提出了一种通过矢量对偶点云加和的方式快速提取不同置信度的点云方法，该方法能够以很小的时间和空间复杂度提取出符合置信度要求的点云。当使用飞行时间传感器采集到副点云图时，对其中第幅图像的传感单元进行研究，若传感单元接收到物体反射信号，该传感单元将会根据公式(1)和(2)计算输出该点云的三维坐标L＝(X,Y, Z)，若传感单元没有接收到物体反射信号，该传感单元会输出一个极大的偏置L＝max＝(max,max,max)，表明该点区域没有物体，即该点为无效点。若在次采集中图像传感器单元只有次采集到数据，对该传感单元次获取的三维坐标进行求和有：

式中：sum,j是图像传感单元采集次的三维坐标之和，由于被正确采集时，三维坐标数据受随机误差影响在小数量级浮动，可以近似表示为sum,j＝*1j；当只有次被采集时，同理sum,j可以近似表示为sum,j＝*L＋(－)*max。这样根据未被采集的次数－，sum,j就会相对于原始点云进行(－)*max的偏移，因此只要偏置max足够大时，对这些点云进行直通滤波处理，就可以很容易提取出不同置信度的点云。

基于置信度的点云去噪算法的伪代码如下所示：

算法基于置信度的点云去噪 输入: //n帧点云图像 输出: //点云集和对应置信度 1：if//检查是否为同源点云 2： //矢量加和 3： //分割提取 4： 5：else 6： output输入错误 7： return 8：return

基于置信度的点云去噪算法的计算主要集中在点云坐标的相加，时间复杂度为()，是常量，取决于点云图的分辨率以及帧数。一般来说，对于常量级的加法操作，其复杂度几乎可以忽略不计。

4 实验与分析

4.1 飞行时间点云获取和预处理

以实验中一组数据为例，首先将“东方红一号”1:15的模型固定在光学实验平台中央，然后利用飞行时间传感器从4个不同的角度分别采集10帧数据，4个角度之间相隔90°左右。实验装置如图4所示。

实验获取的点云数据如图5所示，点云数据中包含了大量与目标物体无关的背景数据以及噪点，并且由于物体的遮挡，如图5(a)、(c)所示，在目标物体和背景之间存在大量的飞行像素噪声。对原始数据进行直通滤波实现目标提取，目标提取结果如图5(b)、(c)所示，目标物体背面的点云比较稀疏和散乱，给后续的点云拼接与重建工作带来了较大阻碍。

图4 实验装置

图5 TOF相机拍摄的点云数据示例

4.2 基于置信度的点云去噪

本文实验使用的传感器分辨率为480×640，输出有序点云数据。实验在固定位置对目标连续采集10帧图像。将每一个图像传感器单元采集到的10个三维坐标进行求和，得到的点云如图6所示，从左上角到右下角很明显地分成了10个区域，由于这10个区域在空间中是彼此分离的，因此很容易分别提取出来。左上角为10帧图像中采集到10次的点，在这10帧图像中它的置信度为100%，右下角为10帧图像只采集到一次的点，它的置信度为10%。

图6 10帧点云图各像素单元求和结果

将图6中不同置信度的点云分别提取出来，得到的结果如图7所示。其中100%置信度的点云具有最丰富的细节，表面特征相较于原始点云更加明显，这是因为这些点被百分之百接收。另外，其它置信度的点云基本上都分布在目标物体的边缘，说明物体的边缘比较容易产生异常点和噪声，这与飞行像素噪声产生的原理是相吻合的。

表1统计了不同置信度的点云数量及其所占比率，其中100%置信度的点云所占比率为0.9425，这表明基于置信度的点云去噪方法能够保证在有效数据不损失的前提下去除噪声。另外，根据需求降低置信度阈值可以丰富目标边缘信息。

图7 提取不同置信度点云结果

表1 不同置信度的点云数量及所占比率

图8（左）是置信度为100%的点云数据，与图5中的(b)、(d)比较，置信度去噪后的点云相比于原始的点云以及经过统计滤波的点云有明显的提升：

1）传统的滤波方法无法对混杂在正确点云中的噪声进行滤除，而基于置信度的点云去噪方法能找到置信度不高的点云进行滤除，并且具有复杂度低、效率高的优点。

2）提高测量精度。基于置信度点云去噪的结果中点云分布相较原始点云更加细致有序。由于随机误差、计算精度等，测量得到的点云三维坐标存在随机误差的情况，假设该误差以高斯分布形式出现(,2)，当利用10幅图进行置信度去噪后，根据统计学原理，该点的分布会变成(, 0.1*2)，即对点云进行了校正。实验中选取图8（左）红色框选区域的点云数据，其坐标范围为[4,15]，坐标范围为[13,14]，分析在置信度去噪前后的距离随坐标变化的图像，其分布如图8（右）所示，原始图像距离的范围为[362.75, 376.75]，置信度去噪后的距离的范围为[365, 370.23]，即原始图像的距离测量精度为±7.00mm，置信度去噪后的距离测量精度为±2.62mm，精度提高了62.86%。

图8 置信度去噪结果(左）和红色选中区域置信度去噪前后距离Z随坐标X的变化图像（右）

3）增强目标物体特征。传统滤波根据点云的空间分布信息进行滤波，使得一些零散却有效的点被滤除，表现为特征模糊。而基于置信度的点云去噪能保留这些特征，如图8（左）所示，卫星模型的表面结构更加清晰，有利于后续配准、重建等工作。

边缘缺失的点云是卫星模型72面球体结构的特殊性造成的。缺失部分对应的镜面反射路径朝着远离相机传感器的方向，传感器无法接收该部分反射光信息，导致点云缺失。缺失部分可以采用多视角点云配准的方式进行补全，最终实现完整的三维重建。

4.3 不同帧数的置信度去噪对比实验

实验按照目标物体的类型分为A、B、C、D四组。分别测试利用不同帧数的去噪效果，并与直通滤波方法进行对比。

其中A1、A2是在室内用飞行时间传感器从2个不同的角度获取的“东方红一号”1:15的模型拍摄的点云数据。B1、B2是在室外用飞行时间传感器从2个不同的角度获取的汽车的点云数据。C1、C2是在室内用飞行时间传感器从2个不同的角度获取的雕塑的点云数据。D1、D2是在室内用飞行时间传感器从2个不同的角度获取的木制椅子的点云数据。

实验中对各组数据分别进行直通滤波以及2帧、4帧、6帧、8帧、10帧的置信度去噪处理。表2显示了不同帧数置信度去噪后点云的数量，可以看出A、B两组点云数量随着帧数的增加呈现的下降趋势比C、D两组更加明显，这是因为A、B组的目标物体表面为金属材质，高反光条件下获取的数据中的噪声相对更多。

实验发现，通过2帧点云数据的置信度去噪，能够达到较好的去噪效果，在有效滤除噪声的同时能够保留目标物体的特征。如图9所示，相比于原图，在两帧点云加和后，点云图中的目标物体周围的飞行像素噪声几乎消失了，目标提取变得更加容易，为后续的配准以及重建工作创造了有利条件。

图10列出了A1、B1、C1、D1组在不同帧数加和的效果以及对应置信度去噪的结果。点云帧数越多，置信度去噪后点云数量越少，例如，在B1组数据的置信度去噪结果中，车顶部分的点云随帧数增加变得稀疏。在C1、D1组中，由于获取的原始点云目标物体周围噪声相对较少，10帧点云的置信度去噪与2帧点云的置信度去噪结果从视觉上不易发现差别，都完整地保留了目标物体的特征。这也说明了本文算法去除点云噪声能力较强，而对于有效的目标点云能够较好地保留下来。

图9 B1组原始点云俯视图（左）与2帧加和后点云俯视图（右）对比

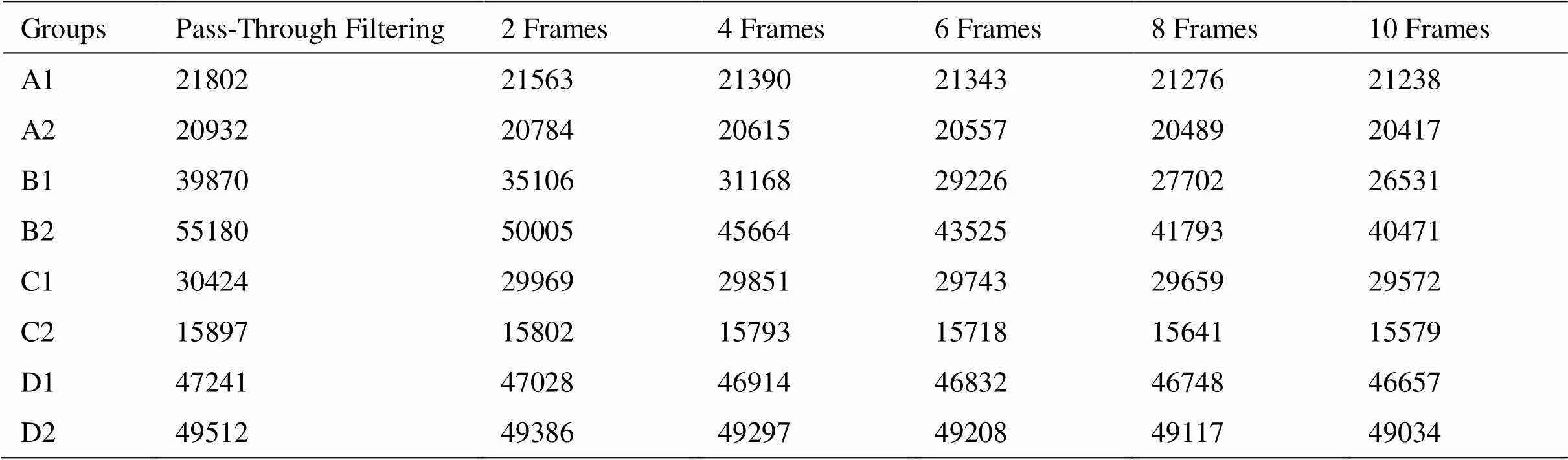
表2 不同帧数置信度去噪后点云数量

5 结论

本文提出了一种基于置信度的点云去噪方法，实验证明，它能够快速有效地去除ToF点云中的噪声，去除噪声占比达5.75%，还能减小随机误差，目标物体的距离测量精度提高了62.86%，同时增强目标物体的特征。这种方法对于通过其它方式获取的同源有序点云数据同样适用，具有可推广性。

本文算法简单高效，时间复杂度为()，点云帧数和置信度阈值在实验中需要根据实际情况进行选择，因此可以考虑直接将算法嵌入相机芯片或者集成到通用图像捕获软件中，把置信度作为一个设置参数，直接输出经过置信度去噪后的点云数据。在置信度较高时，目标物体的边缘若出现点云缺失的情况，可以通过多视角点云配准的方式进行补全。

[1] LI L. Time-of-flight camera–an introduction[R/OL]. [2021-10-08].chrome-extension://ibllepbpahcoppkjjllbabhnigcbffpi/http://www-cs.ccn y.cuny.edu/～ wolberg/capstone/kinect/ToFBasicsTI14.pdf.

[2] Foix S, Alenya G, Torras C. Lock-in time-of-flight (ToF) cameras: A survey[J]., 2011, 11(9): 1917-1926.

[3] Whyte R, Streeter L, Cree M J, et al. Review of methods for resolving multi-path interference in time-of-flight range cameras[C]//,, 2014: 629-632.

[4] ZENG J, CHEUNG G, Ng M, et al. 3D point cloud denoising using graph Laplacian regularization of a low dimensional manifold model[J]., 2019, 29: 3474-3489.

[5] Fleishman S, Cohen-Or D, Silva C T. Robust moving least-squares fitting with sharp features[J].(TOG), 2005, 24(3): 544-552.

[6] Guennebaud G, Germann M, Gross M. Dynamic sampling and rendering of algebraic point set surfaces[C]//, 2008, 27(2): 653-662.

[7] Öztireli A C, Guennebaud G, Gross M. Feature preserving point set surfaces based on non-linear kernel regression[C]//, 2009, 28(2): 493-501.

[8] SUN Y, Schaefer S, WANG W. Denoising point sets via L0 minimization[J]., 2015, 35: 2-15.

[9] Lipman Y, Cohen-Or D, Levin D, et al. Parameterization-free projection for geometry reconstruction[J].(TOG), 2007, 26(3): 22-es.

[10] HUANG H, LI D, ZHANG H, et al. Consolidation of unorganized point clouds for surface reconstruction[J].(TOG), 2009, 28(5): 1-7.

[11] HUANG H, WU S, GONG M, et al. Edge-aware point set resampling[J].(TOG), 2013, 32(1): 1-12.

[12] Avron H, Sharf A, Greif C, et al. ℓ1-sparse reconstruction of sharp point set surfaces[J].(TOG), 2010, 29(5): 1-12.

[13] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C]//(CVPR'05), 2005, 2: 60-65.

[14] Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]., 2007, 16(8): 2080-2095.

[15] WANG R, CHEN W, ZHANG S, et al. Similarity-based denoising of point-sampled surfaces[J]., 2008, 9(6): 807-815.

[16] HE Y, CHEN S. Recent advances in 3D data acquisition and processing by time-of-flight camera[J]., 2019, 7: 12495-12510.

[17] Reynolds M, Doboš J, Peel L, et al. Capturing time-of-flight data with confidence[C]//,, 2011: 945-952.

Time-of-Flight Point Cloud Denoising Method Based on Confidence Level

WANG Mingxing1,2，ZHENG Fu1，WANG Yanqiu1,2，SUN Zhibin1,2

(1.,,100190,;2.,100049,)

The time-of-flight (ToF) 3D imaging method suffers from reduced precision in the depth measurement of target objects because of multipath interference and mixed pixels. Traditional methods improve the accuracy of the measurement by optimizing and reconstructing abnormal point cloud data or filtering noisy point cloud data. However, these methods are complex and can easily lead to excessive smoothing. The relationship between a valid point cloud and noisy point cloud in a 3D point cloud image is difficult to express using a mathematical model. To address these problems, a point cloud denoising method based on the confidence level is proposed in this paper. First, the probability correlation of multi-frame point cloud data is analyzed, and the confidence level of the point cloud data is used as the basis to distinguish valid point clouds from noisy point clouds. Second, by utilizing the vector duality between multi-frame point clouds, a fast algorithm for extracting point clouds with different confidence levels is presented, and its time complexity is(). Finally, the algorithm is used to extract the point cloud data with a high confidence level in multi-frame 3D images to obtain the real measurement data of the target object. We focus on the comparative experiments of four groups of point cloud data in different scenes. The experimental results show that the algorithm can not only effectively filter the noise but also significantly improve the distance measurement accuracy of the target object and enhance the characteristics of the target object; therefore, it has extensive application value.

ToF, point cloud denoising, confidence level

TN391

A

1001-8891(2022)05-0513-08

2021-10-08；

2021-11-11.

王明星（1998-），男，江西人，硕士研究生，主要研究方向为点云数据处理与应用，E-mail: wangmingxing20@mails.ucas.ac.cn。

孙志斌（1978-），男，山西人，博士，研究员，博士生导师，主要研究方向为空间光子学、光子信息学、空间材料学和物理电子学。E-mail: zbsun@nssc.ac.cn。

国家重点研发计划（2016YFE0131500）；中国科学院青年创新促进会优秀会员项目（2013105，Y201728）；中国科学院科研仪器设备研制项目（YJKYYQ20190008）；发改委国家重大科技基础设施（2018YFA0404201，2018YFA0404202）；空间科学战略先导专项（XDA15016300）；国家重大科学仪器设备开发专项（2013YQ030595）；空间科学战略先导专项（XDA15013600）；国家自然科学基金委面上项目（61474123，61274024）。