基于全连接神经网络方法的日最高气温预报
赵琳娜 卢 姝 齐 丹 许东蓓 应 爽
1)(中国气象科学研究院, 北京 100081)2)(成都信息工程大学大气科学学院, 成都 610225)3)(中国气象局-中国地质大学(武汉)极端天气气候与水文地质灾害研究中心, 武汉 430074)4)(湖南省气象台, 长沙 410118)5)(国家气象中心, 北京 100081)6)(吉林省长春市气象台, 长春 130062)
引 言
最高气温客观预报是天气预报的一项重要内容,有重要的实际应用意义[1],如交通管控、天气预报、农业生产和环境监测等各方面[2-3]。受大气动力过程、物理过程和局地地形、地貌等复杂因子的影响,数值模式的近地面要素预报常存在偏差,特别是转折性天气发生时日最高气温预报与实际观测间误差更大[3],因此实现日最高气温预报的精细化和精准化仍面临挑战。传统数值模式预报误差订正方法可在一定程度上改善预报效果,但存在局限性,如普遍针对单一空间点进行建模[4-7],不但计算量大[8],而且无法考虑站点间气象要素的相互影响。近年高质量遥感数据、数值预报产品网格产品以及各种气象观测数据快速增长[9],传统方法已很难处理海量增长的数据。
目前,深度学习已开始在数值天气预报中发挥作用,体现在数据预处理、同化、后处理等多个方面[10-12]。对于数值预报进行误差订正(数值模式后处理),机器学习一般将这类任务描述为回归问题,选取与预报因子相关联的其他气象要素作为特征集,以观测值作为目标集,再应用与回归相关的机器学习算法进行模型训练和评估,达到对预报目标误差订正的目的[13-14]。深度学习处理大数据的优势越来越明显,不仅可针对单一站点或格点建模,还可以充分挖掘气象数据的时空关系[15-17],神经网络能够进行各特征间更为复杂关系的学习[18],因而深度学习也成为误差订正的有效手段[19-21]。
深度学习所选取特征的质量对于模型预报效果有重要影响,因此特征工程是建模中极为重要的步骤。谭江红等[22]在进行湖北地面气温预报订正试验时,主要选取影响局地气温变化的因子,如不同高度层的风场、相对湿度等作为决策树集成模型输入,最终该方法的预报准确率优于同类客观产品以及模式产品。Rasp等[20]指出将本地信息编码进神经网络对于温度概率预报尤为重要,而添加辅助变量在其他研究中也得到广泛应用。Cho等[23]采用多种机器学习方法对韩国首尔地区LDAPS(Local Data Assimilation and Prediction System)模型输出的最高和最低气温进行误差订正,在构建特征时融合LDAPS模型预测因子、观测变量以及纬度、经度、海拔、坡度和太阳辐射5个辅助变量,并验证辅助变量对于模型的影响,表明当研究范围为城市区域内的站点时,设置表征地形和位置的辅助变量不能改善模型预测结果。任萍等[24]考虑复杂地形对于数值预报的影响,在构建多模式时间滞后集成模型时增加地形因素,结果表明这种构建方式使订正模型的误差特征更稳定。此外,Zamani等[25]在建立伊朗德黑兰城市地区PM2.5预测模型时,综合考虑覆盖观测站点上的卫星和气象数据、PM2.5观测数据等,同时也在数据集中加入记录样本时间和地理信息的特征,如年份、季节和经纬度等。
此外,人工神经网络方法的有效性很大程度取决于网络体系结构以及超参数的选择,通常主要依赖建模者的经验以及不断的试错试验[26]。Tran等[27]将人工神经网络模型的可训练参数数量分别设定为49,113,169,353和1001,并令隐藏层层数分别为1,3和5,经过构造多个网络架构进行对比测试,结果进一步验证了当模型中参数数量过少或过多可能导致欠拟合或过拟合训练集。为了充分利用数值天气预报产品的空间信息,Veldkamp等[28]应用卷积神经网络识别空间风速信息获得荷兰地区48 h预报时效的风速概率预报。Yu等[29]建立基于门控循环单元层(GRU)、卷积层(CNN)以及全连接层的DGCnetwork神经网络架构以预测东海与黄海地区的海表温度,其中设置GRU层和CNN层目的是分别提取数据中时间和空间特征。
鉴于特征质量以及神经网络结构在深度学习建模中的重要性,本文以全连接神经网络(fully connected neural networks,FCNN)为基本神经网络框架,设计带嵌入层的全连接神经网络模型,以便使神经网络模型识别样本的空间信息、时间信息并处理多类别变量。利用欧洲中期天气预报中心(ECMWF)高分辨率确定性模式HRES预报产品和全国2238个站点观测数据,建立全国2238个站的日最高气温神经网络预报模型,实现改进HRES日最高气温预报的目的。同时,为综合考察神经网络模型中特征的重要性以及网络结构的有效性,拟对辅助变量、时间滞后变量以及嵌入层的重要性分别进行评估,以期为提高日最高气温精细化预报的准确率提供新的方法和途径。
1 数据和预处理
1.1 数 据
本文使用的观测数据来源于国家气象信息中心的国家级地面气象站基本气象要素日值数据集(V3.0)。预报数据为国家气象信息中心收集的欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)高分辨率模式(high resolution,HRES)预报产品,该产品起报时间为08:00和20:00(北京时,下同),预报时效0~72 h的模式输出间隔为3 h。地面预报场的水平分辨率为0.125°×0.125°,高空预报场的水平分辨率为0.25°×0.25°。
本文利用24 h HRES模式产品和相应的日最高气温观测值,构建24 h最高气温预报神经网络模型。研究所用数据集时间长度为2015年1月15日—2020年12月31日,其中训练集时间为2015年1月15日—2019年9月30日,共1720 d,验证集时间为2019年10月1日—12月31日,测试集时间为2020年1月1日—12月31日。研究区域为中国大陆地区,地形高度及站点分布如图1所示。
本文插图中所涉及的中国国界基于审图号为GS(2020)4632号标准地图制作,底图无修改。

图1 研究区域地形高度(填色)及站点(黑色圆点)分布Fig.1 Topography(the shaded) of the target area and distribution of stations(black dots)
1.2 数据预处理
1.2.1 数据清洗和质量控制
数据清洗是清除重复、多余的数据,补充缺失数据,纠正或删除错误数据,整理为可进一步加工、使用的数据。对于站点日最高气温观测数据,剔除错误或缺测的站点,得到具有完整时间序列的站点共2238个。站点日最高气温预报值由HRES模式6 h,12 h,18 h和24 h共4个预报时效过去6 h的2 m 温度预报的最大值获得。所有格点上的预报数据采用双线性插值方法插值到站点上[30]。
1.2.2 深度学习特征因子构建
由于神经网络是数据驱动型方法,数据质量对模型有重要影响,因此特征选择尤其重要。根据经验,一般日最高气温出现在14:00—15:00(偶尔出现在傍晚)。用14:00 HRES地面层预报场以及500 hPa,700 hPa和850 hPa气压层预报场中所有要素及组合因子(包括涡度平流和温度平流),以及1.2.1节中得到的HRES模式日最高气温预报值作为初选因子库。为了从初选因子库中挑选出与目标相关的预报因子,采用相关分析法[31]和互信息值法[32]进行特征选择。相关分析法可以挑选出与目标具有一定线性关系的特征,本文用相关分析法选择与目标相关系数大于0.3,且达到0.05显著性水平的因子。互信息值法是通过计算目标与特征间的互信息值,度量特征与目标间的非线性相关性,本文选择互信息值由高至低排名前15的特征。根据两种方法共同挑选的特征有14个,即日最高气温、2 m 温度、2 m露点温度、地表温度、过去6 h的2 m最低温度、过去6 h的2 m最高温度、大气柱水总量、大气柱水汽总量、零度层高度、850 hPa温度、700 hPa温度、500 hPa温度、850 hPa比湿和500 hPa 位势高度;仅相关分析法选择的特征有4个,即对流有效位能、500 hPa比湿、700 hPa比湿和700 hPa位势高度;仅互信息值法选择的特征仅为1个,即平均海平面气压。上述19个因子共同构成特征子集(经过特征选择的HRES因子),并推广至测试集。此外,由于深度学习使用的数据集由不同站点的数据堆叠而成,为了能在数据集中标识不同站点以及样本的时间信息,设计了辅助变量,包括区站号、站点经纬度、站点海拔高度、季节和月份。同时为了避免模型依赖于数值模式预报,基于站点观测的日最高气温,设计了时间滞后变量(滞后1 d日最高气温观测值和滞后2 d日最高气温观测值)。
2 研究方法
2.1 神经网络模型构建
全连接神经网络由相互连接的节点组成,具有相似特征的节点排列在一层[33]。FCNN一般为3层,第1层为输入层,第2层为隐藏层,最后为输出层。信息通过节点之间的连接传输(图2中试验1和试验2)。通过网络拓扑结构,神经网络成为强大的数学模型,几乎可以逼近任意函数。对一般全连接神经网络,不能有效处理分类变量与数值型变量。有时数据集中的特征不仅包含数值型变量,还包含分类变量以区别不同性质的样本,可利用独热编码或者标签编码将不同类别映射为数值处理分类变量。对于独热编码方法[34],分类变量中的类别数极多导致特征空间非常大,引起并行性和多种共线性等问题。对于标签编码方法,将各类别映射为一组有序数字,模型会误认为不同类别存在有序排名(实际上没有),因而对模型性能产生负面影响。
本文为了更好地处理分类变量,并将空间信息和时间信息融入神经网络[35],设计了一种带嵌入层的全连接神经网络(图2中试验3和试验4)。嵌入层源于深度学习中的自然语言处理领域,主要进行词嵌入任务[36]。嵌入层的概念是将正整数(索引)转换为固定大小的稠密向量,提高计算效率,当其与神经网络相连接时,嵌入向量也会在训练神经网络时相应更新。根据嵌入层的原理,嵌入层处理分类变量可以克服独热编码或者标签编码方法的缺陷。因此,本文为了有效处理辅助变量中的区站号和月份这两个分类变量,使神经网络能更好学习到分类变量所传递的信息而设计了嵌入层(图2中试验3)。区站号和月份这两个分类变量经过嵌入层处理后进入神经网络,对于仅有春、夏、秋、冬四类的季节这一特征,可直接应用独热编码方法进行处理,而不送入嵌入层。通过该方式,可避免分季节和分区域建模,仅建立1个模型即可实现全国范围内2238个站点日最高气温的预测任务。在输入数据集中所有样本的空间信息和时间信息已被标识,因此不再分季节和分区域建模,且增加建模使用的数据量有利于神经网络进行表征学习。

图2 多输入全连接神经网络计算流程Fig.2 Flow chart of multi-input fully connected neural network
2.2 试验设计
为了比较不同特征以及嵌入层对模型预报效果的影响程度,本文构建的带有嵌入层的全连接神经网络结构和试验如图2所示,各试验测试目的见表1。由图2可知,试验1的输入特征仅为经过特征选择后的HRES因子,既不添加辅助变量,也不应用嵌入层,直接进入隐藏层;试验2在试验1基础上添加辅助变量1(经度、纬度和海拔)、辅助变量2(季节)和辅助变量3(区站号和月份),经过标签编码的辅助变量3不经过嵌入层处理,直接进入隐藏层;试验3与试验2的不同之处是经过标签编码的辅助变量3经过嵌入层处理进入连接层,最后进入隐藏层(图2);试验4与试验3的不同是在输入层增加时间滞后变量。为方便描述,将不带嵌入层网络架构主体记为FCNN,带有嵌入层的网络架构主体记为ED-FCNN。以上4个试验的目的包括考察嵌入层设计的有效性和评估辅助变量以及时间滞后变量设置的重要性。

表1 不同特征和嵌入层对全连接神经网络结构影响试验设计Table 1 Experiments of features and embedding layers on the structure of multi-input neural network
本文构建的神经网络超参数设置如下:①神经网络中的优化器算法为Adam(adaptive moment estimation),批量大小为64。②正则化方法选为早停法,防止模型过拟合。设定模型迭代时期数为50次,如果训练中验证误差连续3次不降反增,则停止训练,并存储在验证集上表现最佳的模型。③输出层设定为密集层,神经元数量为1,其中激活函数为Linear(线性单元),这是因为输入层和输出层神经元数量分别由输入和输出神经网络中特征数量决定。④对于带有嵌入层的全连接神经网络,设定嵌入层的嵌入向量维度为8。除此之外,图2中隐藏层的神经元数量通过网格搜索方式[37]确定。将ED-FCNN模型隐藏层的神经元个数设置为16,32,64,128,256,512和1024,通过验证集模型的表现效果确定最佳超参数,选定ED-FCNN模型隐藏层的神经元数量为64。
为了检验试验的预报效果,本文根据数值天气预报业务检验的 8 个气候区域(东北、华北、西北地区东部、新疆、长江中下游地区、青藏高原中南部、华南和西南地区东部)[38]分别检验最高气温24 h预报,采用均方根误差、温度预报准确率[39]、温度预报技巧评分[40]、决定系数和平均绝对偏差检验预报效果,其中温度预报准确率为预报值与观测值差值的绝对值不大于2℃的次数与观测总次数之比,该值越大表示预报效果越好。
3 结果分析
3.1 预报误差比较
图3是HRES和神经网络各试验模型预报与观测的散点图。由图3可见,与HRES模式相比,神经网络不同试验模型均能降低原模式的系统预报误差。图3标出每个试验的均方根误差、平均绝对偏差、温度预报准确率和决定系数,比较可知试验4预报效果最优,其次是试验3、试验1和试验2。神经网络试验4模型相对于HRES的均方根误差降幅达47.82%, 温度预报准确率增幅达38.89%,决定系数由订正前的0.975提高至0.992。神经网络各试验模型的预报误差和技巧存在明显差距,初步证明带有嵌入层的全连接神经网络总体效果优于普通全连接神经网络,而且输入网络的特征也影响模型的预报误差和技巧。
图3填色为所有样本点观测值与预报值的核密度图,能直观表现预报的系统误差。核密度图的对角线表示预报和观测完全吻合,对角线两侧密度分布越狭长,说明预报和观测越接近。对HRES模式,大于0℃附近区域内样本拟合线位于对角线下侧,说明HRES模式的日最高气温预报值在暖季整体较观测值偏低,在冷季整体略偏高。试验1~试验4与HRES模式相比,对角线两侧密度分布形状上更加狭长,说明试验1~试验4的预报与观测比HRES模式与观测的相关性更强。试验3和试验4的效果相对更优,紧靠对角线两侧的密度高值区范围更大,主要介于0~30℃,且模型预报值拟合线几乎与对角线重合。试验1和试验2的预报值拟合线在0℃以上几乎与对角线重合,0℃以下变化不大,说明试验1和试验2对于0℃以上订正效果相对更优。
分析神经网络各试验模型结果的不同点发现:试验1是单纯将各站点经特征选择后的预报因子数据堆叠在一起,神经网络模型FCNN在进行表征学习时无法区分各站点样本,因此无法充分挖掘数据中重要信息和规律;加入辅助变量后的试验2,进一步标识每个样本所处的地理位置、海拔高度和时间,这些特征对于广阔区域上的气温预测有明显的指导意义。试验2与试验1相比,试验2的均方根误差略增,但仍比HRES的低。这说明仅仅加入区站号、站点经纬度、站点海拔高度、季节和月份6个辅助变量(试验2),模型可能无法将区站号和月份视为分类变量,有可能仅将其当作数值型数据,造成数据冗余,增加错误信息,影响神经网络模型结果。试验3(ED-FCNN)和试验1(FCNN)与试验2(FCNN)比较表明:在加入辅助变量基础上,应用嵌入层能极大改善神经网络模型的学习效果,试验3与试验1相比均方根误差降幅达16.17%,与试验2相比均方根误差降幅达24.29%。试验4(ED-FCNN)表明在加入辅助变量和应用嵌入层基础上,如果将时间滞后变量也作为特征,神经网络模型预报效果得到进一步改善,试验4与试验3相比均方根误差降幅为11.43%。在数据集中加入时间滞后变量,一是考虑气温在时间上具有一定连续性;二是如果数据集的特征仅包含HRES模式预报因子,经训练后的神经网络模型仅能进行训练数据集中特征与目标规律的学习,导致神经网络模型泛化能力较差,在训练集外新时间段(如测试集时间段)与训练集期间的表现存在差异,加入时间滞后变量后,神经网络模型受HRES模式预报性能的影响减弱。
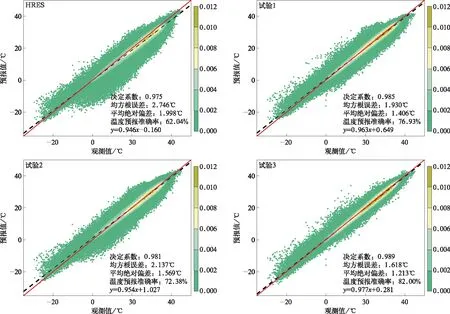

图3 日最高气温预报值与观测值散点图及核密度(红色实线为对角线,黑色虚线为拟合线)Fig.3 Scatter plot and kernel density of daily maximum air temperature between observation and forecasting(the red solid line denotes the diagonal, the black dashed line denotes the fitting line)
以上结果表明:特征的质量可以在一定程度上影响神经网络模型的最终预报效果,但提高神经网络模型效果的最关键因素在于神经网络框架设计,且应充分考虑特征与网络结构间的相互作用机制。试验4的ED-FCNN模型,应用嵌入层处理多类别的分类变量,并设置处理不同类别变量(分类变量与数值型变量)的多输入结构,有利于神经网络捕捉数据中的非线性关系。
3.2 预报技巧
3.2.1 各试验预报技巧空间分布
图4为各试验日最高气温预报技巧评分空间分布,若预报技巧评分为正值且数值越大说明有预报技巧且高;反之,若技巧评分为负值,说明预报无技巧。由图4可以看到,所有神经网络模型在全国范围内大部分区域的预报技巧均为正值,说明神经网络模型是有预报技巧的。
对于试验1,山东南部—广西一线以南地区,山西、甘肃南部、四川中部、云南的预报技巧超过40%~60%,西藏东部、四川西部和云南西部的预报技巧超过60%~80%。但山东半岛、山西南部、陕西中部和云贵高原存在负技巧站点。
对于试验2,试验1预报技巧评分介于20%~40%的大部分站点预报技巧评分在试验2降低至20%以下,且负技巧站点数有所增多,尤其是山东南部—广西一线以南地区。这说明直接加入辅助变量不利于神经网络模型区分不同站点,反而带来更多冗余信息致使站点的预报技巧降低。

图4 日最高气温预报技巧评分(单位:%)Fig.4 Prediction skill score for forecasted daily maximum temperature(unit:%)
与试验1和试验2相比,试验3预报技巧分别超过40%~60%和60%~80%的站点明显增多,负技巧站点数明显减少,仅为辽东湾、山东半岛和陕西的一些站点,且青藏高原东部部分站点的预报技巧超过80%。总体上试验3的预报技巧明显超过试验1和试验2。这是因为经过嵌入层与辅助变量有机结合的ED-FCNN模型可以正确识别辅助变量的信息,说明在大范围空间上,气温特征差异较大,使用标识空间和时间信息的辅助变量有利于校正大面积站点的预报偏差。与试验3相比,试验4大部分站点预报技巧进一步提高,如河北平原和青藏高原等地预报技巧为0~20%的区域大幅缩小,60%~80%的区域显著扩大,预报技巧超过80%的站点范围扩大至青藏高原东部、四川西部和云南北部一带。试验4和试验1~试验3相比,高原和山脉地区的预报技巧明显改善。试验4的ED-FCNN模型能从滞后1 d和2 d日最高气温特征中挖掘真实的气温变化趋势,一定程度上降低其对HRES模式预报的依赖性。
3.2.2 不同误差范围预报技巧
由于预报技巧通过预报绝对偏差的总和计算得到,无法区分预报误差的离散情况,甚至个别大误差会掩盖整个预报技巧的结果,导致预报技巧难以全面反映预报方法优劣。此外,神经网络方法也存在过拟合现象,因此需分析预报正负技巧的具体情况。
表2~表5列出各试验在数值预报业务检验分区的预报技巧等情况。8个分区内各试验的预报正技巧站点占总站点比例平均为86.98%(新疆)~95.69%(华南)(表2),说明各试验预报技巧均有所提高。其中试验1~试验4正技巧的站点占总站点比例分别为79.38%(西北地区东部)~97.46%(华南)、66.67%(新疆)~87.31%(华南)、94.79%(新疆)~99.18%(长江中下游)和98.13%(西北地区东部)~100%(青藏高原中南部、华南),但也看到不同区域预报技巧的提高存在差距。加入嵌入层的试验3在各区域均能取得较好订正效果,说明嵌入层对于站号这种分类变量的处理有效,能帮助识别不同站点的样本,改善不同区域站点的预报技巧。加入时间滞后变量的试验4能在试验3基础上进一步减小各区域误差。试验4显著提高了新疆、西北地区东部、青藏高原中南部和西南地区东部正技巧站点比例。
比较日最高气温的预报正技巧站点平均绝对偏差不超过2℃的站点比例(表3),试验1~试验4各区域的站点比例分别介于57.75%(青藏高原中南部)~99.07%(华北)、51.52%(青藏高原中南部)~98.89%(华北)、79.49%(青藏高原中南部)~100.00%(西北地区东部)和98.73%(青藏高原中南部)~100.00%(东北、新疆、西北地区东部、华北和华南),且在所有区域中试验1~试验4在青藏高原中南部平均绝对偏差不超过2℃的正技巧站点比例相对最低。即使这样,试验3显著提高了青藏高原中南部和西南地区东部的平均绝对偏差不超过2℃的正技巧站点比例(比试验1分别提高21.74%和14.17%),试验4显著提高了上述两个地区的平均绝对偏差不超过2℃的正技巧站点比例(比试验1分别提高40.98%和20.33%),且试验4在8个区域中平均绝对偏差不超过2℃的正技巧站点比例达100%的有5个区,其他区域接近99%,优于试验1~试验3,说明试验4不仅正技巧站点最多,而且也能更好地降低绝大部分站点平均绝对偏差。对于试验1~试验4,各区域正技巧站点平均绝对偏差不超过1℃的站点比例(表4)中,西南地区东部站点比例相对最低,华北站点比例相对最高。各试验平均技巧评分最低值均出现在东北区(平均为19.50%),最高值均出现在青藏高原中南部(平均为62.75%)。对比各试验不同区域平均正技巧评分,试验4预报效果均最佳(表5)。
预报正技巧站点所占比例较高,负技巧站点所占比例就较低,其反映的规律和正技巧的类似,因此不再赘述。

表2 各试验不同区域的正技巧站点比例(单位:%)Table 2 Ratio of positive skills in different regions(unit:%)

表3 各试验不同区域平均绝对偏差不超过2℃的正技巧站点比例(单位:%)Table 3 Positive skill ratio of mean absolute error no more than 2℃ in different regions(unit:%)

表4 各试验不同区域平均绝对偏差不超过1℃的正技巧站点比例(单位:%)Table 4 Positive skill ratio of mean absolute error no more than 1℃ in different regions(unit:%)

表5 各试验不同区域平均正技巧评分(单位:%)Table 5 Average positive skill scores in different regions(unit:%)
以上分析表明,本节结果与3.1节一致,带有嵌入层的全连接神经网络加入辅助变量和时间滞后变量作为特征,不仅能够增加正技巧站点数量,而且能使更多站点平均绝对偏差降低至1℃以下。在数据集中掺杂冗余信息的试验2中,各指标结果与其他试验相比更差,因此正确衡量特征对于神经网络结构的作用极其重要,对克服神经网络的过拟合现象,捕捉数据中的非线性关系,改善日最高气温的预报效果有显著作用。
3.3 预报误差随时间变化特征
图5是各试验模型在测试集1—12月日最高气温预报的均方根误差箱线图。由图5可以看到,试验1~试验4均方根误差的箱体均比HRES模式低,说明各月份的均方根误差均能被大幅度降低,且箱体外没有离群点出现,说明HRES模式和各试验模型的均方根误差数据分布中不包含极端情况,各月份预报均方根误差较为稳定。对比HRES模式以及试验1~试验4,每个模型预报的均方根误差箱体长度相当,说明预报的均方根误差在1—12月内差别不大,预报误差随时间变化不大。HRES模式与试验1~试验4各箱体四分位间距(上下四分位数间的距离)分别为0.35℃,0.26℃,0.39℃,0.25℃ 和0.19℃,试验4不仅最小,且平均数与中位数居于箱体中间位置,分别为1.43℃和1.41℃,说明试验4预报的1—12月均方根误差分布处于无偏状态,模型在各月的日最高气温预报性能更为稳定。

图5 测试集中HRES和各试验预报的1—12月均方根误差箱线图Fig.5 Box plot of root mean square error of HRES and each test in test dataset during Jan-Dec
试验1中,经FCNN模型订正后不同月份误差比HRES模式更低更集中,可能是因为FCNN模型能从时间长度为5年的训练集中学习到不同特征在时间上的规律,选用的气象变量(如气温相关变量)一般具有自相关性和周期性规律,因此通过长时间训练集的学习,FCNN模型可以一定程度上消除HRES模式在季节上的预报偏差。在试验1基础上加入辅助变量并应用嵌入层后的试验3表现效果更优,因为辅助变量包含季节和月份两个标识样本时间信息的变量,使试验3的ED-FCNN模型可以正确区分不同季节特征因子的差异,通过该方式可以有效降低针对不同季节单独建模的复杂程度[19],同时保留足够的样本进行深度特征挖掘。在试验3基础上加入时间滞后变量后的试验4箱体位置最低且集中度最高,说明时间滞后变量对预报日预报量同样有重要影响,因为如果无明显的天气系统影响,气温变化应平缓,不会发生骤变或转折,那么其参考价值将很高。
4 结论与讨论
本文利用欧洲中期天气预报中心(ECMWF)高分辨率确定性模式HRES的输出产品和中国国家级地面气象站的日最高气温数据,构建24 h最高气温预报神经网络模型。为了考察辅助变量、时间滞后变量设置的重要性和神经网络中嵌入层对分类变量处理的有效性,基于全连接神经网络设计4个试验建模,并与HRES日最高气温预报对比,评估辅助变量、时间滞后变量以及嵌入层对神经网络模型学习效果的影响。结论如下:
1) 加入辅助变量、时间滞后变量的特征和带有嵌入层的深度学习神经网络模型的组合试验对HRES的24 h日最高气温预报均有订正效果,可将预报均方根误差降低29.72%~47.82%,温度预报准确率提高16.67%~38.89%。加入辅助变量且对分类变量经过嵌入层处理显著提高了青藏高原中南部和西南地区东部的平均绝对偏差不超过2℃的正技巧站点比例(比试验1分别提高21.74%和14.17%),在此基础上加入时间滞后变量显著提高上述两个地区的平均绝对偏差不超过2℃的正技巧站点比例(比试验1分别提高40.98%和20.33%),且预报性能更加稳定。
2) 由于普通全连接神经网络(FCNN)模型无法将区站号和月份等辅助变量视作分类变量,在进行表征学习时将其视作数值型数据造成数据冗余,增加错误信息,影响神经网络模型结果。因此,对于分类变量,需进行单独处理再输入模型才能使神经网络的数据学习更充分。如果不对分类变量进行处理,可能需要分区域建模(不设置区站号这一分类变量)或分季节建模(不设置季节这一分类变量),会降低预测效率。
3) 使用带有嵌入层的全连接神经网络时,如果在数据集中进一步加入辅助变量,包括坐标信息、地理信息和时间信息以及时间滞后变量等特征,并应用嵌入层处理分类变量(如区站号与月份),能发挥特征的作用,使模型更好地学习数据中的特征关系,得到更优的订正效果。
4) 由于训练后的神经网络模型仅能学习到训练数据集中特征与目标的规律,但该规律未必适应新的数据集,导致神经网络模型泛化能力较差,可能在新时间段(如测试集时间段)的表现与训练集存在差异,加入时间滞后变量后,可将神经网络模型受HRES模式的影响减弱。
总之,在深度学习中,神经网络学习性能不仅取决于特征因子的选择(辅助变量、时间滞后变量),还取决于神经网络结构(例如加入嵌入层)的设计。特征质量一定程度上可以影响神经网络模型的最终预报效果,但提高神经网络模型效果的最关键因素在于设计神经网络框架,并充分考虑特征与网络结构间的相互作用机制。此外,超参数的选择也非常重要,本文的超参数选择限定了优化器的算法和批量大小。下一步可优化超参数选取过程,进一步加深网络深度,探索不同正则化方法以提高模型的泛化能力。

