基于FDM-VBF的低雷诺数串列双圆柱绕流数值模拟

赵 海 栋， 王 超， 任 冰， 陈 卫 东， 王 国 玉

(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024 )

0 引 言

当水流经过圆柱时，圆柱背流面的两侧会发生交替的漩涡脱落，这种周期性的漩涡脱落会使圆柱受到横流向和顺流向流体力作用．该现象广泛存在于工程实际中，比如海洋石油的输油管道、钻井平台的立管和海底管线等．在实际工程的圆柱结构中，圆柱一般是成组出现，所以双圆柱绕流问题是国内外海洋工程学者更为关注的问题．

Meneghini等[1]采用有限单元法对Re=100～200串列和并列布置的两个圆柱进行了数值模拟．Alam[2]采用有限体积法对Re=200串列双圆柱进行了研究，分析了上下游圆柱漩涡脱落的相位滞后对升力的影响．Zhou等[3]采用有限单元法，使用大涡模拟进行紊流计算，对Re=1 000的串列双圆柱进行了数值模拟．刘松等[4]采用有限体积法对Re=200串列双圆柱进行了研究，分析了不同间距比对圆柱间相互作用和尾流特征的影响．Alam等[5]通过物理模型实验，得到了亚临界雷诺数下串列双圆柱的受力情况．王龙军[6]对非等直径串列双圆柱的绕流特性进行了系统的实验研究．

然而，目前的研究中少有采用有限差分法(FDM)进行圆柱绕流的数值模拟，原因在于传统的有限差分法一般采用结构化网格，很难模拟复杂结构物的边界．Peskin[7]提出的浸入边界法(IBM)给这一问题提供了解决思路，该方法通过在结构物附近采用离散的力来模拟结构与流体之间的相互作用，代替流固界面处的物面边界条件．Fadlun等[8]基于有限差分法和浸入边界法，提出了一种二阶精度、高效的数值计算方法，该方法可用于解决具有复杂几何形状的物体与三维不可压缩流体的流固耦合问题．Liu等[9]则进一步发展了这种方法，将浸入边界法和流体体积法(VOF)结合获得虚拟边界力法(VBF)，再结合有限差分法，使得该方法在处理包含自由面、复杂几何形状结构物和运动物体的流固耦合问题上具有很大的优势．

此外，不少学者如Kumar等[10]、Sohankar[11]研究过阻塞率对于圆柱绕流数值计算结果的影响，但少有学者注意到上游圆柱中心与入口的距离对数值计算结果的影响，这一参数足够大时，才能更好地模拟实际海洋工程中的圆柱绕流问题．

基于以上两点，展开本文的工作．基于Liu等[9]的工作，应用有限差分法和虚拟边界力法，建立求解均匀流作用下不同间距比的串列双圆柱绕流的数学模型．对数值计算的控制方程、边界条件进行介绍，同时对计算域大小、网格收敛性和流场三维效应进行分析；对间距比在2.0～5.0的串列双圆柱绕流问题进行数值模拟，分析不同间距比下漩涡脱落现象，及上下游圆柱阻力系数、升力系数和斯特劳哈尔数随间距比变化的趋势．

1 数值计算模型

1.1 控制方程

本文采用不可压缩的连续方程和黏性的N-S方程作为描述流体运动的基本控制方程：

∇·u=0

(1)

(2)

式中：u为流体速度，t为时间，ρ为流体密度，p为流体压强，ν为运动黏度，g为重力加速度．相较于通用的N-S方程，上式右端增加了一项虚拟边界力fVBF用于表示结构物对流体的作用力，fVBF的计算见下文．

本文采用经典的两步映射算法对流体的控制方程进行数值离散，两步映射算法执行过程如下：

第一步

(3)

第二步

(4)

(5)

(6)

数值模型基于有限差分法，采用非均匀交错网格划分计算域，其中矢量(如作用力、速度等)定义在网格面心上，标量(如压强、密度等)定义在网格体心上．采用虚拟边界力法处理结构物边界，实现结构物和流场之间的数据交互．由于传统的一阶迎风格式会在计算过程中引入过多的数值耗散，而中心差分格式常会导致数值计算的不稳定，本文中对流项采用迎风格式与中心差分格式相结合的混合差分格式进行离散，可以在减少数值耗散的同时提高计算的稳定性，扩散项则采用中心差分格式离散．

1.2 边界条件

流域边界条件按物理量分为速度边界和压强边界，如下：

(1)速度入口边界设置为均匀流，即u=0.01 m/s，v=0 m/s；出口边界设置为开放边界，假定出口处流体流动已经衰退为均匀流动状态，速度沿出口法线方向梯度为零，∂u/∂x=0，∂v/∂x=0；上下边界设置为自由滑移边界条件，即∂u/∂y=0，v=0 m/s；流固界面条件设置为无滑移和不可穿透固体边界．

(2)压强入口边界、出口边界及上下边界均设置为零梯度边界，沿边界法线方向梯度为零．

1.3 数值计算域

为保证数值计算的精度和效率，对Re=200串列双圆柱的数值计算域进行讨论，并与Alam[2]的计算结果进行对比．选择圆柱中心间距比L*=4的工况：圆柱绕流数值模拟采用雷诺相似，上下游圆柱直径D均为0.1 m，均匀来流速度u0为0.01 m/s，由Re=u0D/ν经计算得运动黏度ν=5.0×10-6s/m2．

(1)计算域收敛性验证

串列双圆柱的计算域布置见图1．

图1 串列双圆柱的计算域Fig.1 Computational domain for two tandem cylinders

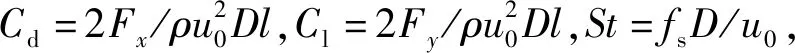
表1 串列双圆柱的计算域收敛性分析Tab.1 Computational domain convergence analysis for two tandem cylinders

表1中序号1、2所代表的计算域均为40D×30D，此时只改变Lu、Ld的相对取值，计算结果相差很大，最大为10.2%(Cl1，max)，最小也有4.2%(Cd1，mean)；序号1、3所代表的计算域中Ld=31D，此时只改变Lu的取值(5D、15D)，计算结果相差很大，最大为11.6%(Cl2,max)，最小也有5.7%(St)；可见Lu的取值对计算结果影响很大，原因在于来流为均匀流，至上游圆柱前端速度降为零，有较大的速度梯度，需要足够的网格解析度和空间来捕捉流场演变．3、4号计算域与5号计算域的计算结果除Cd2，mean(7.5%，7.0%)外，相对差值均在5%以内．6号计算域65D×30D与文献[2]的计算域完全一致，两者计算结果相对差值最大值只有2.4%(Cd1，mean)，而与5号计算域的计算结果相对差值最大值有5.4%(Cd1，mean)．本文后续计算均选取最大的5号计算域100D×80D，以保证入口处的均匀来流以及减少阻塞率对于流体流速的影响，精度较高．同时本文采用等比格式划分网格，边缘区域网格较大，故加大计算域，网格数量增加相对较少，从而对计算效率影响较小．

(2)网格收敛性验证

为提升计算效率，避免资源浪费，同时保证数值计算精度，进行网格收敛性验证，计算结果见表2．最小网格1/50D、1/40D、1/30D的计算结果相差均在1.5%以内，所以最小网格选择1/30D，这样既可保证计算精度，又能提高计算效率．

表2 串列双圆柱的网格收敛性分析Tab.2 Grid convergence analysis for two tandem cylinders

(3)二维、三维数值模拟结果对比

为确定Re=200串列双圆柱的适用模型维度，进行了三维数值模拟．圆柱长度设置为3.2D，网格数为32，计算结果为Cd1，mean=1.235，Cl1，max=0.719，Cd2，mean=0.347，Cl2，max=1.512，St=0.170．从图2可知，Re=200的涡量场没有明显的三维现象．对比表2中二维数值模拟的计算结果差别极小．故就目前的计算需求来说，本文使用二维数值模型进行计算．图2中涡量的计算公式为Ωz=∂v/∂x-∂u/∂y，涡量使用均匀来流速度u0和圆柱直径D进行量纲一化．

图2 串列双圆柱的三维瞬时涡量场Fig.2 The three-dimensional instantaneous vorticity field of two tandem cylinders

2 数值计算结果与分析

使用建立好的数值模型模拟了Re=200、间距比L*=2.0～5.0的串列双圆柱的圆柱绕流，将数值计算结果与文献[2]进行了比较，结果详见表3．

从表3可以看出，本文与文献[2]在各系数的计算中趋势一致，绝对差值均在0.043以内．在Cd1，mean计算中，本文与文献[2]相对差值均在±3%以内；在Cd2，mean计算中，本文与文献[2]相对差值较大，在L*=3.5时达到了95.56%，但由于基数较小，绝对差值只有0.043，综合考虑在可接受范围内；St的相对差值只有在L*=2.0时达到了6.35%，其余情况相对差值均在±4%以内．Wang等[12]也进行过L*=2.0的串列双圆柱的绕流计算，其中Cd1，mean=1.039，Cd2，mean=-0.198，St=0.133，与本文计算结果更加相符．计算结果差值产生的原因是本文采用的计算域100D×80D，相较于文献[2]的计算域65D×30D更大，更能保证入口是均匀来流，以及减少阻塞率对流体流速的影响，这在计算域收敛性验证中已经进行过讨论，另一方面原因来自于数值计算方法的差异．

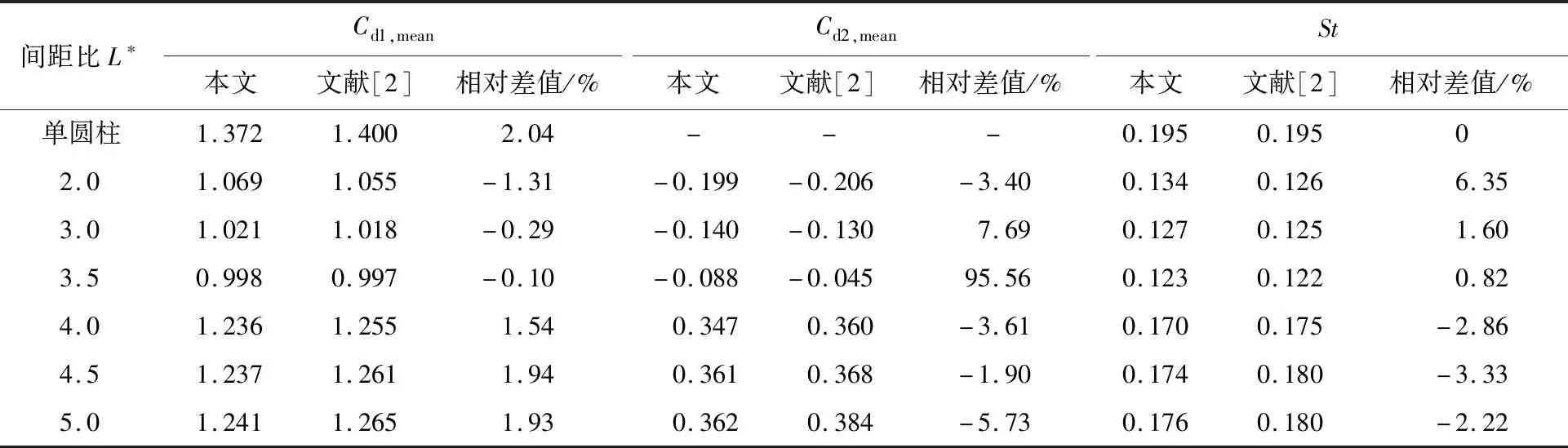
表3 串列双圆柱在不同间距比下的计算结果Tab.3 The computational result of two tandem cylinders at different spacing ratios

串列双圆柱各间距比的瞬时涡量场见图3．由图3可知，当间距比为2.0、3.0、3.5时，为再附着状态(reattachment)，上游圆柱分离的剪切层会重新附着到下游圆柱上，上下游圆柱之间会形成对称的漩涡．当间距比为4.0、4.5、5.0时，为同脱落状态(co-shedding)，上下游圆柱均有漩涡脱落．从再附着状态到同脱落状态转变的间距比称为临界间距比Lcr．

为进一步研究Re=200串列双圆柱绕流的临界间距比Lcr，本文又计算了间距比为3.6、3.7、3.8、3.9的工况，与表3的数值计算结果一同绘制在图4～7中，可见临界间距比约为3.7．

图4、5分别展示了上下游圆柱平均阻力系数随间距比L*变化的趋势．当L*<3.7时，Cd1，mean

(a)L*=2.0

图4 上游圆柱在不同间距比下的平均阻力系数Fig.4 The mean drag coefficients of the upstream cylinder at different spacing ratios

图5 下游圆柱在不同间距比下的平均阻力系数Fig.5 The mean drag coefficients of the downstream cylinder at different spacing ratios

随着L*的增大而减小，Cd2，mean随着L*的增大而增大，这与剪切层附着点有关．L*>3.7时，上下游圆柱均有漩涡脱落，Cd1，mean和Cd2，mean均急剧增加后缓慢增加；随着间距比的增大，上游圆柱阻力系数受下游圆柱的影响越来越小，趋向于单圆柱状态，而下游圆柱处于上游圆柱的尾流中，其阻力系数虽有所增大，但仍保持较小值．

图6展示了斯特劳哈尔数随间距比变化的趋势．当L*<3.7时，随着间距比的增大，上游圆柱分离的剪切层需要更多的时间重新附着到下游圆柱，然后从下游圆柱脱落，完成漩涡脱落的循环，进而导致St逐渐减小．当L*>3.7时，上下游圆柱均有漩涡脱落，St激增至0.175后，随着间距比的增大，缓慢逼近单圆柱的St．

图6 串列双圆柱在不同间距比下的斯特劳哈尔数Fig.6 The Strouhal number of two tandem cylinders at different spacing ratios

图7展示了本数值模型中上下游圆柱的升力系数最大值随间距比变化的趋势，水平线代表单圆柱绕流的升力系数最大值．在L*<3.7时，上游圆柱没有漩涡脱落，升力系数几乎为零，且随间距比的增大基本保持不变；随着间距比的增大，上游圆柱分离的剪切层至下游圆柱时，流速恢复到更高的水平，导致下游圆柱升力系数缓慢上升，在L*=3.7时达到单圆柱升力系数的55.8%．在L*>3.7时，上下游圆柱均有漩涡脱落，升力系数均急剧增长；随着间距比的增大，上游圆柱受下游圆柱的影响越来越弱，升力系数基本与单圆柱升力系数持平；下游圆柱在上游圆柱的尾流中，不仅受自身泻涡的影响，还受上游圆柱泻涡的影响，升力系数急剧增长为单圆柱升力系数的2倍左右，但随着间距比的增大，上游圆柱的泻涡至下游圆柱前端会慢慢衰退，逐渐恢复至均匀流，对下游圆柱的影响越来越小．可以预见，超过某一间距比后，上下游圆柱均表现得与单圆柱无异．

图7 上下游圆柱在不同间距比下的升力系数最大值Fig.7 The maximum lift coefficients of upstream and downstream cylinders at different spacing ratios

3 结 论

(1)在对计算域收敛性验证的过程中发现，上游圆柱中心与入口的距离对数值模拟的结果具有较大影响，基于本文数值结果，这个距离要在15D以上才能保证数值计算的精度．

(2)Re=200条件下，三维数值模型中涡量场不存在明显的三维特性，上下游圆柱阻力系数、升力系数及斯特劳哈尔数的计算结果与二维数值模型基本一致，可以使用二维数值模型进行计算．

(3)Re=200条件下，串列双圆柱的漩涡脱落状态从再附着状态到同脱落状态转变的临界间距比为3.7．

(4)低于临界间距比时，上游圆柱分离的剪切层重新附着到下游圆柱上，上下游圆柱之间会形成对称的漩涡，漩涡只从下游圆柱脱落．随着间距比的增大，Cd1，mean和St逐渐减小，Cd2，mean和Cl2，max逐渐增大，Cl1，max几乎保持不变．

(5)超过临界间距比时，上下游圆柱均有漩涡脱落，上下游圆柱阻力系数、升力系数及斯特劳哈尔数均有突增．随着间距比的增大，上游圆柱阻力系数和升力系数受下游圆柱的影响越来越小，趋向于单圆柱状态；下游圆柱处于上游圆柱的尾流中，其阻力系数虽有所增大，但仍保持较小值，升力系数相当于单圆柱升力系数的2倍左右，同时随着间距比的增大，有下降的趋势．可以预见，超过某一间距比后，上下游圆柱均表现得与单圆柱无异．