颗粒形状对粗粒土密实度的影响研究

刘波 刘鹏 马刚 杨平荣 王一涵 冷天培

摘要：密实度是衡量粗粒土力学性能的重要指标之一。大量实验表明，颗粒形状对颗粒材料的密实度有显著的影响，但针对特定形状指标对密实度影响的研究较少。选取大石峡堆石坝料场的卵石料颗粒和块石料颗粒作为试验材料，通过三维扫描获取颗粒的真实形状，计算了颗粒的形状指标。基于颗粒的真实形状，构建模拟真实粗粒土颗粒的离散元团簇体模型。采用压缩边界法对颗粒集合体进行制样，并对所有试样孔隙比进行测定。BP神经网络与Olden方法相结合的参数敏感性分析显示：对密实度敏感性较强的形状指标依次为三维球度、凸度、三维圆度和二维圆度，颗粒的三维球度指标能够较好地反映粗粒土密实度随颗粒形状的变化规律。考虑粗粒土颗粒三维球度的正态分布特性，针对三维球度呈不同正态分布的试样进行数值模拟，结果表明：试样的孔隙比随颗粒三维球度分布范围的增大基本保持不变，其分布范围的变化对孔隙比的影响较小。

关 键 词：粗粒土; 颗粒形状; 密实度; 孔隙比; 形状指标; 离散元; 神经网络

中图法分类号： TV641.4

文献标志碼： A

DOI：10.16232/j.cnki.1001-4179.2022.04.025

0 引 言

粗粒土作为堆石坝的主要建筑材料，也广泛应用于道路、矿山、港口等的工程建设中。在高堆石坝工程中，坝体的变形对大坝的运行特性和安全有着重要的影响，而坝体堆石的密实度是衡量堆石体压缩变形的重要因素。因此，对堆石坝工程中粗粒土料密实度的研究和预测具有着重要的现实意义[1-3]。粗粒土作为典型的散粒体材料，其密实度受许多因素的影响。孙晨等[4]探讨了不同粒径颗粒土体堆积的松密程度。朱俊高等[5]通过离散元的方法模拟了不同级配下颗粒试样的三轴剪切试验，结果表明当不同级配的颗粒试样处于相同的孔隙率时，相对密实度会有较大差别。文喜南等[6]基于颗粒堆积模型预测了粗粒土的最小孔隙比。

由于自然界中的粗粒土颗粒形状各异，颗粒形状对颗粒材料密实度的影响一直备受研究人员的关注。长期以来，许多学者通过物理试验或数值模拟的方法对各种形状的颗粒进行研究，常见的颗粒形状包括球体[7-8]、椭球体[9-10]、圆柱体[11-12]、立方体[13-14]、四面体[15-16]、胶囊状体[17]等。土石颗粒的形状各异，X射线扫描[18-19]、3D扫描仪[20-21]等3D图像技术的引入让颗粒真实形状的获取成为了可能。基于颗粒的三维形状，学者们计算球度、圆度、凸度等形状指标来表征颗粒的形状，继而研究颗粒形状与密实度之间的关系。Cho等[22]采用线性方程描述了不同形状指标与均一粒径砂的孔隙比的关系。除考虑颗粒形状的自身变化外，Chang等[23]进一步考虑了颗粒形状与颗粒粒径之间的相关性，认为均一粒径砂的最大或最小孔隙比受到砂粒粒径大小和形状指标双重因素的影响。考虑到仅针对单一变量进行研究的局限性，Zheng等[24]统计了相关文献中的142种砂样的颗粒粒径、颗粒形状、级配特征以及所对应的极限孔隙比，并增加25组试验数据进行综合分析，结果表明：颗粒形状指标中的圆度、球度以及颗粒粒径的分散度对砂粒的孔隙比影响较大，而颗粒粒径的具体大小对孔隙比的影响很小。

上述理论研究、室内试验和数值模拟都探讨了颗粒形状对粗粒土密实度的影响，但并没有针对每个形状指标给出较为具体的结论。本文选取大石峡堆石坝料场的卵石料颗粒和块石料颗粒作为试验材料，通过粗粒土的孔隙比反映其密实度，利用三维扫描获取颗粒的真实形状。基于颗粒的真实形状，构建模拟真实粗粒土颗粒的离散元团簇体模型，对所有试样孔隙比进行测定，并采用BP神经网络与Olden方法相结合的参数敏感性分析方法对不同形状指标的敏感性进行分析，探讨对土体密实度影响最大的形状指标，并针对颗粒形状参数的分布特性进行相应的研究。

1 颗粒扫描和形状统计分析

本文选取大石峡堆石坝料场的卵石料颗粒和块石料颗粒作为试验材料，采用三维激光扫描技术获取真实粗粒土颗粒表面点云数据，通过三维重构算法重构颗粒模型，获得颗粒三维形状信息。扫描后得到的卵石料颗粒和块石料颗粒如图1所示。通过粒径筛选，得到了10～20 mm，20～40 mm和40～60 mm 3个粒径组的颗粒。

为描述粗粒土形状的具体特征和变化规律，需对颗粒的形状指标进行提取和分析。Zheng[25-26]等将描述颗粒形状的指标分为外形、圆度和表面纹理3个层次。邹德高[27]、张家发[28]等分别采用伸长率、扁平率、球度、分形维数等量化颗粒的形状特征。为简化不规则颗粒形状指标的提取，岩土工程中常用颗粒二维投影面的形状获取二维形状指标。Rodriguez等[29]整理了5种常见的二维球度定义，包括面积球度、直径球度、圆比例球度、周长球度和宽长比球度。Wadell[30-32]提出了颗粒二维圆度的概念，通过计算颗粒投影面角点的曲率来计算颗粒的圆度，其计算公式如下：

R=Ni=1ri/Nrins（1）

式中：ri为投影面第i个角点处的曲率圆半径;rins为投影面最大内切圆半径;N为投影面的角点个数。

可类比式（1）求得颗粒的三维圆度，式中ri类比为颗粒第i个顶点处的曲率半径;rins为颗粒的最大内切球半径;N为颗粒顶点个数。

本文采用二维和三维形状参数相结合的方式对颗粒的形状参数进行提取和分析。基于三维扫描所得到的真实颗粒形状，经过信息化处理计算颗粒的三维圆度[30-32]和中长轴比、短中轴比、三维球度、凸度、Domokos系数共6个三维形状指标：

EI=I/L               中长轴比FI=S/I短中轴比φ3D=336πV2/A三维球度CX=V/Vch  凸度Sf=1S+1I+1L S2+I2+L2/3 Domokos系数（2）

式中：S，I，L分别代表颗粒的短轴、中轴和长轴长度;V代表颗粒体积;A表示颗粒的表面积;Vch表示颗粒外包凸多面体的体积。

基于三维颗粒形状模型，找到颗粒投影面积最大的侧面，将此面的投影输出为图像。采用Zheng等[25]开发的图像处理技术提取颗粒的二维形状指标，如图2所示。根据投影面形状信息计算Wadell二维圆度。

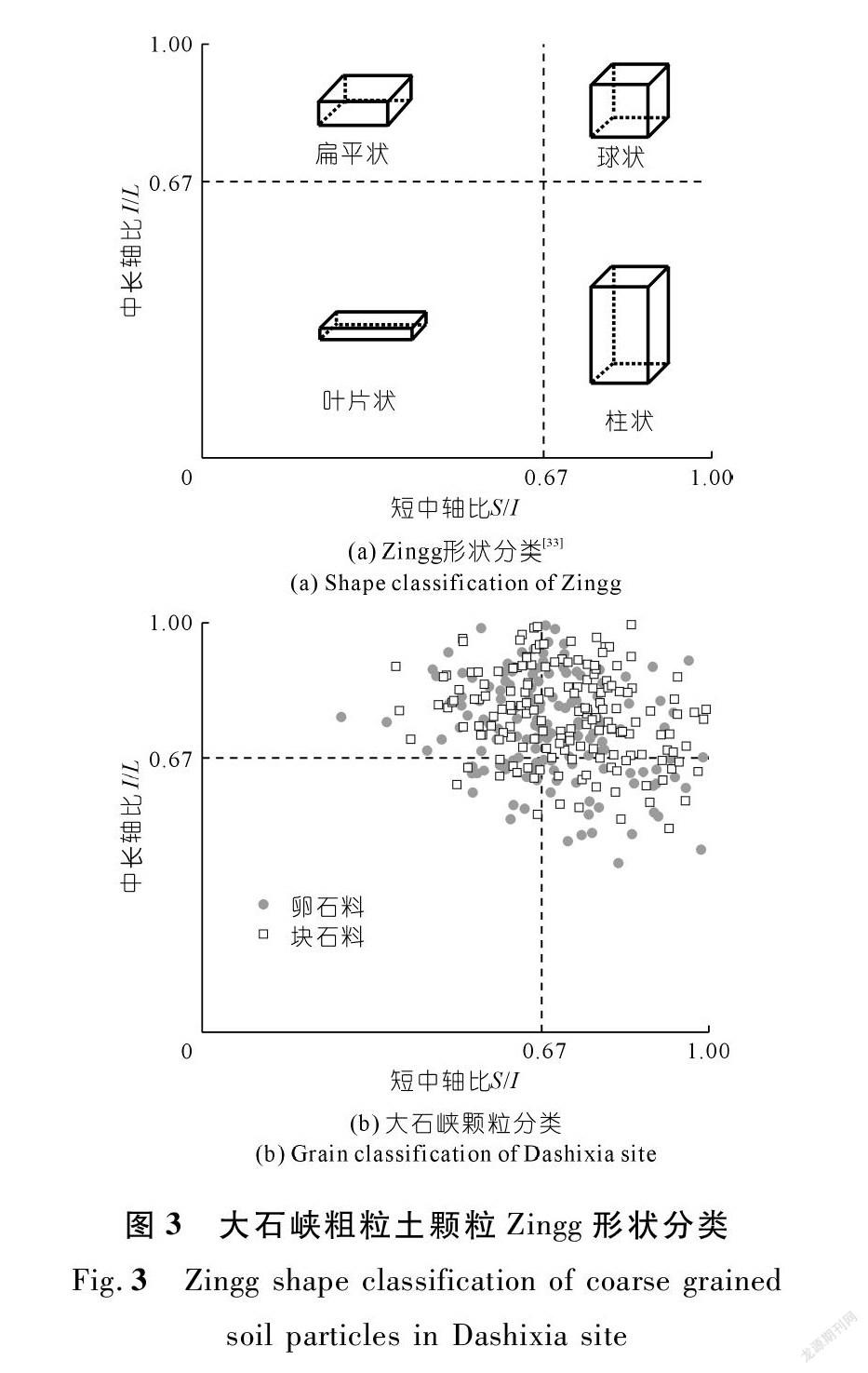
如图3（a）所示，Zingg根据颗粒的短中轴长度比和中长轴长度比将颗粒形状大致划分为扁平状、球状、叶片状和柱状4类。将大石峡粗粒土颗粒按照上述规则进行分类，如图3（b）所示，卵石料和块石料在4种类型均有分布，叶片状颗粒占比较少。块石料中球状颗粒和扁平状颗粒相对较多，柱状颗粒数量相对较少;卵石料中球状颗粒、扁平状颗粒和柱状颗粒的数量相当。

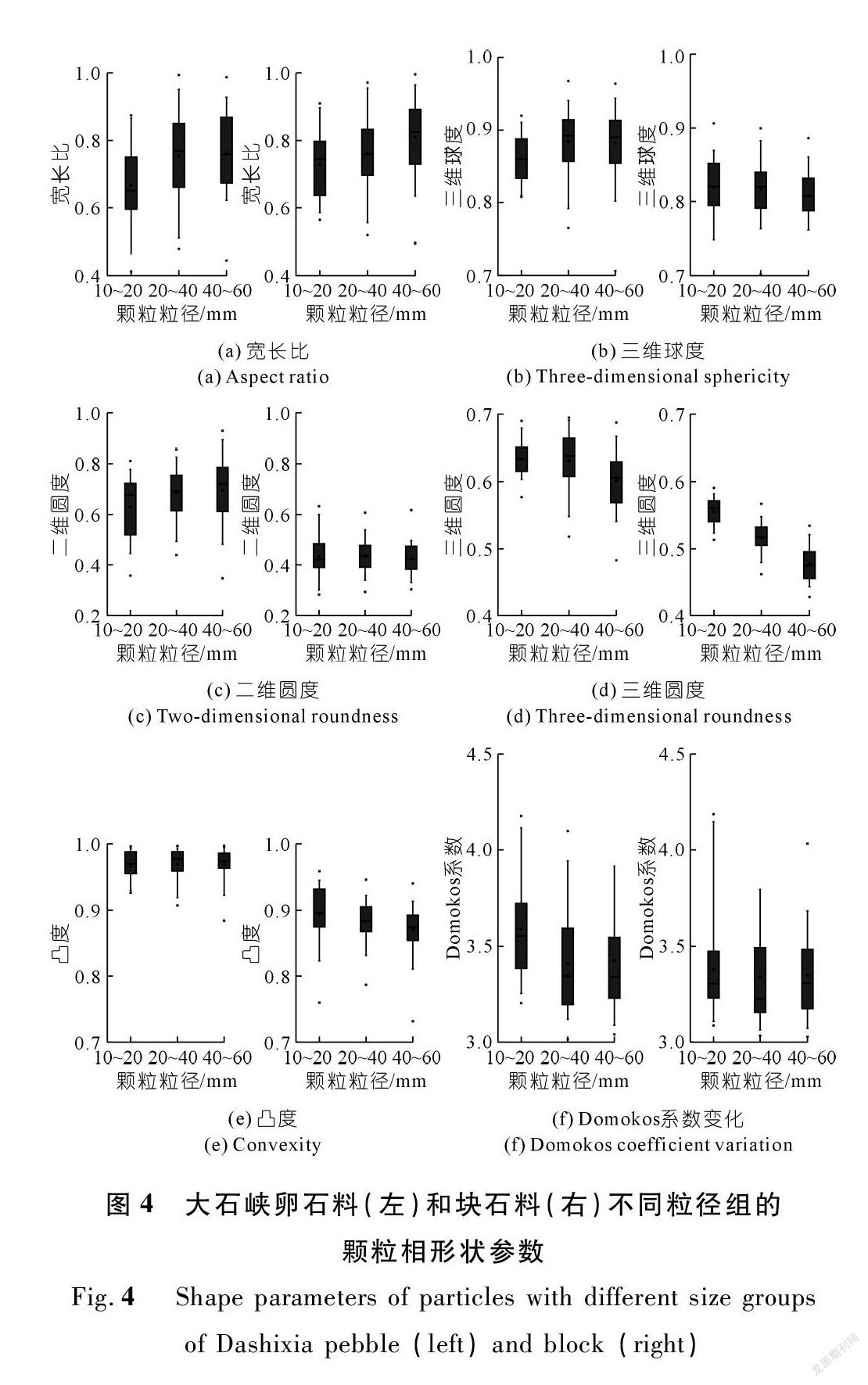
考虑到颗粒粒径对颗粒形状的影响，本文对两组颗粒的不同粒径组形状指标进行统计分析。如图4所示，卵石料和块石料颗粒的宽长比均随粒径的增大而增大，二者对应分布范围也十分相近。对于三维球度，卵石料颗粒随粒径变化呈一定的增大趋势，而块石料的三维球度略微降低但整体变动较小，因此随着粒径的增大，卵石颗粒更加浑圆，而块石颗粒没有明显变化，并且卵石颗粒的三维球度整体大于块石颗粒。两种颗粒的二维圆度随粒径的增大变化不大，而三维圆度均随粒径的增大而减小，因此颗粒的二维圆度和三维圆度反映了不同方面的形状特征。卵石颗粒的二维圆度、三维圆度以及凸度指标整体均大于块石颗粒。Domokos系数随粒径的变化不明显。综上所述，随颗粒粒径的增大，卵石料颗粒的整体形状更加规则圆润，棱角更为平滑，而块石料颗粒形状的整体变化相对较小。

2 颗粒形状参数对密实度的影响

2.1 基于离散元的颗粒堆积模拟

基于三维扫描得到的粗粒土真实颗粒形状，构建模拟真实粗粒土颗粒形状的离散元团簇体模型[33-35]。本文采用Taghavi[36]提出的泡沫填充算法（bubble packing algorithm）构建离散元团簇体颗粒来模拟粗粒土的真实颗粒形状。泡沫填充算法有两个控制参数，分别为颗粒中最小与最大泡沫的粒径比ρ和颗粒光滑度的测量角度φ，即相邻两个泡沫球的交角。当φ=0时，两个小球外部相切;当φ=180°时，一个小球完全内切于另一小球。不同参数取值下的真实颗粒形状模拟效果如图5所示，小球的数量随参数ρ的减小和φ的增大而增加，颗粒形状的模拟也更加精确。考虑到形状模拟的精确程度与计算成本之间的平衡，本文选取ρ=0.2，φ=150°，对应每个团簇体颗粒均由约120个小球组成。该算法已被集成入离散元计算软件PFC3D内部。

本文采用压缩边界法进行颗粒集合体的制样，具体步骤如下：

（1） 生成试样。在0.3 m×0.3 m×0.6 m的空间范围内随机生成等效粒径（与试样颗粒体积等同的球体直径）为30 mm的形状一致、大小相等、无相互接触的团聚体颗粒。为消除固定边界的影响，制样空间的四周采用周期性边界。

（2） 压缩边界。在无重力作用的条件下，上下两侧采用刚性加载板作为颗粒集合体试样的上下边界，缓慢移动上下加载板直至达到预先给定的荷载值，板的移动速度随自身压强的大小而不断调整，在靠近目标荷载的过程中线性递减。本文荷载值设置为5 kPa，制样过程中板的最大移动速度为0.1 m/s。

（3） 平衡试样。采用伺服机使试样在稳定的荷载下逐渐达到平衡，当颗粒集合体的总动能小于0.001 J时则认定其达到稳定平衡状态，颗粒之间的接触作用采用Hertz模型。计算参数见表1。

从大石峡粗粒土颗粒的三维扫描文件中选取100个不同形状的颗粒，其中卵石颗粒和块石颗粒各占一半。按照上述试验方法进行数值试验，获取对应各自形状指标的均一粒径颗粒集合体的孔隙比。每组试样中的颗粒数目以尽可能充满制样空间为标准，试样的加载过程和生成试样如图6所示。

对加载完成后的100组试样其孔隙比进行测定，所有试样的孔隙比均在0.65～1.10之间。其中50个卵石样本颗粒集合体试样的孔隙比平均值为0.728，最大值为0.876，最小值为0.655;50个块石样本颗粒集合体试样的孔隙比平均值为0.813，最大值为1.100，最小值0.709。块石颗粒集合体的孔隙比整体上大于卵石颗粒集合体的孔隙比。每组试样中的颗粒数目以尽可能充满制样空间为准，平均每组试样颗粒数为900个左右。

2.2 颗粒形状参数敏感性分析

为研究不同形状指标对粗粒土孔隙比的影响，本文采用BP神经网络与Olden方法相结合的参数敏感性分析方法对上述不同形状指标的敏感性进行分析[37]。其实现方式为：首先通过训练BP神经网络建立颗粒形状指标与孔隙比之间的映射关系，然后基于神经网络各层之间的连接权值，采用Olden算法分析各输入参数的敏感性程度。Olden算法又称连接权值法，是一种评估各个输入变量对输出变量影响程度的方法，计算公式如下：

Oik=lj=1ωijυjk（3）

式中：Oik为输入变量xi对输出变量yk的敏感性指標值;ωij为输入变量xi（i=1，2，…，N）与隐含层神经元j（j=1，2，…，L）之间的连接权值;υjk为隐含层神经元j（j=1，2，…，L）与输出变量yk（k=1，2，…，M）之间的连接权值。Oik绝对值越大，代表该变量对输出结果的影响程度（敏感性）越大[37]。

粗粒土颗粒集合体的孔隙比与形状指标的敏感性计算分析过程如下：

（1） 选择测试指标。选取归一化处理的颗粒形状指标作为BP神经网络的输入层变量，包括中长轴比、三维球度、二维圆度、三维圆度、凸度和Domokos系数，输出结果为颗粒集合体的孔隙比。

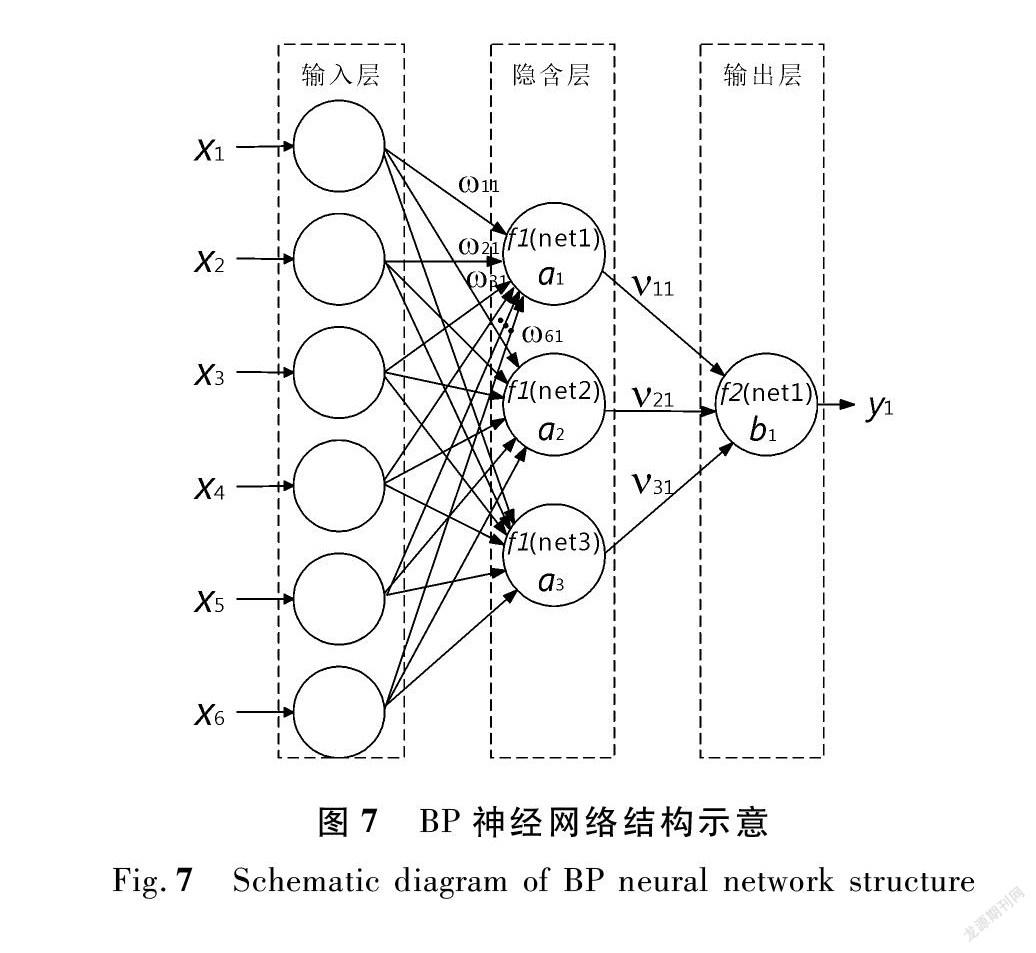
（2） BP神经网络的训练。从100组试验样本中随机抽取80组作为训练样本，其余20组为预测样本。为使BP神经网络具有良好的预测效果和泛化能力，经比选采用（6-3-1）三层BP神经网络，神经网络的结构示意图如图7所示。最大训练次数为1 000，训练要求精度为10-5，学习率为0.1。经多次神经网络训练，选用预测效果最佳的神经网络，模型预测效果如图8所示。

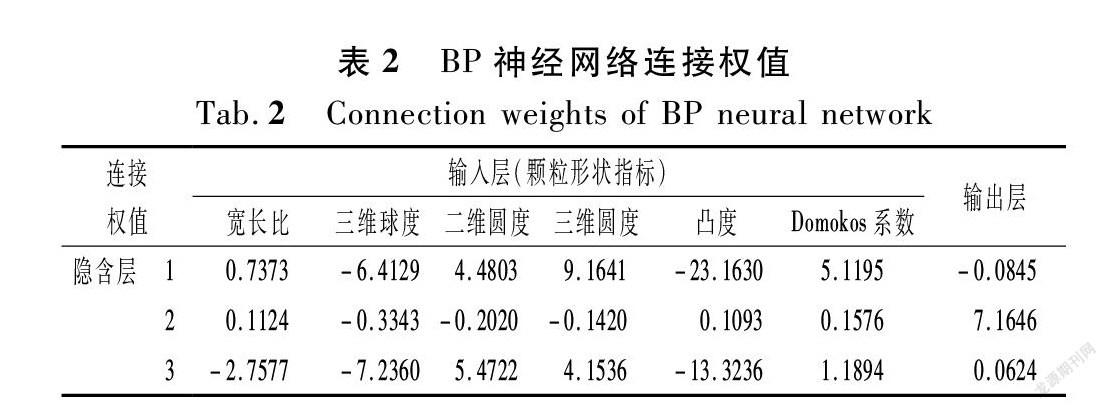
（3） BP神经网络连接权值的提取。提取训练完成的BP神经网络输入层与隐含层、隐含层与输出层之间的连接权值，提取结果如表2所列。

（4） Olden方法求解敏感性指标值。将第（3）步中提取的神经网络连接权值代入式（3）计算敏感性指标值。

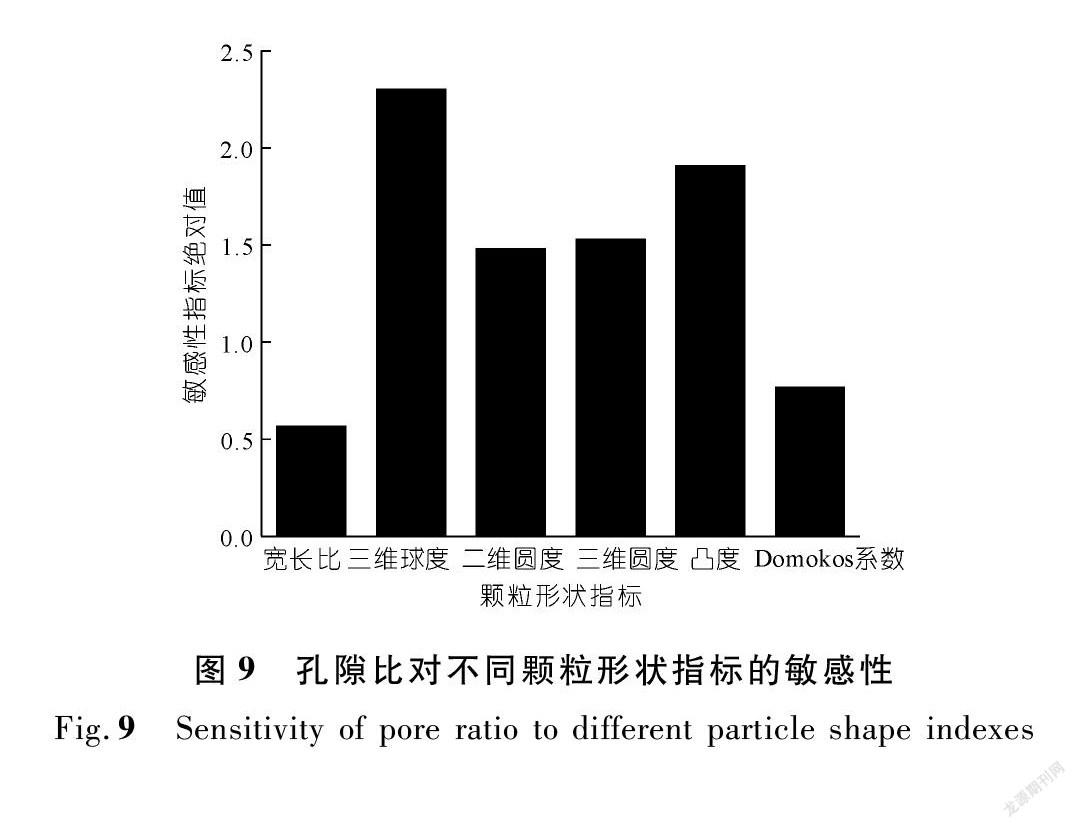
孔隙比对不同颗粒形状指标的敏感性结果如图9所示，6种颗粒形状指标中，孔隙比对颗粒的三维球度的敏感性最强，其次分别为颗粒的凸度、三维圆度和二维圆度，而对中长轴比和Domokos系数的敏感性相对较弱。

2.3 密实度变化规律

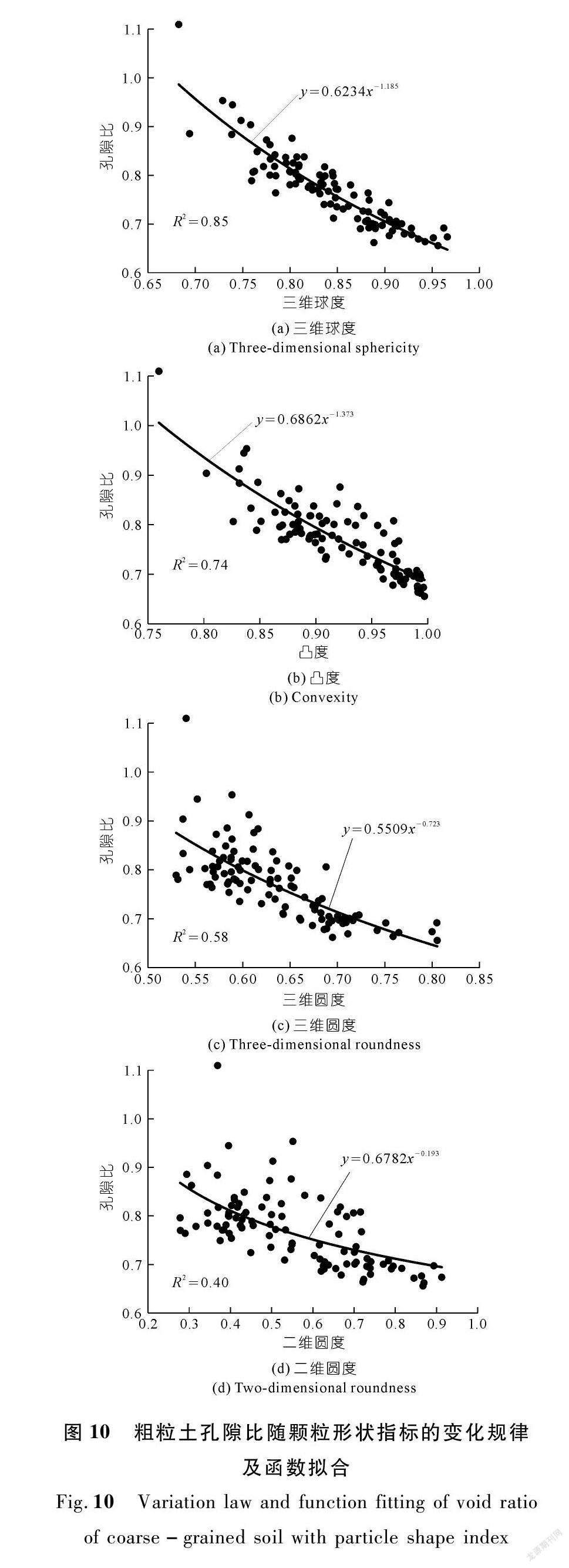
基于孔隙比与颗粒形状指标之间敏感性的分析结果，本文针对敏感性较强的4种形状指标，三维球度、凸度、三维圆度和二维圆度，具体分析孔隙比随各形状指标的变化规律。

如图10所示，对于4种颗粒形状指标，孔隙比值均随形状指标的增大而减小。采用幂函数拟合各形状指标与孔隙比之间的关系，其中孔隙比随颗粒三维球度的变化规律最为明显，函数拟合的相关系数R2达0.85;对于颗粒凸度、三维圆度和二维圆度，函数拟合的效果依次减弱，孔隙比变化的规律性依次减小。因此，颗粒的三维球度指标能够更好地反映粗粒土孔隙比的变化规律，颗粒形状越接近于球形则堆积越为密实。

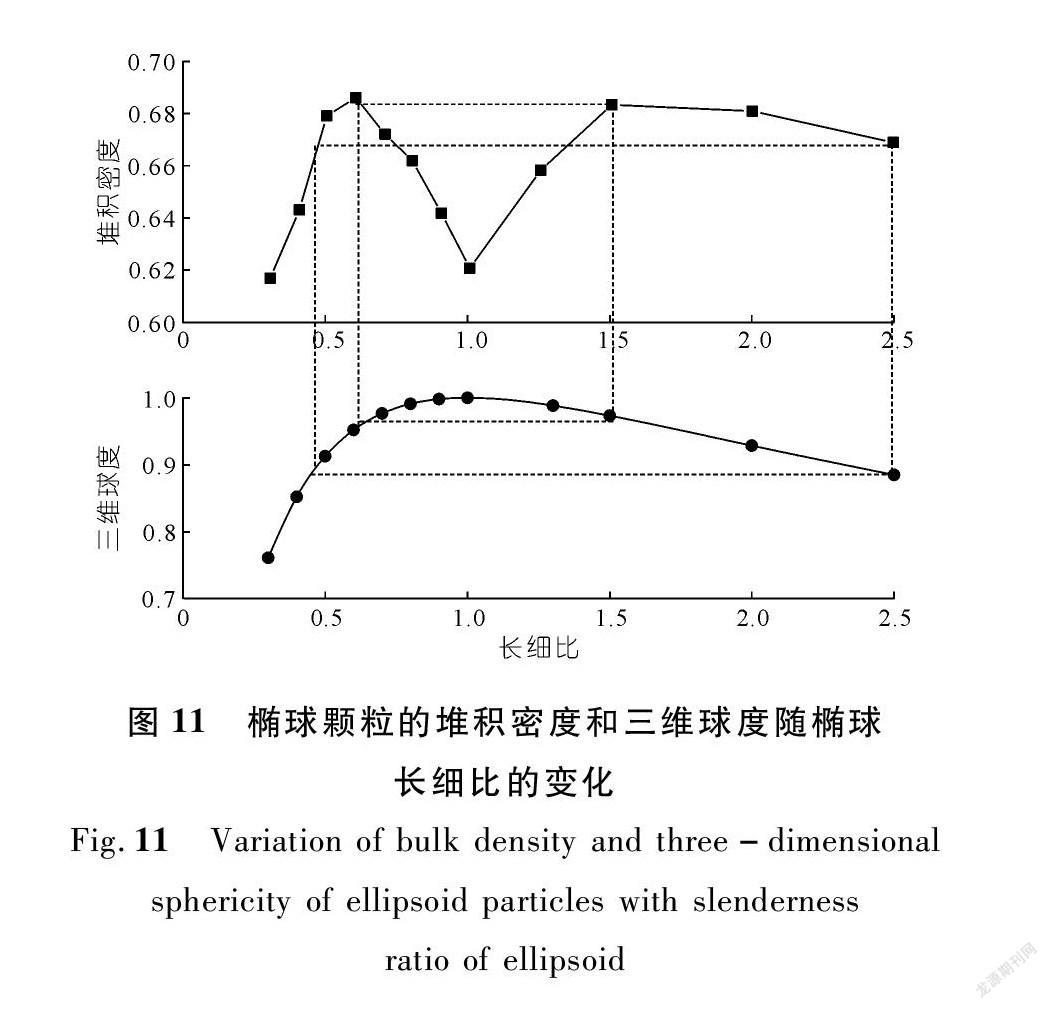
为了探讨颗粒三维球度对密实度影响的适用性，本文对比了椭球颗粒集合体的堆积密度随椭球长细比的变化规律。如图11所示，其中堆积密度定义为颗粒体积占总体积之比，赵仕威[38]将其描述为“M”型曲线。图11中长细比为1.0代表圆球颗粒，大于1.0代表长细的椭球颗粒，小于1.0代表扁平的椭球颗粒。曲线的两峰值点所对应的椭球长细比分别在0.6和1.5附近，其对应三维球度均在0.97左右，与本文粗粒土颗粒三维球度指标的最大值相近。在两峰值点外侧的区域，椭球颗粒的三维球度值均小于0.97，表现出堆积密度随球度值的减小而减小，对应于孔隙比的增大;而在两峰值点内侧的区域，堆积密度随颗粒三维球度值的增大而减小，对应于孔隙比的增大。三维球度相等的椭球颗粒（如长细比分别为2.50和0.47），其颗粒集合体的堆积密度也基本相同。

因此，考虑到土石颗粒为天然形成的产物，其形状特征受到母岩特性、迁移历史、开采方式等诸多因素的影响，不易形成几近球形的颗粒，所以在其相应的形状变化范围内，密实度基本随三维球度指标的增大而提高。

3 颗粒形状分布特性对密实度的影响

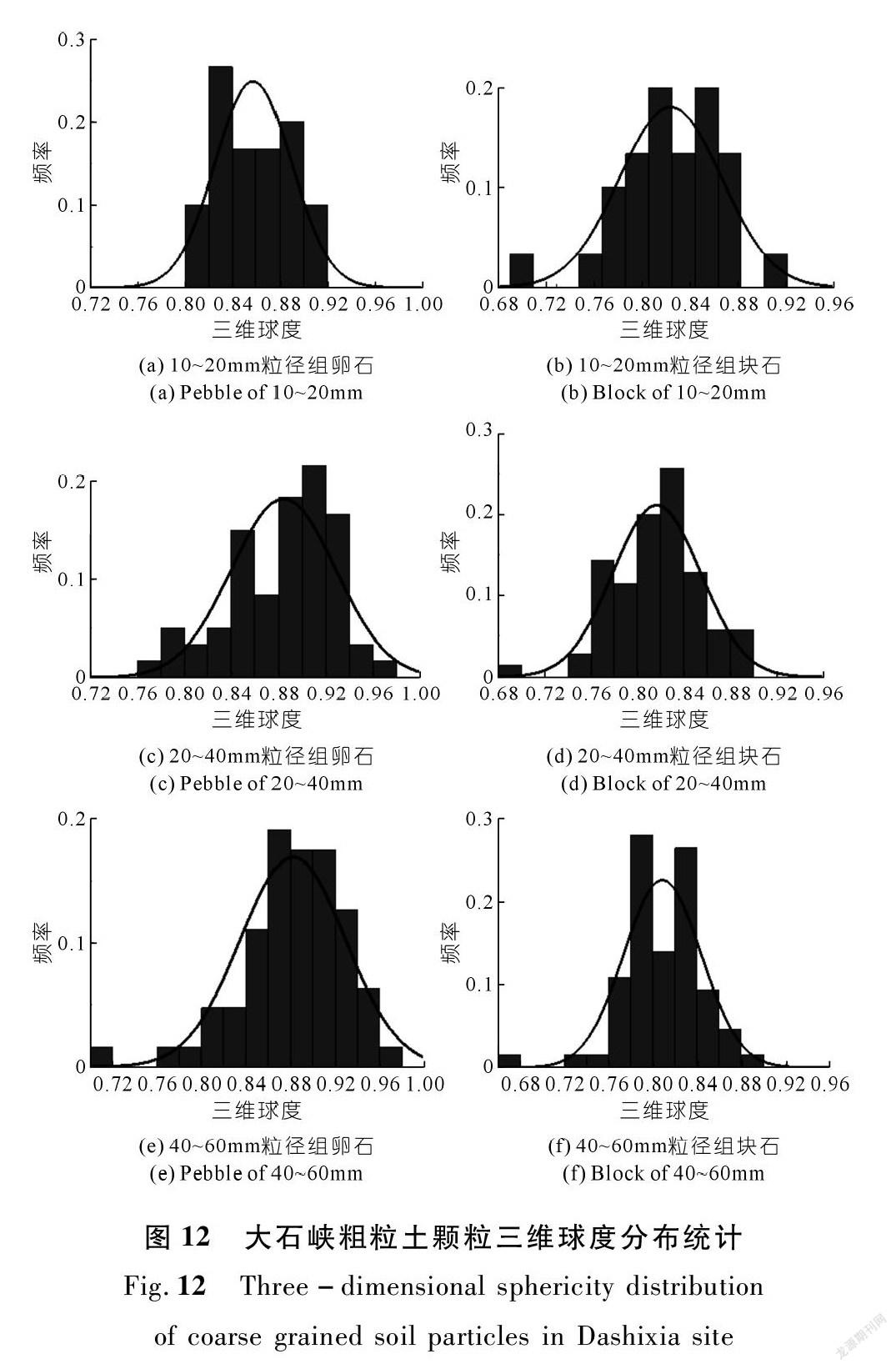
实际情况中，同一粒径组内粗粒土颗粒的形状各异。为考虑颗粒形状的差异性，本文对各粒径组粗粒土颗粒的三维球度做进一步统计分析。如图12所示，各粒径组颗粒三维球度大致呈正态分布。采用统计学中的Kolmogorov-Smirnov检验法，对各组样本进行正态分布检验，结果在α=0.05的显著性水平下接受原假设，因此认为样本服从正态分布。

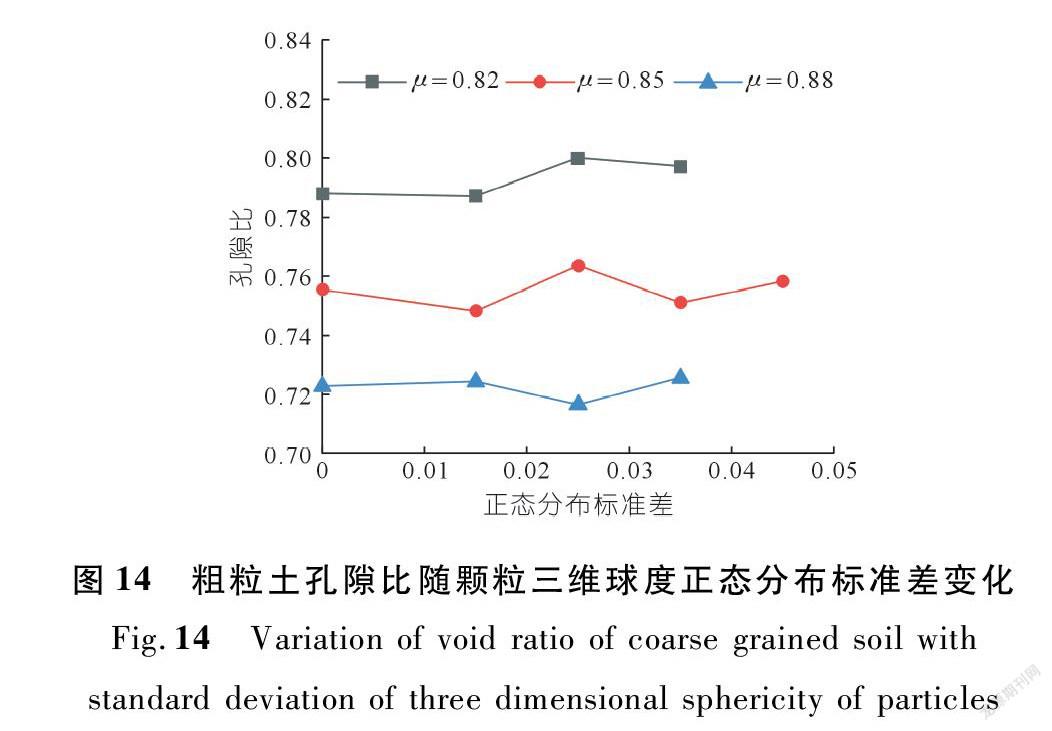
考虑粗粒土颗粒三维球度的正态分布特性，本文设计了3组试验样本，样本内颗粒三维球度分布按照预先设计的正态分布特征生成。如图13所示，3组样本的颗粒三维球度均值分别为0.82，0.85和0.88，标准差分别取为0.015，0.025，0.035（和0.045），按照3σ原则截取颗粒三维球度的分布范围。其中第一组生成的试样均由块石颗粒组成，第三组生成的试样均由卵石颗粒组成，第二组生成的试样由块石和卵石颗粒混合组成。试样生成和加载过程与3.1节相同。

3组试样的孔隙比随颗粒三维球度标准差变化的结果如图14所示。由图可知，各组试样随颗粒三维球度分布范围的增大，孔隙比结果仅有较小变化，考虑到随机误差，可认为试样的孔隙比随颗粒三维球度分布范围的增大而基本保持不变，且无论卵石颗粒和块石颗粒的占比，均表现出一致的规律。

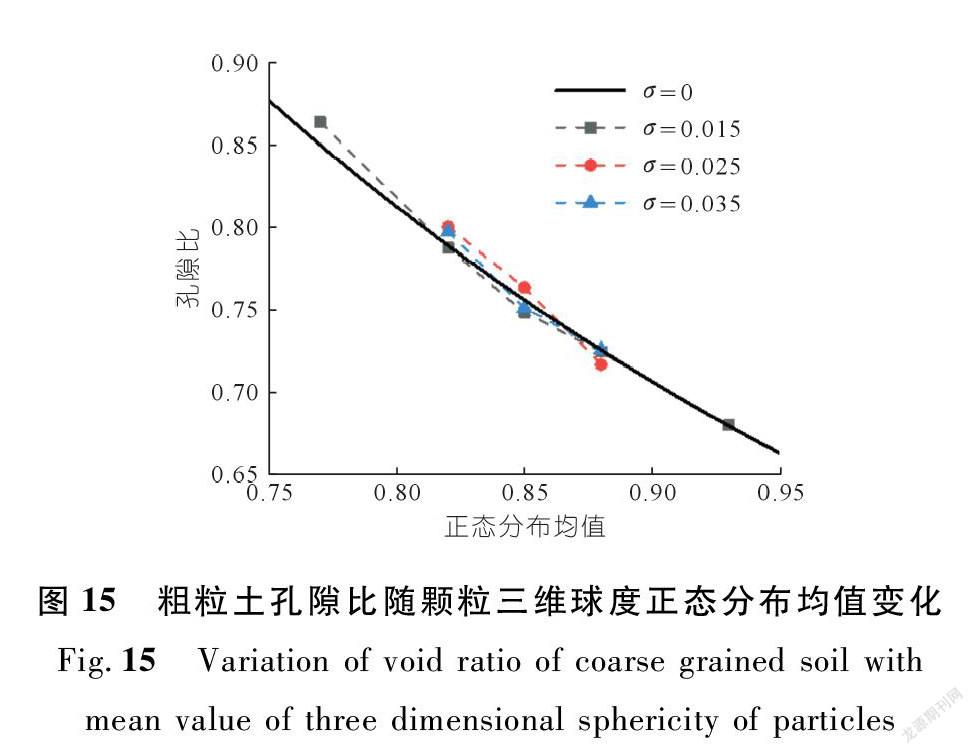
试样的孔隙比结果随三维球度均值的变化规律如图15所示，其与3.3节孔隙比随颗粒三维球度变化的拟合曲线基本重合。因此，粗粒土颗粒三维球度均值与孔隙比之间存在较好的对应关系，并且其分布范围的变化对孔隙比的影响较小。

4 结 论

（1） 选取的试验材料中，扁平状、球状和柱状颗粒均有分布，叶片状颗粒较少。整体而言，随颗粒粒径的增大，卵石料颗粒的整体形状更加规则圆润，棱角更为平滑，而块石料颗粒形状的整体变化相对较小。

（2） 针对密实度对不同形状指标的敏感性进行分析，敏感性较强的指标依次为三维球度、凸度、三维圆度和二维圆度。孔隙比随颗粒三维球度指标变化的规律最为明显，表现为随三维球度的增大而减小。采用幂函数拟合三维球度与孔隙比之间的关系R2可达0.85，因此采用颗粒的三维球度指标能够较好地反映粗粒土密实度随颗粒形状的变化规律。

（3） 对大石峡粗粒土各粒径组颗粒的三维球度指标进行统计检验，其正态分布的规律性较强。进行不同正态分布均值和标准差的颗粒试样试验，结果表明试样的孔隙比随颗粒三维球度分布范围的增大基本保持不变，三维球度均值与粗粒土孔隙比之间存在较好的对應关系，其分布范围的变化对孔隙比的影响较小。

参考文献：

[1] ZHOU W，XU K，MA G，et al.Effects of particle size ratio on the macro-and microscopic behaviors of binary mixtures at the maximum packing efficiency state [J].Granular Matter，2016，18（4）：81.

[2] 马刚，周伟，常晓林，等，堆石料缩尺效应的细观机制研究[J].岩石力学与工程学报，2012，31（12）：2473-2482.

[3] 周伟，常晓林，马刚，等.堆石体缩尺效应研究进展分析[J].水电与抽水蓄能，2017，3（1）：17-23.

[4] 孙晨，韩文喜，王昊.不同粒径对粗粒土力学参数影响的研究[J].人民长江，2018，49（10）：97-103.

[5] 朱俊高，郭萬里，徐佳成，等.级配和密实度对粗粒土三轴试验影响离散元分析[J].重庆交通大学学报（自然科学版），2017，36（6）：70-74.

[6] 文喜南，马刚，王峰，等.基于颗粒堆积模型预测粗粒土最小孔隙比[J].水力发电学报，2020，39（3）：78-87.

[7] LI C X，AN X Z，YANG R Y，et al.Experimental study on the packing of uniform spheres under three-dimensional vibration[J].Powder Technology，2011（208）：617-622.

[8] REIMANN J，VICENTE J，BRUN E，et al.X-ray tomography investigations of mono-sized sphere packing structures in cylindrical containers[J].Powder Technology，2017（318）：471-483.

[9] ZHAO S，ZHANG N，ZHOU X，et al.Particle shape effects on fabric of granular random packing[J].Powder Technology，2017（310）：175-186.

[10] DONEV A，CISSE I，SACHS D，et al.Improving the density of jammed disordered packings using ellipsoids[J].Science，2004，303（5660）：990-993.

[11] QIAN Q，AN X，WANG Y，et al.Physical study on the vibrated packing densification of mono-sized cylindrical particles[J].Particuology，2016（29）：120-125.

[12] TANGRI H，GUO Y，CURTIS J S.Packing of cylindrical particles：DEM simulations and experimental measurements[J].Powder Technology，2017（317）：72-82.

[13] WU Y，AN X，YU A B.DEM simulation of cubical particle packing under mechanical vibration[J].Powder Technology，2017（314）：89-101.

[14] XIE Z，AN X，WU Y，et al.Experimental study on the packing of cubic particles under three-dimensional vibration[J].Powder Technology，2017（317）：13-22.

[15] ZHAO B，AN X，WANG Y，et al.DEM dynamic simulation of tetrahedral particle packing under 3D mechanical vibration[J].Powder Technology，2017（317）：171-180.

[16] ZHAO J，LI S X，JIN W W，et al.Shape effects on the random-packing density of tetrahedral particles[J].Physical Review E，2012（86）：31307.

[17] AL-RAOUSH R.Microstructure characterization of granular materials[J].Physica A：Statistical Mechanics and its Applications，2007，377（2）：545-558.

[18] ALSHIBLI K A，DRUCKREY A M，AL-RAOUSH R I，et al.Quantifying morphology of sands using 3D imaging[J].Journal of Materials in Civil Engineering，2015，27（10）：376 04014275.

[19] FONSECA J，O’SULLIVAN C，COOP M R，et al.Non-invasive characterization of particle morphology of natural sands[J].Soils and Foundations，2012，52（4）：712-722.

[20] HUANG Q，ZHOU W，MA G，et al.Experimental and numerical investigation of Weibullian behavior of grain crushing strength[J].Geoscience Frontiers，2020，11（2）：401-411.

[21] LATHAM J P，MUNJIZA A，GARCIA X，et al.Three-dimensional particle shape acquisition and use of shape library for DEM and FEM/DEM simulation[J].Minerals Engineering，2008，21（11）：797-805.

[22] CHO G，DODDS J，SANTAMARINA J C.Particle shape effects on packing density，stiffness，and strength：natural and crushed sands[J].Journal of Geotechnical and Geoenvironmental Engineering，2006，132：591-602.

[23] CHANG C S，DENG Y，MEIDANI M.A multi-variable equation for relationship between limiting void ratios of uniform sands and morphological characteristics of their particles[J].Engineering Geology，2018（237）：21-31.

[24] ZHENG J，HRYCIW R D.Index void ratios of sands from their intrinsic properties[J].Journal of Geotechnical and Geoenvironmental Engineering，2016，142（12）：11-19.

[25] ZHENG J，HRYCIW R D.Traditional soil particle sphericity，roundness and surface roughness by computational geometry[J].Géotechnique，2015，65（6）：494-506.

[26] ZHENG J，HRYCIW R D.Roundness and sphericity of soil particles in assemblies by computational geometry[J].Journal of Computing in Civil Engineering，2016，30（6）：4016021.

[27] 邹德高，田继荣，刘京茂，等.堆石料三维形状量化及其对颗粒破碎的影响[J].岩土力学，2018，39（10）：3525-3530.

[28] 张家发，叶加兵，陈劲松，等.碎石颗粒形状测量与评定的初步研究[J].岩土力学，2016，37（2）：343-349.

[29] RODRIGUEZ J M，JOHANSSON J M A，EDESKAR T.Particle shape determination by two-dimensional image analysis in geotechnical engineering[J].Proceedings of Nordic Conference on Soil Mechanics and Geotechnics，2012：207-218.

[30] WADELL H.Volume，shape and roundness of rock particles [J].The Journal of Geology，1932，40（5）：443-451.

[31] WADELL H.Sphericity and roundness of rock particles[J].The Journal of Geology，1933，41（3）：310-331.

[32] WADELL H.Volume，shape and roundness of quartz particles[J].The Journal of Geology，1935，43（3）：250-280.

[33] 周偉，刘东，马刚，等.基于随机散粒体模型的堆石体真三轴数值试验研究[J].岩土工程学报，2012，34（4）：748-755.

[34] 徐琨，周伟，马刚，等.基于离散元法的颗粒破碎模拟研究进展[J].岩土工程学报，2018，40（5）：110-119.

[35] ZHOU W，LIU J，MA G，et al.Three-dimensional DEM investigation of critical state and dilatancy behaviors of granular materials[J].Acta Geotechnica，2017，12（3）：1-14.

[36] TAGHAVI R.Automatic clump generation based on mid-surface[C]∥Proceedings of 2nd International FLAC/DEM Symposium，Melbourne，2011.

[37] 陈文森，常晓林，马刚，等.基于神经网络连接权值的堆石体流变模型参数敏感性研究[J].中国农村水利水电，2018（1）：128-134.

[38] 赵仕威.颗粒材料物理力学特性的离散元研究[D].广州：华南理工大学，2018.

（编辑：郑 毅）

Effect of grain morphology on compactness of coarse-grained soils

LIU Bo1，LIU Peng 1，MA Gang2，YANG Pingrong1，WANG Yihan2，LENG Tianpei2

（1.Jiangxi Provincial Water Conservancy Planning Design And Research Institute，Nanchang 330000，China; 2.State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China）

Abstract：

Compactness is one of the most important criteria to measure the mechanical behaviors of coarse-grained soils.Abundant experiments show that the grain morphology has a significant influence on the compactness of granular materials，but few researchers focus on the effects of specific shape descriptors.In this paper，the pebble grains and block grains of Dashixia rockfill dam were selected as the materials，and the morphology of the grains was obtained by 3D scanning.Then we calculated the shape descriptors of grains.Based on the morphology，a discrete element cluster model was established to simulate the coarse-grained soil grains.The grain aggregate was prepared by using the compression boundary method，and the void ratios of all samples were measured.Parameter sensitivity analysis combined with BP neural network and Olden method showed that the shape descriptors with strong sensitivity to compactness were three-dimensional sphericity，convex，three-dimensional roundness and two-dimensional roundness in turn.According to normal distribution of the three-dimensional sphericity of coarse-grained soil grains，a numerical simulation was carried out considering different normal distributions of the three-dimensional sphericity.It showed that the void ratios of the samples basically remained unchanged with the increasing of distribution range of three-dimensional sphericity，and the change of the distribution range had little effect on the void ratio.

Key words：

coarse-grained soil;grain morphology;compactness;void ratio;shape descriptor;DEM;neural network