单摆测重力加速度实验数据可视化平台的设计与实现
郝振莉,时金蒙,吕良军
(1. 黄河水利职业技术学院,河南 开封 475004;2. 数学建模教学与应用研究中心,河南 开封 475004)
0 引言
在传统的大学物理实验课程教学中, 一般要求学生通过实验获得实验数据, 并对实验数据进行计算处理,从而实现实验目的。 同时,也可以通过计算结果判断实验数据的准确性。由于计算烦琐复杂,人工计算不仅花费大量的时间,还容易出错。计算机的普及和相应软件的开发开启了信息技术与教育教学深度融合的新篇章。 教育部《2018 年教育信息化和网络安全工作要点》 中提到:“促进信息技术与教育教学融合发展仍是当今教育信息化工作的重点,要培养提升教师和学生的信息素养”[1]。 笔者以“单摆测重力加速度实验”为案例,利用Matlab GUI 平台,设计开发单摆实验数据可视化平台, 将抽象的理论知识动态化、可视化,使学生进一步理解、掌握课程内容,从而学生激发学习大学物理实验课程的兴趣,使之乐于学习钻研。
1 实验原理
在物理实验中, 测量重力加速度的常用方法有复摆法、单摆法、多普勒效应等。其中,单摆法操作最简单,且精度较高,应用较为广泛。
1.1 单摆测重力加速度的数学模型
如图1 所示,1 根细线(长度变化、质量在精度要求不高时可忽略不计)的一端固定在A 点,另一端悬挂一体积很小的质量为m 的小球,当细线静止地处在竖直位置时,小球在位置O,此时,作用在小球上的合力为零,位置O 即为平衡位置。 若把小球从平衡位置略微移开后放手, 重物就在平衡位置附近往复地运动,这一振动系统叫做单摆[2]。
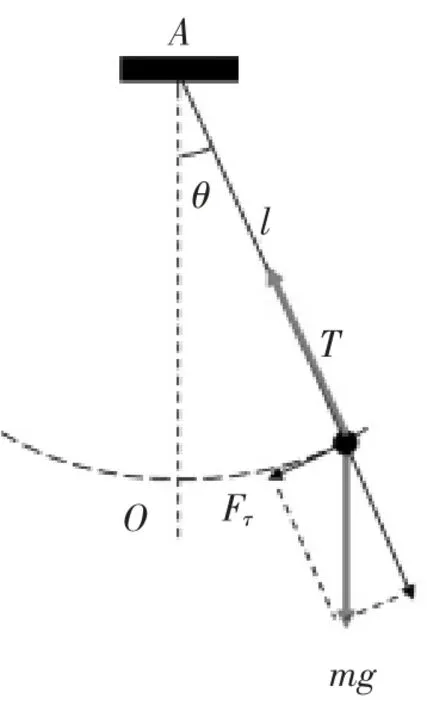
图1 单摆受力分析Fig.1 Force analysis of single pendulum
设在某一时刻, 单摆摆线偏离铅垂线的角位移为θ,摆锤的运动方程为式(1)。

根据简谐振动的特征, 简谐运动的方程为式(3),振动周期用式(4)计算。

由式(4)可以看出,在小角振动的情况下,单摆的周期与角振幅无关,这称为单摆的等时性。


由式(13)可知,实验中只需测量出摆长和周期,就可计算出当地的重力加速度g0。 实验装置如图2所示。
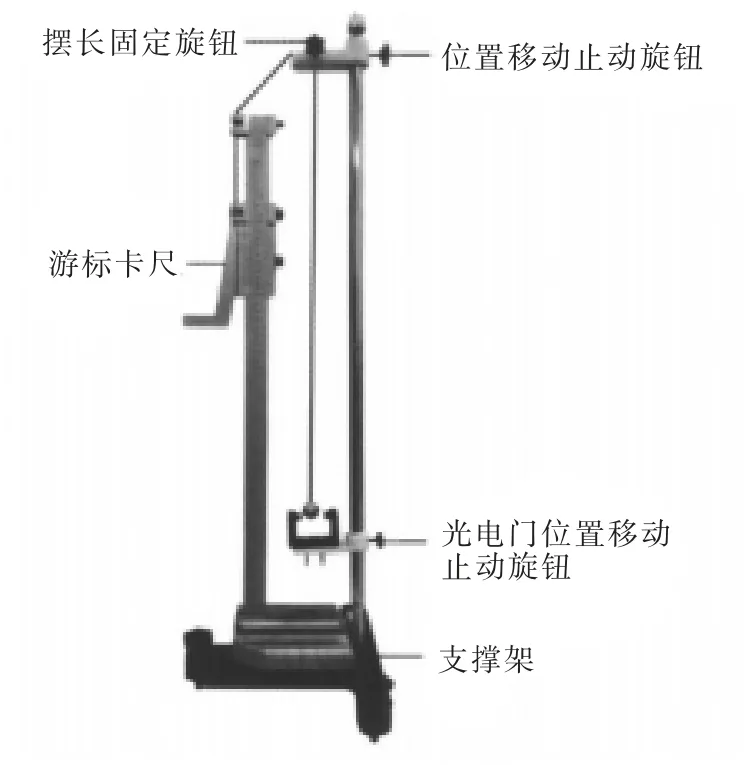
图2 单摆测重力加速度的实验装置Fig.2 Experiment device of gravity acceleration of single pendulum
1.2 实验数据处理的数学模型
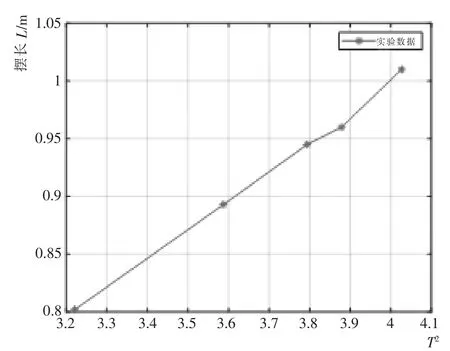
由式(13)可知,小角度平面单摆的摆长L 与振动周期T 的平方呈线性关系[3]。实验时,用米尺测量摆长L, 用秒表测摆动30 个周期用时t (分别测3次),计算摆动周期T。首先对实验数据进行预处理,详见表1。 根据表1 中的数据画出摆长与周期平方的散点图,如图3 所示。观察L 和T2的相关关系,发现各点基本在一条直线上, 这就可以通过线性回归来计算重力加速度。
一元线性拟合模型为:已知(xi,yi)(i=1,2,…,n)点大致在一条直线上, 则变量y 与x 存在y=β1x+β0的函数关系,其中β0和β1是未知待定常数,称为回归系数[4]。
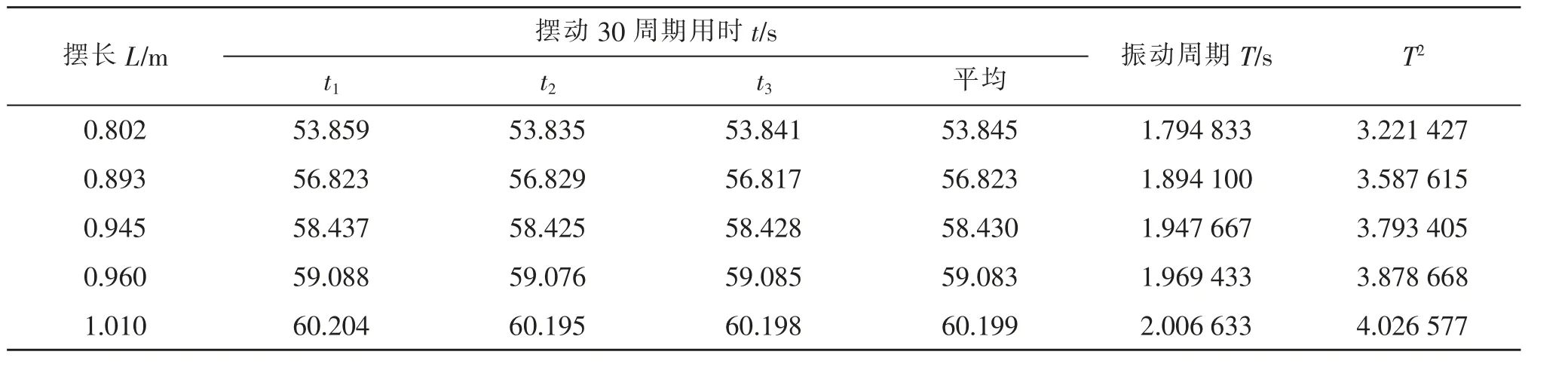
摆长L/m 摆动30 周期用时t/s 振动周期T/s T2 t1 t2 t3 平均0.802 53.859 53.835 53.841 53.845 1.794 833 3.221 427 0.893 56.823 56.829 56.817 56.823 1.894 100 3.587 615 0.945 58.437 58.425 58.428 58.430 1.947 667 3.793 405 0.960 59.088 59.076 59.085 59.083 1.969 433 3.878 668 1.010 60.204 60.195 60.198 60.199 2.006 633 4.026 577
根据拟合数据点(xi,yi)(i=1,2,…,n),确定一组拟合系数βk(k=0,1),使得如式(14)所示的函数达到最小值。

将实验记录数据用Matlab 作线性拟合(如图4所示), 可得函数表达式为L=0.252 9T2-0.014 088。根据直线的斜率,计算出重力加速度g=9.984 1 m/s2。
2 设计数据处理的GUI
MATLAB 提供了快捷的GUI 开发平台,提供了一套创建图形窗口的工具, 方便用户编程和再次开发[5]。在实验教学中,为了让学生把注意力集中到对单摆测重力加速度的实验原理的理解上, 提高学生分析问题和解决问题的能力, 就应尽可能减少数据的计算过程,从而达到最佳教学效果。
2.1 控件的布置与构思
根据实验目的和实验测量数据, 构思界面布局框架[6]。 本研究建立3 个坐标轴对象,分别用于显示实验装置、单摆动画演示和计算结果分析;4 个动作按钮,分别用来计算单摆周期、线性回归、实验数据清零和程序结束;相应控件的提示用13 个静态文本标签;测量数据的输入和计算结果的输出用33 个可编辑文本框来实现,设计布局如图5 所示。
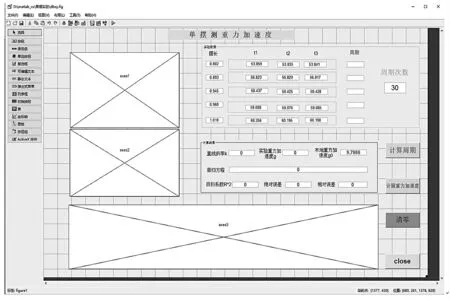
图5 GUI 界面设计布局Fig.5 Layout of GUI interface design
2.2 编写代码,实现控件的功能
在每个动作按钮回调函数中, 编写相应的代码程序,实现数据读取、变量的赋值、数据计算、计算结果输出、动态绘图等工作。 运行后,得到如图6 所示的GUI 初始界面和单摆的仿真动画。
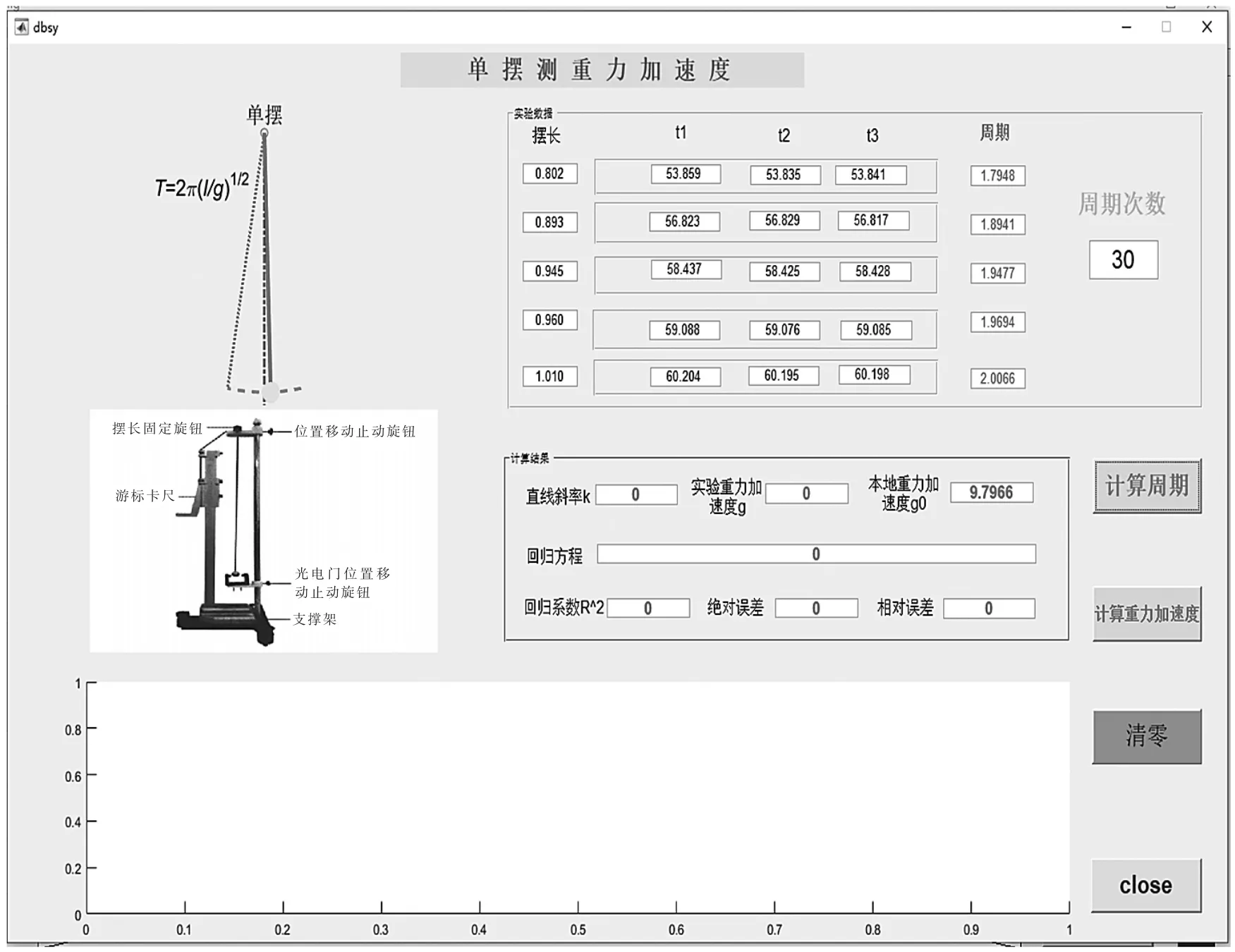
图6 GUI 界面运行初始Fig.6 Beginning of GUI interface running
3 实验数据处理可视化演示
在相应的文本框中输入每次实验的摆长、时间、周期次数、本地重力加速度等实验数据后,单击“计算周期”按钮,可计算出不同摆长所对应的周期,在此基础上,点击“计算重力加速度”动作按钮,可得到回归方程为:L=0.249 11T2, 同时计算出重力加速度和误差,并将其显示在对应的文本框中,具体的计算结果如表2 所示。在图形窗口上,画出回归直线和残差分析,如图7 所示。
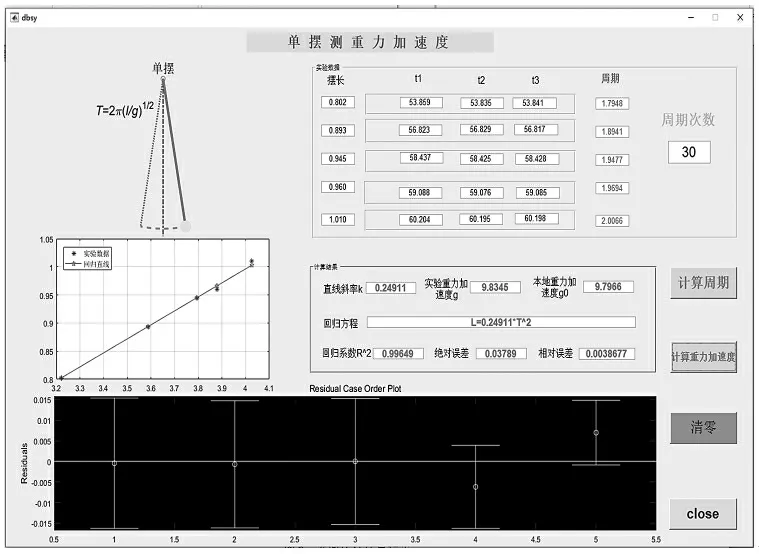
图7 界面运行计算结果Fig.7 Calculation results of interface running
用户运行GUI 后,通过观察回归直线与残差分析,可以判断实验数据的准确性[7]。 如图8 所示,当实验数据出现异常时, 系统从两处通过图示给出了警示,从而可以方便快捷地找出异常数据。

测量次数 摆长L/m 周期T/s 直线斜率 实验重力加速度/(m/s2) 本地重力加速度g0/(m/s2) 相对误差/%1 0.802 1.794 8 2 0.893 1.894 1 3 0.945 1.947 7 4 0.960 1.969 4 5 1.010 2.006 6 0.249 11 9.834 5 9.796 6 0.386 87
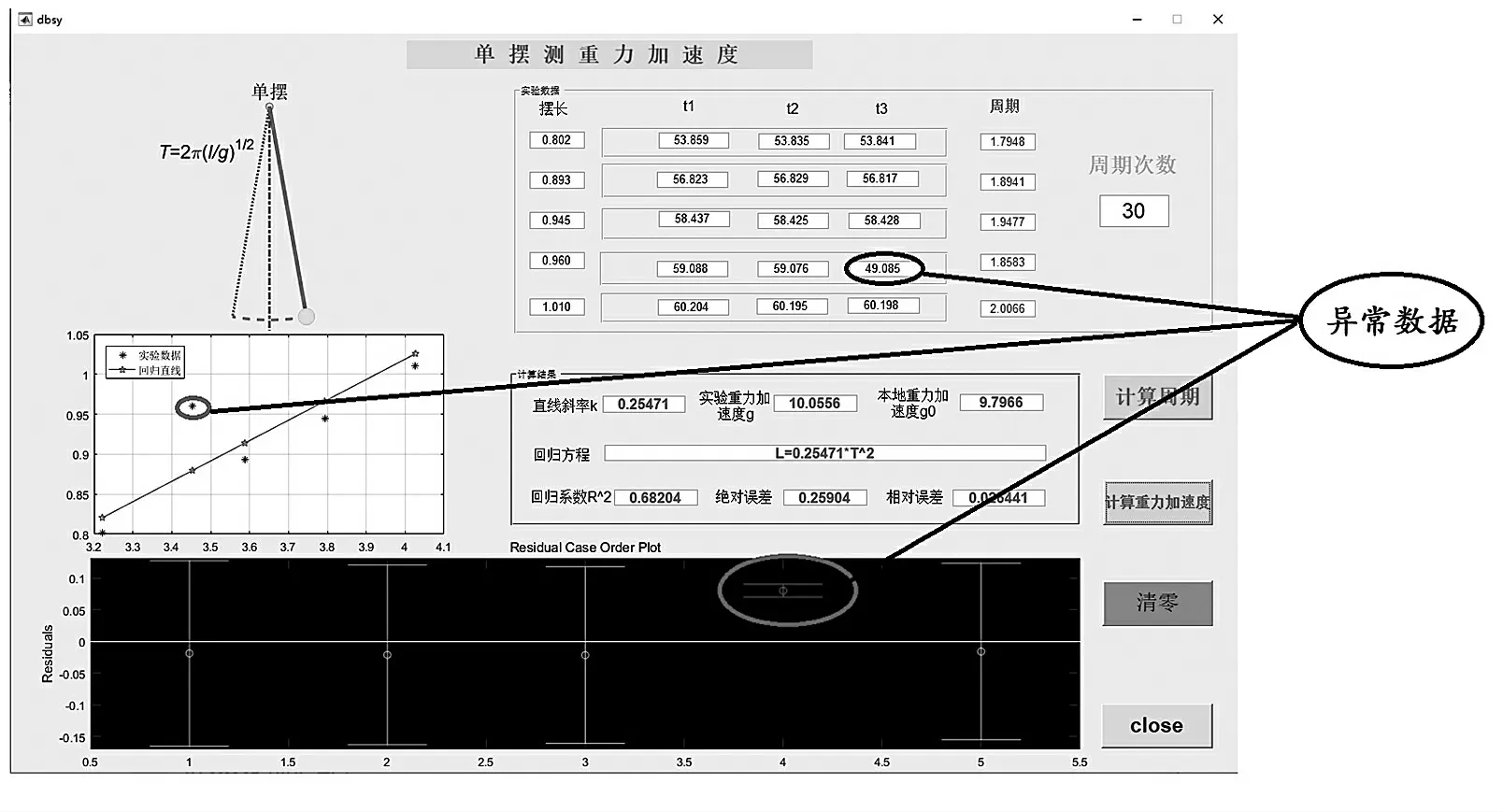
图8 出现异常数据Fig.8 Abnormal data
在每次对实验数据进行处理时, 只需把实验数据输入到相应的文本框中, 单击相应按钮就可实现求解,并进行数据可视化,实现了人机交互的功能。
4 结语
基于Matlab 软件设计的单摆测重力加速度实验数据处理的可视化系统,通过GUI 界面设计和自行设置参数,实现了数据的可视化,减少了重复计算过程,节省了大量的时间,并且能及时检验实验数据的准确性,提高了实验精度,实验效率也大大提高。该系统界面友好,设计简洁明了,并可再次开发,便于推广。 在教学中可以鼓励学生自行设计与开发GUI,激发学生探索、创新的勇气和热情。

