房地产市场定位产品组合策略研究
廖苏宏
(江西财经大学 旅游与城市管理学院,江西 南昌 330013)
在房地产市场开发领域,随着开发技术的日益成熟,竞争日趋激烈,因此开发前期的房地产策划应运而生,涉及开发产品的市场接受度,并最终影响到销售收入。
在房地产策划中,包括前期策划和后期执行,其中产品策划就是前期策划中的重要内容。在产品策划各项内容中,涉及产品形象的把握、概念的提取、形态的构成、产品的组合等。由于产品的组合考虑方面较多,需要与规划、设计、市场部门进行大量的沟通、协商与配合,因此,产品组合相较于其他内容的策划就更为复杂和重要。
所谓产品组合是在一个项目开发建设中不同物业类型的组合、同一物业类型中不同户型(包括同一户型不同面积段)组合。①文章暂且仅讨论商品房住宅领域,暂不考虑商场、酒店、写字楼等物业。它一般有两个主要指标:物业类型和户型。物业类型,有类别墅、联排别墅、叠拼别墅、洋房、高层等;而户型既包括一居室、二居室、三居室、四居室、跃层等,也包括不同面积段的同一户型,比如从75m2到125m2的二居室。产品组合有两种,第一种是全线全面型,这种类型是指通过增加产品类型来获取更多类型的客户,完善项目的产品组合的关联性,包括项目类型、各类型的面积段、户型等;第二种是产品专一型,这种类型是指不依靠产品种类的多样化寻求客户范围,二是专业化开发某一种市场上的产品,不注重各产品之间的关系,这类特征受城市位置和所形成的相应物业聚集度的影响,比如在居民集中区只开发高层。
房地产产品组合越丰富,比如既有类别墅,又有洋房、高层等,既有75m2的二居室或三居室,又可以有90m2、100m2、125m2不等的二居室或三居室等各类户型或面积段的产品。产品线越丰富,消费者的可选空间就越大,越能满足不同客户的需求,这样就能降低项目的风险度,但是产品组合不是越多越好,它受总面积、容积率、生产经营成本、销售进度等因素的影响。因此合理的产品组合就变得至关重要。然而,在产品组合中,变量较多、不易把握,“牵一发而动全身”,房地产策划人员通常依靠其直觉和经验,反复试算,判断哪类产品组合才能实现价值最大化。显然,不具科学性,精确度难以保证。
房地产开发追求以合理的投入获得较大的产出,对于具体的开发项目而言,采用定性分析的手段是非常重要的,另外,在定性分析的基础上,还需结合数量指标和数学模型进行定量的分析和计算,以此来获得项目的最优解决方案,进而对企业决策进行指导。定量分析手段的应用,使用范围较广的是运筹学,其中主要采用的是数学规划的方法,数学规划中与安排和估值相关的内容,能够解决现实中的很多问题。比如在一定条件下,按照某一指标的某种标准寻求最佳的规划方案。①周玲:《产品组合规划在房地产开发中的应用——利用定量分析解决最优产品组合问题》,《改革与开放》2011年第6期,第139、141页。对此,利用线性规划的数学模型分析产品组合的优化可以表示成求解目标函数在满足约束条件下的极值问题。因此本文将项目价值最大化即价格作为目标,以类别墅、联排别墅和高层为产品的物业类型,依据给定的规划条件(一定的占地面积和总容积率)为前提,借助运筹学,通过建立线性回归方程,求解出最优组合的物业类型及其面积段。
一、相关文献回顾
对房地产项目产品组合的研究文献较少,安玉华、陈小龙研究认为,首先假设项目具有可行性、预期收益和经营模式服从正态分布、资源不受约束等条件,然后约束了投资变量形式、规模、最低投资、开发周期,然后引入风险系数和所承担的风险达到的最低水平,在此基础上建立了目标函数公式。接着进一步设置普通住宅、高层住宅、底层商业用房为变量,由此可知有8种的可能组合,根据已知的容积率确定了最大建筑面积。综合考虑市场的情况下,可以推出高层和普通住宅面积的需求区间及收益值。利用单纯形法计算,求出最优解,得到了普通住宅、高层住宅、地上的建筑面积,在此情况下可实现最大收益。但是本文中所涉及的数学模型和最优产品组合求解办法,仅适应于中小型房地产企业进行开发决策,对于大型房地产企业或大规模项目不适用。②安玉华、陈小龙:《对我国中小型房地产企业的投资优化组合模型探究》,《门窗》2016年第3期,第206、208页。
姚学群在文章中首先也做了假定:房地产开发企业以利润最大化为目标、只受到市场需求和城市规划及地块规划条件的限制,不受到诸如能源和劳动力等资源的约束限制。接下来,作者将可投资资本、城市及本地块的规划、经调查取得的市场需求等相关因素作为约束条件,将产品组合收益最大化作为目标值,就得到了上述约束条件与产品组合收益最大化之间的函数。最后作者通过一定的方法将非线性问题转变成线性规划问题。本文还对该模型在实际生活中的应用进行分析,对产品的多种组合用数学规划的方式给出了利益最大化的结果。③姚学群:《房地产开发项目投资决策定量方法研究》,昆明理工大学2007年硕士学位论文。
张媛、于国钧认为数学规划的手段对于房地产项目开发决策具有非常重要的意义,它能够解决产品规划中的产品组合问题。但作者认为,目前数学规划在产品组合决策中的应用,只能够解决某一指标最大化作为目标函数,考虑的角度较为单一④张媛、于国钧:《基于动态分析的房地产开发投资组合决策规划模型研究》,《工程管理学报》2014年第1 期,第123—127页。,是一种静态的投资组合决策方法,没有考虑到市场的实际需求、市场接受度,尤其没有充分考虑到企业资金运用的时间价值,在这种情况下得到的收益并不一定能实现企业利润最大化,也就是说此时的产品组合并非为最佳结果。实际上在项目操作过程中,还应该考虑资金的时间价值,动态考虑投资效益。所谓计算企业的资金时间价值,其中包含现值计算和终值计算,是在不考虑风险及通货膨胀的条件下(因此这是一个相对数,主要用社会平均资金报酬率表示,也是企业资金的最低成本率),进行两种资金价值的计算,根据不同时期项目需求不同导致的资金流动,按照一定的折现率将其转换为同一时期的资金价值,能够对不同时间点的投资收益进行分析。经等额换算的方式折算到同一时间点上。作者强调,这种动态的决策分析方法,相比传统静态分析,更符合客观事实,是更加科学和精确的投资决策分析方法。文章最后谈到,基于动态分析的房地产开发投资组合规划决策模型与传统决策模型相比能更精确地计算出项目实际投资利润的理论最大值,客观反映市场的实际情况并充分体现资金的时间价值,在决策中可以帮助企业真正达到指引项目利润最大化的目标。另一方面,我们也应注意到,通过该方案求得的各类产品的建筑面积只是理论建议值,最终还应经过设计院的强排验算,才能最终确定实际规划建筑面积、类型组合和相应的户型产品配比。
周玲表示,在定量分析中使用较为普遍的数学规划,主要用来解决在一定的规划限制条件下,寻求某一指标最优化的解决方案,可以理解为在约束条件下满足极大值或极小值的问题。房地产开发受到市场环境(包块政策、经济)、项目所处地段、城市规划及项目本身规划、可投入的资金等诸因素的影响,在满足各方要求的条件下,运用线性规划方式,在资金投入有限的情况下,寻求经济效益最大化,也可以说是如何寻找房地产项目最优产品配置的方式。在文中作者以类别墅、双拼别墅、联排别墅、叠加、多层的一般容积率、平均建造成本、目标样本调研比例、预售价、用地毛利率数据为研究对象,通过建立优化模型,在各类型建筑占地面积约束、总土地面积约束、容积率约束下求得最大价值下的各个物业类型的终值。①周玲:《产品组合规划在房地产开发中的应用——利用定量分析解决最优产品组合问题》,《改革与开放》2011年第6期,第139、141页。
简彩云并不赞成通过传统的模拟线性关系的方法来做产品投资组合的分析,认为该方法较为简单,有非理性之处,很大程度上带来不符合市场需求的错误决策,在多类型或房地产市场价格动荡不稳时,上述情况就表现得更为明显。文章基于房地产投资收益影响因素的研究,引入数学规划手段,在研究房地产投资决策时引入价格变化、建筑成本变化及费用变化三项变量,丰富了房地产投资决策模型影响因素,构建了房地产投资决策的非线性模型,并结合现实项目数据进行模型验证,证明该方法在现实中应用是可靠且有效的。②简彩云:《基于动态规划的房地产投资决策模型构建》,《决策参考》2010年第17期,第51—54页。
二、数据处理与方程
(一)数据来源与筛选
本文选取的数据来源于福建省武夷山市一旅游商业开发项目:“武夷·紫阳古城”。紫阳古城项目又名“武夷·山水名城”,位于武夷山旅游景区内,开发单位为华泰地产,致力于打造国内优秀的情景民俗文化体验古城。当地政府对该项目十分重视,将其定位为武夷山首个集中式商业文化古城。项目在设计上充分借鉴国内优秀的古街、古镇案例,既保留原有的文化韵味,又增加了现代化体验元素,通过商业风情街区打造,带动区域商业氛围,打造集旅游度假、文化演出、商业休闲于一体的复合型商业街区。
项目地理位置(见图1):本项目位于武夷山国家旅游度假区内,地处武夷大道东侧,北临梅溪水系形成的碧湖园,南靠狮子山,西临武夷大道主干道,东为在建的角亭民俗文化村。距武夷山风景高尔夫度假酒店(五星级)约200 米,至火车站约9 公里,至飞机场约4.5 公里,至市区约为10 公里,至度假区中心约1.5 公里,至景区主入口约2公里;至在建的宁武高速公路入口约0.8公里;交通非常便利。
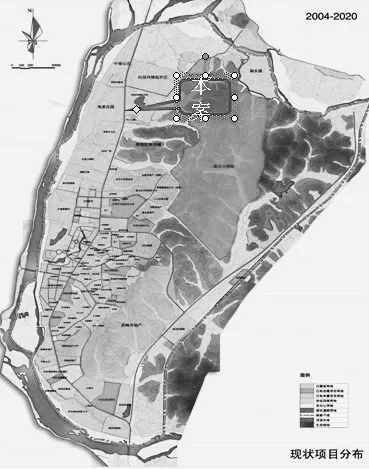
图1 武夷山项目位置图
项目基础经济技术指标(见表1):

表1 项目基础经济技术指标
本项目所在区域位于三姑国家旅游度假区北部,周边项目有“九龙湾”“风景高尔夫度假酒店(五星级酒店)”“武夷水庄”等大型房地产楼盘。项目定价以上述项目作为对比,通过对地理位置、交通便捷度、项目配套完善程度、项目规模、产品素质、赠送面积、项目附加值等参数进行比对,根据与本项目综合素质近似程度确定细项权重,分别得出项目各物业销售均价(见表2):

表2 各物业类型市场均价①表1及表2数据来源于福建省“武夷·紫阳古城”旅游商业开发项目及经过市调当地房地产市场数据。
其中,高层产品因产品间(以建筑面积区分)素质差距较大,售价有较大差别,通过对面积大小、户型结构、业态分布、通风与采光、沿街情况、楼栋密集度、朝向、景观与视野、环境与噪音等因素进行综合比较,得出不同高层产品面积如表3:

表3 各高层产品段市场均价
(二)模型与变量选取
本文为建立线性规划求解方程,需要对以下变量进行选取。
首先,作为房地产开发项目,我们应该明确开发目标,目前对项目营销目标的理解,通常意义上只有三种情况:一是价格目标,二是销售速度目标,三是品牌目标。其中排除品牌目标,这不在本文讨论范围之内。因为品牌目标本身无法建立量化方程,不是数理经济讨论的范畴。
其次,销售速度目标虽然和销售价格息息相关,但同时考虑价格和速度两个目标,需要同时结合企业战略进行研究,本文暂不考虑。因此本文只进行价格目标的研究。这样,我们就把问题简化为进行价值最大化(MAX Z)的目标函数关系。
接下来,我们来研究项目价值最大化情况下的影响因素和约束条件。首先来看影响因素。影响价格高低,主要取决于物业类型。目前市场上按价格由高到低的物业类型分别是类别墅、联排别墅、叠拼别墅、洋房和高层。经过市场调查,在武夷山市场上叠拼别墅和洋房产品接受程度低,本案不建议建设。这样,我们就需对类别墅(建筑面积X1)、联排别墅(建筑面积X2)和高层(建筑面积X3)三种产品组合进行基于价值最优的规划求解。
在得到三种产品组合之后,由于各类产品的内部组合又相对复杂,我们需要对各类产品的面积段做进一步的产品组合规划求解。同样依据市场调查数据,目前市场上主流别墅产品和洋房产品均较为单一,主流面积较为集中,不再做进一步的规划求解。高层产品相对分散,主流套均面积为130 m2(套数X31)、160 m2(套数X32)和200 m2(套数X33)。我们对以上三类产品组合作进一步的规划求解可得到最终具体的包含面积段的产品组合。这样便可以用于指导具体的规划设计任务了。
(三)建立线性规划方程
首先,我们通过市场调查已得知,类别墅、联排别墅和高层的市场均价为12000元/m2、9000元/m2和8000元/m2。由此我们可以建立目标函数方程
Max Z1=12000×X1+9000×X2+8000×X3
同时,我们依据地块给定的规划条件,地块总面积为733.363亩,总容积率不大于1.2,根据规划设计常识已知,类别墅、联排别墅和高层的规划容积率分别为0.3、0.6 和2.0。于是我们可以得到如下约束方程
S.t.
X1+ X2+ X3≤733.363×666.67×1.2
X1/0.3+ X2/0.6+ X3/2 ≤733.363×666.67×0.3
通过以上规划求解方程计算,得到以下计算结果

接下来,我们进一步对高层产品进行细分。通过市场调查得知,200 m2、60 m2、130 m2产品的市场均价分别为8500元/m2、8000元/m2和7800元/m2。综合不同产品类型,我们可以建立类别墅、联排别墅和不同面积的高层产品的价值最大化目标函数方程
Max Z2=12000×X1+9000×X2+8500×200×X31+8000×160×X32+7800×130×X33
同时,依据波士顿矩阵对产品进行的功能定位以及营销部门给定的条件,200 m2的产品作为高层产品中正向价值标杆的明星产品,比例不低于5%;160 m2的产品作为现金牛主力产品,比例不得低于40%;130 m2的产品作为小户型保证走量,比例不得低于15%,作为共同的现金牛产品,130 m2和160 m2产品之和不得低于60%。由于各种户型产品不可能出现小数点,因此设定取整。我们可以得到如下约束方程
S.t.
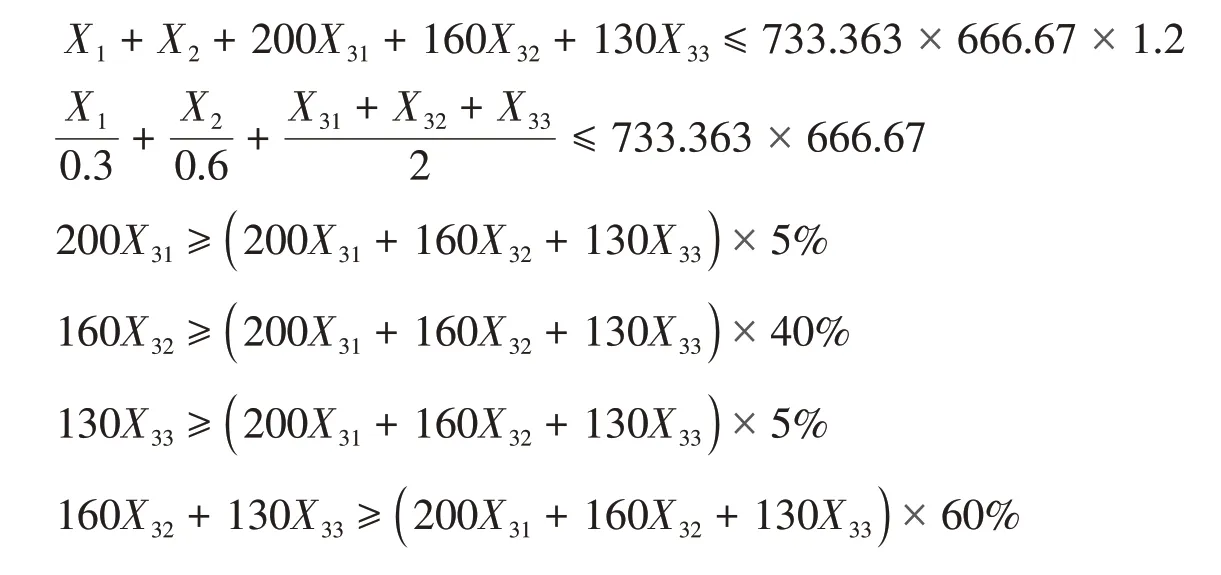
Xi=int(i=1,2,31,32,33)
通过以上规划求解方程计算,得到以下计算结果
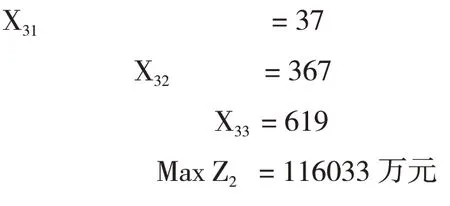
三、最优结果与分析
按照以上线性规划方程求解结果,我们可以得到如下产品组合(见表4):

表4 产品组合详表
按照这个产品组合,对应的总价值(见表5):

表5 规划求解后的价值总量表
在这一组产品组合中,我们得到了一组最优解,包括最大价值总量和对应的产品组合。理论上说,这样一组产品组合是可以指导设计进行具体的规划设计工作。但其中有两个细节值得讨论。
(一)总价值量从第一次规划求解的557358 万元到第二次规划求解的556052 万元,少了1306 万元,即
△1=Z3-Z1=557358-556052=1306万元
从技术的角度上说,这是一个技术瑕疵,因为对各物业类型的产品做进一步的最优规划求解之后,其产品组合的平均价格与原物业类型市场平均价格不符,进而要求我们回去对第一步产品的规划求解再代入第二个平均值后重新求解,之后的第二步也再重新做一遍,在多轮最优求解之后,最后△值趋近于0,过程如图2。本文不对如上过程做进一步的求解。一是基于本文的主要目的是使用规划求解工具解决产品组合规划问题,使用技术手段替代之前的经验判断。二是△在产品组合后的总价值中占比很低,

图2 多次回归结果的渐进过程
△1/MAX Z1=1306/556052×100%=0.23%
那样即使做很多轮对产品组合的优化也十分有限,敏感度极低。
(二)就是已知条件中,我们需要对市场平均价格进行必要的说明。因为房地产市场是个典型不完全市场,其中价格随着区位和产品的变化非常大。因此对于市场均价理论上应该是经过比准修正的比准价格,而不是直接从市场中得到的市场均价。论证过程并非本文讨论的范围,读者知晓便可,在此从略。
(三)如果使用传统手动试算,很难对多个因素的取值进行精确计算。在本案中,由于手动试算一般按每5%进行上下调节,最大可能的产品组合(见表6):
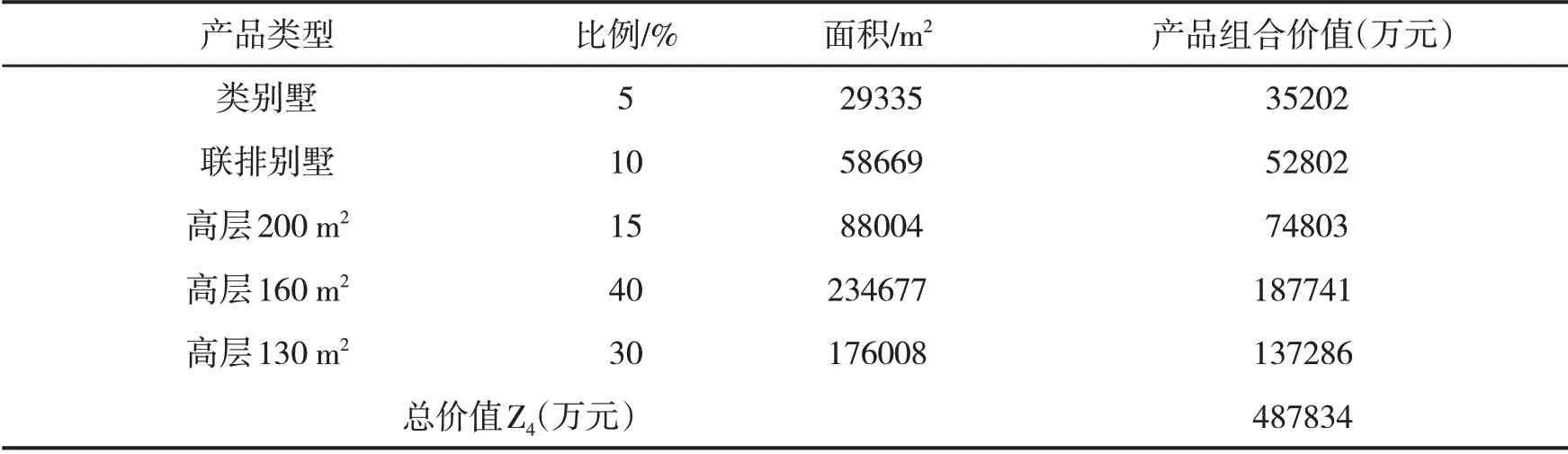
表6 手动试算情况下可能的比例、面积、价值总量表
这个计算结果的总价值与最优结果之间差异非常大
△2=Z4-Z1=487834-556052=-68218万元
偏差率为
△2/MAX Z1=-68218/556052×100%=-12.26%
四、结论与启示
通过本文的研究,我们从项目实证的角度,证明了最优规划求解在房地产产品组合中能发挥重要的数理经济学作用。在本案的实际操作中亦是如此,投资人借助顾问机构得到此结论之后,迅速指导规划设计院进行方案设计,最终项目也在市场当中获得了良好的经济效益。对此,我们至少可以得到如下结论和启示:
(一)借助规划求解方法,能够迅速解决在产品组合规划中遇到的不科学问题,使该问题的解决朝着数理化、逻辑化方向发展,便于管理者迅速做出开发决策。
(二)该方法的普及,有利于投资人今后在取地策略研究中进行项目价值最大化的估算,为投资决策提供有力的数学基础。如果使用传统手动试算,我们可以发现,偏差率为-12.26%,即使是经验十分丰富的策划人员,要将这个偏差率降到10%以内,也是一件工作量巨大、难度非常大的工作,甚至可以说无法完成。
(三)房地产经济学的理论化建议水平目前还相对较低,不断借助工具提高我们的研究能力和管理水平是我们地产人共同努力的方向。
(四)由于我们的决策数据是建立在数理分析基础之上的,为我们今后在项目风险管理中的各项指标分析提供了理论支持。
(五)由于房地产开发是个长期动态的过程,尤其是大型房地产开发项目,在分期开发过程中,分期动态调整产品组合是一项重要任务,借助规划求解工具,我们才可以快速进行产品组合规划和经济分析,找到正确的开发方向。
(六)由于规划求解工具在这一领域的成功运用,我们可以在今后房地产开发中的土地一级开发、城市产业定位方向上也进行尝试,并在实践过程中不断验证方法的有效性和科学性。让房地产相关领域的研究更加科学化、规范化。

