胶凝砂砾石材料抗冻性研究及配合比优化设计

师现营，李晓南，陈平平

（1.河南省豫东水利工程管理局，河南 开封 475000；2.河南省豫北水利工程管理局，河南 新乡 453000；3.华北水利水电大学 水利学院，河南 郑州 450046）

胶凝砂砾石作为一种新型筑坝材料，由少量的胶凝材料和不经水洗、筛分的砂砾石料通过简易拌和而成。目前，已有相关专家对胶凝砂砾石材料筑坝形式、结构设计、力学性能、本构模型等进行了系统研究，为该材料的设计及应用提供了理论基础［1-6］。位于严寒地区的胶凝砂砾石坝，冻融破坏是威胁其安全的主要因素。刘红森等［7］研究了影响胶凝砂砾石抗冻性的敏感因素，结果表明，随着水泥和粉煤灰掺量的增加，水胶比和砂率降低，胶凝砂砾石的抗冻性显著提高；赖韩等［8］研究了用水量、单位水泥用量、单位粉煤灰用量和砂率等四因素协同作用对胶凝砂砾石材料性能的影响，认为用水量和粉煤灰用量是影响材料综合性能的主要因素；闫林等［9-10］对胶凝砂砾石材料的配合比进行优化设计，认为确定合理的胶凝材料用量和水胶比是设计关键。可见，确定最优水胶比、砂率和胶凝材料用量是胶凝砂砾石材料配合比设计的核心，明确各因素对胶凝砂砾石材料抗冻性的影响规律，对提升该材料的抗冻性具有重要的意义。响应面分析法是解决多因素问题的有效方法，利用回归方程拟合因子与响应之间的函数关系，对回归方程进行分析，预测其最优参数组合，已逐渐被引入工程材料研究领域［11-12］。陈守开等［13］应用响应面法分析了三因素及其交互作用对胶凝砂砾石力学性能的影响，认为采用响应面法建立的多元回归模型较为精确。

本文采用响应面法，选取水胶比、砂率和粉煤灰掺量3个因素，研究三因素对胶凝砂砾石材料抗冻性能的影响规律，建立回归模型，并通过多重响应分析，对胶凝砂砾石配合比设计提出优化建议。

1 试验概况

1.1 原材料

粗骨料为许昌周边河床砂砾石，采用二级配骨料（中石子∶小石子=3∶2），其中中石子粒径为20～40 mm，小石子粒径为5～20 mm，堆积密度为1 669.3 kg／m3；天然河砂购自唐河县鑫淼砂石有限公司，细度模数为2.94，堆积密度为1 625.0 kg／m3，含泥量为1.5%；水泥为普通硅酸盐水泥（P·O42.5），力学指标见表1；粉煤灰购自河南豫联电厂，Ⅰ级灰，其物理／化学特性见表2；拌和用水为郑州市自来水。

表1 水泥力学指标

表2 粉煤灰物理／化学特性

1.2 试验方法

胶凝砂砾石试件尺寸为100 mm×100 mm×400 mm。试件成型方式为搅拌、插捣、振动成型，试件在成型过程中通过湿筛法剔除粒径大于31.5 mm的骨料。试件标准养护28 d。

选用苏州东华仪器有限公司的HDK-9混凝土快速冻融试验机作为快速冻融试验设备。试验机可通过计算机自动控制试验过程，根据试验方案确定冻融循环次数，达到设定次数后对试件进行性能测试。选取冻融循环25次后试件的质量损失率和相对动弹性模量作为分析指标［14］。

1.3 试验设计及试验结果

以水泥用量50 kg／m3的胶凝砂砾石材料为设计基础，对水胶比（A）、砂率（B）和粉煤灰掺量（C）3个因素设计3个水平，见表3。利用Design-Expert软件，选择Box-Behnken工具设计三因素三水平二响应试验，共17组试验（见表4），为了更清楚分析多种因素交互作用，其中析因部分试验12组，中心重复试验5组（组号为5、6、7、8、11）。试验结果见表4。

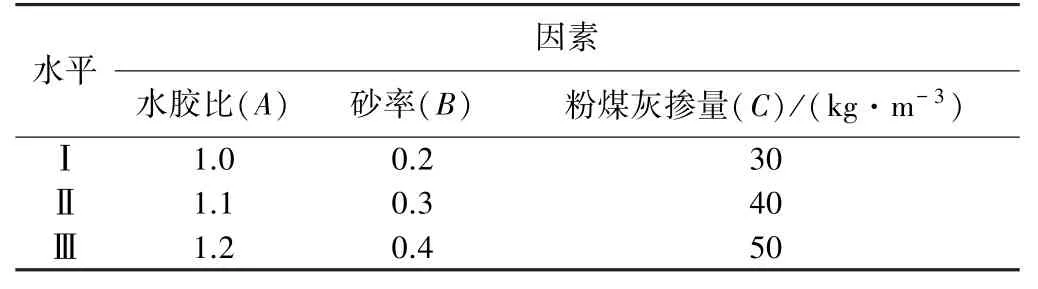
表3 因素水平设计

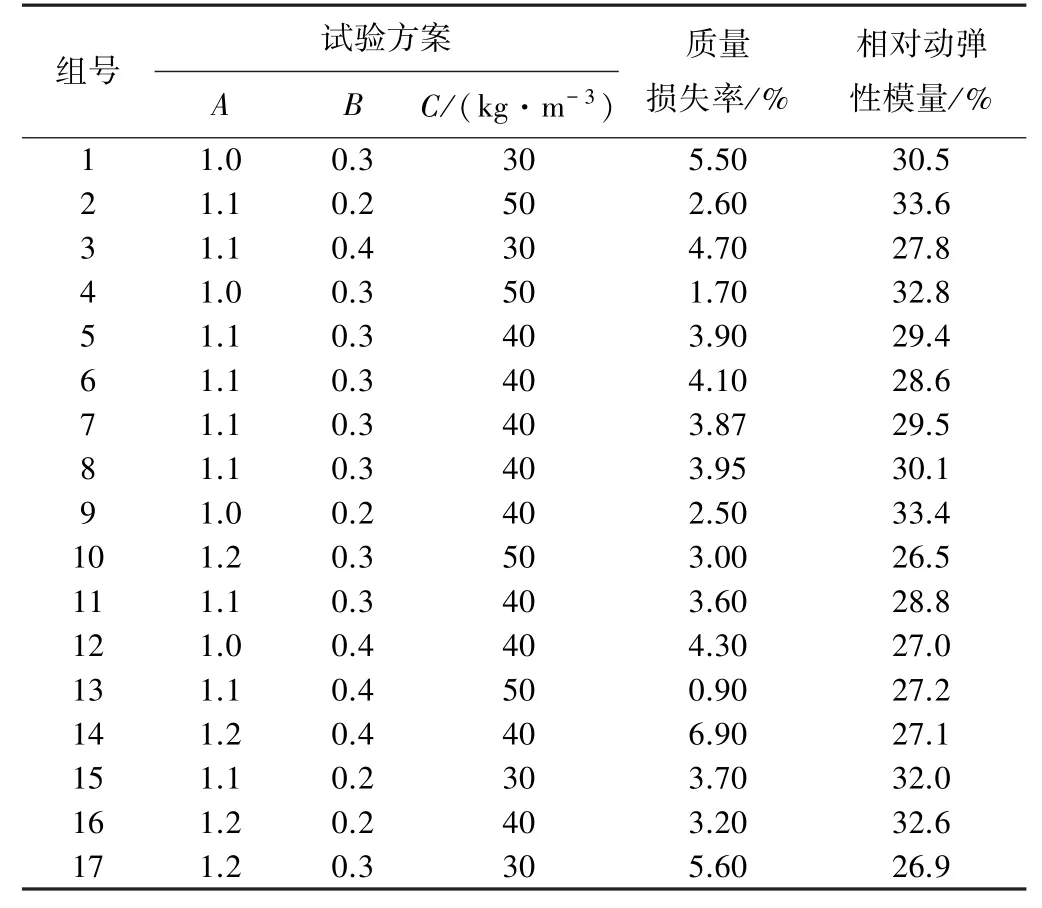
表4 试验方案及试验结果

2 响应面模型

2.1 模型的构建与分析

选择Quadratic模型进行方差分析，去除失拟项，建立关于A、B、C、AB、BC、A2、C2的胶凝砂砾石冻融25次循环后的质量损失率（M）多元二次方程（模型）为

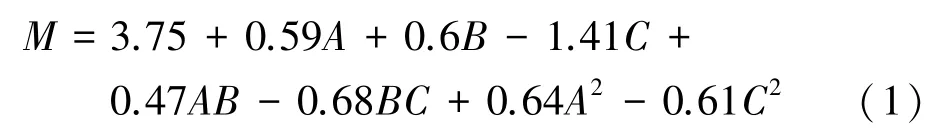
质量损失率模型显著性分析和统计分析结果见表5。

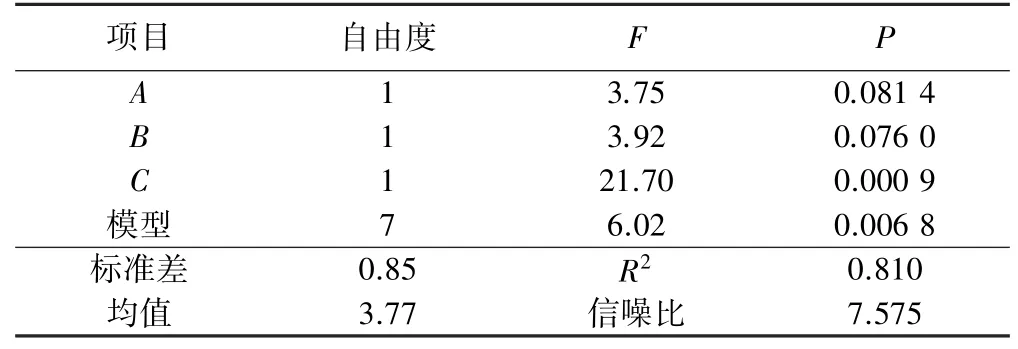
表5 质量损失率模型显著性分析和统计分析结果

由表5可知，该模型F=6.02，P=0.006 8＜0.050 0，表明该模型具有统计学意义；信噪比=7.575＞4，决定系数为0.810，说明该回归模型可靠性较强，试验误差较小。因此，可根据该回归模型进行多因素相关性分析以及预测未知因变量。其中单因素C的P值远小于0.05，说明粉煤灰掺量对质量损失率的影响极其显著，其次是B和A，根据P值，质量损失率影响因素的主次顺序为粉煤灰掺量、砂率、水胶比。

同理，建立关于A、B、C、AB、AC、BC、A2、B2的胶凝砂砾石材料冻融25次循环后的相对动弹性模量（E）多元二次方程（模型）为

相对动弹性模量模型显著性分析和统计分析结果见表6。

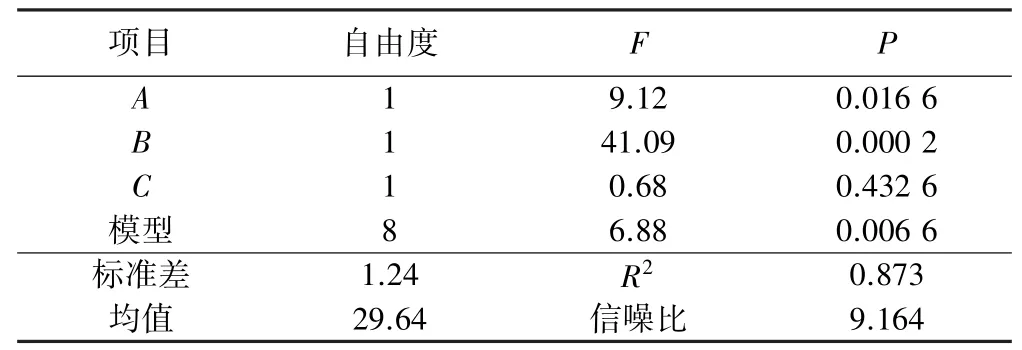
表6 相对动弹性模量模型显著性分析和统计分析结果

由表6可知，该模型F=6.88，P=0.006 6＜0.050，表明该模型具有统计学意义；信噪比为9.164＞4，决定系数为0.873，说明该回归模型可靠，误差小。因此，该回归模型可用于对测试结果进行相关分析和预测。其中，单因素A、B的P值远小于0.05，表明水胶比和砂率对相对动弹性模量的影响极为显著，C次之，根据P值，相对动弹性模量影响因素的主次顺序为砂率、水胶比、粉煤灰掺量。

2.2 响应面模型等值线图

响应面模型的等值线图可以直接反映各因素及其交互作用对响应值的影响程度，从而确定各因素的最佳取值范围。

图1～图3为双因素交互作用下冻融后质量损失率等值线图（以质量损失率最小时的双因素交互作用图进行说明）。分析单因素影响作用可知，水胶比增大时质量损失率逐渐增大，砂率和粉煤灰掺量增大时质量损失率减小，且在设计试验组范围内，水胶比为1.0、砂率为0.4、粉煤灰掺量为50 kg／m3时胶凝砂砾石冻融后质量损失率最小。分析双因素交互作用可知，水胶比与砂率交互作用下质量损失率变化范围为1.5%～3.0%，水胶比与粉煤灰掺量交互作用下质量损失率变化范围为2.0%～7.0%，砂率与粉煤灰掺量交互作用下质量损失率变化范围为2.0%～5.0%。说明，水胶比与粉煤灰掺量的交互作用对胶凝砂砾石冻融后质量损失率的影响最为显著。原因是当水泥用量固定时，胶凝材料用量取决于粉煤灰掺量，而能否保证胶凝材料充分水化取决于水胶比，在最优水胶比下，胶凝材料充分凝结水化，骨料之间黏结力增强，能够有效改善冻融后胶凝砂砾石表面剥蚀程度，减少胶凝砂砾石冻融后质量损失。

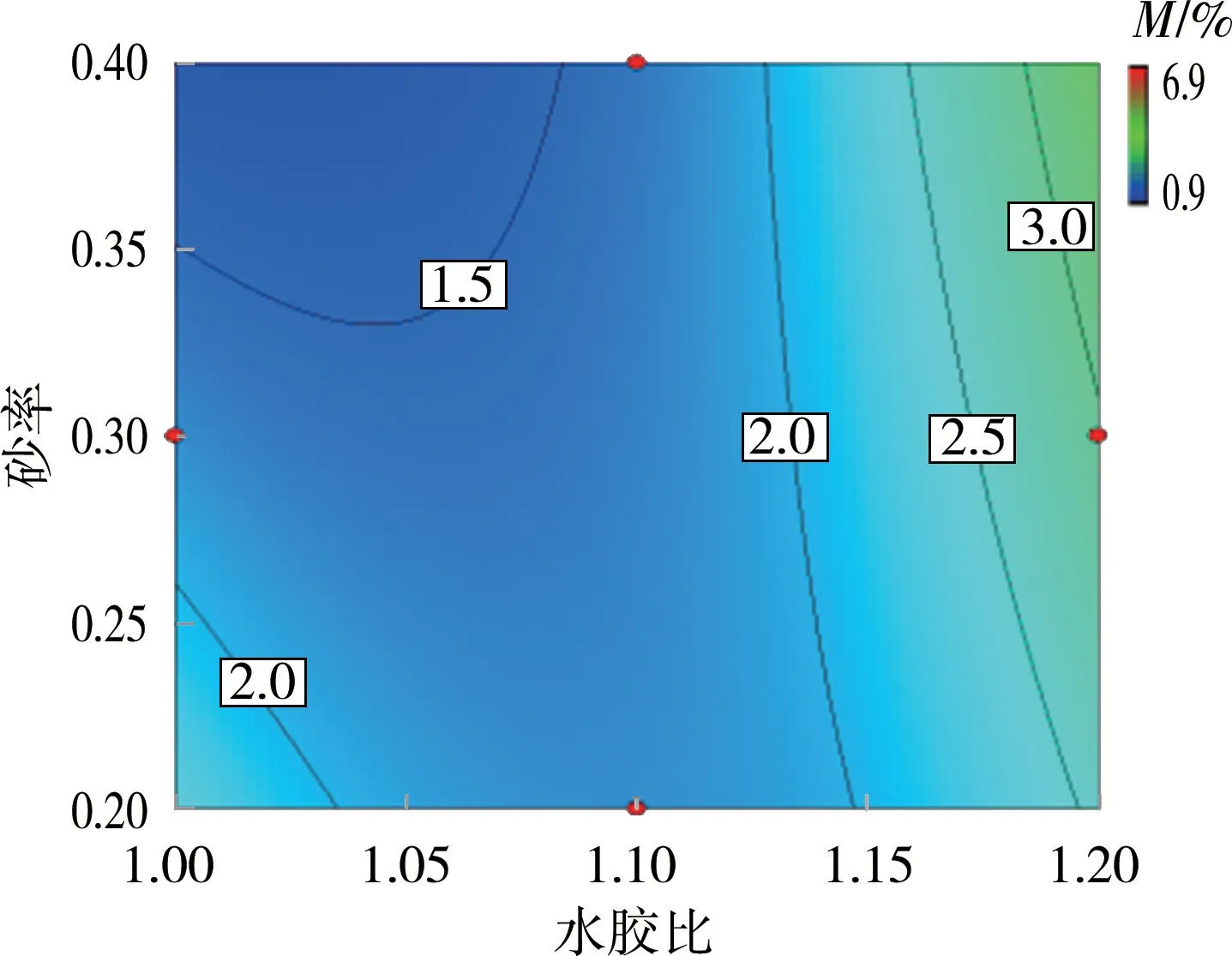
图1 水胶比与砂率交互作用下质量损失率等值线（粉煤灰掺量为50 kg／m3）

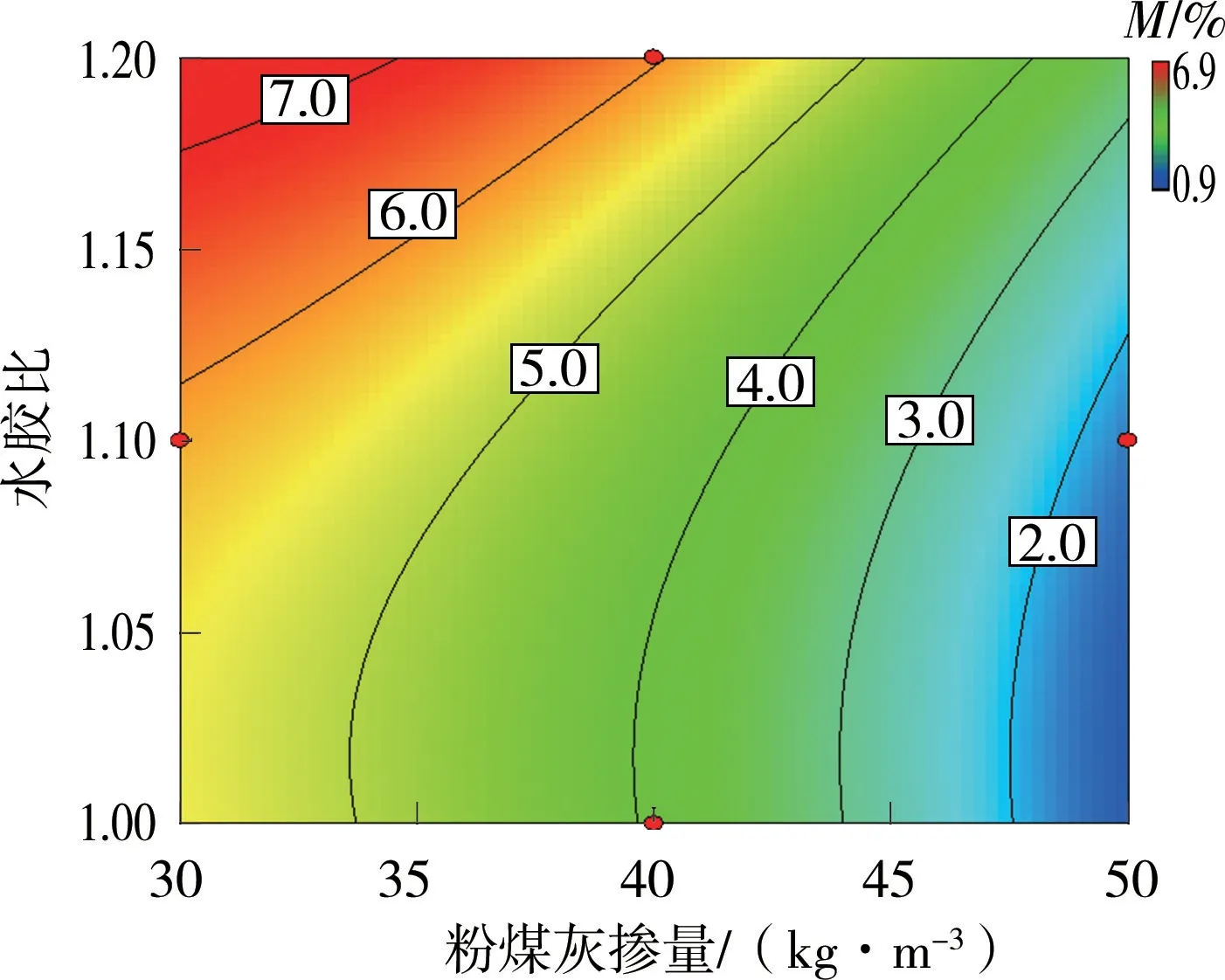
图2 水胶比与粉煤灰掺量交互作用下质量损失率等值线（砂率为0.4）

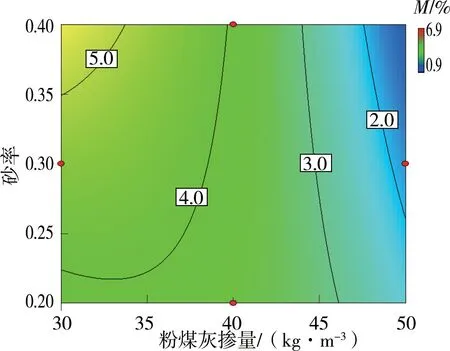
图3 砂率与粉煤灰掺量交互作用下质量损失率等值线（水胶比为1.0）

图4～图6为双因素交互作用下冻融后相对动弹性模量等值线图（以相对动弹性模量最大时的双因素交互作用图进行说明）。分析单因素影响作用可知，相对动弹性模量随着水胶比和砂率的增大而减小，随着粉煤灰掺量的增大而增大，且在设计试验组范围内，水胶比为1.0、砂率为0.2、粉煤灰掺量为50 kg／m3时胶凝砂砾石冻融后相对动弹性模量最大。分析双因素交互作用可知，水胶比与砂率交互作用下相对动弹性模量变化范围为26%～34%，水胶比与粉煤灰掺量交互作用下相对动弹性模量变化范围为32%～35%，砂率与粉煤灰掺量交互作用下相对动弹性模量变化范围为28%～34%。说明，水胶比与砂率的交互作用对胶凝砂砾石冻融后相对动弹性模量的影响最为显著。原因是动弹性模量与所测材料的密实度有关，当砂率增大时，细砂形成的孔洞增多，增多的孔洞为胶凝材料提供了更大的水化空间，但同时降低胶凝砂砾石的密实度，故随砂率增大质量损失率和相对动弹性模量减小。

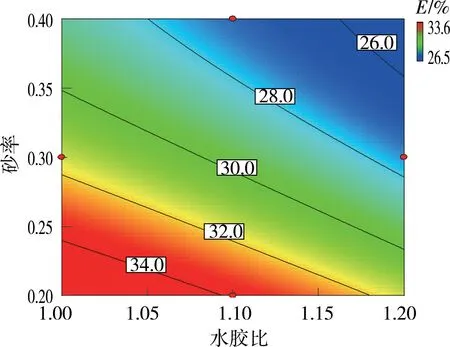
图4 水胶比与砂率交互作用下相对动弹性模量等值线（粉煤灰掺量为50 kg／m3）

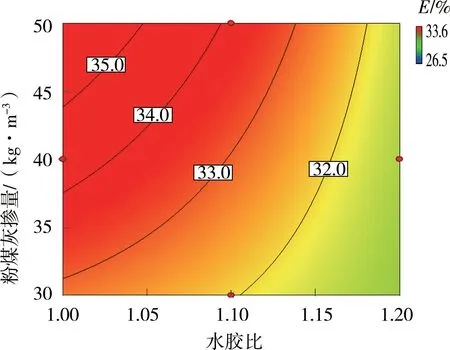
图5 水胶比与粉煤灰掺量交互作用下相对动弹性模量等值线（砂率为0.2）

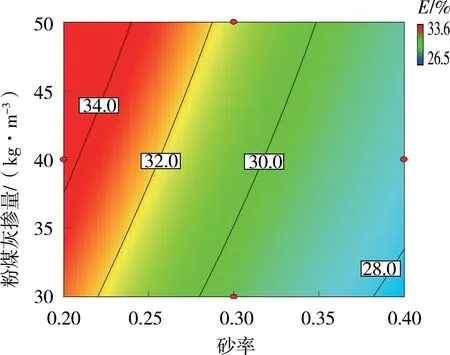
图6 砂率与粉煤灰掺量交互作用下相对动弹性模量等值线（水胶比为1.0）

3 响应面多目标优化

基于已建立的拟合模型，结合响应面的渴求函数对胶凝砂砾石材料配合比进行多目标优化，寻求最优的水胶比、砂率及粉煤灰掺量，从而实现质量损失率最小化、相对动弹性模量最大化。某一响应的渴求值（di）定义在0～1范围内，当响应值落在期望水平时di取1，当响应值处于可接受范围之外时di取0。目标最小化和最大化的di计算式分别为

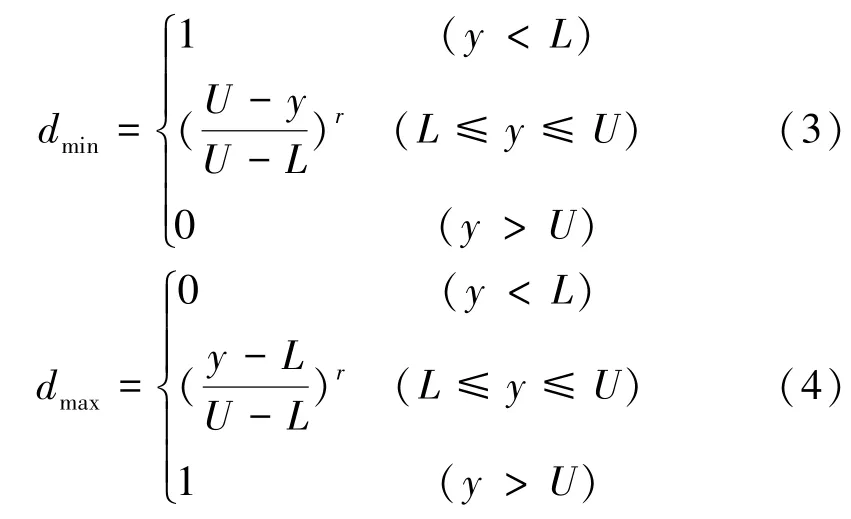
式中：r为调形系数；y、U与L分别为第i个响应的拟合值、上限值与下限值。

表7 胶凝砂砾石材料参数优化限制条件

胶凝砂砾石作为贫胶凝材料，其耐久性很大程度上取决于胶凝材料的用量［16］。针对不同粉煤灰掺量的胶凝砂砾石配合比进行优化，结果表明：最优砂率为0.2，最优水胶比与粉煤灰掺量相关，当粉煤灰掺量为30 kg／m3时最优水胶比为1.06，当粉煤灰掺量为40 kg／m3时最优水胶比为1.04，当粉煤灰掺量为50 kg／m3时最优水胶比为1.01。

4 结 论

（1）响应面可以建立较为精确的以水胶比、砂率和粉煤灰掺量为因素的胶凝砂砾石冻融后质量损失率、相对动弹性模量回归模型，基于该模型利用渴求函数可以实现抗冻性能的多目标优化。

（2）影响胶凝砂砾石冻融后质量损失率的单因素显著顺序为粉煤灰掺量、砂率、水胶比，双因素为水胶比、粉煤灰掺量；影响相对动弹性模量的单因素显著顺序为砂率、水胶比、粉煤灰掺量，双因素为水胶比、砂率。

（3）通过配合比多目标优化设计，得到胶凝砂砾石材料的最优砂率为0.2，粉煤灰掺量为30、40、50 kg／m3时对应的最优水胶比分别为1.06、1.04、1.01。