基于蚁群算法优化极限学习机模型的滑坡位移预测

曹 博， 汪 帅， 宋丹青， 杜 涵， 刘光伟， 周志伟

(1.辽宁工程技术大学 矿业学院， 辽宁 阜新 123000； 2.清华大学 水沙科学与水利水电工程国家重点试验室，北京 100084； 3.神华宝日希勒能源有限公司露天煤矿， 内蒙古 呼伦贝尔 021000)

1 研究背景

我国是世界上滑坡灾害发育最为严重的国家之一[1-2]，它的频繁发生和快速运动，每年都会造成大量的人员伤亡和财产损失[3]。2018年的《全国地质灾害通报》表明，2017年全年我国共发生地质灾害2 966起，其中滑坡灾害1 631起，占比为55.0%，因此，如何有效防止滑坡灾害成为了该研究领域的热点问题。

近年来，滑坡位移预测已逐渐成为滑坡早期预警的有效手段，它允许研究人员通过室内计算来分析滑坡历史变形的主要特征，并对未来一段时间内滑坡的位移趋势进行预测[4]。由于该方法所需成本较低并且精度较高，因此得到了快速发展。目前常用的滑坡位移定量预测方法主要包括数理统计模型和非线性理论[5]，2009年Li等[6]提出在滑坡预测过程中使用尖点突变模型，王珣等[7]在2017年建立切线角模型进行了临滑预报判据研究，但是这些方法通常需要对滑坡的演化状态进行较为深入准确的分析，不确定性较大。与这些模型相比，机器学习模型不需要分析复杂的滑坡机理且对于以滑坡为代表的非线性动态系统具有较好的拟合效果，因此应用更加广泛，最具代表性的模型包括2019年柳青等[8]进行滑坡位移预测预报所采用的神经网络模型、Zhou等[9]和李仕波等[10]先后于2016及2019年预测位移时采用的支持向量机模型、2015年周超等[11]预测滑坡位移时引入的混沌理论。极限学习机模型(extreme learning machine, ELM)作为近年来应用广泛的智能算法，其在滑坡位移预测方面的适用性得到了不少研究的验证，如Cao等[12]利用ELM模型对白家包滑坡的位移进行了预测，同时与支持向量机模型进行了预测效果比较；Huang等[13]对滑坡位移利用混沌理论和小波变换进行分解后，再基于ELM模型进行了非平稳时间序列的预测。在ELM模型的计算过程中，由于有个别参数是随机选取的初始值，因此为加快收敛速度并提高准确性，需要加入一定的算法进行选参优化，如粒子群算法[10]、遗传算法[5]、蚁群算法[14]等常见方法。然而，对于多个算法优化效果的对比，前人的研究较为欠缺。

综上所述，为验证ELM模型在我国三峡库区滑坡位移预测中的适用性，本文选择湖北秭归八字门滑坡为研究对象，在深入分析其变形历史和影响因素后，完成了基于蚁群算法优化ELM模型的位移预测过程，并通过对比验证了不同优化算法的优化效果，以期为后续研究提供科学依据。

2 蚁群算法优化极限学习机模型

2.1 基于移动平均法的时间序列分解

基于时间序列分析原理，对于通过监测或遥感等手段得到的滑坡位移数据，可以将其看成是一种非线性时间序列，并且有如下关系[15]：

yt=St+Ct+εt

(1)

式中：yt为滑坡累计位移，mm；St、Ct和εt分别为滑体的趋势项、周期项和随机项位移，mm。其中，趋势项位移代表了滑体在长时间段内的变形趋势，通常为单调递增；周期项位移表示滑坡位移在周期性因素影响下的变形；随机项位移为滑坡在随机因素影响下产生的位移，由于影响因素较难量化，因此以往研究通常将该项忽略。

对于滑坡位移预测的研究，通常要利用一定的方法将滑坡的累计位移分解成不同的分量，通过对子序列进行分析预测，叠加所有子序列的预测值来得到总的滑坡位移预测值。分解方法主要包括两种，即数理统计法和智能方法，后者又包括小波分解[11]、经验模态分解[16]、集合经验模态分解[17]等方法，但是这类方法总体来说较为复杂。针对滑坡位移时序的特点，本文选择移动平均法进行总位移的分解，其计算公式如下：

Mi={M1,M2,…,Mt,…,Mn}

(2)

(3)

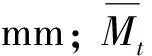
2.2 极限学习机

2006年Huang等[18]首先提出了极限学习机，其本质是一种单层神经网络，但相比较而言，ELM模型的结构更为简单，且运算速度更快[19]，并且其中的层间连接权值及隐含层偏差不需要事先设置。在ELM算法中，隐含层神经元阈值及输入层与隐含层的连接权值由函数生成，训练过程中无需人为干预，只需进行隐含层神经元个数设置即可获得该条件下的最优解。

若设模型中输入层与隐含层之间连接权值为w，同时隐含层与输出层间的连接权值为β，给定训练样本总数为Q，ELM神经网络的输出为T，激活函数为g(x)时，隐含层输出矩阵H可由下式求解：

Hβ=T′

(4)

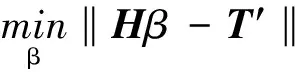
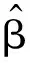
(5)

式中：H+为输出矩阵H的广义逆矩阵。

极限学习机模型在理论上可以获得最小的训练误差，利用ELM模型进行滑坡位移预测模型构建的过程中，所需考虑的参数仅为隐含层神经元个数，利用ELM模型进行位移预测主要包含以下步骤：

(1)对隐含层相关参数随机进行初始化，确定隐含层神经元个数，并随机生成输入层与隐含层间的连接权值及隐含层神经元偏差的初始值；

(2)合理选择一个无限可微函数作为隐含层激活函数，以便求解隐含层输出矩阵H；

2.3 蚁群算法优化极限学习机

Parpinelli等[20]于2002年首次提出了蚁群算法，蚁群算法类似于自然界中蚂蚁的觅食过程，蚂蚁群体会通过不同路径搜寻食物，对于正确的路径，蚂蚁的数量和密度会越来越大，而对于其他路径则相反。最后蚂蚁能够搜寻到一条抵达食物源头的最佳路径，即问题的最优解[20-21]。蚁群算法最初用于旅行商难题上，随着科研人员的不断探索，应用范畴几乎涉及各个领域。为更好更快地找到最优的连接权值与神经元阈值，本文拟采用蚁群优化算法对极限学习机模型进行改进，以达到更优的计算效果。

使用蚁群算法优化极限学习机模型的流程如下所示：

(1)初始化参数，计算蚂蚁从一个点转移到另一个点的概率，概率计算公式如下：

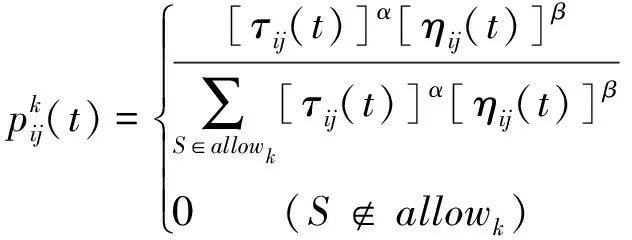
(6)

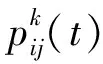
(2)通过不停迭代，寻求一个最佳的觅食路径，确定蚁群算法全局最优路径，即极限学习机的权值和阈值；

(3)基于蚁群算法最优路径的计算，合理选择隐含层激活函数，求解隐含层输出矩阵H；

(4)对输出层权值矩阵进行求解，以此为基础进行滑坡位移预测。

3 研究实例

3.1 八字门滑坡概况

八字门滑坡位于湖北省宜昌市秭归县归州镇香溪河右岸，距离三峡大坝38 km。滑坡高程分布在140～270 m之间，滑体平均长度和平均宽度分别为350和400 m，厚度约为30 m，体积达400×104m3，属于大型堆积层滑坡。根据野外钻孔揭露的情况显示，滑坡包括两层滑带，上部为次级滑面，厚度约为3 m，下部的主滑带连续分布，中部的厚度最大。滑坡基岩为侏罗系香溪组(J1x)的砂岩和泥质粉砂岩，呈强分化特性，局部夹杂有炭质泥岩。八字门滑坡平面及剖面图如图1所示。

3.2 滑坡变形特征及影响因素分析

自从八字门滑坡发生较为明显的变形开始，地质灾害管理部门就对其变形进行了持续的监测，主要包括深部位移和地表GPS位移。在滑坡的监测剖面Ⅰ-Ⅰ′上(图1)，安装了3个地表监测点(ZG110、ZG111、ZG112)和1个深部位移监测点(QTZK3)，监测点多年监测结果以及相应的库水位和月降雨量变化见图2，2005年3月与2004年9月相比滑坡深部监测点的相对位移如3所示。

3个地表监测点的高程分别约为165、191和215 m，可以代表滑坡前、中、后部的变形特点和趋势。图2中滑坡累计位移曲线显示，更靠近滑坡后缘的ZG111监测点的位移量最大，总位移超过了1 700 mm，因为该点所在位置是滑坡的陡坎处，在每年的雨季和库水位下降期(5-9月)，该点都会发生较为明显的阶跃式变形增长，如从2009年的5月开始，在5个月的时间内，该点的累计位移增长超过了200 mm，增长率达到了24.9%。但是位于滑坡中部的ZG110监测点和靠近滑坡前缘的ZG112监测点的总位移却较小，分别约为1 200 mm和360 mm，且该两个监测点的位移增长趋势较为平稳。上述结果说明八字门滑坡的运动模式为“前进式”，即最开始由滑坡上部发生蠕变并向下挤压，随着位移的逐渐增加，变形开始向滑坡前缘发展，最终形成整体破坏。

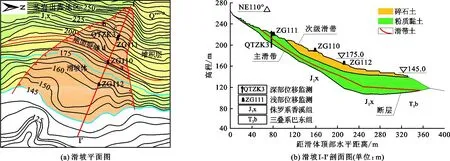
图1 香溪河八字门滑坡平面及剖面图

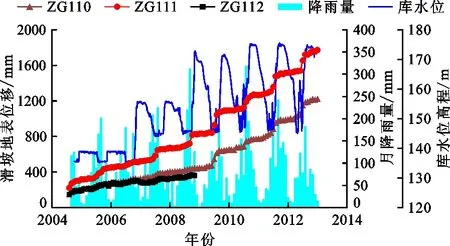
图2 2004-2012年八字门滑坡各监测点地表位移监测曲线以及相应库水位和月降雨量变化

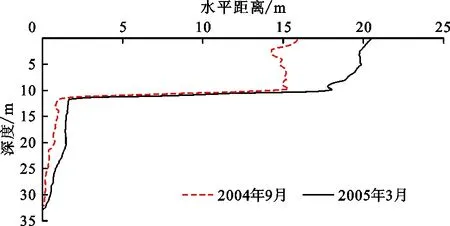
图3 八字门滑坡2005年3月相对于2004年9月深部监测点的位移

选取变形量最大的ZG111监测点对滑坡影响因素和变形间的响应关系进行分析，在三峡水库蓄水前，滑坡前缘被库水淹没，加之地下水上升带来的侵蚀作用，滑动面前部的抗剪强度逐渐降低，引起了滑坡前部的缓慢蠕变，并在前缘逐渐形成了少量张拉裂缝，因此在这段时间内滑坡存在渐进式变形的特征。2003年三峡水库开始蓄水，在八字门滑坡上出现了较多的变形迹象；同年8月，滑坡体上道路两侧出现了两个较大的裂缝，长度分别达到了30和45 m；2004年的5月至8月，库水位短暂下降，在道路上又发现了多处裂缝，如图4所示。

图4 八字门滑坡体上公路变形实拍图

由于水库的周期蓄水，滑坡的累计位移也随之发生变化。在2007年2-4月，水库水位由156 m下降至152 m，但累计位移几乎不变，但是在该年的5-9月，由于总降水量达到近600 mm，该点的累计位移迅速增加，变化量超过了120 mm，同时伴随有多处地表裂缝的出现。这是因为短时间内的强降水导致地下水位的抬升，而该滑坡主要由堆积物构成，高孔隙率和良好的渗透性使得地表水的入渗更加容易，导致了异常的孔隙水压力和水动力压力诱发的滑坡变形。综上所述，滑坡的变形主要受到了库水位波动和降雨入渗的影响。

3.3 滑坡位移分解及预测

3.3.1 基于移动平均法的累计位移分解 由于ZG111测点处的累计位移最大，而且可以反映滑坡的阶跃式变形特点，因此选取该点进行位移预测。总计获取102组数据，将前90组数据作为训练数据集，后12组数据作为测试数据集，首先根据公式(1)、(2)将2005年7月至2013年1月的全部数据分为趋势项位移和周期项位移，如图5所示。由图5可看出，提取出的趋势项位移较为平滑，基本不存在突变现象，说明移动平均法可以很好地消除滑坡阶跃式曲线的影响，从而反映出真正的滑坡长期变形特征。另一方面，滑坡的周期项位移也具有较明显的周期特征，而且初步估计该曲线的周期近似为12个月，也符合实际情况。

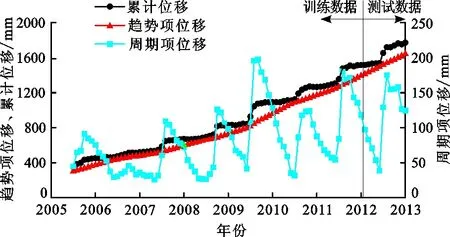
图5 2005年7月至2013年1月八字门滑坡ZG111测点累计位移分解结果

3.3.2 滑坡位移分量预测 趋势项位移反映滑坡长时间以来的变形趋势，在目前的研究中该位移多使用多项式函数进行预测。对于上节中分解得到的趋势项数据，利用最小二乘法进行预测。选取图5中前79组数据先进行拟合，采用二次多项式作为拟合函数，拟合之后再将公式外推获得后面测试数据集的预测结果，利用本案例的训练数据最后获得的预测公式如下：

y=0.0955t2+6.0632t+324.59 (R2=0.998)

(6)

趋势项位移预测结果公式(6)的拟合优度达到了0.998，表明该公式的预测效果很好，能够有效反映滑坡变形随时间变化的整体趋势。

对于周期项位移数据，它通常与滑坡的周期性影响因素有关，本文选取降雨和库水位变化作为滑坡周期性的影响因素，再参考类似研究，还需要考虑滑坡变形对两种诱发因素的响应滞后时间。因此，最终选择上月降雨量、当月降雨量、上月库水位平均高程和当月库水位平均高程作为影响因素。这些影响因素被作为输入数据集，而当月周期项位移被作为输出数据集，然后基于自编代码构建蚁群算法优化的极限学习机模型，进行周期项位移的预测。以2012年2月至2013年1月为预测期，得出的滑坡趋势项位移和周期项位移预测结果与实际值比较如图6所示。由图6可看出，周期项位移预测结果与实际较为吻合，表明预测效果也较为理想。

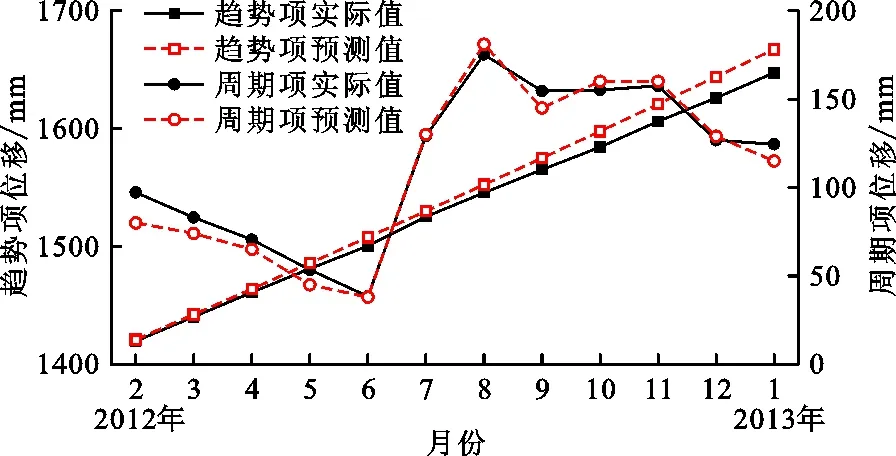
图6 2012年2月至2013年1月滑坡趋势项和周期项位移预测结果与实际值比较

4 讨 论

将3.3节得到的趋势项和周期项两项分量相加，得到预测期蚁群算法优化的极限学习机模型预测的最终累计位移结果，如图7所示，同时，将单一的极限学习机模型预测结果以及采用两种常用的优化算法(粒子群算法和遗传算法)对极限学习机模型进行优化后的预测结果一并绘入图7，并与位移实际值进行比较，以分析本文所采用的蚁群算法优化的极限学习机模型的预测效果。上述各模型预测效果主要参数对比见表1。

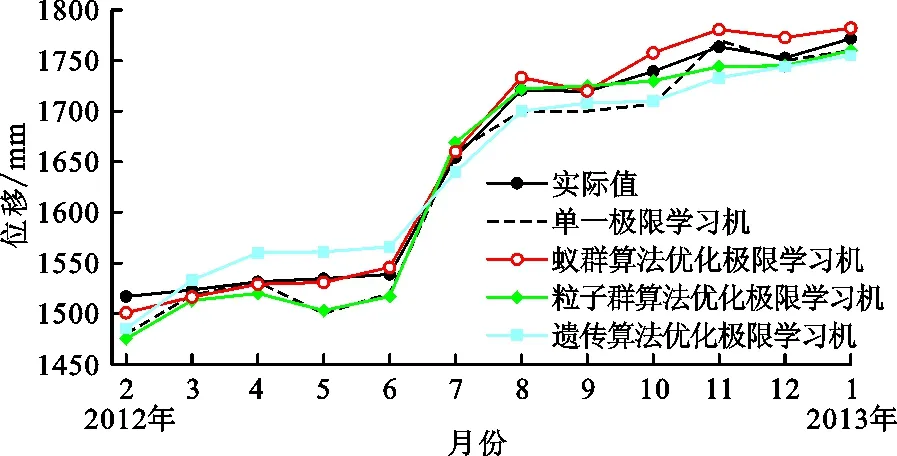
图7 各模型预测结果

分析图7和表1可知：(1)在所有4种模型当中，单一极限学习机模型的计算用时最短，但是其计算精度最差，平均误差达到了23.5 mm，拟合优度为0.973，此2项指标均低于其他3种预测模型。然而，考虑到滑坡的累计位移已经超过了1 000 mm，因此单一极限学习机模型的预测精度也是可以接受的，这说明该模型在阶跃式滑坡位移曲线方面的预测是较为可靠的，也验证了极限学习机模型对于本文应用实例的适用性。(2)对于优化后的极限学习机模型，蚁群算法优化的极限学习机计算用时为98 s，位移预测结果平均误差为10.1 mm，预测结果拟合优度为0.998，各指标均优于其他两种算法优化的极限学习机模型。因此，对于本文所示的案例而言，蚁群算法具有最佳的参数选取与优化效果，蚁群算法优化的极限学习机模型是进行三峡库区八字门滑坡累计位移预测的最优模型，可在类似滑坡体的位移预测中进一步研究与推广。

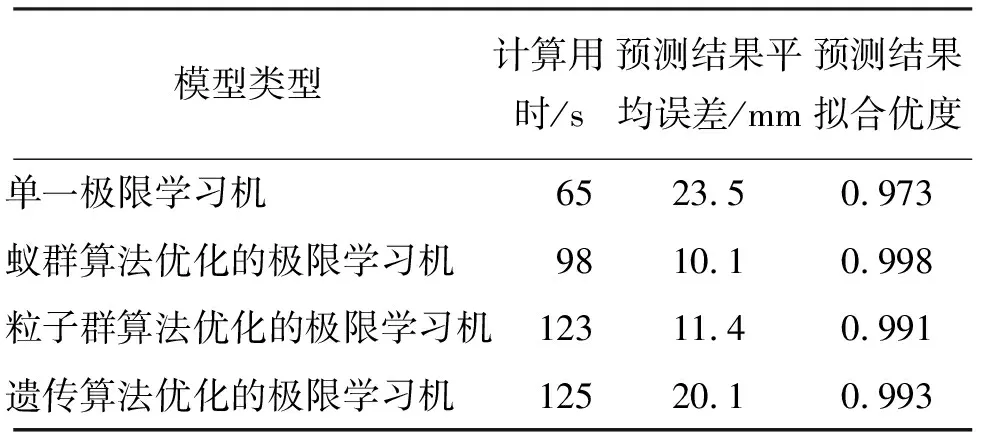
表1 各模型预测效果主要指标对比

5 结论与展望

本文探讨了蚁群算法优化的极限学习机模型在三峡库区堆积层滑坡位移预测中的应用，并以秭归县八字门滑坡为例进行了预测效果分析，主要得到以下几点结论：

(1)极限学习机模型能够较好地进行三峡库区八字门滑坡的累计位移预测，单一极限学习机模型预测的平均误差为23.5 mm，拟合优度可达0.973，是一种可靠的位移预测方法。

(2)蚁群算法优化的极限学习机模型比单一的极限学习机模型的预测精度更高，说明该算法的优化性能较好；同时与其他2种传统的优化算法(粒子群算法、遗传算法)相比，蚁群算法在计算用时和计算精度上更优，其预测结果与实际结果间的平均误差为10.1 mm，拟合优度达0.998。该模型可在类似滑坡的位移预测研究中进行推广。

(3)在蚁群算法优化参数选取的过程中，部分算法参数仍需进行进一步讨论，算法参数值与计算结果的用时和精度间的敏感性分析将会是未来的一个研究方向。