不同扩散角下单侧渐扩消力池水力特性研究
杜振康, 尹进步, 朱光明, 何 红, 闫秀秀
(西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)
1 研究背景
水利工程中常见的高坝泄洪消能问题往往是工程设计中十分关键而又复杂的技术问题[1-3],如果处理不当极易发生空蚀空化、冲刷破坏和结构失稳等问题[4]。消力池是水利工程中广泛使用的消能设施,选择合适的消力池体型,可大大提高消能率,从而降低高速水流带来的危害。常用的消力池按照消力池的宽度是否变化分为等宽矩形消力池、渐扩消力池和突扩消力池。对于等宽矩形消力池,国内外学者经过多年的研究,已取得丰富的成果,计算方法较为成熟[5-7]。在渐扩消力池和突扩消力池的研究方面,Hassanpour等[8]、张志昌等[9],Ferreri等[10]、傅铭焕等[11]、罗永钦[12]通过物理模型试验、数值模拟等方法,从不同角度进行了理论分析,并取得了一定的成果。
然而在有些工程中,由于受到特殊地形、地质条件的限制无法修建常规消力池,或常规消力池内参与消能的水体较少,不能满足消能要求,因而将消力池修建为单侧渐扩式,以增加消能水体,提高消能率。而对于模型试验方法现有的测试手段容易破坏原有的流场结构,难以详细了解消力池内部的漩涡结构和强度,因此有必要借助数值模拟方法得到连续、详细的流场信息。
Zhang等[13]、Chen等[14]采用三维数值模拟, 研究了多股多层水平淹没射流的流动特性、漩涡结构和消能机理。汪文萍等[15]基于数值模拟研究发现,单侧渐扩消力池在低坝工程应用中,当表、底孔联合泄水时能够优化消力池内流态、提高消能率。赵东阳等[16]通过数值模拟方法得出单侧渐扩消力池的压强、紊动能等水力要素分布特点,但研究对象只是针对某个具体角度的渐扩消力池,研究内容也主要集中在水面线、压强、消能率等方面。此外,国内外采用单侧渐扩消力池的工程较少,对其的研究缺乏一定的系统性,并且关于消力池扩散侧可能存在的漩涡问题鲜有涉及,因此有必要对单侧渐扩消力池的水力特性进行较为系统的研究。
本文基于国内某水利工程溢洪道的单侧渐扩消力池体型,在物理模型试验的基础上进行了三维数值模拟,通过改变消力池单侧扩散角,探究单侧渐扩消力池的流速特性、漩涡结构等水力要素的变化规律,相关研究成果可为进一步研究单侧渐扩消力池的水力特性及体型优化提供参考。
2 模型的建立与研究方法
2.1 实例工程溢洪道布置及模型建立
某水利工程溢洪道体型如图1所示。该溢洪道设置两孔开敞式有闸控制泄洪孔口,两闸门孔口尺寸均为6 m×6 m,堰型为WES(Waterways Experiment Station)实用堰,堰顶高程为915.5 m;泄槽宽度为14.0 m,在陡坡段设有两道掺气坎;泄槽出口为底流消能形式的单侧渐扩消力池,消力池单侧扩散角度为4.77°(工程设计体型)。消力池底板高程为834.0 m,进口与泄槽等宽,出口宽度为20.38 m,消力池长度为84.53 m,在消力池出口直立尾坎顶部设置高2.5 m、宽1.5 m的不连续梯形墩。溢洪道桩号设定以溢流堰前端为0+0.00 m,消力池尾桩号为0+272.00 m。
数值计算设定如下:定义溢流堰前端为X=0,右侧边墙外为Y=0,消力池底板以下5.9 m处所在水平面为Z=0。计算区域包括进水渠、控制段、泄槽、消力池及部分海漫;模型上、下游为压力边界,上游水位高程为923.05 m,下游水位高程为846.81 m(校核洪水泄洪工况),顶部为压力边界;左右两侧及底部壁面均采用无滑移边界条件。建立的溢洪道计算模型如图2所示。
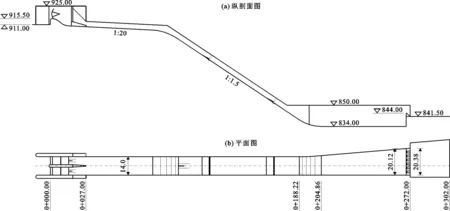
图1 实例工程溢洪道体型(单位:m)
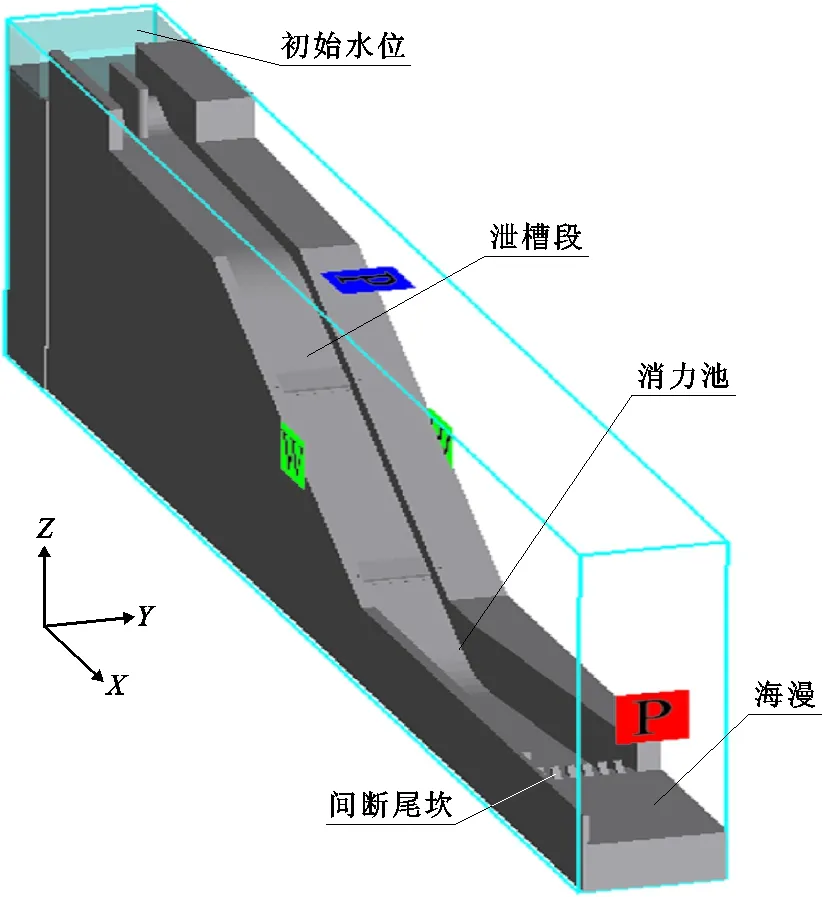
图2 溢洪道计算三维模型
2.2 三维数值模型网格单元尺寸
对模型采用结构化正交网格进行划分,为验证网格尺寸对计算结果精度的影响,分别采用0.3、0.5、0.8和1.0 m 4种网格单元尺寸进行计算,并将该4种网格单元尺寸计算得到的消力池末端流速与试验测试结果进行对比,得出相对误差,相对误差随网格单元尺寸的变化曲线如图3所示。由图3可见,随着网格单元尺寸的减小,相对误差不断减小,当网格单元尺寸为0.3和0.5 m时,其相对误差小于4%,可认为计算结果的精度满足要求。因此,为提高计算效率同时又保证计算精度,最终采用网格单元尺寸为0.5 m。
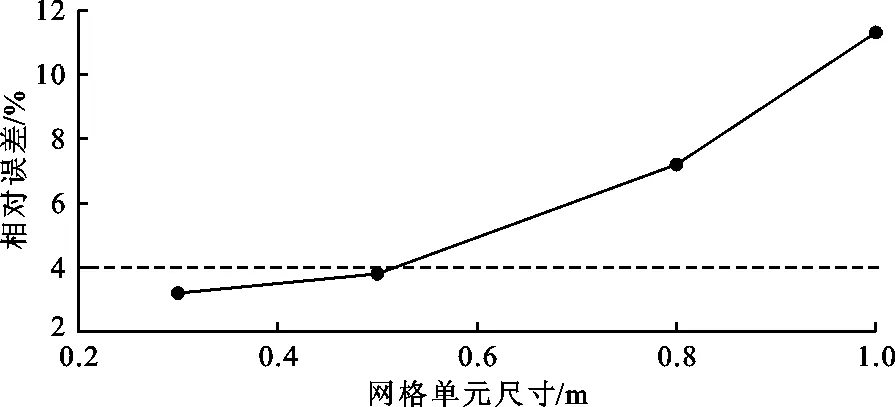
图3 数值模型网格单元尺寸与计算结果相对误差关系曲线
2.3 三维数值模型的控制方程
对于RNG(renormalization group)k-ε双方程紊流模型通过修正湍动黏度,考虑平均流动中的旋转及旋流流动情况,能够更好地处理高应变率、流线弯曲程度较大的流动[17]。故采用RNGk-ε双方程紊流模型对单侧渐扩消力池进行数值模拟,各控制方程见方程式(1)~(5)。
连续方程:
(1)
动量方程:
(2)
紊动能k方程:
Gk-ρε
(3)
耗散率ε方程:
(4)
(5)
(6)
式中:ρ为密度,kg/m3;t为时间,s;xi、xj为坐标分量;p为压强,Pa;ui、uj分别表示i、j方向的时均流速,m/s;μ为动力黏性系数,N·s/m2;μt为紊流黏性系数,N·s/m2,其数值可由紊动能k和紊动能耗散率ε求得;Gk为湍动能产生项;Cε1=1.42,Cε2=1.68,η0=4.377,β=0.012;σk、σε分别为k和ε所对应的紊流普朗特数。
采用TruVOF(true volume of fluid)方法追踪水流自由表面,定义流体体积函数F的运输方程为:
(7)
式中:Ax、Ay、Az分别为x、y、z3个方向可流动的面积分数;u、v、w分别为x、y、z3个方向的流速,m/s;VF为可流动的体积分数。F=0表示单位体中流体体积分数为0,即空单元;F=1表示单位体完全被流体充满;F=0~1表示单位体中被流体局部充满。
2.4 计算方案
以实例工程采用的消力池单侧扩散角度θ=4.77°作为工程方案(记作方案S2),该方案校核工况上游水位为923.05 m,下游水位为846.81 m,泄流量为513.30 m3/s,利用方案S2的模型试验数据来验证数值模拟的准确性。另外为探究不同角度单侧扩散消力池的水力特性,在其他水力参数不变的情况下,引入θ=3°、6°、9°、12° 4个扩散角,分别对应S1、S3、S4、S54个方案,各方案单侧扩散消力池体型如图4所示。
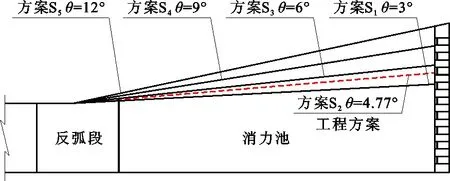
图4 各方案单侧扩散消力池体型示意图
3 结果与分析
3.1 数值模型验证
通过试验测得工程方案下消力池内中轴线上底板时均压力和水面线的值,与数值模拟的计算结果进行比较,来验证数值模型模拟结果的准确性。图5、6分别为消力池段水面线和消力池底板时均压力的模拟计算值与试验值对比。
由图5可以看出,消力池水面线的计算值与试验值基本吻合,消力池首部偏差相对较大,最大偏差为7.2%(桩号0+210.00 m);由图6可以看出,消力池底板时均压力的计算值与试验值沿程分布规律基本一致,位于池首的几个测点偏差较大,但之后各测点的计算误差均小于10.0%。其原因可能是消力池首部水流流速较大,水流掺气剧烈且水面破碎,而消力池后半段流态相对稳定,水面较为平稳,因此,池首水面线和时均压力的计算值与试验值相比均存在相对较大的误差,在消力池中后部,模拟计算结果与试验结果基本一致。
总体来看,通过模拟计算得到的消力池水面线和底板时均压力分布基本满足水流规律性研究的精度要求,因此可基于所建立的三维数值模型进一步研究单侧渐扩消力池的水力特性。
3.2 各方案消力池底板流速分布
各方案不同单侧扩散角度下消力池近底(Z=6.2 m)流速平面分布云图如图7所示。
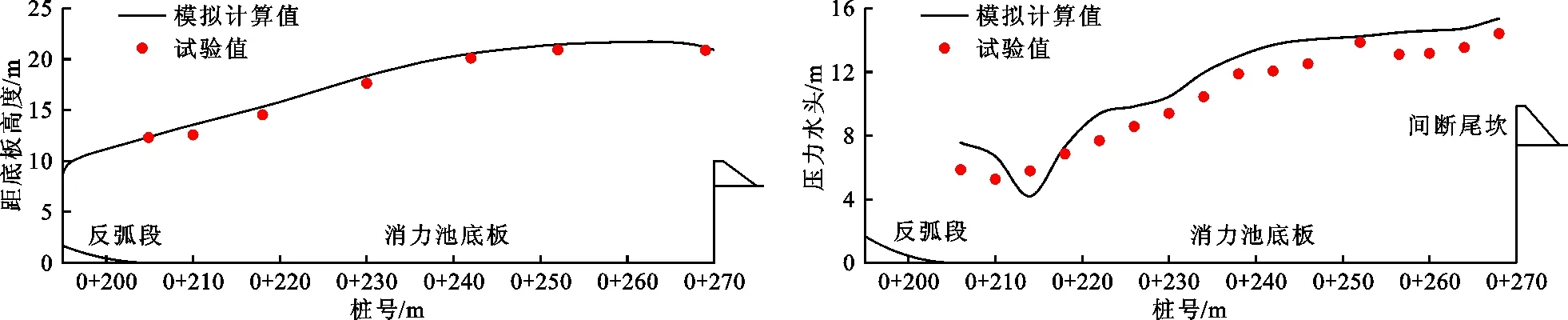
图5 消力池水面线的模拟计算值与试验值对比 图6 消力池底板时均压力模拟计算值与试验值对比
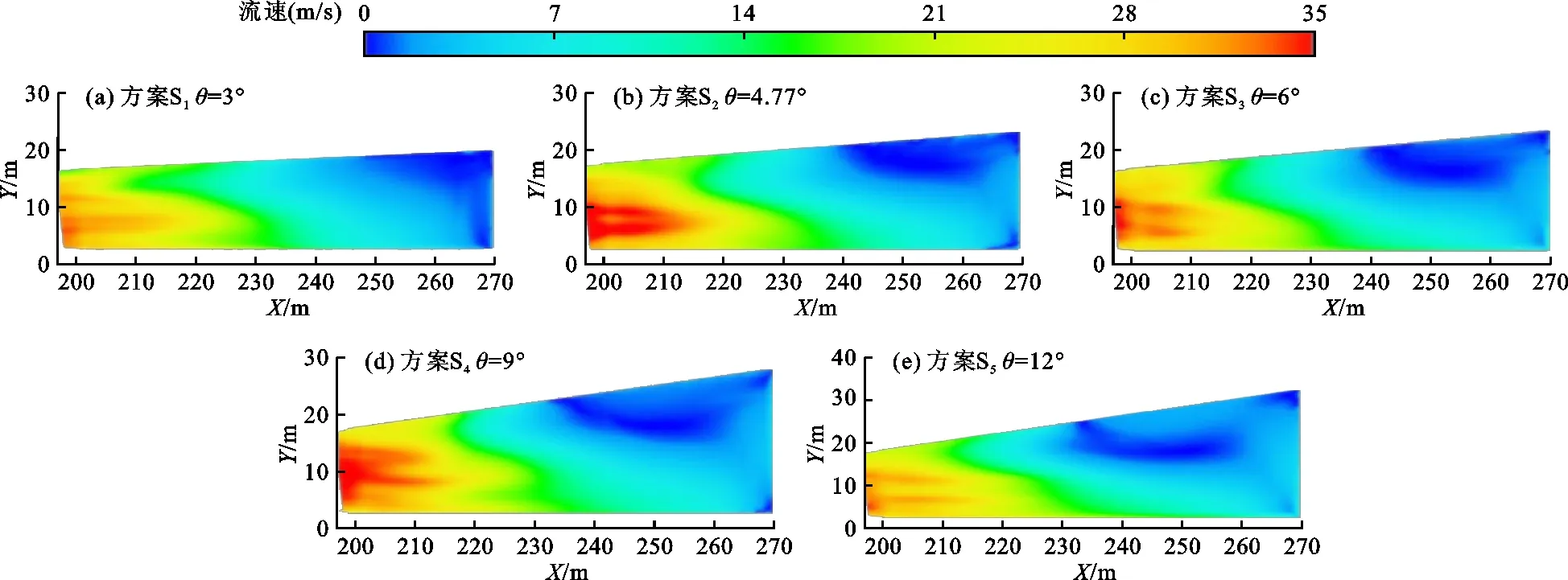
图7 各方案不同单侧扩散角度下消力池近底流速平面分布(Z=6.2 m)
由图7可知,消力池近底流速呈不对称分布,同一桩号断面靠近扩散侧的流速明显小于非扩散侧,高速水流区均出现在消力池池首,且靠近非扩散侧。随着单侧扩散角度的增大,消力池扩散侧尾部低流速区缓慢上移,由方案S1的桩号0+247.00 m缓慢上溯至方案S5的桩号0+231.00 m附近,即随扩散角度的增大,扩散侧流速逐渐降低。相反,随着扩散角度的增大,消力池非扩散侧尾部低流速区范围逐渐减小并且尾部流速也相应增大。究其原因,由于消力池边墙为单侧渐扩型式,高速水流经反弧段流入消力池,在消力池内形成不对称的三元水跃,池首为跃首处,流速大、紊动剧烈,之后消力池断面临底流速沿程逐渐减小,这种临底流速分布模式为降峰型[18],与传统底流消力池分布规律类似。由于消力池非扩散侧边墙的约束,水流只能沿纵向流动,使非扩散侧边墙流速明显大于扩散侧。随着单侧边墙扩散角度的增大,扩散侧参与消能的水体增加,流速逐渐降低。
表1给出了消力池单侧不同扩散角度对应的最大临底流速计算结果。临底流速是消力池安全稳定运行中的一个重要参数,最大临底流速的大小直接影响消力池底板的稳定性。有关突扩消力池的研究表明[19-20],最大临底流速随突扩比的增大而减小,且变化幅度较大。而对于单侧渐扩式消力池而言,由表1可以看出,随消力池单侧边墙扩散角的增大,临底流速最大值先增大后减小,当扩散角度θ=9°时达到最大值,此时临底流速为36.0 m/s,但不同方案下最大临底流速变化幅度较小,这与突扩消力池存在明显差异。此外,最大临底流速均发生在消力池首部,且随着扩散角度的增大,其位置逐渐向非扩散侧移动,这可能是因为扩散角的增大使入池水流纵向流速梯度增大,在非扩散侧边墙的束缚下,池内主流靠近非扩散侧。
3.3 消力池内的漩涡特性
消力池内流态复杂,水流掺混剧烈,且不对称布置易形成漩涡结构,漩涡对建筑物的影响一直以来都是学术界研究的重要课题。在单侧渐扩式消力池中,高速水流进入消力池后,主流带动周围水体产生强烈紊动。非扩散边墙侧的流速较大而流速梯度相对较小,且受边墙的束缚,不易形成漩涡。而扩散边墙侧的流速梯度较大,水流剪切作用强,易形成立轴漩涡。漩涡是能量耗散的重要途径,但贯穿性立轴漩涡极易形成水气两相流,在消力池底板引起强烈的压力脉动,对消力池底板的稳定安全造成威胁。
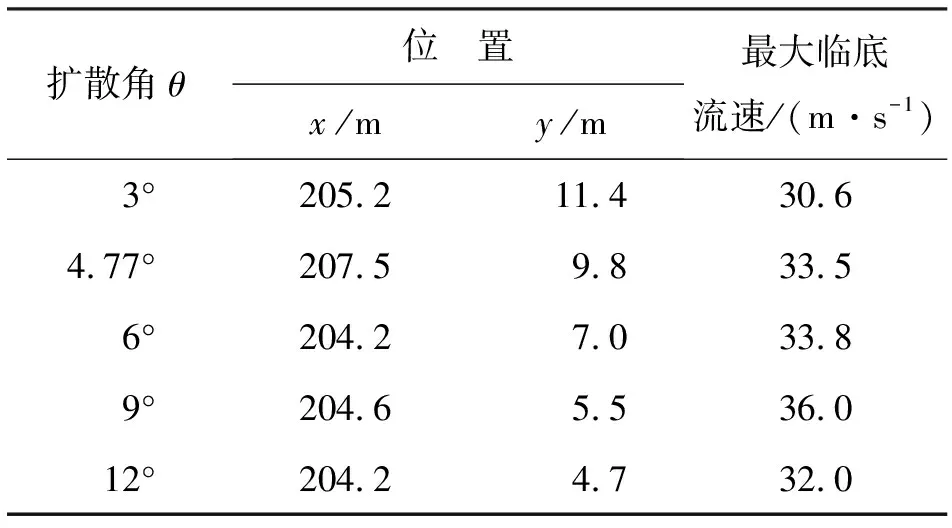
表1 消力池单侧不同扩散角度对应的最大临底流速
在物理模型试验中,由于消力池内水流流态复杂,难以观测漩涡的水力特性,因此利用数值模拟的方法对消力池立轴漩涡展开研究。因方案S3、S4的平面流场特性分别与方案S2、S5类似,故选择方案S1、S2、S53个具有代表性的方案,分别截取4个不同高度(Z=6.20、9.42、12.63、16.93 m)的水平剖面,模拟计算其流场分布,各代表性方案不同高度的平面流场分布及漩涡示意图如图8所示。
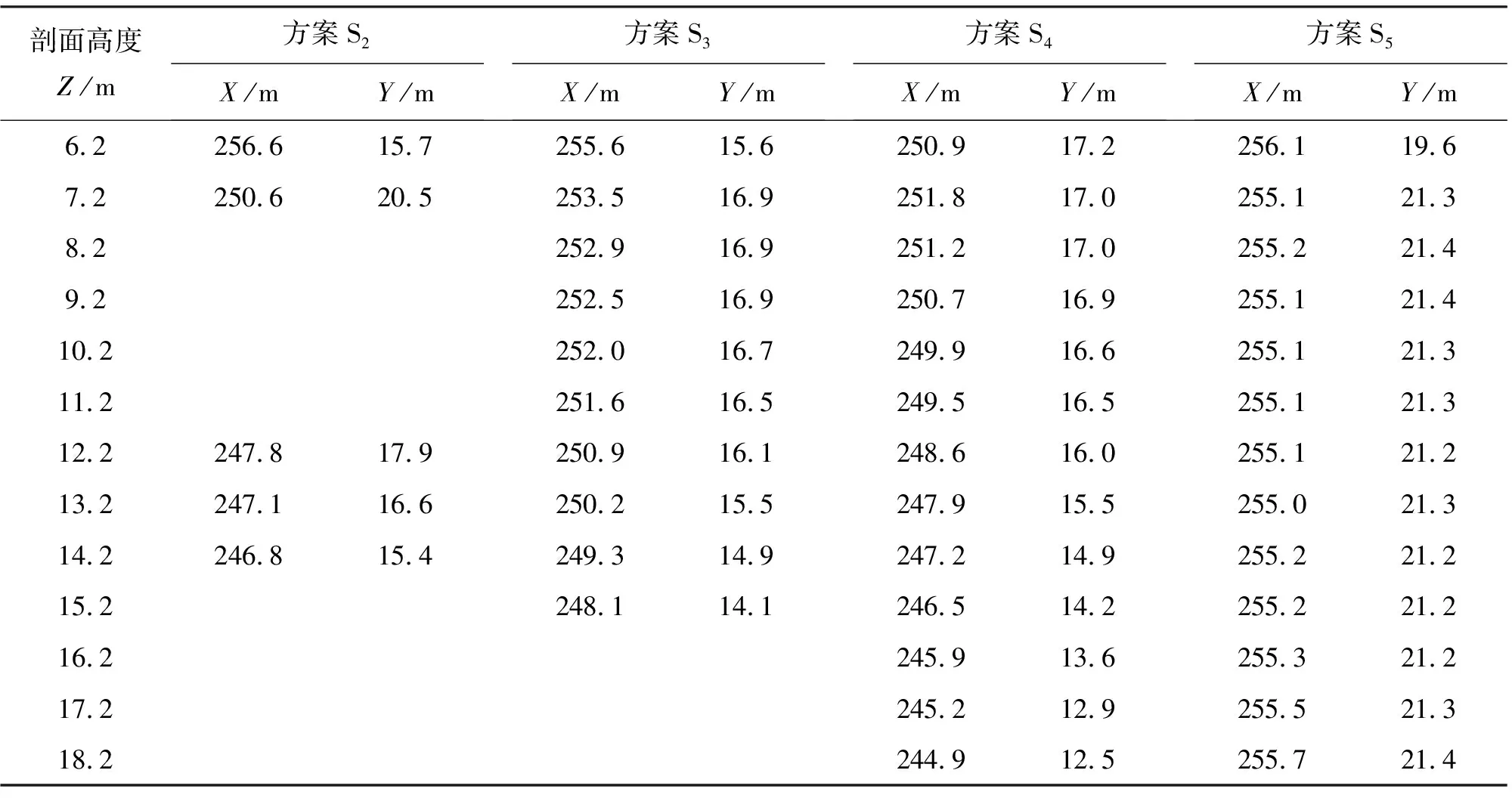
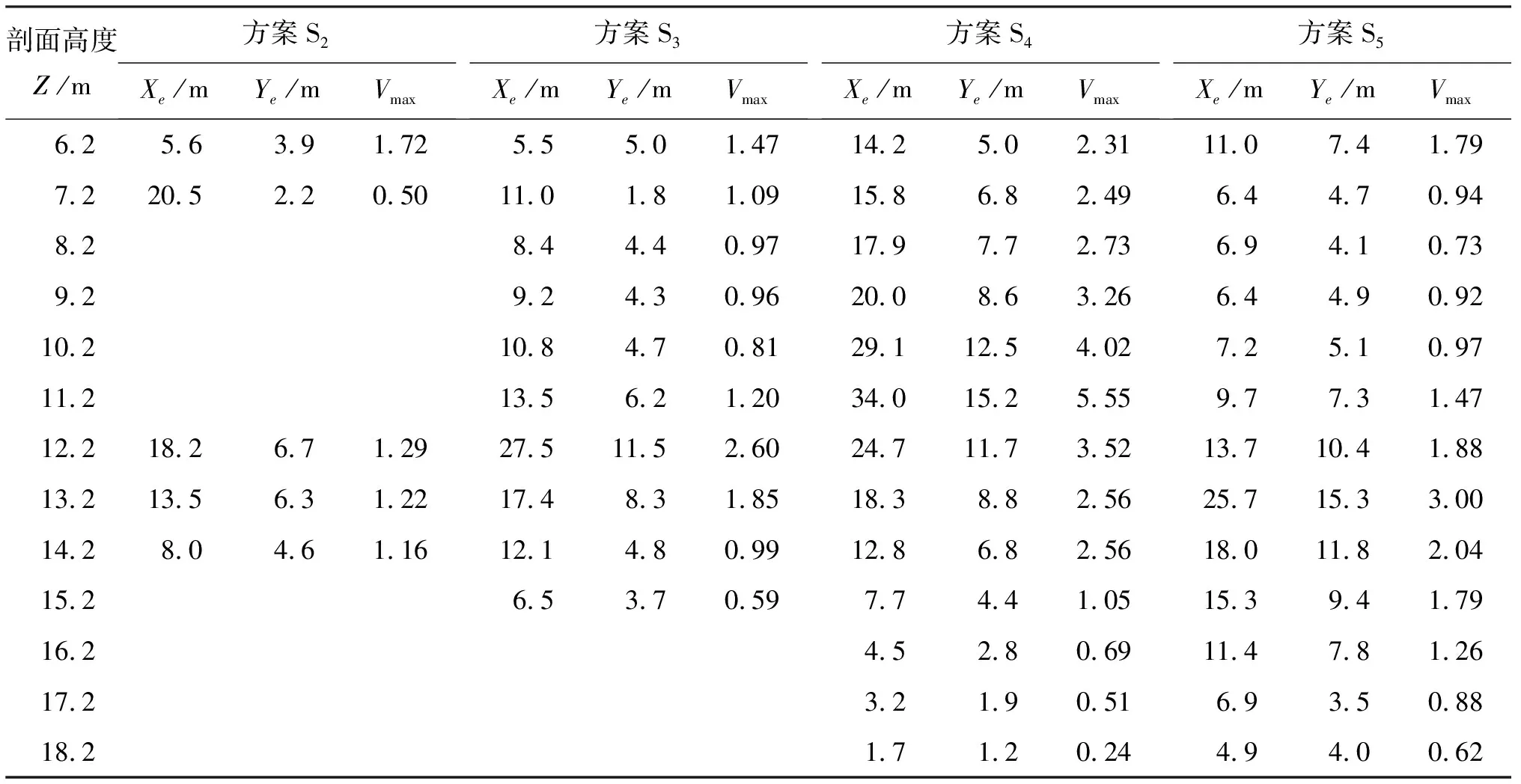
为了深入研究分析消力池内漩涡随单侧扩散角度的发展状况及其特性,选取方案S2~S5提取各方案不同高度水平剖面漩涡的涡心位置和强度指标,分别见表2、3。
结合图8与表2对各方案消力池内的漩涡流态特征分析如下:(1)方案S1仅在消力池底板附近出现小尺度漩涡,在复杂的消力池流态影响下,漩涡间歇性出现,涡心处流速为0.28 m/s,时均压强为149 kPa。随着水平高度的增加,消力池内无漩涡产生,池首逐渐出现回流区,且回流区范围随着水平高度的增加而向下游延伸,这是由于消力池内形成了稳定的淹没水跃,在平面流场中出现了回流现象。由此可见,当扩散角度较小时,单侧扩散消力池内的流态与传统矩形消力池类似。(2)在方案S2下,消力池8.2 m 由表3可知,各方案消力池内漩涡的范围和边缘最大流速沿高度基本符合先增大后减小的分布趋势(贴近消力池底板处除外)。关于立轴漩涡的相关研究表明[21],漩涡的切向流速和半径在很大程度上反映了漩涡强度,因此,单侧渐扩消力池内扩散侧立轴漩涡的强涡段均位于漩涡的中部,漩涡强度整体呈“两头小中间大”的分布规律。 对突扩消力池内漩涡的相关研究表明[22],消力池边墙突扩后产生的两个立轴漩涡为椭圆形漩涡,其漩涡的涡心位置略有摆动,但基本固定。由此可见,单侧扩散消力池内的漩涡与突扩消力池中的两个立轴漩涡形状一致,不同的是当单侧扩散消力池的扩散角度较小时,漩涡的游移性强,但随着扩散角度的增大(如方案S5),漩涡位置逐渐趋于稳定。因此可以推断,若单侧扩散消力池的扩散角度继续增大,扩散侧的漩涡将会发展成与突扩消力池相同的立轴漩涡。 图8 各代表性方案不同高度的平面流场分布及漩涡示意图 表2 各选取方案消力池不同高度水平剖面水流漩涡涡心位置 表3 各选取方案消力池不同高度水平剖面水流漩涡强度指标 本文基于物理模型试验,采用RNGk-ε双方程紊流数值模型对单侧渐扩式消力池内的流速和流态进行了计算分析,得出以下结论: (1)三维数值模拟结果与物理模型试验结果吻合度较高,说明采用RNGk-ε方法研究单侧渐扩消力池的水力特性是切实可行的。 (2)采用单侧渐扩消力池布置型式时,消力池底板附近的流速分布不均匀,非扩散侧流速较大,且随着边墙扩散角度的增大,最大临底流速逐渐向非扩散侧偏移,因此设计上要加强对非扩散侧池底的防护。 (3)消力池单边扩散侧的立轴漩涡特性与扩散角度的大小密切相关,随着边墙扩散角的增大,扩散侧逐渐出现贯穿性立轴漩涡,且漩涡空间尺度变大,漩涡位置趋于稳定。 (4)消力池内漩涡强度沿高度的分布规律类似,强涡区均出现在漩涡中部,整体呈现“两头小中间大”的分布规律。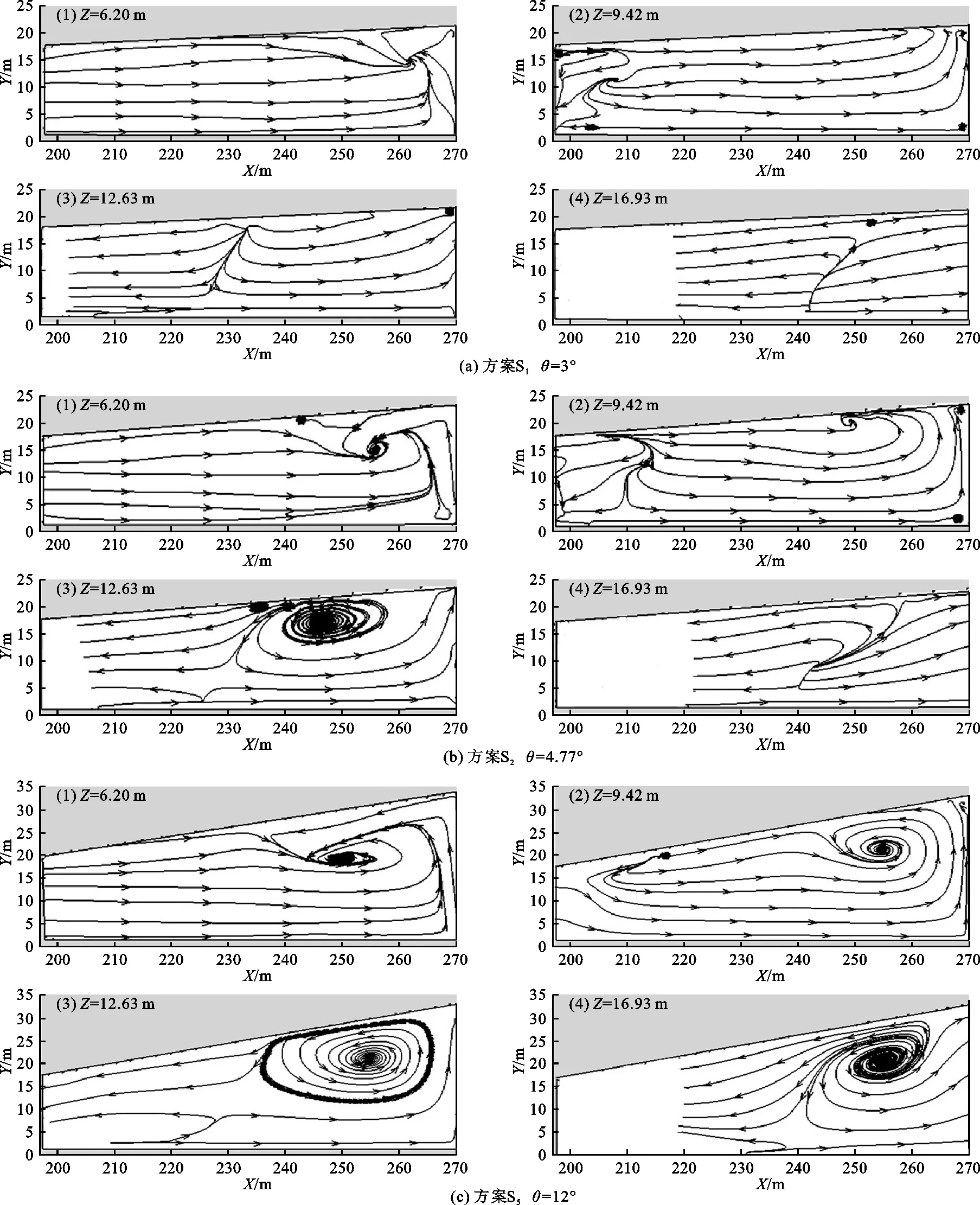
4 结 论
——辽宁省博物馆藏中国古代立轴山水画展

