基于正交试验法的河岸带水热耦合模型敏感参数识别
李昱春, 张文兵, 任 杰, 李舸航, 甘 磊, 徐力群
(1.苏州市吴中区水务局, 江苏 苏州 215128; 2.上海海事大学 海洋科学与工程学院, 上海 201306;3.河海大学 水利水电学院, 江苏 南京 210098; 4.西安理工大学 水利水电学院, 陕西 西安 710048;5.上海市堤防泵闸建设运行中心, 上海 200080)
1 研究背景
近年来,随着河长制、湖长制以及长江大保护等一系列重大战略举措的推行,我国对于河流的保护、治理和管理进入了新的发展阶段,对江河湖泊水域岸线的管理保护提出了更高的要求。河岸带作为河流生态系统与陆地生态系统的过渡带,对削减河流污染、调蓄洪水和保护水土环境具有重要作用,同时它也是动植物生长和栖息的重要场所[1-3]。因此,针对河岸带相关问题的研究受到越来越多学者的关注,并成为生态环境水力学研究中的热点[4-6]。
河岸带地下水与河流地表水时刻发生着能量的交换,温度作为能量的直观载体,是理想的天然示踪剂[7]。目前,已有众多学者将温度示踪法应用于河流地表水与地下水交换速率及过程模式的研究中[8-13]。有关温度示踪法应用于河岸带相关问题的研究已有大量报道,但多侧重于试验手段。随着河岸带水热耦合理论研究的深入,通过建立水热耦合模型的数值方法来研究河岸带内部水热动态变化过程成为一种重要手段,例如,张文兵等[3]构建了考虑土体非均质传热的河岸带水热耦合模型,对比了不同土体有效导热系数模型下河岸带水热耦合模型的模拟效果;Ren等[14]利用洞庭湖河岸带某典型断面的温度和水位监测资料,验证了所建立的水热耦合模型的合理性。然而,河岸带水热耦合模型涉及诸多参数,参数反演分析比较困难,同时也会给模型的应用增添较多的校正工作。因此,开展河岸带水热耦合模型参数敏感性研究有利于快速确定相关参数的取值,为模型参数的校准提供参考,对模型在实际工程中的广泛应用具有重要意义。
现有的敏感参数识别方法大致可分为单因素分析法和多因素分析法两种。单因素分析法多适用于模型参数较少的情况,并且该方法假设模型参数之间无相互作用,而这一假设与实际情况不符[15]。相较之下,多因素分析法则弥补了单因素分析法的不足,能够更加准确、全面地反映敏感参数识别结果。在利用多因素分析法进行敏感参数识别时,若对参数进行全面组合,会带来较大的工作量,正交试验设计则可以避免多因素试验的全面组合,并且能够寻求最优的参数组合来反映试验结果。为此,本文采用正交试验方法来识别河岸带水热耦合模型的敏感参数,以期为河岸带水热耦合模型参数选取、校正及应用提供参考。
2 资料来源与研究方法
2.1 研究区域概况
沃克湖(Walker Lake)是美国内华达州西部的一个重要水源,为当地的农业提供用水,并为当地多个社区使用的地下水含水层补水。沃克湖是大盆地中为数不多的多年生天然终端湖泊之一,终端湖泊是地形封闭盆地中地表水排水的终点。在自然条件下,湖面的蒸发量通常是湖水流出的全部组成部分。由于大盆地的高蒸发率,终端湖泊的水位和盐度对河流流入的变化极为敏感。19世纪60年代开始,为了支持日益增长的农业发展,当地农耕者开始从沃克湖引水。随着时间的推移,从上游水库和引水口流入沃克湖的水量减少,导致湖面下降了51.816 m,因此,沃克河流域的大部分水流只能来自内华达山脉的融雪,但这也导致水体中总溶解固体(total dissolved solids, TDS)浓度大大增加,严重威胁水生生态系统的平衡,包括濒危物种拉洪顿鳟鱼的生存。由于消耗性用水,沃克湖和大盆地的其他终端湖泊的生态系统已处于危险之中。为此,美国地质调查局自2012年3月至2013年10月在沃克湖流域进行了广泛的实地研究,以量化史密斯谷、梅森谷和沃克湖谷灌溉区相关河流的渗漏损失。图1为沃克湖流域图。

图1 沃克湖流域概况
2.2 数据来源
本文数据主要来源于美国沃克河流域2012年4月至2012年6月相关河流的水位及温度变化数据。该部分数据公开于美国地质调查局官网,允许研究人员下载获取(网址:https://pubs.er.usgs.gov/publication/sir20165133)。
2.3 研究方法
2.3.1 河岸带水热耦合数学模型 河岸带饱和-非饱和瞬态渗流场采用Richards方程描述[16]:
(1)

水力特性对饱和度和压力的依赖性导致Richards方程的高度非线性,因此,学者们提出了各种数值和分析方法用于评估Richards方程,而最常用的是通过土壤水分特征曲线(soil water characteristic curve,SWCC)来研究水力特性。迄今,在用以描述土壤水分特征曲线的经验公式中,具有代表性的有van Genuchten模型[17]、Gardner模型[18]和Brooks-Corey模型[19]。在众多的模型中,van Genuchten模型具有精度高、参数物理意义明确、适用性较强[20-21]的优点,其对负压Hp<0(即非饱和条件)下水力特性的解析定义为:
θ=θr+Sr(n-θr)
(2)
(3)
(4)
kr(θ)=Sr1/2[1-(1-Sr1/m)m]2
(5)
式中:θr和θs分别为残余与饱和体积含水率,m3/m3;n为孔隙率;hp为压力水头,m;α和β为与SWCC曲线有关的van Genuchten模型参数;m为与β相关的参数,m=1-1/β。
值得注意的是,当Hp≥0时,假定θ=n,则有Sr=1,Cm=0和kr(θ)=1,方程式(1)将自动转化为完全饱和的达西方程。因而,对于河岸带整体模型而言,该方程既能考虑河岸带中饱和土体的水流运动,又能考虑河岸带上覆非饱和土体的水流运动。
采用对流-传热方程描述河岸带水体与土体间的热量交换[22]:


(6)
式中:Cw、Cs分别为水与土体的体积热容,J/(m3·℃);λe为土体有效导热系数,W/(m·℃);DH为水动力弥散系数,m2/s;u为平均流速,m/s;Qs为热量源汇项,W/m3。
方程式(6)中的水动力弥散系数DH可表示为:
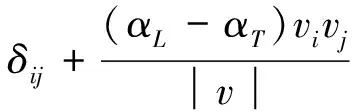
(7)
式中:αT和αL分别为横向和纵向弥散度,m; |v|为流速矢量的大小,m/s;δij为克罗内克尔二阶单位张量;vi、vj分别为速度矢量的第i个和第j个分量,m/s。
同样地,当孔隙处于饱和状态,则θ=n,方程式(6)退化为饱和含水层对流-传热方程。
由于土体有效导热系数在干燥状态和饱和状态下差异较大,仅设定为固定常数是不准确的,为此引入土体有效导热系数经验模型用于反映因含水率不同导致的非均质参数空间分布问题。目前,有关土体有效导热系数预测的经验模型众多,其中Johansen土体有效导热模型能够较好地反映河岸带土体非均质传热[3],其表达式为:
λe(θ)=(λsat-λdry)Ke+λdry
(8)
式中:λsat和λdry分别为饱和与干燥状态的土体导热系数,W/(m·℃);Ke为归一化导热系数。这些系数的计算如公式(9)~(11)所示。
(9)
(10)
(11)
式中:λw为水的导热系数,W/(m·℃);λs为土体的导热系数,W/(m·℃);λs由土体中的石英含量(q)及其导热系数(λq=7.7 W/(m·℃))和其他矿物的导热系数(λ0)计算得到,即λs=λqqλ01-q(当q>0.2时,λ0=2.0 W/(m·℃);当q≤0.2时,λ0=3.0 W/(m·℃));ρb为土体的堆积密度,kg/m3。
2.3.2 敏感性分析 正交试验法是从大量的试验点中选取部分具有代表性的点进行多因素试验,可以大大减少试验次数,减少工作量,目前已广泛应用于科学试验研究[20,23-26]。正交试验表是正交试验法的核心,以“七因素三水平”情况为例,其正交试验表可参考文献[15]进行设计。
极差分析法和方差分析法是分析正交试验结果的两种常用方法。相较于方差分析法,极差分析法难以区分影响试验结果变化的因素,并且只能给出各因素的影响次序,而无法定量判断该因素的敏感程度[24]。方差分析法则能较好地估计试验误差的大小,并且能够反映模型结果输出对各参数敏感程度的量化结果。方差分析法的基本原理如下:
以Ln(rc)试验为例,将第k次试验的结果记为Yk(k=1, 2, ···,n),令Tij为第j列因素第i个水平试验结果Yk之和,T为总试验结果之和,pij为因素j在i水平下的试验次数,则:
(12)
(13)
pij=n/r
(14)
(15)
将试验中n个试验结果的总变差记为ST,表示全部试验结果之间的差异程度;第j列变差平方和记为Sj,表示第j列因素不同水平之间的差异程度;总和记为Se,表示试验条件的差异程度。则:
(16)
(17)
(18)
假定ST、Sj和Se的自由度分别为fT、fj和fe,则:
fT=n-1
(19)
fj=r-1
(20)
(21)
计算过程中,各试验结果(Y1,Y2,…,Yn)相互不影响,并且服从同方差σ2的正态分布,则可构造F检验的统计量:
(22)
通过将Fj值与F分布表中查找的检验临界值Fα(fj,fe)进行比较,则可以判断模型输出结果对各因素变化的敏感程度。
2.3.3 计算模型 以文献[3]中的工程实例即沃克湖福克斯1号灌渠作为本文的计算模型。
(1)几何模型。福克斯灌渠是美国内达华州沃克湖的支流之一,美国内华达水科学中心的研究人员在此布设有温度和水位监测装置,用于监测该河流地表水与地下水的温度和水位[26]。本文选取福克斯1号灌渠的某河岸带典型剖面进行水热耦合模型敏感参数识别,模型计算范围如图2所示。图2中BP1和BP2分别为距离河道中心2.8和5.8 m的温度测杆,每个测杆内悬挂有3个温度传感器,用于测量河岸带沉积层的温度变化。另外,河道中还布设有温度和水位记录仪用于记录河水温度和水位。环境温度则是由埋设在河岸带表层土体中的温度传感器进行记录。图3给出了福克斯1号灌渠在2012年4-5月的河水温度、水位及环境温度实测变化曲线。
(2)计算参数。本文河岸带水热耦合模型计算参数取自于文献[3]、[27]~[29]中给出的相关参数,具体数值见表1。

图2 模型计算范围示意图[3](A~F为边界编号)

图3 2012年4-5月福克斯1号灌渠河水温度、水位及环境温度实测变化曲线

表1 模型计算参数
(3)边界条件及初始条件。对于河岸带渗流场,模型左(AF)、右(BC)及表层土体边界(CD和EF)设为无流动边界;土-水接触边界(DE)设为水头边界;底边界(AB)设为透水层边界。对于河岸带温度场,模型左(AF)、右(BC)及底边界(AB)设为绝热边界;表层土体边界(CD和EF)和土-水接触边界(DE)均设为温度边界,将变化的环境温度和河水温度分别施加于对应的边界上。渗流场的初始条件是将前一时刻实测的压力水头通过线性插值施加于计算域中;温度场的初始条件为各区域模拟前一时刻的实测平均温度。
3 结果与分析
3.1 模型验证
为了验证河岸带水热耦合模型的准确性及定量评价模型的模拟效果,引入均方根误差(RMSE)、决定系数(R2)和相对误差(Re)作为模型评价指标[29]。图4给出了河岸带各监测点温度模拟值与实测值的对比。

图4 2012年4-5月河岸带各监测点温度模拟值与实测值对比
由图4可以看出,基于水热耦合模型模拟得到的河岸带各测点的温度模拟值与现场实测值结果较为吻合,并且具有较好的一致性,表明该模型能够较为准确地反映河岸带水热动态变化过程。为了定量描述模型的准确性,表2给出了河岸带各监测点温度模拟值与实测值对比的评价指标统计结果。
由表2可以看出,河岸带水热耦合模型模拟结果的RMSE值介于0.16~1.67 ℃,R2值介于0.65~0.99,Re值介于1.87%~12.65%,各项评价指标均表现出较好的结果,仅在测点BP2-1.50 m处的结果表现稍差,但亦在指标控制的合理范围内。因此,河岸带水热耦合模型的合理性得到了验证。
3.2 河岸带水热耦合模型敏感参数识别
基于上述河岸带水热耦合模型,将敏感性分析对象定为影响河岸带温度(T)和侧向潜流交换速率(|vx|)所涉及的7个模型参数,具体包括水力传导率(ks)、饱和含水率(θs)、残余含水率(θr)、孔隙率(n)、van Genuchten模型参数(α、β)、土体的体积热容(Cs)。计算过程中,每个参数选取3个水平,各水平分别取自基准值以及基准值分别增减10%以后的数值。考虑到河岸带的范围[30],将敏感性研究区域限定在图2,x∈[5.13, 6.14]且y∈[-2.90,1.10]的模型尺寸范围中,将因参数变动的温度(侧向潜流交换速率)与额定温度(额定潜流交换速率)在对象区域每个有限元单元节点上做差值,然后取平均值来表示温度(侧向潜流交换速率)的变化。
本文选择L18(2×37)正交表设计正交试验,由于只有7个试验因素,故将第1列设为空列,并将各因素的不同水平对应填入,得到识别模型敏感参数的正交表,如表3所示,表3中的每1行即为1组试验工况。

表2 模型评价指标统计

表3 敏感参数识别正交试验方案及试验结果
按照表3设计的试验方案分别计算每种方案下的试验指标T和|vx|,并将它们列在表3的最后2列。根据得到的各组工况下的试验结果,通过方差分析可得到各参数对试验指标的敏感性。
根据方差分析原理,本文选用α=0.10和α=0.05作为显著性检验水平,并将计算所得的统计量Fj与选取的两种显著性检验水平的F值进行比较,从而确定各参数的显著性。这里将显著性水平划分为3个等级:(1) 当Fj>F0.05(2,3)时,表明因素敏感性非常高,影响高度显著;(2)当F0.05(2,3)>Fj>F0.1(2,3)时,表明因素敏感性中等,影响一般显著;(3)Fj 表4 各因素对指标T和|vx|的敏感性分析结果 由表4可以看出,对河岸带温度而言,参数敏感性由高到低依次为n、θs、θr、Cs、ks、β、α,其中孔隙率n对河岸带温度的影响高度显著,即敏感程度高;参数θs、θr、Cs、ks、β、α对河岸带温度的影响不显著,即敏感程度低。对于侧向潜流交换速率而言,参数敏感性由高到低依次为ks、θs、β、Cs、α、n、θr,其中水力传导率ks对河岸带侧向潜流交换速率的影响高度显著,即敏感程度高;参数θs、β、Cs、α、n、θr对侧向潜流交换速率的影响不显著,即敏感程度低。 虽然已有部分学者评估了河岸带水热耦合模型参数对计算输出结果的敏感性[9,26,31],但不同的建模方法和计算方法均会对敏感性分析结果产生影响。Noranjo等[27]使用VS2DH软件对构建的水热耦合模型参数敏感性进行了分析,结果表明水力传导率ks和VG模型参数α是影响模型输出的敏感参数,其中ks是最重要和最敏感的参数。然而,该结果是基于单因素敏感性分析获得,未考虑多参数间的相互作用。Ren等[9]基于HYDRUS-2D构建了室内水槽试验的河岸带水热耦合模型,分析了河岸带水热动态变化过程,并对模型参数进行了单因素和多因素敏感性分析。该研究结果不仅揭示了对模型温度输出敏感的内部因素(水力传导率ks和VG模型参数α),而且研究了水头和温度等外部因素对模型输出结果的影响。在最新的研究中,Ren等[31]采用Morris法对不同土体导热系数模型下的水热耦合模型参数进行了敏感性分析,认为水力传导率ks和孔隙率n对模型输出结果较为敏感。这与他们之前的敏感参数识别结果存在差异,而这种差异可能是由数学模型和导热系数模型之间的差异引起的。因此,不同的建模方法或计算方法可能会对敏感性分析结果产生影响。但是,结合本文的结果,一般来说,水力传导率ks和孔隙率n仍然是最重要和最敏感的参数,这在一定程度上反映了本文结果的准确性。 (1)对于河岸带水热耦合模型而言,孔隙率n是影响模型温度输出的主要参数,水力传导率ks是影响模型侧向潜流交换速率输出的主要参数。其他参数相对这两个指标在模型输出结果中的影响较小。 (2)在对河岸带水热耦合模型参数进行反演分析时,可着重对敏感程度高的参数进行反演,而对于敏感程度较低的参数,则可通过工程类比的方法进行推求,进而提高模型参数的反演效率,并且减少模型校正的工作量。 (3)河岸带水热耦合模型处于不断发展中,未来的模型将更符合实际工程,而模型敏感参数的识别受模型构建方法等因素的影响,需对不同构建方法下的模型参数进行敏感识别,以期为模型在实际工程中的应用提供指导。另外,现有的敏感性分析方法种类繁多,并且模型所涉及的参数越来越多,需考虑发展适用于多参数耦合作用下的敏感性参数分析方法。
4 讨 论
5 结 论

