底吹氩对110 t双透气砖钢包流场影响的数值模拟
刘西峰,李大亮,韩建林,战东平,邹 涛,张慧书
(1.山西建龙实业有限公司,山西 运城 043801; 2.东北大学 冶金学院,辽宁 沈阳 110819;3.辽宁科技学院,辽宁 本溪 117004)
洁净钢生产是钢铁行业发展的必然趋势[1-4],随着用户对钢质量要求的越来越高,前人对各种提高钢的洁净度的措施开展了广泛研究[5-7]。其中,钢包底吹氩是均匀钢水成分、温度、促进渣钢反应以及加速钢中夹杂物去除的最有效的手段之一,前人采用水模、数值模拟等方法对钢包底吹氩过程流场、温度场、卷渣及合金化等进行了研究[8-12]。本文以某钢厂110 t LF 精炼炉用钢包为原型,在前期物理模拟的基础上[13],利用 Fluent 软件进行数值模拟,研究双透气砖布置形式对钢包流场的影响,为企业的生产实践提供指导。
1 钢包底吹氩数值模拟的数学模型
1.1 数值模拟的基本假设
气泡上浮过程中,对钢水所做的功是钢包内流体循环流动的唯一动力,气液两相区的形状是锥形区域;气液两相区按变密度单相来处理,吹气过程中,两相区的含气率由实验关系式确定;忽略温度和表面渣层的影响。
1.2 控制方程
描述钢液在钢包底吹气的方程有连续性方程、动量方程,能量方程以及确定紊流黏性系数的k-ε双方程模型[14]。
1)连续性方程
(1)
2)动量方程
(2)
3)湍流模型方程(标准k-ε双方程模型)
k方程:
(3)
ε方程:
(4)
4)能量守恒方程
(5)
式中:Γeff为有效热扩散系数;ui,uj为湍流流动的时均速度,m/s;ρ为流体(钢液)的密度,kg/m3;k为湍流脉动动能,m2/s2;ε为湍流脉动动能耗散率,m2/s3;P为压力,N/m2;μeff为有效黏性系数,kg·s·m-2;μt为湍流黏性系数,kg·s·m-2;gi为i方向上的体积力,m/s2;σt为层流Prandtl数;σt,T为湍流Prandtl数;μl为层流黏度系数;μt为湍流黏度系数;μ为 流体(钢液)的动力黏度,kg/m·s。C1=1.44,C2=192,Cμ=0.09,σk=1.0,σε=1.3。
1.3 计算步骤
在Fluent的前处理软件Gambit中建立钢包模型,并划分网格,钢包及计算用网格如图1所示。将得到的网格导入Fluent中,进行流场、均混时间以及温度场的计算。计算步骤为:选择非耦合求解,求解方程选择标准的k-ε双方程,钢液表面设置为滑移边界,材料物性参数密度的变化通过UDF实现,采用SIMPLE算法,然后迭代计算流场,当流场计算收敛后,运用能量守恒方程计算温度场,最后加入传质方程计算均混时间。

图1 钢包及网格划分
1.4 模拟方案
数值模拟根据钢厂双透气砖的生产使用情况,分别计算了钢包原布置方案A(0.5r-0.5r)以及2种新布置方案B(0.4r-0.5r)和方案C(0.4r-0.4r)的条件,同时分别模拟这3种布置方案在100 L/min(标准,软吹)、200 L/min(标准,中吹)、450 L/min(标准,硬吹)条件下流场的变化情况。
2 钢包流场数值模拟计算结果
2.1 100 L/min(标准,软吹)条件下的钢包流场特征
图2~图4分别为三种方案在100 L/min(标准,软吹)气量下的流场分布图。从图2和图4中可以看出,当透气砖对称分布时底吹气形成的气柱也成对称分布,两股气体对各自存在的半个熔池都可以起到搅拌作用;如图3所示的即为底吹透气砖不对称布置时的流场分布。从图3中可以看出,由于透气砖的不对称分布,使得靠近钢包底部中心的一边气流受到远离中心气流的影响,向远离中心的一股气流处发生偏移,从自由液面的速度分布图也可以看出,两股气流的搅拌并不均匀,这种情况是底吹透气砖布置所不希望看到的情况,因此不建议采用诸如方案B的底吹透气砖不对称布置方式。
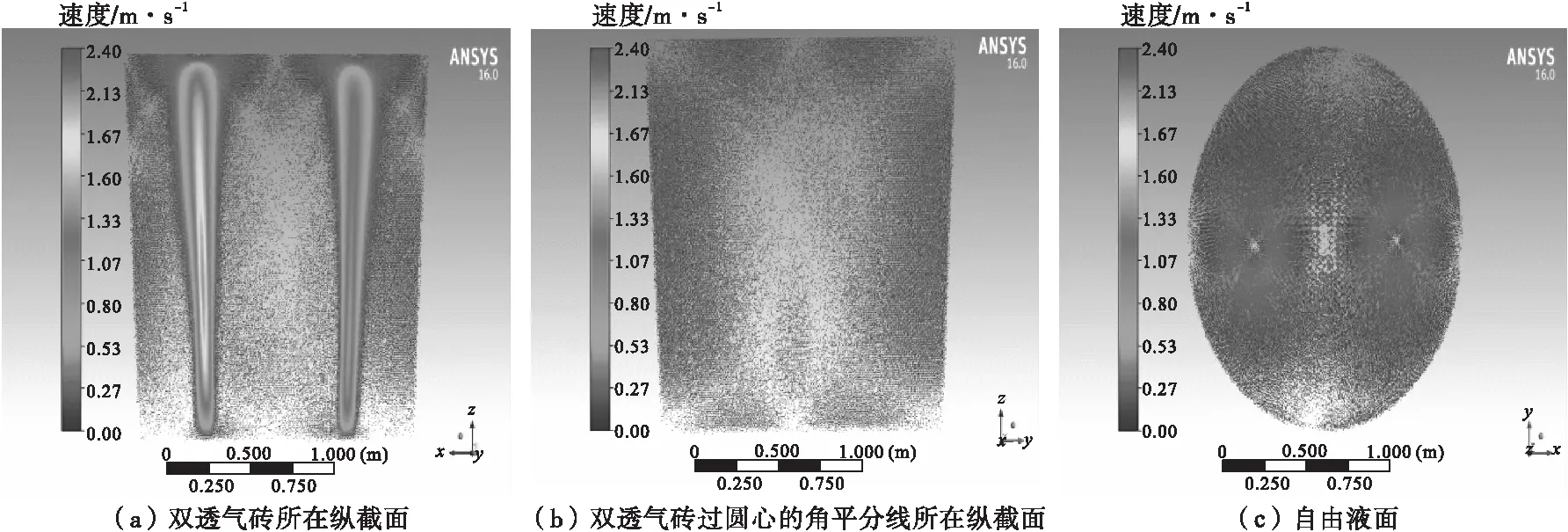
图2 100 L/min(标准)气量下方案A透气砖布置时的流场图

图3 100 L/min(标准)气量下方案B透气砖布置时的流场图
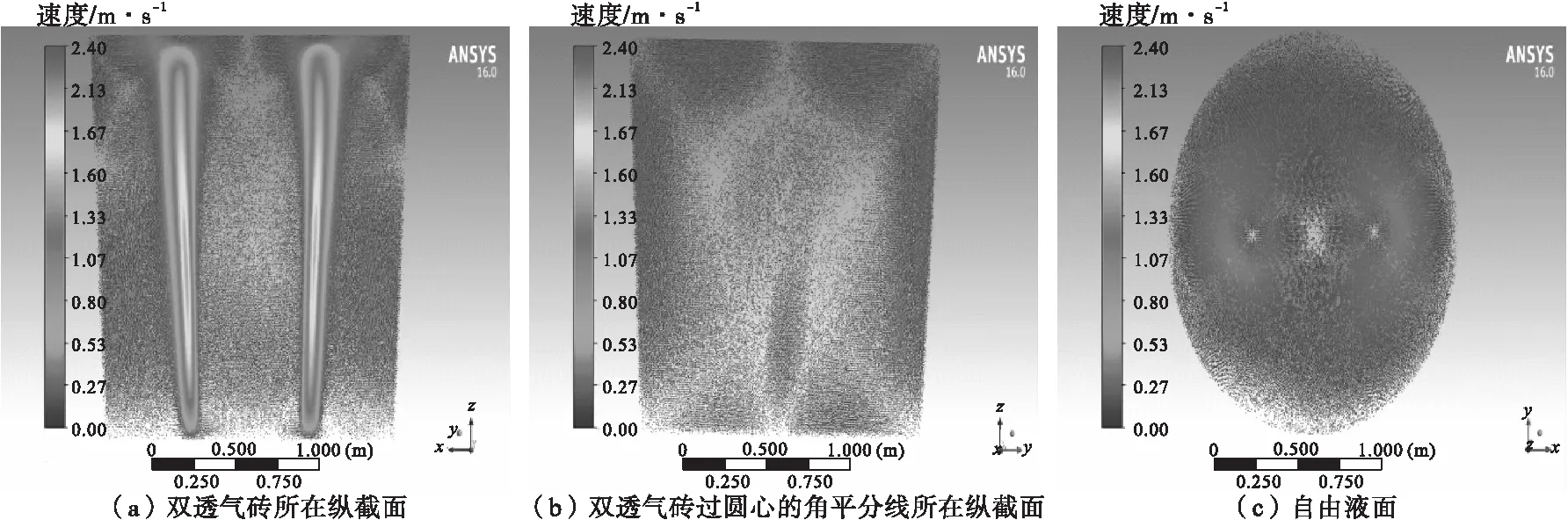
图4 100 L/min(标准)气量下方案C透气砖布置时的流场图
另外,分别观察图2和图4自由液面的速度分布图可以发现,对于方案A来说由于透气砖布置的位置相对于方案C来说更靠近钢包壁面,因此气柱向上运动时会对钢包内壁产生冲刷,导致气柱所携带的动能有所损失,从而直接导致从自由液面看上去明显发现原方案A气柱所影响的范围相对于方案C小很多,因此原方案A的搅拌效果也会较方案C下降很多;再从图2与图4的双透气砖所在纵截面上可以看出,由于方案C相对于原方案受到包壁影响较小,因此可以发现方案C的气流中心的速度要大于原方案的气流速度,这也加快了夹杂物的上浮,提高了搅拌效率。
2.2 200 L/min(标准,中吹)条件下的钢包流场特征
图5~图7分别为三种方案在200 L/min(标准,中吹)气量下的流场图。从图5和图7可以看出,底吹透气砖处于对称布置的流场来说,自由液面处两股气流分别对各自存在的半个熔池的影响是相同的;而对于如图6所示的方案B这种不对称分布的流场来说,靠近钢包底部中心的气流会偏向远离中心一侧的气流,这样就会使得气流对于熔池的搅拌不均匀。

图5 200 L/min(标准)气量下原方案A透气砖布置时的流场图
选择底吹透气砖对称分布时,如图5和图7所示原方案A和方案C的流场分布图,首先观察两种方案的自由液面,可以发现,同样原方案A由于对钢包内壁的冲刷作用,使得气柱的动能有所损失,从而导致原方案的气柱所影响的熔池范围会小于方案C气柱所影响的熔池范围,尤其是过双透气砖圆心连线的角平分线所在纵截面,越靠近包壁处,原方案所产生的影响就越小,然而方案C所产的影响却要大于原方案A所产生的影响;同样在双透气砖所在纵截面也可以看出,方案C气柱中心的速度要大于原方案气柱中心的速度。
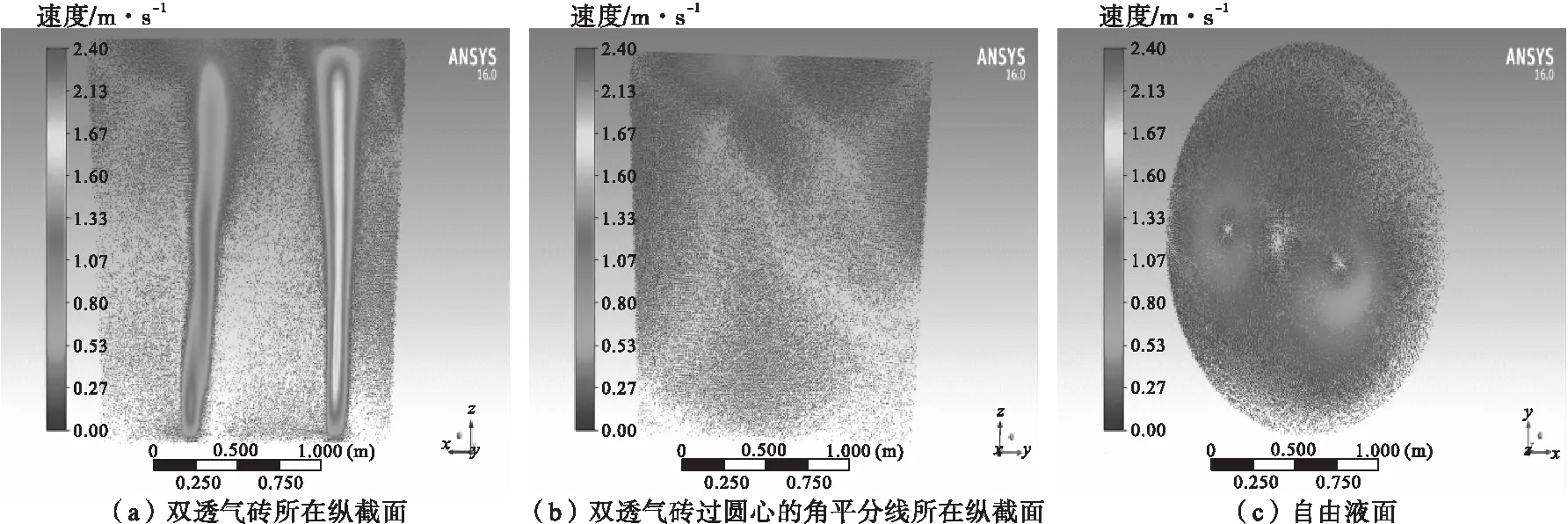
图6 200 L/min(标准)气量下方案B透气砖布置时的流场图
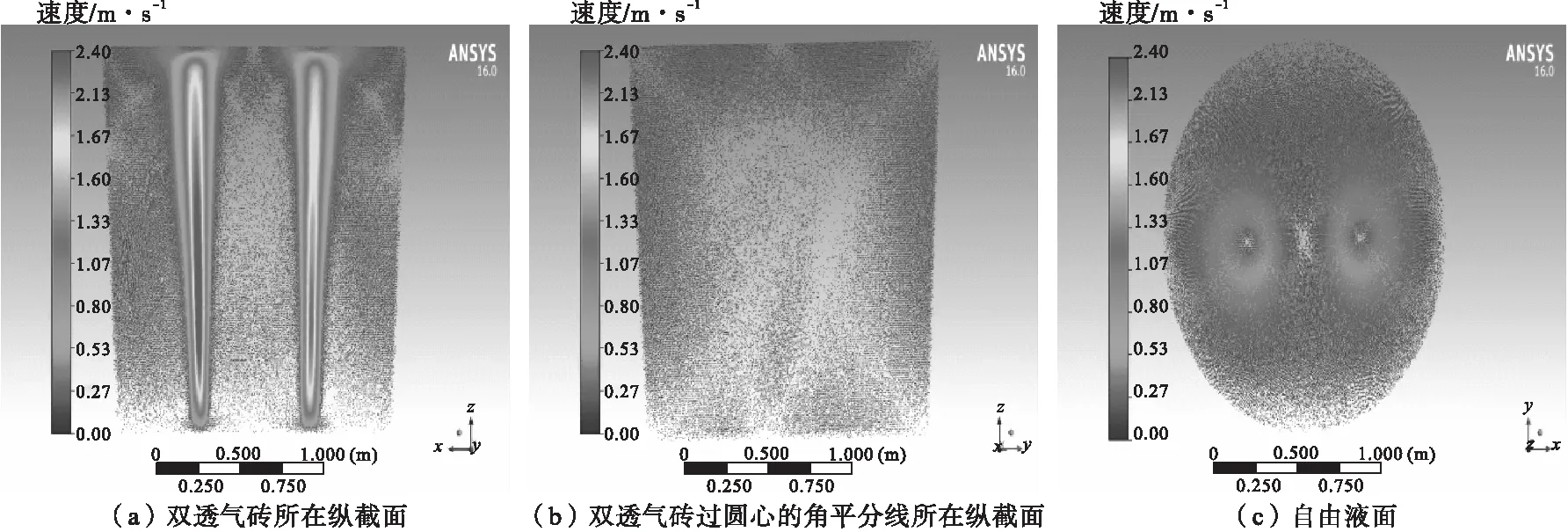
图7 200 L/min(标准)气量下方案C透气砖布置时的流场图
2.3 4 500 L/min(标准,强吹)条件下的钢包流场特征
图8~图10分别为三种方案在450 L/min(标准,强吹)气量下的流场图。当流量处于硬吹区时,由于气体的动能较大、流速较快,如图9所示的方案B底吹透气砖不对称分布时,两股气柱之间的相互影响也减弱得很多,但是依然由于气柱上升过程中需要克服两股气流之间的相互作用力,导致气流的动能有所损失;而对于图8和图10所示的原方案和方案C来说,由于底吹透气砖是对称分布的,因此两股气流之间的相互作用力相互平衡,因此气柱在上升过程中无需过多的克服气流之间的相互作用力,因此如图8和图10所示的原方案和方案C在双透气砖所在纵截面上的气流中心速度都要较方案B气流中心速度大且均匀。

图8 450 L/min(标准)气量下原方案A透气砖布置时的流场图

图9 450 L/min(标准)气量下方案B透气砖布置时的流场图

图10 450 L/min(标准)气量下方案C透气砖布置时的流场图
综上所述,在对所设定的原方案A(0.5r-0.5r)、方案B(0.4r-0.5r)和方案C(0.4r-0.4r)的流场比较中,方案C(0.4r-0.4r)的流场更为合理,更有利于夹杂物的快速上浮以及钢包内成分的均匀化。
2.4 最佳钢包底吹位置的确定
通过所得出的数模结果可以很好反映实际实验情况的结论,下面对于数模结果分析探究最佳钢包底吹位置。图11为数模条件下不同位置均混时间的比较结果。可以看出,当方案B透气砖布置在0.4r-0.5r这种不对称位置分布时,在不同的气体流量区,均混时间变化较大,随着气体流量的增大均混时间呈现先减小后增大的变化规律;而对于方案C(0.4r-0.4r)和方案A(0.5r-0.5r)对称分布时,均混时间是随着气体流量的增加而减少的。因此,同样在对底吹气透气砖布置时不建议采用非对称布置。
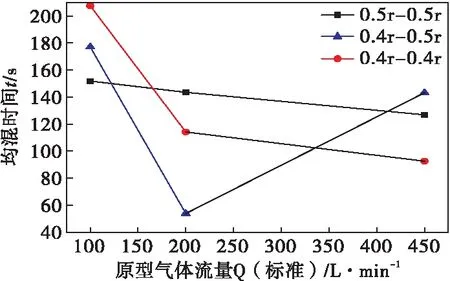
图11 数模不同位置均混时间比较
再对方案C(0.4r-0.4r)和方案A(0.5r-0.5r)的布置进行比较可以看出,尽管在软吹区方案C(0.4r-0.4r)布置所得到的均混时间要大于方案A(0.5r-0.5r)布置得均混时间,但是在软吹区的末端以及进入中吹区开始时,均混时间开始大幅度降低,从此开始随着气体流量的增加方案A(0.5r-0.5r)和方案C(0.4r-0.4r)布置所得到的均混时间均发生均匀下降,但是对于方案C(0.4r-0.4r)的布置所得到的均混时间始终小于方案A(0.5r-0.5r)布置所得到的均混时间。
3 结 论
(1)双透气砖非对称布置的方案B(0.4r-0.5r),靠近钢包底部中心的一边气流受到远离中心气流的影响,向远离中心的一股气流处发生偏移,两股气流的搅拌不均匀,因此不建议采用方案B的非对称布置方式。
(2)双透气砖对称布置时,随着吹气量从软吹模式增加到强吹模式,均混时间缩短,且方案C(0.4r-0.4r)的布置所得到的均混时间始终小于方案A(0.5r-0.5r)的均混时间。
因此,在对200 L/min(标准,中吹)气量下的流场图的比较中,方案C(0.4r-0.4r)的流场效果更佳。
(3)方案C(0.4r-0.4r)的流场更为合理,更有利于夹杂物的快速上浮以及钢包内成分的均匀化。

