普通高中人教A版新旧教材统计内容的对比
——以“正态分布”为例
⦿西华师范大学 数学与信息学院 梁 馨 冯长焕
1 引言
21世纪以来,我国开启了新一轮中小学课程的改革.在新课改中,作为课程的重要载体,课堂教学的基础和教师教学与学生学习的材料,教材也在根据课程改革的思想及其对应课程标准的变化而不断改进.当前全国高中数学中普遍使用的两版教材分别是由人民教育出版社出版的2004年版和2019年版,分别对应2001年[1]和2017年[2]颁布的高中数学课程标准.
新课标《普通高中数学课程标准(2017年)》自发行以来就在数学教育界引起了轰动,是每一位数学师范生、一线数学教师和数学教育研究者共同关注和学习的内容.其中正态分布作为现实生活中最常见的统计分布.也是与学生的实际生活最接近的统计分布,更是高中阶段统计内容的重要组成部分.
2017年新课程标准改革后的新教材,相较于前一版的教材,在正态分布这一节的内容上有了较大的改变,包括教材所处的位置、教材知识的引入、教材概念的定义以及教材习题的给定上都有所不同.
新课程标准与现行的课堂教材之间的脱节,对一些地区的师范生和教师而言,在没有经历专门培训的前提下,教师很难把握新课标要求与旧教材使用之间的平衡.因此笔者希望以对比普通高中人教A版教材中的正态分布内容为例,明晰教材变化的原因、新教材的特点,帮助教师如何使用新教材开展新课堂.
2 新旧课程标准的对比
每个学科的课程标准,是制定课程的规范、是教材编订的依据,也是最先准确反应学科课程的改革.数学学科也是如此,每一版高中数学课程标准准确地反应了当时的新课程改革需要,也为新教材的编制提供指南[3].因此,在对比教材内容之前,可以从课程标准中的对应内容进行分析.
新旧两版高中数学课程标准对于“正态分布”一节内容所处的位置的安排如下表1:
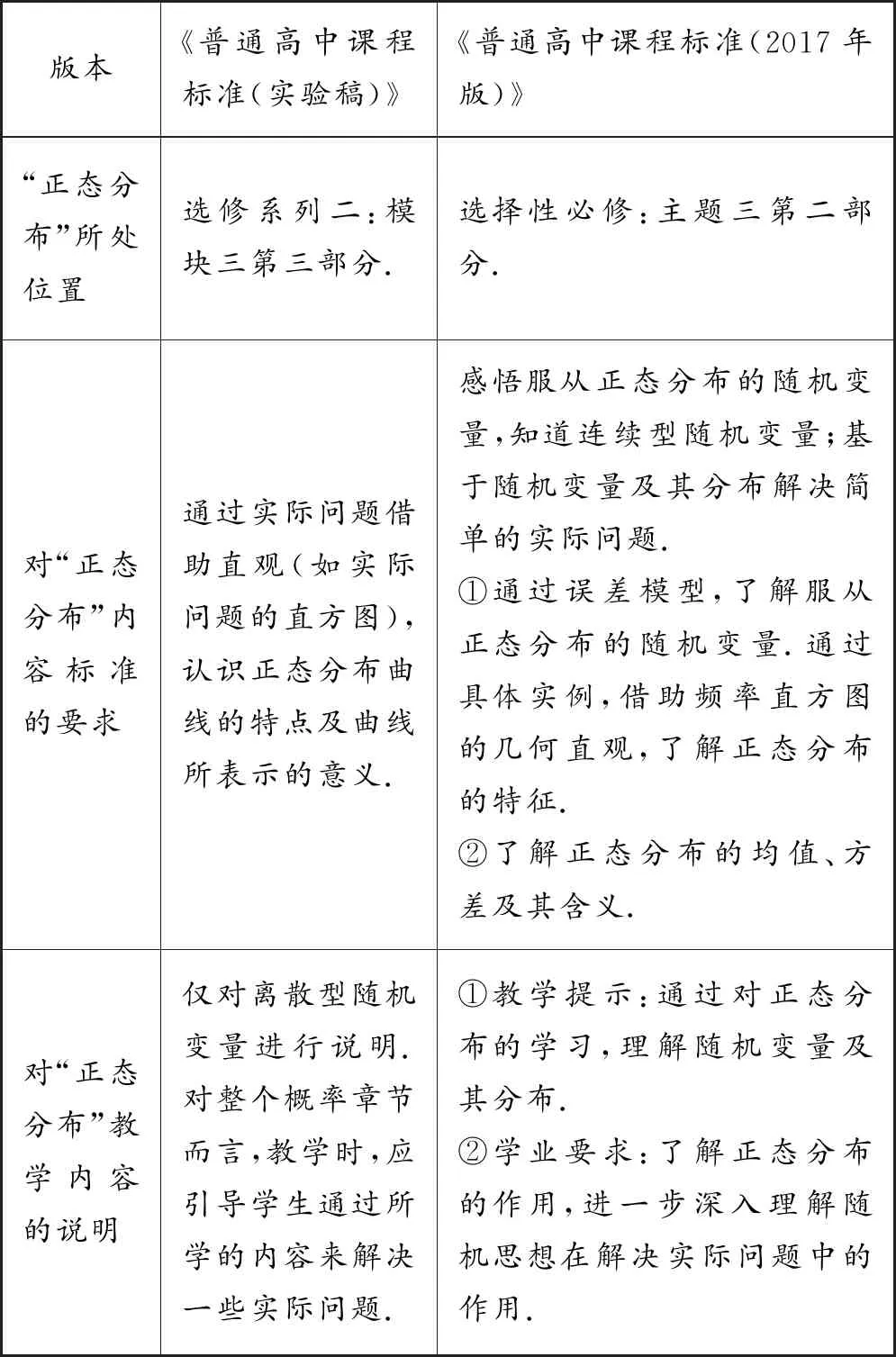
表1
从上表中可以看出,2017年版的高中数学课程标准中“正态分布”内容在所处位置、标准要求和详细说明上都有一定的区别.首先,新版课标将“正态分布”内容归于选择性必修部分,意味着不论学生未来的发展是偏人文学科还是理工科,只要参加高考进入高校学习,都需要对这个常见的连续概率分布有一定的认识和理解.其次,新版课标对于“正态分布”的教学内容的标准有了更加详细和深入的要求.要求从现实实践出发,抽象出数学模型,在对模型进行分析过程中了解服从正态分布的随机变量;在此基础上还希望学生了解连续型随机变量的均值、方差等.再者,新版课标对“正态分布”标准要求的说明,也进行了细化,分别从教师和学生两方面阐明了“正态分布”的教与学需要达到的层次.新旧两版课程标准对“正态分布”这一节的要求不同,自然对于教材的编写要求与建议就有所不同.对比新旧两版课程标准的教材编写建议如下表2:
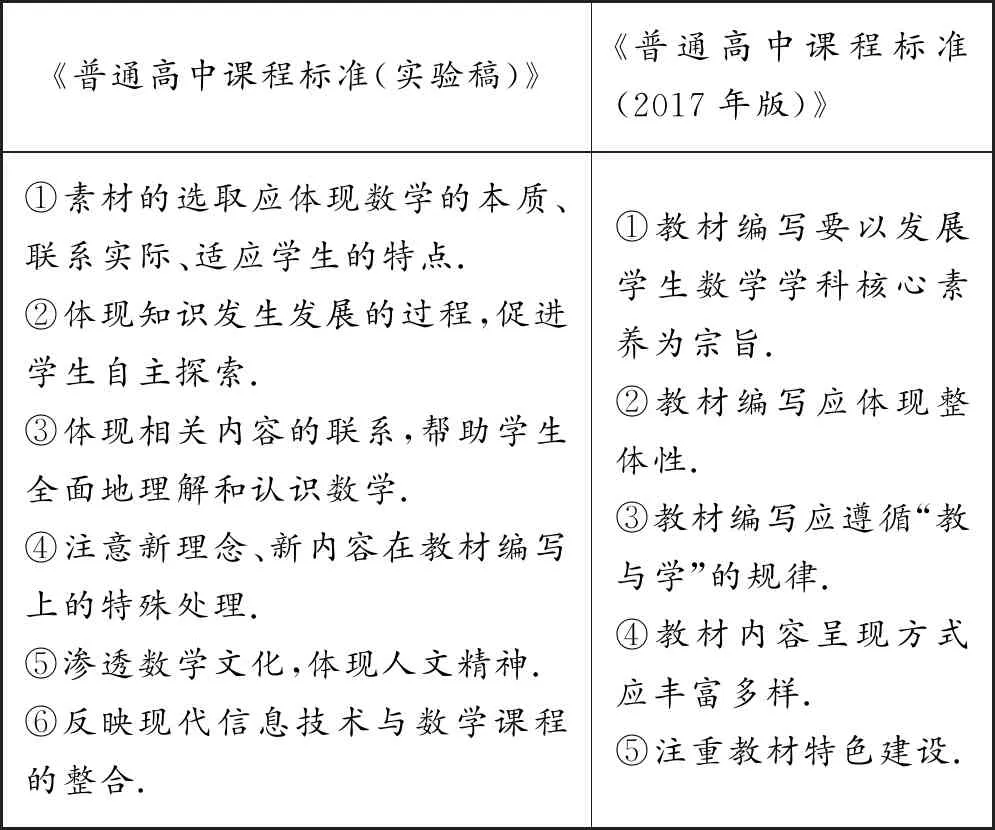
表2
从上表我们可以看出,新版的课程标准更加注重“以人为本”精神,将学生的发展放在首位.同时,兼顾数学学科内部逻辑发展的规律,要求数学知识应遵循整体性的特点.由于多年以来数学教育界的各种理论发展较为成熟,多种理念和方式方法涌现,教材在处理知识的时候遵循“教与学”规律的前提下,应丰富呈现方式和体现特色.
在此基础上,不难看出在《普通高中课程标准(2017年版)》对于“正态分布”内容更加重视,其中不仅反应了统计与概率内容需要成为大众基础知识的社会需要,更是一个社会公民所需要掌握的储备知识,是认识世界上诸多现象的规律之一.在此课标指导下的新版教材,相较于前一版本也必然有所不同.
3 新旧教材内容对比
3.1 教材结构对比
新版教材的选修内容将不再区分文科和理科,所有的内容都囊括入选择性必修教材当中.“正态分布”一节的内容区别于之前的旧版教材位于理科选修2-3的第二章第四节,新版教材的选修第三册第七章“随机变量及其分布”的第五节.章节内部的顺序除了“正态分布”位于最后一节之外,都有些许不同,如下表3所示:
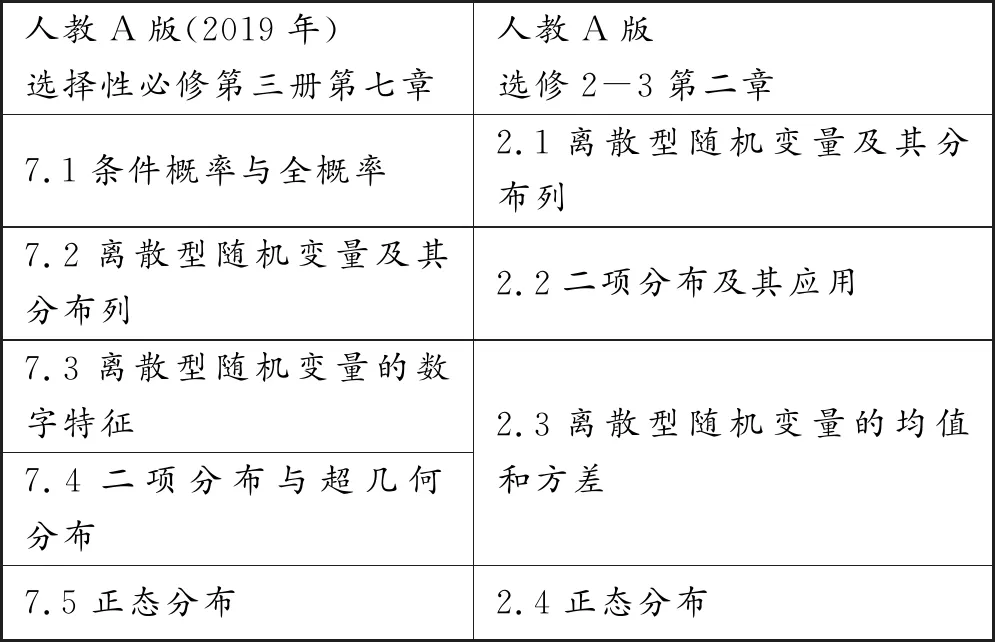
表3
章节顺序的调整源于课程标准对于数学学科内部整体性的要求,使得“随机变量及其分布”这一章更加“科学”.同时,也反映了人们对于统计与概率知识的接受能力与日俱增.但毫无疑问的是,“正态分布”作为高中数学中唯一接触的连续型随机变量,对于学生的学习是一个巨大的挑战,因此把这部分内容放在最后一节,是符合学生的最近发展区理论的.
3.2 教材内容对比
新旧两版教材在“正态分布”一节的内容编排如下图1、图2所示:
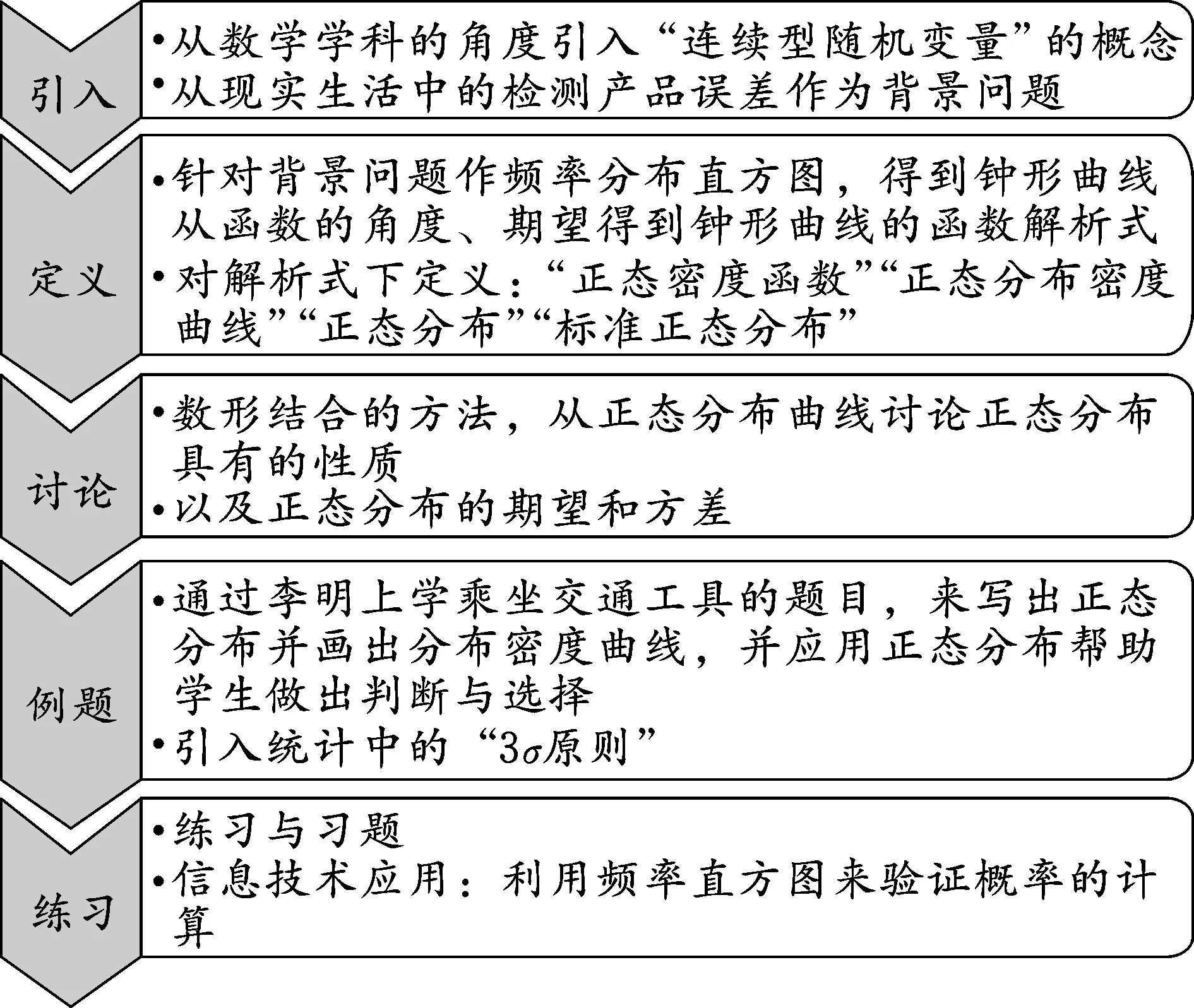
图1 新版教材“正态分布”一节的内容编排

图2 旧版教材“正态分布”一节的内容编排
从以上两图可以看出,新教材在引入“正态分布”一节中,不仅改换为采用与实际生活更加贴切的误差模型作为引入背景,还在章节内容开头就声明了本节学习与之前离散型随机变量不同的连续型随机变量.开门见山,提示了本节与前面内容的不同之处.区别于旧版教材高尔顿试验与现实脱节的情况,体现了章节内容之间的衔接性.
在给“正态分布”下定义时候,新版教材直接通过钟形曲线及其对应的函数解析式,简明扼要地定义了“正态密度函数”“正态分布密度曲线”“正态分布”“标准正态分布”.旧版教材虽然也从图象得出了“正态分布密度曲线”,但是从分布函数的角度定义“正态分布”的.对于分布函数的定义没有事先给出,因此对正态分布密度函数求积分不便于理解.
在讨论“正态分布”性质时,新版教材基于利用数形结合法研究函数的角度,从一般讨论函数的基本性质(单调性、最值、奇偶性等)出发研究正态分布的性质.此外,从函数图象的平移和已有性质出发,讨论了正态分布密度曲线随μ,σ的变化而变化的特点,发现正态分布密度曲线的集中程度和离散程度与μ,σ有关,进而给出正态分布的的期望和方差.而旧教材在讨论正态分布密度曲线性质时,分别从纯图象和纯函数的方面去分别讨论,尤其是在纯函数讨论的时候将μ,σ看成关于函数的一个双参数分别讨论.
此外,新版教材新增一个更加贴近学生日常生活的例题,让学生在认识到正态分布作为现实中最为常见的随机变量之外,还让学生能应用正态分布对随机事件作出判断和选择,体验数学的功用.
新版教材在“正态分布”一节的练习与习题中,更侧重“应用题”,也就是说重视正态分布在实际生活中的应用与思考.
在拓展部分,对于概率与统计的内容向来是需要信息技术手段来处理数据的,这也是补充教材编写如有遗漏的情况.新版教材的编写较为完善,提出可以通过GeoGebra软件,直观地观察已学习的各种分布的概率分布图,感受连续型随机变量与离散型随机变量的不同.而旧版教材由于对μ和σ变化从而影响正态分布密度曲线的讨论不太详细,所以提出通过几何画板的动态变化,来验证上述所讨论的性质.
经过上述的对比分析,不难看出,在新的高中数学课程标准的指导下,“正态分布”这一节的新版教材在编排和呈现方式上,有了较大的不同.总的来说,“正态分布”的内容变得生活化,其本身内容的表述更加简洁.对于“正态分布”的要求也不再只是停留在知道、了解的程度,而是通过简化定义的表述,为后续讨论其性质奠定基础,从而对“正态分布”的理解更加深入——包括在数学学科内部,关于“正态分布”知识的深入了解和在现实生活中,意识到数学是一门来源于实际研究又应用于实际,帮助人们作出判断的“工具”.
4 结论
“正态分布”作为高中数学阶段,唯一遇到的连续型随机变量,为日后更系统地学习概率分布知识奠定了良好的基础,是作为一种先行组织者材料而存在的.同时,作为现实中存在最为广泛的随机变量分布,在沟通数学与现实之间的关系上具有得天独厚的优势[4].新课改、新课标注意到了这一点,因此在新教材关于“正态分布”的编写上做出了较大的改动,使之更贴近实际生活,对于知识的学习也更加深入.
因此,在新旧两版教材过渡阶段,教师可以对比新旧教材在同一内容的不同编排和不同的呈现方式,辅助新旧两版的课程标准,感悟新教材的“新”地方,进而把握教材更替的平衡,提高自身的教学水平.

