CRTS Ⅱ型板式无砟轨道水平推板试验及仿真

刘学文， 谷永磊， 刘钰

（1.京沪高速铁路股份有限公司，北京 100038；2.京沪高速铁路股份有限公司 设备安全部，北京 100038；3.西南交通大学 土木工程学院，四川 成都 610031）

0 引言

CRTS Ⅱ型板式无砟轨道结构主要由钢轨、扣件、轨道板、水泥乳化沥青砂浆（简称CA 砂浆）层和底座板/支承层等组成［1］，轨道板和底座板/支承层为钢筋混凝土和混凝土材料，两层之间由CA 砂浆填充、固化，形成多层异质材料复合薄板结构（见图1）。CA 砂浆层与轨道板和底座板/支承层之间的界面保持良好黏结性能，是CRTS Ⅱ型板式无砟轨道结构保持稳定性和耐久性的关键。层间界面黏结不均匀或不充分将影响结构层间应力分布状态和传递规律。在温度反复作用及列车荷载循环冲击下，层间界面一旦发生黏结失效，因界面应力不连续、不均匀引起的应力集中必然导致层间离缝进一步发展［2］，造成轨道结构出现不可修复的破坏甚至失稳，危及轨道服役安全。

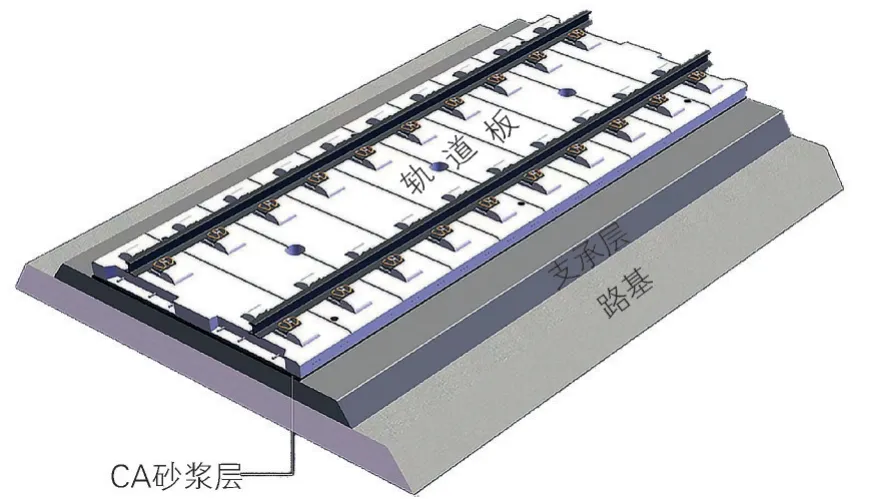
图1 CRTS Ⅱ型板式无砟轨道结构示意图

为掌握CRTS Ⅱ型板式无砟轨道结构层间界面力学特性，国内外学者已开展诸多试验研究。主要通过缩尺试验和实尺试验，获得界面强度或力-位移关系曲线，前者主要包括小试件拉伸和剪切试验［3］，利用数字图像相关（DIC）技术，获得试件的界面力-位移关系［4-7］；后者主要包括横向和纵向推板试验［3，8］，获得单块轨道板横向和纵向力-位移关系曲线。此外，开展考虑材料压缩变形影响的推板试验，沿轨道板纵向布置5 个位移测点，获得不同位置处界面力-位移关系曲线［9］。还研究了轨道板底拉毛、刷涂界面剂等施工工艺对界面力-位移关系的影响［10-11］。近年来，内聚力模型被广泛应用于层间界面损伤研究中，探究界面损伤机理及演变过程［4-5，12-13］，分析内聚力模型参数对界面剪切破坏的影响，提出界面损伤的修复措施［14］。

综上所述，缩尺模型试验可通过大量试件样本快速获得界面强度、刚度、断裂韧度等关键参数，试验成本较低，但试件尺寸效应明显，难以获得准确的力-位移关系，测得的参数离散性大，准确性和可靠性无法保证。实尺模型试验可在很大程度上减小尺寸效应，消除界面局部不连续、不均匀造成的试验结果偏差，且测得的参数更接近工程实际应用，但实尺模型试验很难测得界面法向力学性能参数，且对试验场地、试验设备要求高，试验成本很大，无法大量开展。目前国内外已完成的缩尺和实尺模型试验缺乏必要的理论支撑，得到的层间界面法向和切向力学性能关键参数缺乏理论依据和试验验证，将这些参数用于层间界面损伤机理及演变规律研究，能否获得可靠的、具有实际工程应用价值的结果尚未可知。在此，基于断裂力学理论中的双线性内聚力本构模型，开展CRTS Ⅱ型板式无砟轨道结构的缩尺、实尺水平推板试验，将试验获得的内聚力模型参数用于模拟仿真计算，模拟了水平推板试验全过程。最后，通过实尺试验和模拟仿真计算两者所得界面力-位移关系的对比分析，验证了推板试验原理和试验结果的可靠性，提出了层间界面合理的力-位移关系曲线和内聚力模型参数的建议取值范围，为CRTS Ⅱ型板式无砟轨道建模计算和实际工程应用提供了理论参考。

1 双线性型内聚力本构关系

基于断裂力学理论，根据层间界面的相对位移，界面损伤的主要原因有纯拉伸、纯剪切及混合加载。三维渐进损伤分析方法可准确描述法向和切向应力混合加载引起层间界面损伤的发展过程。计算中采用Quads准则判断层间界面损伤：

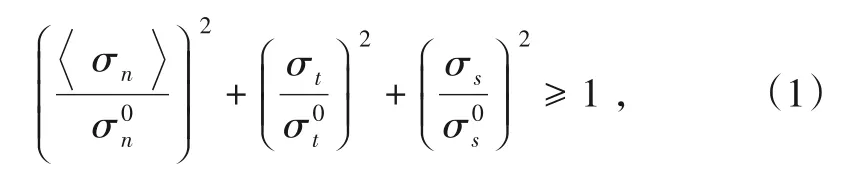
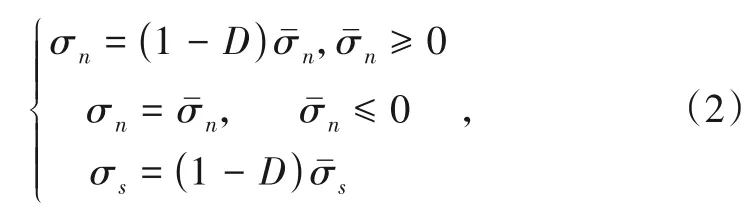
图2 层间界面损伤过程及加载路径示意图

图2中，初始加载路径的斜率为层间界面法向和切向刚度En、Es，二次加载路径的斜率为界面损伤后的法向和切向刚度(1 -D)En、(1 -D)Es。图中、分别为纯拉伸、纯剪切导致损伤发生时的法向和切向位移；为纯拉伸、纯剪切导致界面黏结失效时的法向和切向位移。GIC、GIIC为纯拉伸和纯剪切时的界面断裂韧度，量值等于三角形的面积，即或总刚度损伤为：

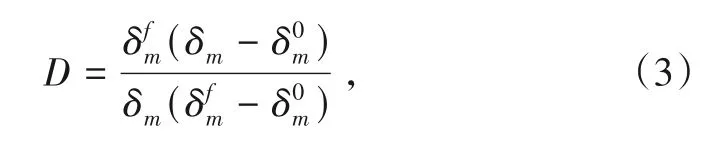
式中：当表现为纯法向损伤时，m=n；当表现为纯切向损伤时，m=s。初始加载时，力-位移关系沿“加载”应力路径不断增大，达到峰值时，层间界面发生损伤；然后，损伤不断发展，达到一定阶段时卸载，力-位移关系由“卸载”路径返回至0 点，此路径也是“二次加载”的应力路径。以此类推，每加载1 次，δm就更接近层间黏结失效的临界位移。

2 水平推板试验

2.1 缩尺试验

首先开展CRTS Ⅱ型板式无砟轨道结构水平推板缩尺试验，试验方案设计示意见图3。缩尺试验样本为5 组。每组样本从上到下依次为混凝土试件、CA 砂浆层、底座板，混凝土试件尺寸为0.60 m（长）×0.20 m（宽）×0.20 m（高）。试验阶段测试5 组样本，测试时间为CA 砂浆浇筑后28 d。开展试验时，加载位置位于混凝土试件横截面中心，2个位移计分别布置于混凝土试件左右两端。水平推板缩尺试验现场布置见图4。

图3 水平推板缩尺试验方案设计示意图

图4 水平推板缩尺试验现场布置图

缩尺试验中，有3 组样本未测得有效的力-位移关系曲线，仅得到层间黏结破坏时的最大推力FH，用FH除以黏结面积，即可求得。其余2组样本编号为C11和C14的力-位移关系曲线中，FH达到最大值时的切向位移即为界面损伤萌生时的临界位移，将力-位移关系曲线接近水平直线时的位移视为层间离缝时的临界切向位移，根据和求得Es、、GIIC。测得的水平推板缩尺试验力-位移关系曲线见图5，计算所得水平推板缩尺试验内聚力参数见表1。

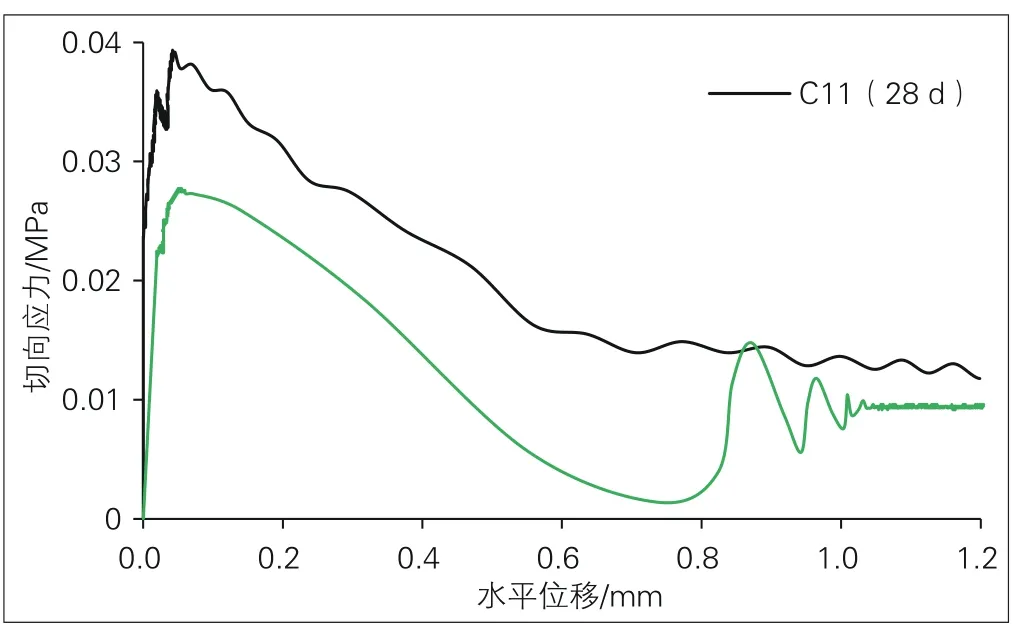
图5 水平推板缩尺试验力-位移关系曲线

表1 水平推板缩尺试验内聚力参数

2.2 实尺试验

水平推板实尺试验见图6。首先在轨道板与反力墙之间预留一定距离，以满足布置钢梁、安装千斤顶及压力传感器的需要；然后通过液压千斤顶对轨道板施加纵向水平推力，由压力传感器测得纵向水平推力，由位移传感器测得轨道板纵向位移；最后施加纵向水平推力直至轨道板与CA 砂浆层之间的层间黏结破坏，获得剪切应力-位移关系曲线。

图6 水平推板原位实尺试验

实尺试验中，3 组样本未测得有效的力-位移关系曲线，仅得到层间离缝时的最大推力FH，除以黏结面积，即可求得。由于层间离缝时FH达最大值时的位移比界面损伤萌生时的临界位移δ0s大，因此，其余2组样本无法直接得到界面法向内聚力参数Es、、GIIC，该2 组样本得到的力-位移关系曲线见图7，识别出和，即可求得，进而算得Es、GIIC，所得内聚力参数见表2。

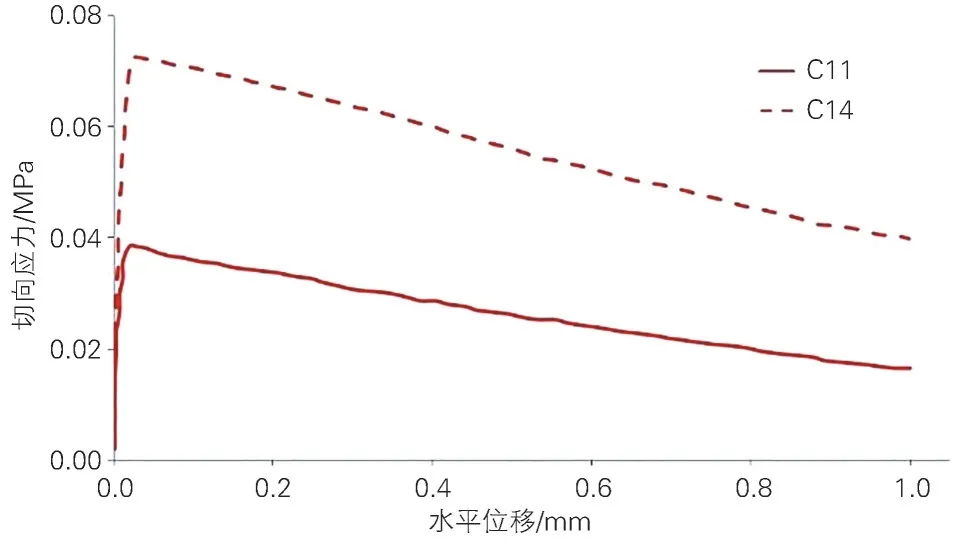
图7 单块轨道板水平推板实尺试验结果

表2 水平推板实尺试验内聚力参数

2.3 试验结果分析

（1）对比实尺试验和缩尺试验结果，可知差异不大，缩尺试验为实尺试验的2倍以上，实尺试验得到的其余内聚力参数均大于缩尺试验结果，其中，Es约为缩尺试验的2~3倍，约为缩尺试验的2倍，GIIC约为缩尺试验的2~7倍。对比分析可知，实尺试验和缩尺试验结果存在差异，但差异的倍数关系基本一致，根据模型试验的相似准则，缩尺试验结果具有一定的合理性和可靠性。由于开展原位实尺试验成本太高，实验过程复杂，结果可控性差，因此，可开展缩尺试验获取层间界面内聚力参数。

（2）国内外同类研究给出的不同尺寸试验切向内聚力参数拟合结果汇总见表3。从表中可以看出，缩尺试验的最大切向应力可达1.000 0 MPa，约为实尺试验的25 倍；损伤萌生的位移为0.015 0 mm，约为实尺试验的1/3；缩尺试验测得的切向刚度可达实尺试验的70 倍，约为70 000 MPa/m。对于断裂能，缩尺试验与实尺试验相差较小，为10.0～70.0 J/m2。京沪高速铁路股份有限公司（简称京沪公司）推板试验得到的界面刚度较大，最大的切向应力为0.036 5～0.073 0 MPa，为其他组试验值的3～6 倍；而损伤萌生的位移为0.025 0～0.050 0 mm，较其他试验值小。德国马克斯·博格公司（简称博格公司）的层间界面切向刚度为30 MPa/m，约为京沪公司的1/50；最大切向应力为0.024 0 MPa，与京沪公司的差异较小；损伤萌生的位移为0.800 0 mm，为京沪公司的16 倍；CA 砂浆界面可延展至3.000 mm，是京沪公司的1.5 倍。可以看出，相比于京沪公司采用的CA 砂浆，博格公司CA 砂浆的切向性能在损伤萌生位移和离缝萌生位移均表现出一定优势。根据表3 中的推板试验实测数据，给出我国CRTS Ⅱ型板式无砟轨道层间界面的切向界面刚度建议值，为500 ～1 500 MPa/m；切向强度建议取值0.02 ～0.07 MPa；切向断裂韧度建议取值10.0 ～30.0 J/m2。

表3 不同尺寸试验切向内聚力参数拟合结果汇总

3 水平推板试验数值仿真

3.1 建立模型

为验证水平推板试验获得的力-位移关系和内聚力参数，建立CRTS Ⅱ型板式无砟轨道结构三维渐进损伤分析模型，对水平推板实尺试验的层间界面损伤过程进行模拟。水平推板试验全过程反演分析模型见图8，模型主要由轨道板、CA 砂浆层和底座板组成。轨道板长6.45 m，宽2.55 m，底座板宽3.25 m。各层厚度见图8中剖面图。建模时，轨道板、CA 砂浆层及底座板均采用C3D8R 单元模拟，轨道板与CA 砂浆层、CA 砂浆层与底座板之间的层间界面均采用内聚力单元COH3D8模拟。

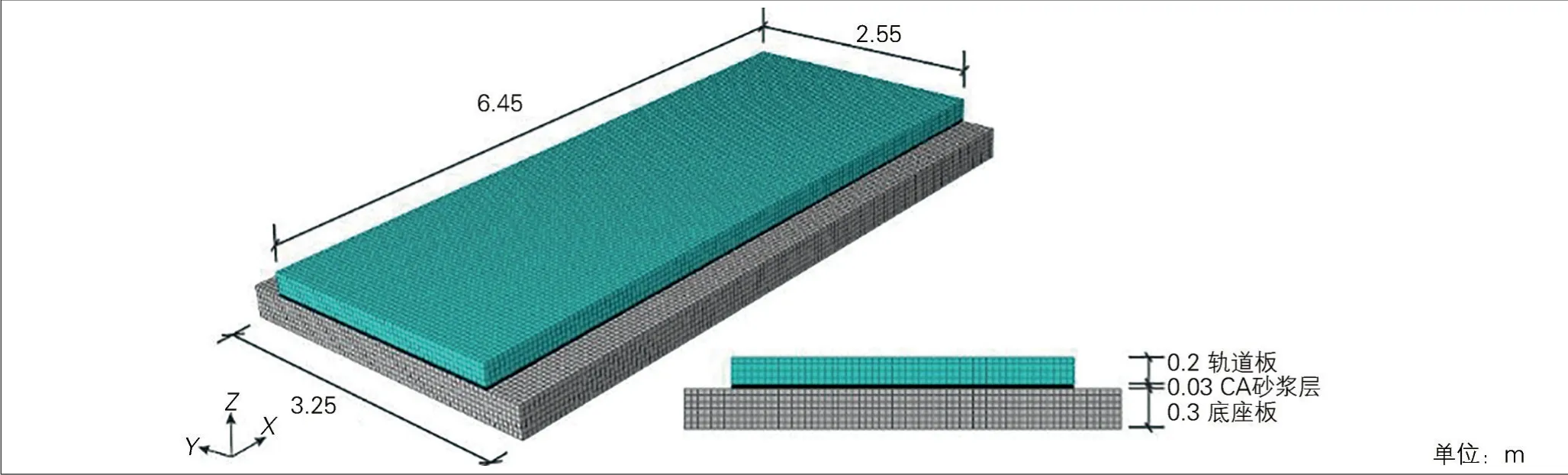
图8 水平推板试验全过程反演分析模型

3.2 数值仿真

轨道板、CA 砂浆层和底座板的弹性模量分别为3.60×104、1.00×104MPa 和2.20×104MPa，密度分别为2 500、1 950 kg/m3和2 400 kg/m3。加载时沿轨道板纵向逐级施加1 mm 位移荷载。层间界面初始状态均为完全黏结，即界面无损伤，底座板底面节点全约束。在水平推力作用下，轨道板纵向位移从0 mm 增至1 mm时，界面纵向剪应力沿轨道板纵向分布规律见图9，总刚度损伤沿轨道板纵向变化规律见图10。

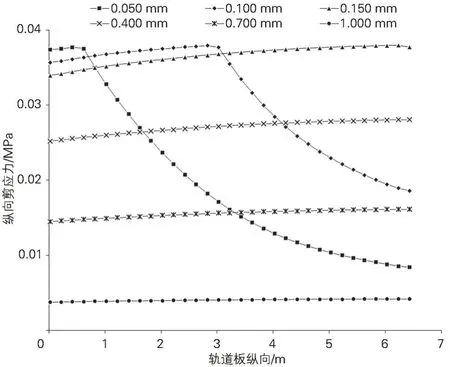
图9 界面纵向剪应力沿轨道板纵向分布规律

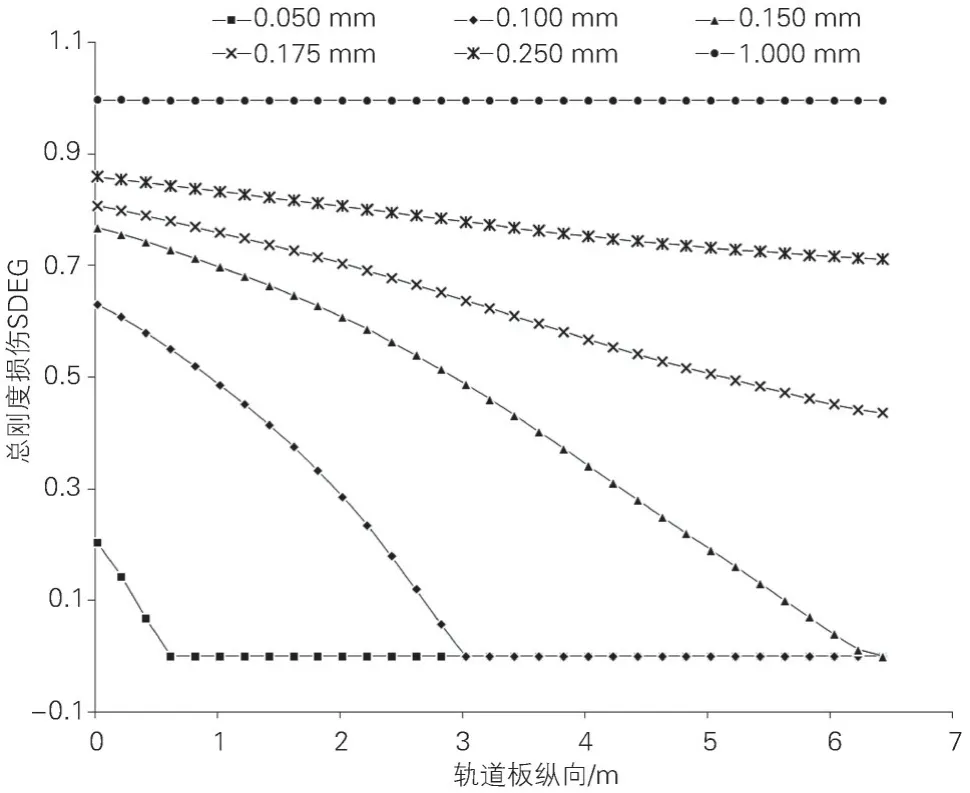
图10 总刚度损伤沿轨道板纵向变化规律

3.2.1 轨道结构层间界面剪应力变化过程

由图9 和图10 可知，轨道结构层间界面剪应力变化过程主要分4个阶段：

（1）轨道板纵向位移为0.05 mm 时，受荷近端0~0.62 m 剪应力达到最大值0.037 0 MPa，该范围总刚度损伤很小，由0.2 降至0.0，即层间界面的大部分区域尚未发生损伤。剪应力沿纵向传递至受荷远端，在0.60 ~6.45 m 逐渐呈非线性降低，远端剪应力为0.008 0MPa。

（2）轨道板纵向位移为0.05 ~0.15 mm 时，最大剪应力约为0.037 0 MPa，层间界面开始损伤且逐渐发展至整个界面。

（3）轨道板纵向位移为0.15 ~1.00 mm 时，层间界面剪应力逐渐降低，层间界面损伤区域随轨道板纵向位移增大而逐渐增加。

（4）当轨道板纵向位移大于1.00 mm时，剪应力降低至0.004 0 MPa，层间黏结失效。

3.2.2 纵向水平推板试验过程

分析可知，纵向水平推板试验过程可分为3 个阶段：

（1）无损伤阶段。层间界面剪应力非均匀分布，且沿受荷近端至远端逐渐降低。

（2）部分损伤阶段。随纵向位移不断增加，层间界面剪应力逐渐趋于均匀分布，当整个界面受最大剪应力均匀作用时，层间界面损伤萌生。

（3）完全损伤阶段。随均匀分布的界面剪应力不断下降，损伤不断发展，直至层间离缝。

将水平推板实尺试验和仿真结果进行对比（见图11）。可知，仿真结果和试验结果吻合度较高，在无损伤阶段，均呈明显线性；在出现损伤后，仿真结果和试验结果差异逐渐减小。

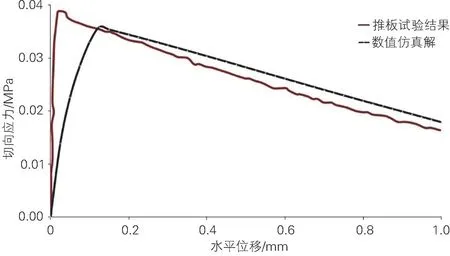
图11 水平推板实尺试验和仿真结果对比

3.3 仿真结果分析

分析不同界面切向刚度和断裂韧度时，界面剪应力和轨道板纵向无损伤区段长度的关系；分析不同界面切向刚度的影响时，切向强度固定取值为0.04 MPa，断裂韧度为21.0 J/ m2，界面刚度分别为30、100、1 000、5 000 MPa/m；分析不同断裂韧度的影响时，切向强度固定取值为0.04 MPa，切向刚度为1 000 MPa/m，断裂韧度分别为5.0、10.0、20.0、40.0 J/m2。

界面切向刚度对无损伤区范围的影响见图12，断裂韧度对损伤区范围的影响见图13。根据图12，不同界面切向刚度对应的无损伤区段等效长度分别约为40.0、30.0、12.0、6.5 m；无损伤区段长度随着界面切向刚度增大而逐渐越小；当界面切向刚度为30 MPa/m时，无损伤区段长度约为6块轨道板长度，是界面切向刚度为1 000 MPa/m 时的5.6 倍。根据图13，损伤区段长度随断裂韧度增大而逐渐增加。可以认为，界面切向刚度越大，界面应力不均匀性越明显；随着断裂韧度的增大，损伤区段长度不断增加。

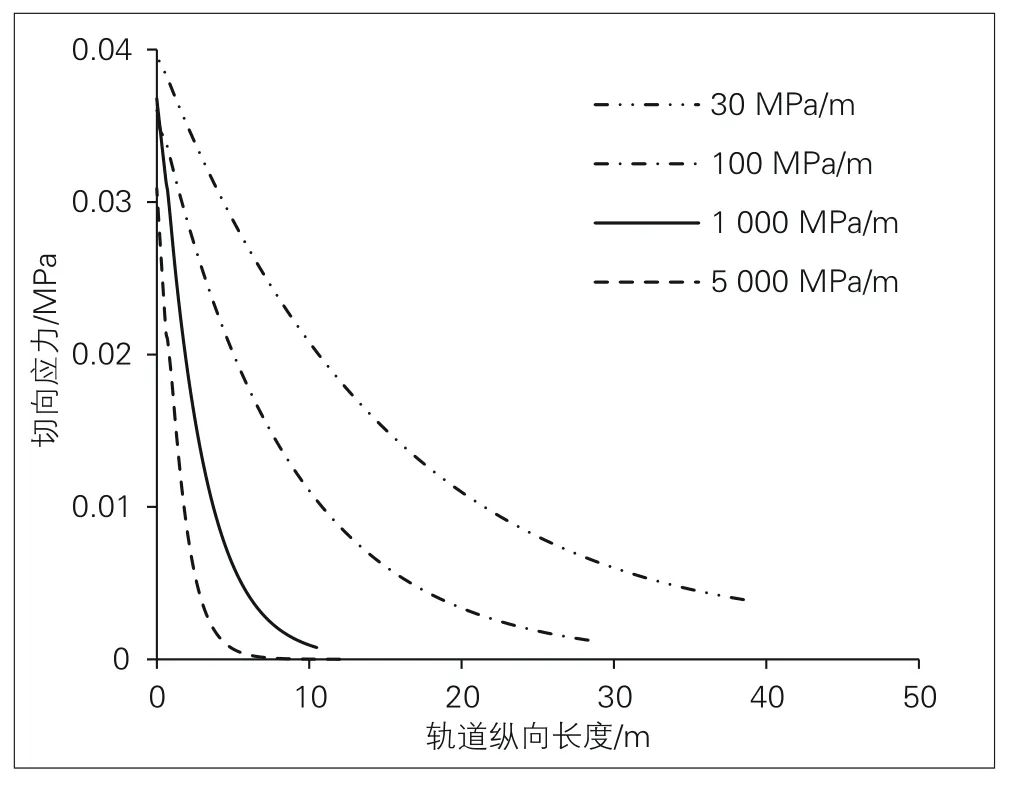
图12 界面切向刚度对无损伤区范围的影响

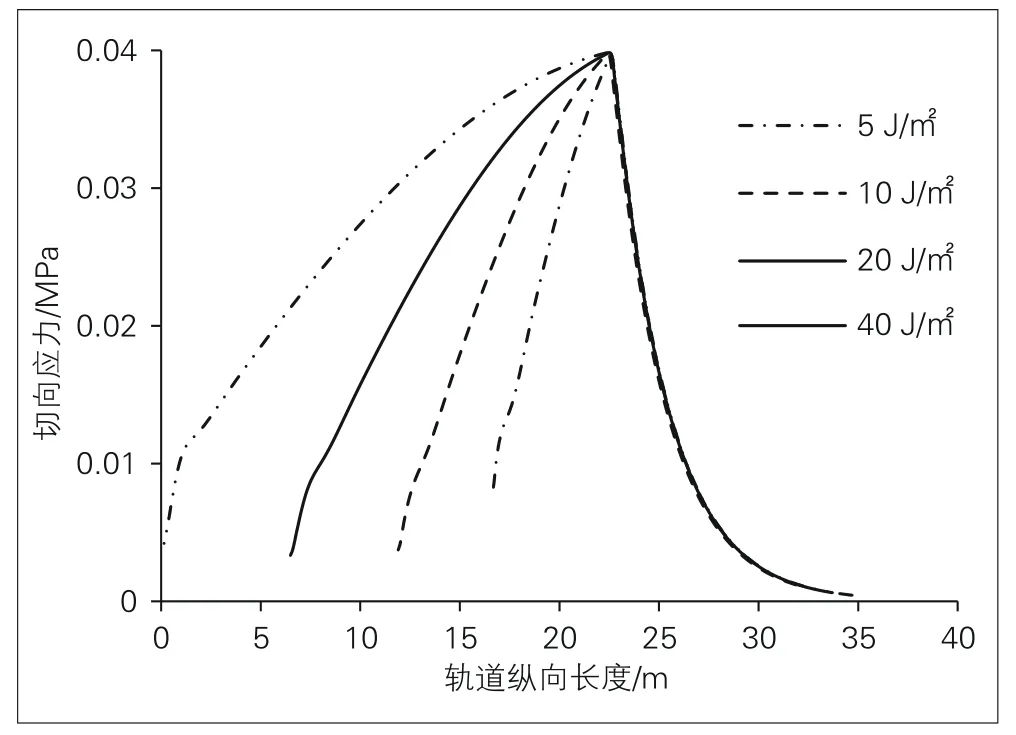
图13 断裂韧度对损伤区范围的影响

4 结论

基于水平推板缩尺、实尺试验，获得了CRTS Ⅱ型板式无砟轨道层间界面切向力-位移本构关系，得到切向内聚力参数。并借助数值仿真，对水平推板实尺试验全过程进行模拟，得到以下结论：

（1）开展水平推板缩尺、实尺试验，得到了层间界面切向力-位移关系曲线。通过试验获得的力-位移关系曲线，可得到层间损伤萌生和层间黏结破坏时的临界位移，进而得到界面强度、界面刚度和断裂韧度。

（2）实尺试验可在很大程度上减小试验样本的施工质量、结构尺寸、加载条件等因素对试验结果的影响，故能获得较好的试验结果，但成本太高不宜大量开展。缩尺试验样本成本较低，可大量开展，获得内聚力模型参数范围，但试验结果合理性需进一步验证。高速铁路实际工程中，通常采用实尺和缩尺试验结果的对比验证，来获得模拟仿真计算中内聚力参数的最优取值。

（3）界面切向刚度越大，层间变形协调能力越弱，界面损伤的非均匀性越显著，越容易出现应力集中；断裂韧度越大，轨道板越不容易出现离缝。

（4）通过仿真和试验结果对比分析，得到内聚力模型参数的合理取值：界面切向刚度800～1 000 MPa/m，切向强度0.03～0.04 MPa，切向断裂韧度10.0～20.0 J/m2。