结合常微分方程的压缩视频质量提升算法

王 越 何小海 吴晓红 任 超

（四川大学 电子信息学院，四川 成都 610065）

由于网络存储和传输能力有限，通常需要将待传输视频进行压缩来缓解压力。但压缩会对原始视频的质量造成一定的损失。如何让压缩后的视频恢复一定的高频细节，减少部分人工痕迹，需要进一步的深入研究。

针对消除压缩带来的伪影这一问题，近年来已经有许多团队提出了优异的算法。在文献[2]和[3]中，均对当前问题设计出一种滤波器，来改善压缩视频帧的阻塞和振铃效应。为了提高伪影减少的性能，稀疏编码技术也被广泛使用。譬如，Chang 等人[4]参考稀疏编码，通过学习强大的表示法来减少压缩伪影。Tang 等人[5]提出了一种自适应HEVC 压缩视频去块方法，对压缩视频进行预处理、奇异值去除和滤波操作，显著提高了视频质量。Yang等人[6]首次提出了多帧质量增强（MFQE 1.0）方法，以有效利用相邻帧的时间信息。Yang 等人在MFQE 1.0 的基础上又提出了MFQE 2.0[7]，以进一步提高MF-CNN 的效率，并实现了较先进的性能。STDF[8]引入了一种时空可变形融合方案用于去压缩任务，以捕获最相关的上下时空特征信息，排除噪声内容，从而提高目标帧的质量。

为求增强压缩视频质量，本文提出一种结合常微分方程的视频去压缩方法。该方法利用神经网络中残差结构与常微分方程求的解公式有相似的表示形式，将常微分方程（ODE）引入网络，以增强网络捕获重要特征信息的能力，促进高频细节信息的恢复。具体内容将会在下一章进详细说明。

1 结合常微分方程的视频质量提升方法

1.1 基于常微分方程（ODE）的网络结构

本节将从动力系统的角度，将常微分方程（ODE）的理论知识应用到网络模块结构的设计中。数学上，常微分方程的定义如下：

其中p 和z 分别表示自变量和因变量，f(p,z)也可以用z'来表达当前的求导操作。网络中的映射关系可以使用ODE 如下表示：

其中，Φ 表示映射关系，z0代表网络的输入特征。

对于给定初值的常微分方程（即初值问题），通常会通过前向欧拉算法进行求解，由于当前网络更接近于非线性，前向欧拉算法的表达形式如下：

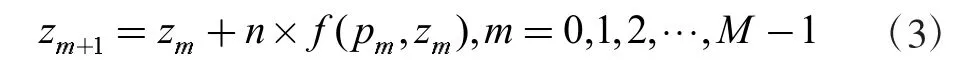
在这里，n 表示步长，pm=m×n(m= 0,1,2, …,M)代表一段区间 [0,T（]M 等份）中的节点。

在神经网络中，残差结构的通用表达式如下：

其中，R(·)表示残差操作。可以直观的看出，式（3）和式（4）间具有一定的相似性，所以，这里将式（4）用式（3）代替。需要注意的是，式（3）即前向欧拉算法是常微分方程求解中的一种较简单的方法，往往缺乏稳定性和精确度。因此，这里将前向欧拉算法替换为二阶Velocity-Verlet 算法，重新书写求解表达式如下：

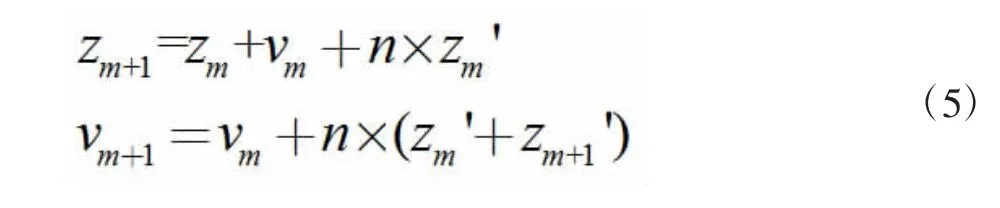
其中，vm和vm+1代表的是动力系统中的速度。为求将常微分方程有效引入网络模块中，将速度用经过卷积后的某一特征代替；另外，在网络中将式（5）里求导操作用一个3×3 卷积表示；n 经验性地设为0.5。最终设计出的基于ODE 的网络模块如图1 所示。

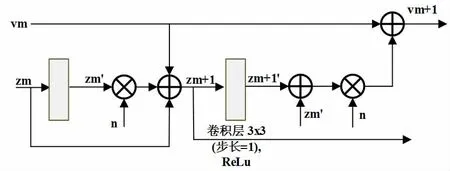
图1 基于ODE 的网络模块

1.2 结合常微分方程的压缩质量提升网络

如图2 所示，本文提出方法的网络结构大致分成三个步骤：

图2 结合常微分方程的压缩视频后处理整体网络框图

1.2.1 特征提取：在该步骤中，本文提出的方法采用了U-net 的形式，旨在获取输入的特征谱中的有用信息，同时能够增大一定程度的感受野，进一步促进时间动态的捕获。U-net 结构中的下采样和上采样分别通过步长为2 的卷积操作和反卷积操作来完成。除此之外，在经典的U-net 网络结构上，还增加了额外的两个跳连接和concatenate，以此进一步增强网络捕获特征信息的性能。另外，在U-net 网络结构中的所有激活函数都使用的是ReLU 函数。

1.2.2 时空可变形融合：为了更好地去探索时间信息，本文参考文献[8]使用了一种时空可变形融合模块，以提高相邻帧之间的时空信息的利用率，促进光流的估计。本文以目标帧及其相邻参考帧作为输入，共同预测偏移场以使卷积的时空采样位置变形，来自目标帧和参考帧的互补信息可以在单个时空可变形卷积操作中融合[11]。

1.2.3 质量增强：在质量增强步骤中，本文将1.1 节介绍的基于常微分方程的网络结构经验性地以每三个一组、一共十二个的组合方式，放入网络中；为了进一步提炼特征信息，提高去压缩性能，在每一组模块后，增加了两层卷积，最终的基于常微分方程的网络结构如图2 所示。

2 实验结果展示与分析

2.1 实验配置

本文使用公开数据集中108 个视频作为网络的训练数据集。测试视频序列采用了五种不同分辨率大小的18个未压缩视频，并且使用HEVC[1]压缩标准，在HM-16.0上采用帧间（LDP）模式对视频进行压缩。选择的四种质量因子（QP）分别为27，32，37 和42。

在输入序列的帧数选择中，本节参考文献[8]，经验性地将每7 帧连续的压缩视频帧作为一组训练数据输入到网络中。为了加快收敛速度，网络训练采用ADAM[12]优化方法。本节采用增量峰值信噪比（ΔPSNR）和增量结构相似性（ΔSSIM）[13]来评估质量增强性能，即本节给出的不同算法客观参数对比，是每一种算法在测试视频里得出的客观参数，与当前测试视频经HEVC 压缩后得出的差值。

2.2 不同压缩视频后处理方法对比

本节将提出的压缩视频后处理方法与当前主流的图像/视频质量增强方法进行了比较。表1 给出了不同后处理方法在测试集上计算出的PSNR 和SSIM 与HEVC 压缩后的视频帧的差值ΔPSNR 和ΔSSIM。可以明显地观察到，本文提出的方法在18 个测试视频的平均ΔPSNR 和ΔSSIM 方面始终优于所有对比方法。这说明本文所提出的压缩视频后处理方法能够更加显著的提高压缩视频的质量。本文提出的方法在ΔSSIM 和其他QP 与其他方法相比也有类似的结果。值得注意的是，本文方法的参数量较小，同样具有一定的优势。

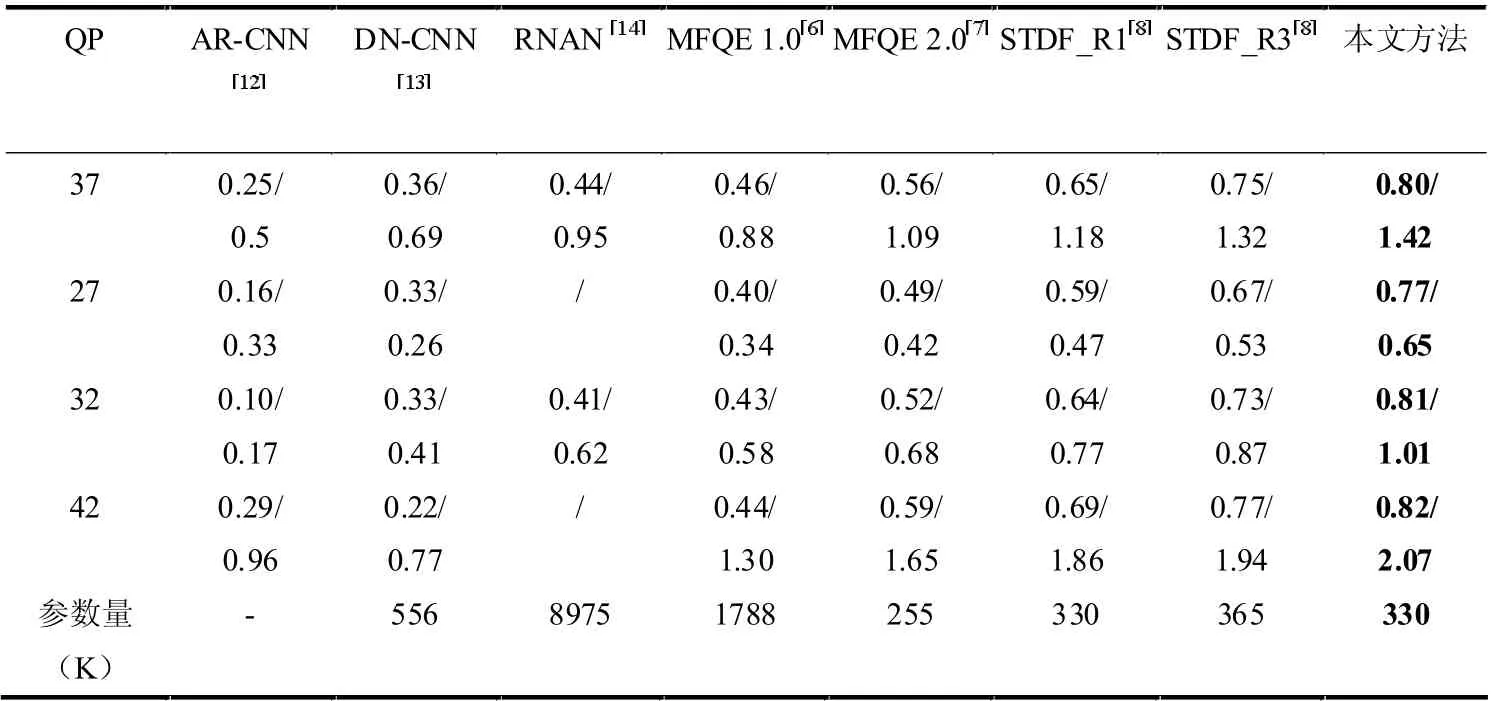
表1 不同压缩视频后处理方法客观参数对比（ΔPSNR（dB）/ΔSSIM（10-2））

图3 展示了在QP=37时不同方法的主观视觉效果对比。从图3 中可以直观的看出，本文方法重建视频帧中包含有更加丰富的细节，边缘也较锐利，更为接近原始视频帧。而经其他方法增强后的视频帧还存在着一定程度的压缩效应。因此，本文提出的方法能够更好地提升压缩视频帧的质量。

图3

2.3 基于常微分方程网络模块的有效性验证

本节将通过消融实验来验证所提出基于ODE 的网络模块的必要性。在本节中，将网络中质量增强部分的所有常微分方程块替换为普通的卷积块，用此网络结构重新训练，与本文原方法在QP=42 时结果的客观参数对比如表2 所示。从表中可以非常直观的看出，使用基于ODE 网络模块的网络所得出的客观参数结果更高，说明本文提出的结合ODE 的网络模块能有效提高去压缩性能。

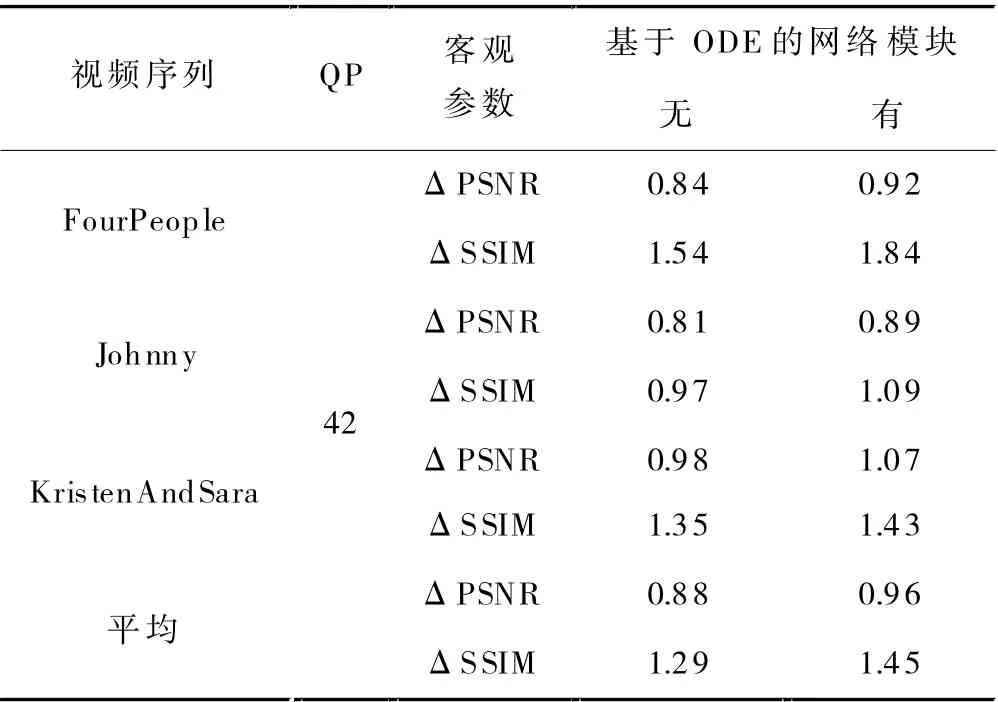
表2 常微分方程块对网络结果的影响

图3 不同方法在Johnny（2560×1080）上的主观视觉效果对比图（a）原始视频帧（PSNR/SSIM）；（b）HEVC 压缩图像（36.62/0.9315）；（c）MFQE2.0[9]（36.94/0.9342）；（d）STDF_R1[10]（37.01/0.9348）；（e）STDF_R3[10]（37.06/0.9352）；（f）本文方法（37.29/0.9370）。

3 结论

为了有效改善HEVC 压缩带来的人工痕迹，本文在参考常微分方程后，利用卷积神经网络的残差块在数学表达式上与常微分方程的求解公式有着类似的表达，将常微分方程引入压缩视频质量提升网络中，设计出一种结合常微分方程的网络模块，以提高去压缩性能。大量实验结果表明，和对比方法相比，经本文提出的方法生成的视频细节信息较为丰富，主客观质量良好。