中美股票市场风险传染效应分析——基于相关性结构分解

郑延婷， 栾 昕， 黄 凤

(1.北京工商大学， 北京 100048； 2.中信期货北京分公司， 北京 100010)

资本市场风险传染是学界及业界关注的重点问题。在国际市场中，美国股票市场凭借其强大的全球影响力，一直居于核心位置。自2013年以来，中国股票市场的区域影响力日益提高，与国际主要股票市场的关联性逐渐增强，开始进入全球投资者和监管机构的视野[1-3]，对中美股市之间风险传染效应的研究也变得至关重要。相关性分析是研究风险传染效应的基础，中美股市的相关性经历了从无到有，从简单到复杂的演变过程，逐渐呈现非线性、非对称性等复杂特征。2005年之前，中美股市行情各自独立，几乎不存在相互影响；随着中国股票国际化进程的加快，美股收益率对中国A股呈现显著的单向溢出，极端情形下两市还会表现出非对称的双向波动性溢出。2019年，A股接连被纳入MSCI、富时罗素和标普道琼斯三大国际指数，点燃了大型机构投资者关注中国市场的热情，同时也意味着中国A股市场与全球股市相关性将进一步加强。2020年，新冠肺炎疫情及沙特发起的石油价格战两大“黑天鹅”事件引发美股市场剧烈震荡，深度牵连中国A股市场。那么，中美股市之间相关性增强是否意味着风险传染的发生？如果存在风险传染效应，传染的方向如何？洞悉两国的风险传染效应，将有助于我国应对国际金融市场的冲击，制定有针对性的风险管理策略。本文以中美股市之间风险传染效应为主要研究对象，对以上两个问题进行了科学回答。

本文的主要贡献体现在：第一，借助联合概率空间划分方法将市场行情因素融入中美股市风险传染效应的分析中，采用Zheng et al.[4]提出的分块混合Copula模型，在不同市场行情下实现中美股市间相关性结构的分解，区分传染、分散及独立风险效应，并重点关注极端市场行情下中美股市间的风险传染效应，深层次理解两国股市之间的风险传染机理。第二，借鉴Bradley & Taqqu[5]空间传染的定义，本文给出一类新的风险传染效应度量以及传染方向识别的方法，利用不同市场行情下分解系数的差异来研究中美股市风险传染效应，拓展了风险传染效应的研究视角。

一、文献综述

针对跨市场金融风险传染的研究已形成了大量有价值的文献。多数学者从收益率均值、波动性或极端风险等层面，研究跨市场间的风险溢出效应。常用的方法有格兰杰因果检验、VAR、GARCH模型[6-8]以及Diebold & Yilmaz[9]提出的广义预测误差方差分解模型等。另有一些文献直接从相关性角度出发，并发现相关性在风险传染过程中表现出非线性和非对称的特征[10-13]。虽然学界对相关性增强是否导致风险传染观点各异[14-15]，但是风险传染以相关性的存在为前提条件已逐渐成为普遍共识。

当前，中国已成为世界第二大经济体，中美两国之间的博弈逐渐成为世界关注的焦点。随着中美股市之间相关性的增强，两国金融市场之间的风险传染[16-18]也逐渐成为研究热点。但是针对中美股市间相关性的内在结构进行研究，以此来分析两国市场间风险传染效应的文献仍然较少。董秀良、曹凤岐[19]运用多元GARCH模型实证得到，美国股市对中国股市波动溢出效应不显著，风险传染总体处于较低水平。吴吉林、张二华[20]运用动态Copula方法研究了2005—2009年中美股市的相依性结构，发现次贷危机期间中美股市间的相关性反而下降，并未表现出风险传染。许多实证研究与上述观点持不同看法。李岸等[21]构建MGARCH-BEK模型研究发现，在中国金融自由化进程中，中美两国股市存在显著的双向波动溢出效应。与此同时，王治政、吴卫星[22]运用ARCH模型研究发现，美国股票市场对中国股票市场存在较为显著的单向溢出效应。由此可见，不同学者得到的结论存在差异甚至完全相悖。

现有文献对于中美股市风险传染效应的研究也较多集中在风险溢出角度，对中美股市基础相关性结构的重视略有不足。事实上，相关性的内涵要大于风险传染。相关性不仅包括正相关，还包括独立和负相关，正相关性提升会加剧风险溢出，引发风险传染；而独立和负相关性会带来一定程度的风险分散效果，反而会对风险传染起到对冲或屏障作用。危机进程中，风险分散效应与传染效应存在转换关系。例如，Baur & Lucey[23]认为，在市场危机的初期，投资者总是追求更高质量的资产(flight to quality)，这种交易行为使得市场之间相关性减弱，产生了风险分散效应。此外，无论相关性还是风险传染效应，其表现都因市场行情的不同而存在差异。因此，学者们往往重点分析极端市场行情下的风险传染效应，这具有一定的合理性[24-27]。然而，对行情切换过程中，市场之间风险传染效应的研究尚待深入探索。

综上所述，本文拟采用分块混合Copula模型，在不同市场行情下，运用Frechet型混合Copula模型分解中美股市之间相关性的内在结构，并通过检验不同市场行情下分解系数差异的显著性来研究风险传染效应。具体来说，在不同市场行情下，将中美股市之间的相关性解构出传染、分散及独立三种代表性效应，传染效应是指一方收益率上涨或下跌时，另一方收益率同向变动；分散效应是指一方收益率上涨或下降时，另一方收益率反向变动；独立效应则指一方收益率上涨或下降时，另一方收益率独立变动。

二、模型设计

假设R1和R2分别表示中国和美国股票指数的日对数收益率，其边缘分布函数分别为F(·)和G(·)，其联合分布函数为H(·,·)。本文采用Copula函数捕捉两市之间的相关性特征，进而分析两市之间的风险传染效应。根据Sklar定理，对于上述联合分布函数H(·,·)，存在Copula函数C(·,·)，使得下式成立：

H(x,y)=C(F(x),G(y)),∀x,y∈(-∞,+∞)

(1)

如果边缘分布函数F(·)和G(·)均为连续函数，则式(1)中的Copula函数唯一存在。通过概率积分变换令U=F(R1)，V=G(R2)，那么U和V均服从[0,1]区间上的均匀分布，经过简单计算可知，(U,V)的联合分布函数即为式(1)中的Copula函数C。不难发现，运用Copula模型进行相关性研究有两个关键步骤：一是单个变量的边缘分布拟合；二是在概率积分变换基础上进行Copula函数拟合。下文将按照以上两个关键步骤进行模型设计。

(一)边缘分布拟合

由于金融时间序列多呈现波动聚集、尖峰厚尾等特征，实证研究多选用GARCH模型进行边缘分布拟合。除此之外，非参数经验模型也是一类处理尖峰厚尾特征的重要方法，相比参数化的模型方法，在数据充足的情况下，经验模型能够最大限度地避免设定风险，实现较高的边缘分布拟合精度，本文采用的分块混合Copula模型就属于半参数模型。具体而言，对于金融时间序列{Rt}t=1,2,…,n，其未光滑化的经验分布函数为：

(2)

(3)

边缘分布函数拟合后，式(2)和式(3)中经验分布函数的不连续性会导致边缘分布概率积分转换不稳健，因此本文采用cubic三次样条插值法对其进行光滑处理，以增加边缘分布概率积分转换的稳健性。

(二)相关性拟合及分解

在金融市场中，低迷、繁荣以及正常三种行情往往交替出现，而市场之间相关性在这三种行情中的表现并不一致，因此市场行情是相关性研究中不可忽略的因素。本文采用概率方法对低迷、繁荣以及正常三种市场行情进行划分，研究不同市场行情下中美股市之间的相关性结构。

1.市场行情的概率划分

相比正常行情时，相关性在极端行情(包括低迷和繁荣两种行情)中会显著增大，并且低迷行情的增幅通常会高于繁荣行情，体现出非对称性。按照Bradley & Taqqu[5]的观点，如果市场R1出现危机事件，两市场的相关性显著高于R1处于正常状态时的相关性，那么市场R1对市场R2存在传染效应。本文借鉴Bradley & Taqqu[5]对风险传染的定义，根据金融变量R1和R2的分位数函数以及Copula函数，对市场行情进行概率空间划分。具体来说，记Q1(·)和Q2(·)分别为中美股票指数的对数收益率R1和R2的分位数函数，则对任意q∈[0,1]，有：

Q1(q)=inf{R1|F(R1)≥q}

(4)

Q2(q)=inf{R2|G(R2)≥q}

(5)

结合Copula函数定义有：

C(q,q)=P(R1≤Q1(q),R2≤Q2(q))

(6)

本文将两国股指收益率均处于下尾部区域[-∞，Q1(q)]×[-∞,Q2(q)]时，定义为低迷行情；将二者收益率均处于上尾部区域[Q1(1-q),+∞]×[Q2(1-q),+∞]时，定义为繁荣行情；将二者收益率均处于区域[Q1(q),Q1(1-q)]×[Q2(q),Q2(1-q)]时，定义为正常行情。在相对应的Copula概率空间中，区域[0,q]×[0,q]代表低迷行情空间，区域[1-q,1]×[1-q,1]代表繁荣行情空间，区域[q,1-q]×[q,1-q]代表正常行情空间。为了方便说明和测算，本文采用分位数等分法，即选取q=1/3，并在图1中演示了本文市场行情概率划分过程。

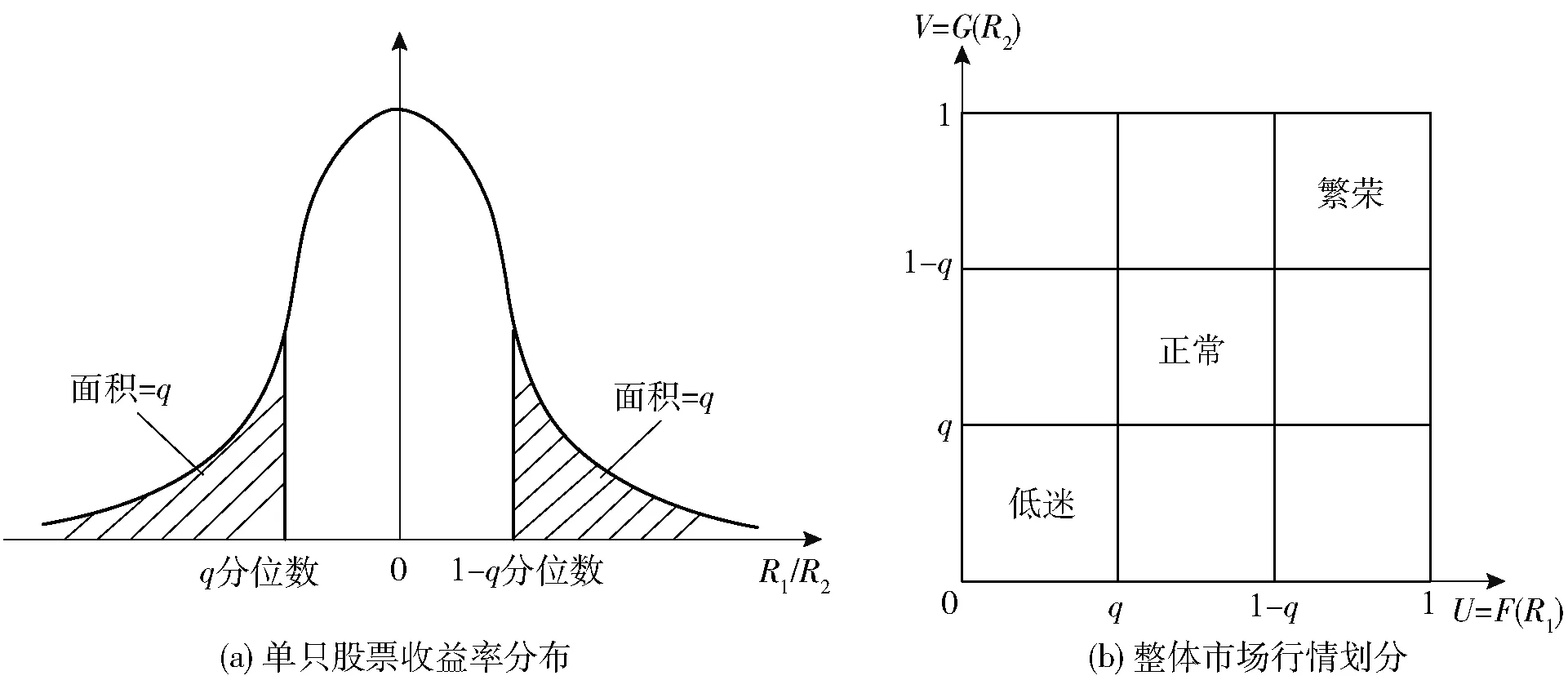
图1 市场行情概率划分图示

{Ai,j(i,j=1,2,3)}是概率空间上的一个分割，A1,1代表低迷市场行情，P(A1,1)=P(U≤1/3,V≤1/3)；A2,2代表正常市场行情，P(A2,2)=P(1/3≤U≤2/3,1/3≤V≤2/3)；A3,3代表繁荣市场行情，P(A3,3)=P(2/3≤U≤1,2/3≤V≤1)。在此特别说明两点：第一，概率空间的均匀划分并不是区分市场行情最有效的方法，本文仅为了直观地分解风险效应而做了此种简化处理，后续研究中还将进一步开展市场行情划分的方法测算与对比分析。第二，由于本文重点关注风险管理而非对冲策略，因此只关注两处正相关极端行情。在众多研究风险管理的文献中，普遍也将两收益率序列同时进入上尾或下尾区域的情况认定为极端市场条件。

2.分块混合Copula模型

在市场行情概率划分的基础上，对任意给定的Copula函数，根据全概率公式将其表示为如下分解形式：

(7)

其中，Ai,j(i,j=1,2,3)即为前述市场行情划分下所形成的概率子空间，每个子空间上的条件边缘分布记为：

Fi,j(u)=P(F(R1)≤u|Ai,j)

(8)

Gi,j(v)=P(G(R2)≤v|Ai,j)

(9)

那么，在任意市场行情Ai,j下，再次应用Sklar定理，则存在Copula函数Ci,j，使得：

P(F(R1)≤u,G(R2)≤v|Ai,j)=
Ci,j(Fi,j(u),Gi,j(v))

(10)

至此，在原始经验数据的基础上可以得到不同市场行情下的相关性函数表达式：

(11)

通过观察不难发现，式(11)中的条件Copula函数Ci,j可以具备任意复杂的函数形式，因而不利于相关性的内在结构分析。在市场行情概率划分的基础上，本文借鉴Zheng et al.[4]的做法，在每一个局部行情下构造Copula的线性凸混合逼近。在局部混合Copula函数选择时，本文并未采用带有局部相关性特征的Copula函数进行混合。原因有如下两点：第一，相比现有的分块Copula模型，进行局部混合后的分块Copula具有更好的拟合精度；第二，在金融风险管理研究领域里，大多数文献已经将研究重点放在尾部相关性度量上，常常采用具有上尾特征的Gumbel Copula、具有下尾特征的Clayton Copula、对称尾部特征的Frank Copula等进行混合。然而，在局部市场行情下，上述局部特征明显的Copula函数可能较难发挥作用，在市场行情划分的基础上，选用简易直观的基础Copula进行局部混合效果更佳。从实践角度上看，分块混合Copula模型能够将市场行情划分与相关性结构分解相结合。在众多刻画相关性结构的Copula族中，有三类相关性结构最为特殊，分别是同单调相关结构、反单调相关结构和独立结构。只是通常情况下，当人们针对金融数据进行建模时，会发现同(反)单调相关性并不常见甚至是不存在的，因而其在金融尤其是风险传染领域的应用较少。然而，随着近十几年金融危机的频繁发生，尤其是2008年金融危机时，人们发现，一些正常状态下只存在某种程度相关性的投资组合会随着危机进程加深而变得越来越同单调，尤其是规模较大的资产组合。导致该现象的主要原因是当一些隐含的系统风险积聚增大时，大多数资产未来的风险损失变大，相关性结构容易演变为同单调相关，进一步加剧风险传播而发生传染。所谓R1和R2同单调相关是指两变量受到共同风险因子U的影响，协同变动方向相同，即满足以下关系式：

P(R1≤x,R2≤y)=P(F-1(U)≤x,G-1(U)≤y)

(12)

相应的Copula函数为同单调Copula，记为M。根据Sklar定理，经过简单推导：

P(R1≤x,R2≤y)=P(U≤F(x),U≤G(y))=
min(F(x),G(y))=M(F(x),G(y))

(13)

便可以得到同单调Copula函数M(u,v)=min(u,v)。

所谓R1和R2反单调相关是指两变量受到共同风险因子U的影响，但协同变动方向相反，即满足以下关系式：

P(R1≤x,R2≤y)=
P(F-1(U)≤x,G-1(1-U)≤y)

(14)

相应的Copula函数为反单调Copula，记为W。根据Sklar定理，经过简单推导：

P(R1≤x,R2≤y)=
P(U≤F(x),1-U≤G(y))=
max(F(x)+G(y)-1,0)=W(F(x),G(y))

(15)

便可以得到反单调Copula函数W(u,v)=max(u+v-1,0)。

所谓R1和R2独立是指影响其变动的风险因子U和V相互独立，无协同变动，即满足以下关系式：

P(R1≤x,R2≤y)=P(F-1(U)≤x,G-1(V)≤y)

(16)

相应的Copula函数为独立Copula，记为Π。根据Sklar定理，经过简单推导：

P(R1≤x,R2≤y)=
P(U≤F(x),V≤G(y))=F(x)G(y)=
Π(F(x),G(y))

(17)

便可得到独立Copula函数Π(u,v)=uv。

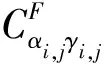
(18)

其中，混合Copula函数表达式为：

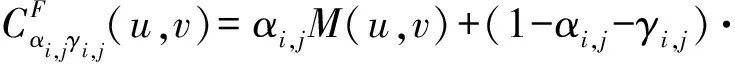
(19)

αi,j表示同单调相关结构的敏感系数；γi,j表示反单调相关结构的敏感系数；βi,j=1-αi,j-γi,j表示独立结构的敏感系数。

对比式(11)和式(18)，可以看出，任意市场行情发生的概率P(Ai,j)保持不变，股票收益率在各个市场行情下的边缘分布Fi,j(u)、Gi,j(v)也没有改变，唯一变化的是Copula函数。按照Zheng et al.[4]的均方误差优化准则，可得到PBF Copula函数族中的最优分块混合Copula函数C*(u,v)，即PBF Copula族的均方逼近误差为：

(20)

其中：

(21)

(22)

最优分块混合Copula函数则是：

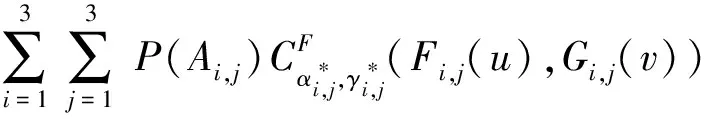
(23)

(三)风险传染定义及传染方向识别

本文已经完成了市场行情的概率划分，并在每一种行情下实现了相关性结构的分解。接下来，本文将给出相关性结构中不同风险效应的分解系数，在此基础上提出新的风险传染度量方法，检验中美股市风险传染效应的显著性并识别两国股市的风险传染方向。通过定义式(12)可以发现，同单调相关意味着中美两国股市受到共同风险因子影响产生同向变动的关系，借鉴Cherubini & Mulinacci[29]的研究，本文将风险传染与同单调相关相对应，如果中美股市间相关性结构分解中同单调相关性占比较大，即认为风险传染效应较大。具体地，以市场处于低迷行情A1,1为例进行说明。在式(18)和式(19)中，如果相关性中同单调相关结构的敏感系数α1,1较大，则意味着相关性变大的趋势增强，发生风险传染的概率加大，因此该系数α1,1用以度量低迷行情下金融风险的传染效应，本文称之为低迷行情时的风险传染系数；同理，如果相关性中反单调相关结构的敏感系数γ1,1较大，则意味着相关性变小的趋势增强，发生风险分散的概率加大，该系数γ1,1用以度量低迷行情下金融风险的分散效应，本文称之为低迷行情时的风险分散系数；而当相关性中独立结构的敏感系数β1,1较大时，金融变量间变动方向不能确定，呈现为独立效应，该系数β1,1用以度量低迷行情下金融风险的独立效应，本文称之为低迷行情时的风险独立系数。

至此，本文分别给出了三种市场行情(低迷、正常和繁荣)下相关性结构的分解系数，接下来借鉴Bradley & Taqqu[5]空间传染的概念，考虑不同市场行情，给出如下风险传染定义：

若低迷市场行情下风险传染系数大于正常市场行情下风险传染系数，即α1,1>α2,2时，本文认为中美两国股市间存在风险传染效应，否则，认为中美两国股市间不存在风险传染效应。

然而，对风险传染的研究除了对风险传染效应显著性的检验，还应包括对风险传染方向的识别。因此，本文借鉴Durante & Jaworski[30]提出的风险传染方向判定方法，基于市场行情概率划分，给出符合本文风险传染定义的传染方向判定方法。具体而言，假设R1和R2分别为中国和美国股指的日对数收益率，本文用α1→2表示中国股市处于低迷行情时其对美国股市的条件风险传染系数，α2→1表示美国股市处于低迷行情时其对中国股市的条件风险传染系数，计算方法如下：

(24)

(25)

在中美两国股市存在显著风险传染的前提下进行风险传染方向的检验。如果α2→1>α1→2，说明美国股市处于低迷行情时对中国股市的条件风险传染系数大于中国股市处于低迷行情时对美国股市的条件风险传染系数，此时认为美国股市对中国股市存在单向风险传染；如果α2→1<α1→2，说明美国股市处于低迷行情时对中国股市的条件风险传染系数小于中国股市处于低迷行情时对美国股市的条件风险传染系数，此时认为中国股市对美国股市存在单向风险传染；如果α2→1=α1→2，说明美国股市处于低迷行情时对中国股市的条件风险传染系数等于中国股市处于低迷行情时对美国股市的条件风险传染系数，此时认为中美两国股市间存在对称风险传染。

三、实证研究

(一)数据选取和描述统计

本文选取2001年1月—2020年7月上证综合指数和标普500指数的日收盘价数据进行实证分析，数据来源于Wind数据库。考虑到跨时区问题，用美国的上一期数据和中国的当期数据一一对应。此外，由于中美两国节假日不同，两地股市的休市规定有所差异，在全样本区间内两大股指数据都存在某些日期的缺失，因此本文剔除了两国不重叠交易日的数据，剩余样本数为4 582个。令R1和R2分别表示上证综合指数和标普500指数日对数收益率，计算方法为Rt=100×Ln(Pt/Pt-1)，运用cubic插值法消除收益率序列中的零值，并进行ADF平稳性检验，检验结果显示，两大指数收益率序列均为平稳序列。从偏度、峰度及JB检验结果可以看出，两大指数的日收益率均不服从正态分布，存在不同程度的尖峰厚尾特征。相比较而言，上证综合指数收益率的均值较小，标准差较大，波动性更强。由于篇幅所限，不再披露具体的实证结果，留存备索。

金融风险天然具有传染特点，只是在不同市场行情下传染强度和可控性有所不同，现实意义上的风险具体是相关性结构中的风险传染效应在市场由正常行情向极端行情发展过程中逐渐增强、积聚，最后导致失控的结果。针对中美两国股市相关性，从长期来看，两国股市同涨同跌的幅度是非对称的，我国股市对美国股市的跟跌特征强于跟涨特征。因此，低迷市场行情下更易产生风险传染，对中美两国股市同跌时的风险传染研究显得尤为重要。本文采用滚动方法对中美两国股指收益率同时进入下尾部区域时的低迷市场行情概率①进行动态趋势分析，设置230天为滚动窗口，1天为滚动步长，图2给出了中美股市低迷市场行情概率的趋势图。

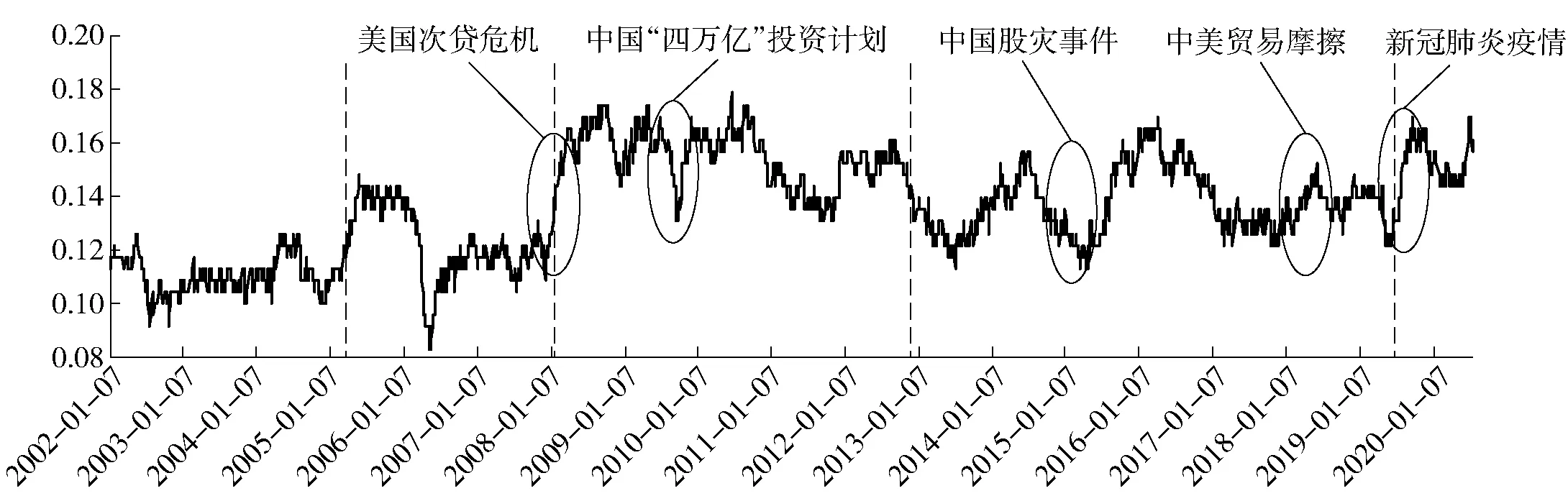
图2 中美股市低迷市场行情概率的趋势

从图2可以看出，低迷市场行情概率的走势形成了几个明显不同的阶段，本文采用传统的均方误差(MSE)方法进行断点检验，确定样本观测期内低迷市场行情概率的断点，以便对整个样本时期进行时段划分。由于整个样本区间近20年，使用MSE方法进行断点检验需要遍历全部样本点，为了符合实际情况且最大限度保证断点检验的效率，本文以2011年为界将样本数据分成两组，两组数据均采用MSE方法进行断点检验。根据低迷市场行情概率的动态趋势图，假设2011年前后两个子样本内各自存在两个断点。因此，针对每个样本阶段，记动态低迷市场行情概率序列为{Pi}，1≤i≤N，断点发生在Pm和Pn，即第一段包含m个样本，第二段包含n-m个样本，第三段包含N-n个样本。定义MSE为：

(26)

当MSE最小时得到最优解m*、n*，即：

(27)

利用Matlab编程，对两个子样本的序列{Pi}进行循环遍历求解，最终得到2002年1月7日—2011年1月3日②，最优解为MSEmin=0.196 4，对应具体时间节点分别为2005年3月8日和2008年1月30日；2011年1月4日—2020年7月21日，最优解为MSEmin=0.246 6，对应具体时间节点分别为2012年11月30日和2019年7月30日。如图2中虚线所示，四个断点将整个样本观测期分为五个时段。为了检验MSE方法得到断点的稳健性，本文同时采取Mann-Kendall突变检验方法③对低迷市场行情概率序列进行检验，由于Mann-Kendall突变检验分析采用年度数据检验效果最符合现实，得到突变点为2006年12月31日、2012年12月31日和2019年12月31日，基本能够对应2008年1月30日、2012年11月30日和2019年7月30日，样本子区间划分基本具有稳健性。由于2005年后中国股市逐渐对国际股市产生影响，不再为“独立市”，本文仍保留2005年3月8日为断点。接下来，计算各时段中美股市低迷市场行情概率的均值及标准差，如表1所示。

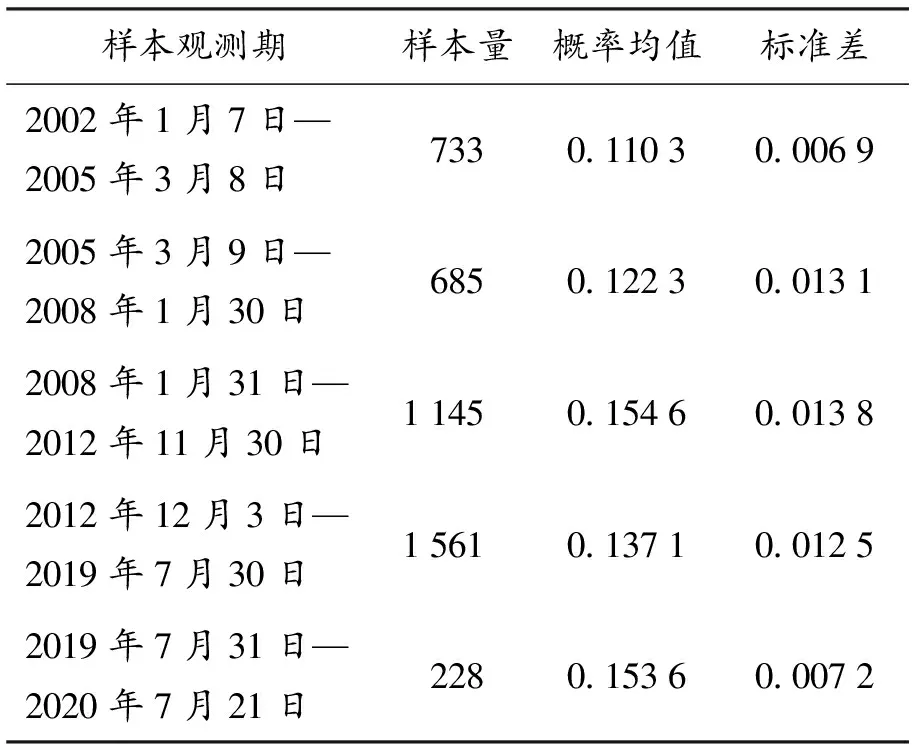
表1 分时段低迷市场行情概率均值及标准差

根据MSE方法得到的断点可以将整个样本观测期划分为五个时段，每个阶段均包含对中美两国股市具有重大影响的事件。例如，第一时段涵盖了中国加入世界贸易组织事件，以及中国资本市场逐渐对外开放；第二时段从2005年中国人民币汇率改革至2008年美国次贷危机爆发前夕；第三时段涵盖了整个美国次贷危机高潮期，在此期间中国实行“四万亿”投资刺激计划以缓解次贷危机对国内经济的冲击；第四时段涵盖了中国股灾事件及中美贸易摩擦；第五时段涵盖了新冠肺炎疫情及沙特石油价格战事件。从各阶段低迷市场行情均值来看，第三时段次贷危机时期中美股市呈现低迷市场行情的概率最大，且波动幅度最大，说明该时期发生风险传染的可能性最大。结合实际重大事件发生的时间点，可以看出图2中市场行情低迷的概率在美国次贷危机、中国“四万亿”投资计划、中国股灾事件、中美贸易摩擦和新冠肺炎疫情等几个重要事件前后均有异动，表现出一定的灵敏性。

(二)中美股市风险传染效应分析

1.中美股市相关性结构中风险传染效应的动态分析

与正常市场行情相比，极端市场行情的风险传染更容易失控。因此，本文基于分块混合Copula模型对极端市场行情下中美两国股市间的相关性结构进行动态分析，设置230天为滚动窗口，1天为滚动步长，滚动得到中美股市相关性结构中风险传染效应和风险分散效应的动态趋势图，参见图3。

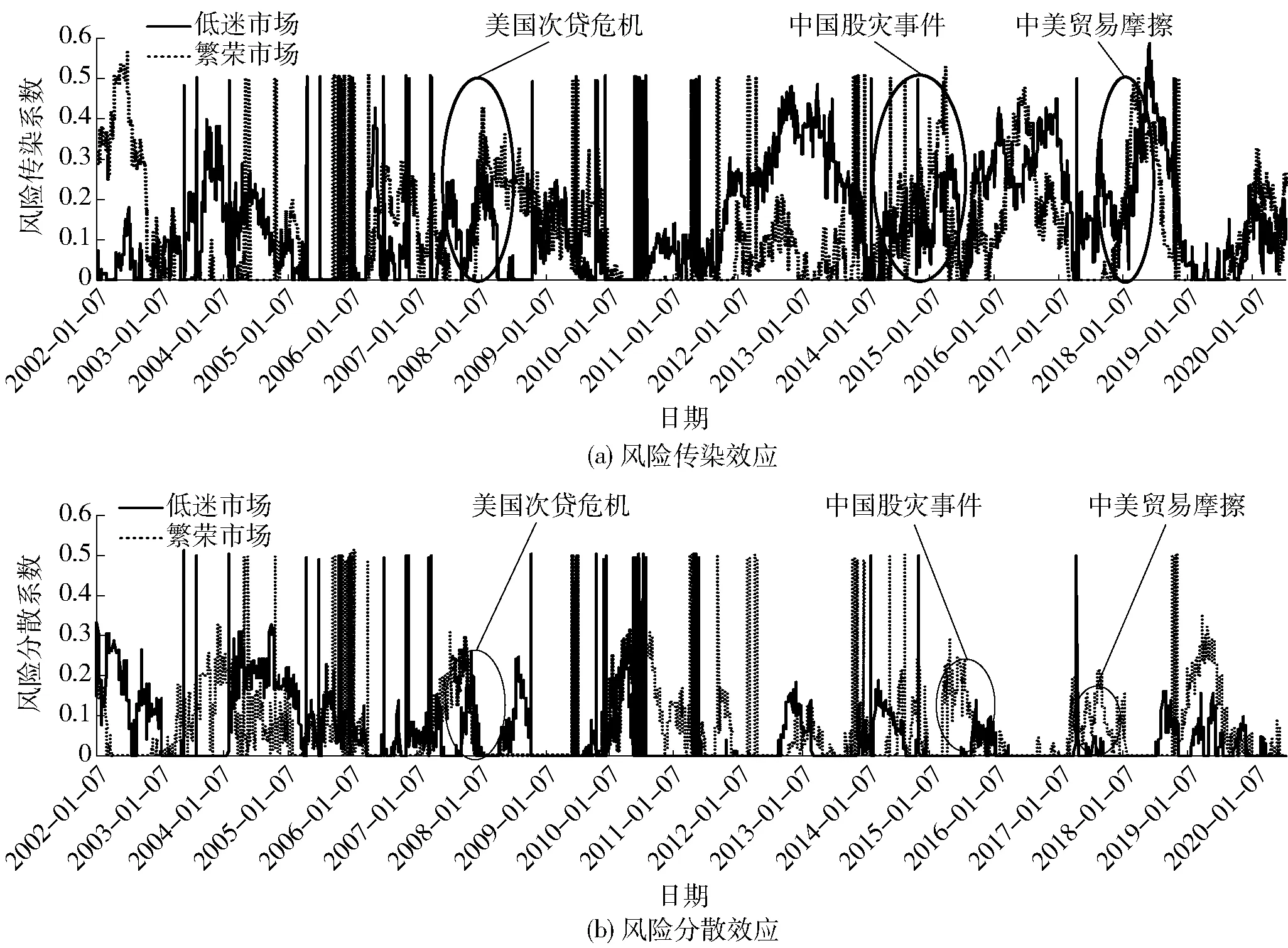
图3 极端市场行情(低迷市场行情和繁荣市场行情)风险效应

不难发现：第一，低迷和繁荣两种极端市场行情下的中美股市相关性结构有相似之处，即风险传染系数和风险分散系数均呈现密集的脉冲式跳动现象，并且出现的时间节点为市场预期发生明显改变的前夕，由此表明，极端市场行情下的两类风险效应对重大危机事件具有一定的敏感性。第二，中美股市相关性结构中的风险传染效应和分散效应在两个极端行情中呈现非对称性，纵观整个样本时期，由图3(a)发现大部分时间内低迷市场行情的风险传染系数高于繁荣市场行情的风险传染系数；而风险分散系数则相反，由图3(b)发现大部分时间内繁荣市场行情风险分散系数高于低迷市场行情的风险分散系数。第三，风险传染和分散效应在重大危机事件发生时的表现完全不同。例如，在2008—2009年次贷危机、2015年中国股灾事件、2018年中美贸易摩擦这些重大危机事件持续期间，低迷市场行情的风险传染系数急剧上升，而此时低迷市场行情的风险分散系数却维持在较低的水平，表明重大危机事件发生时中美股市之间的风险传染可能性很大，风险缓释的可能性较小。第四，由图3(a)可以看出，次贷危机以后低迷行情时的风险传染效应和繁荣行情时的风险传染效应表现出同步性，即低迷行情的风险传染系数增大，繁荣行情的风险传染系数也增大；低迷行情的风险传染系数降低，繁荣行情的风险传染系数也降低。

为进一步验证上述结论，本文同样设置230天为滚动窗口，1天为滚动步长，分别计算了两个极端行情下的风险传染系数的spearman相关系数，参见图4。

图4 极端市场行情下风险传染效应相关性

由图4可以看出，极端市场行情下风险传染效应相关性整体呈现波动上升趋势。自中美贸易摩擦发生以来，中美股市在极端市场行情下的风险传染效应相关性很强且始终为正，这说明极端市场行情下中美股市的风险传染效应的关联性增强，即低迷与繁荣两种行情下的风险传染效应将以较大概率伴随出现。

2.中美两国股市风险传染效应检验

基于前文对极端市场行情下中美两国股市相关性结构中风险传染效应和分散效应的动态研究，本文进一步分析极端市场行情下两种风险效应的特征。根据前文对中美股市低迷市场行情概率的断点检验结果划分整个样本时期，计算极端市场行情下不同样本时段风险传染效应和分散效应的均值及标准差，结果如表2所示。

不难发现：第一，低迷和繁荣市场行情下风险传染系数的均值在次贷危机之后显著增加，表明中美股市之间的风险传染效应显著增强；而风险分散系数的均值及标准差呈减小趋势，表明中美股市之间的风险分散效应逐渐弱化。第二，低迷和繁荣行情下风险分散系数均值基本小于对应时间段内的风险传染系数均值，表明中美股市之间较大概率表现出风险传染特征。第三，低迷行情下的风险传染系数基本大于对应时间段内繁荣行情下的风险传染系数；风险分散系数则相反，低迷行情下的风险分散系数基本小于对应时间段内繁荣行情下的风险分散系数，也印证了低迷市场行情爆发风险传染的可能性更大。

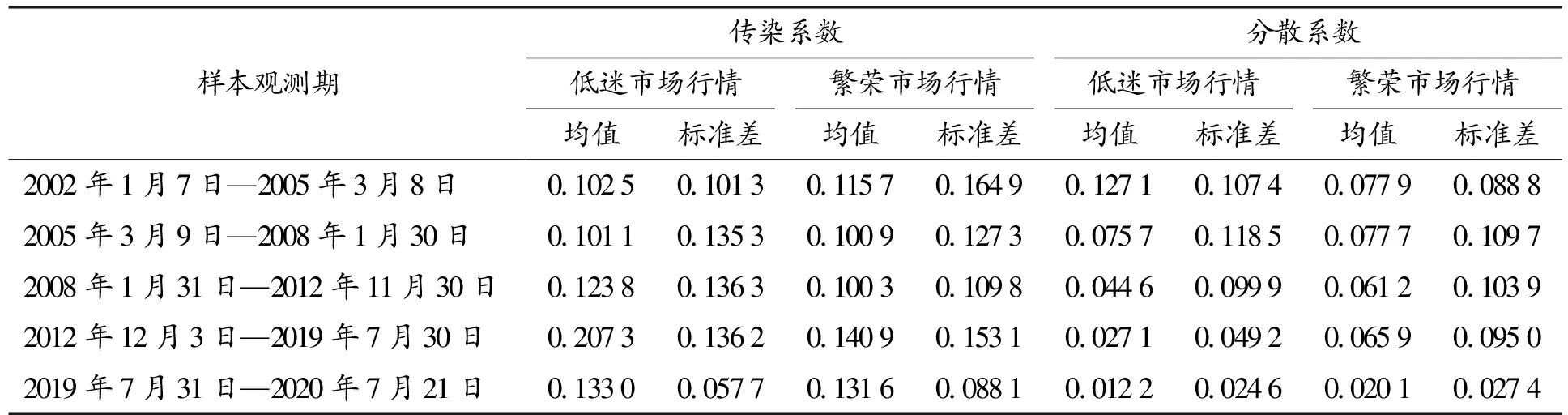
表2 极端市场行情下风险效应的均值及标准差

根据上述分析，本文以低迷市场行情下的风险传染系数为标准，依据前文断点检验的结果，检验不同样本时段里中美股市是否存在显著的风险传染效应，即对各时段低迷行情风险传染系数α1,1和正常行情风险传染系数α2,2差值进行T统计量显著性检验，显著水平设定为1%。给出如下原假设及备择假设。

H0：α1,1-α2,2≤0

H1：α1,1-α2,2>0

其中，H0为原假设，即中美股市间不存在风险传染效应；H1为备择假设，即中美股市间存在风险传染效应。T统计量检验结果如表3所示。

可以看到：虽然中国在2001年就加入世界贸易组织，积极参与全球化进程，但是在2005年以前，中美两国股市低迷行情风险传染系数与正常行情风险传染系数差值不大。因此，本文在该时段内不能拒绝原假设，表明该时段中美股市之间不存在显著的风险传染效应。2005年以后的4个时段，中美两国股市均存在不同程度的风险传染效应。2005年以后，中国股市与发达国家股市的相互影响关系逐渐增强，2005—2008年中美股市开始存在显著的风险传染效应。2008年美国次贷危机席卷全球，股票价格暴跌，投资者心理预期、羊群效应等也加速了风险的传导。自从2013年中国提出“一带一路”倡议，提议筹建亚洲基础设施投资银行，中国资本市场实力逐步增强。亚投行的顺利建成使得中国在推进“一带一路”倡议并与周边国家积极加强互联互通的过程中取得重大进展，因此2012—2019年中美股市之间风险传染效应最强。随着中国对外开放进程的不断推进，外资持有A股比例不断上升，2018年以来，中美两国展开多次贸易磋商，引起中国A股市场波动剧烈，中美股市风险传染效应持续存在。

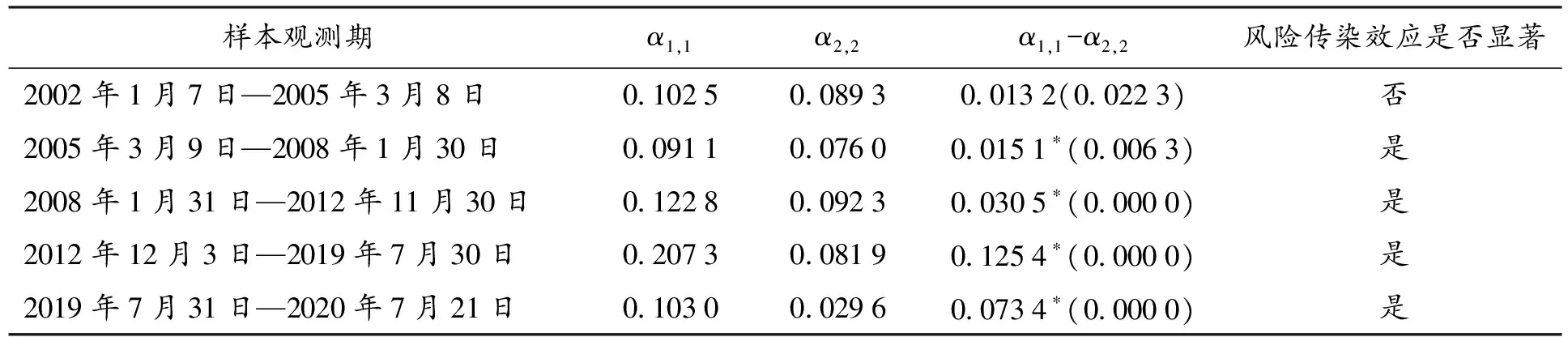
表3 五个时段中美股市风险传染效应显著性检验结果

3.中美两国股市风险传染方向检验

想要全面掌握中美股市间的风险传染情况，除了对二者之间的风险传染效应进行研究外，还必须准确识别二者之间的风险传染方向。因此，本文基于市场行情的概率划分，根据式(24)和式(25)计算条件风险传染系数之差，即α2→1-α1→2，做出中美股市风险传染方向的判断。为了直观判断两国股市准确的风险传染方向，同样设置230天为滚动窗口，1天为滚动步长，绘制中美股市之间条件风险传染系数之差的动态趋势图，如图5所示。

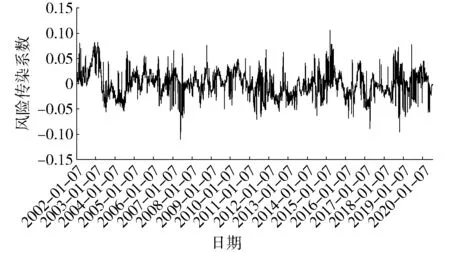
图5 中美股市风险传染方向动态趋势

可以看到，2003年之前，两国股市表现出美国向中国的单向风险传导，2003年之后，中美股市间的风险传染方向处于不断变化之中，而随着中国逐渐提高资本市场对外开放程度，中国股市也表现出一定的影响力，即中国股市开始短时内向美国股市传导风险。2012年以后，中国股市越来越频繁地向美国股市传导风险，且时间跨度也逐渐增加，足以表明中国市场开始在国际市场上发挥影响力。

由于前文对风险传染效应的显著性检验认为2002—2005年，即第一时段，中美两国股市不存在显著的风险传染效应，接下来，本文仅针对两国股市存在显著风险传染效应的四个时段，定性识别每个时段内的风险传染方向。本文采用α2→1-α1→2差值的T统计量显著性检验，显著水平设为1%，给出如下原假设及备择假设。

H0：α2→1-α1→2=0
H1：α2→1-α1→2≠0

其中， H0为原假设，即中美股市间存在对称风险传染；H1为备择假设，即中美股市间存在单向风险传染。若α2→1-α1→2均值显著大于0，则表明美国股市对中国股市存在单向风险传染；若α2→1-α1→2均值显著小于0，则表明中国股市对美国股市存在单向风险传染。T统计量检验结果如表4所示。

可以看出，中美股市风险传染方向经历了两次更迭，2008年次贷危机高潮之前，美国经济发展迅猛，对中国经济造成压力，此时两国股市表现为美国股市对中国股市的单向风险传染。2008—2012年间，经历了次贷危机的剧烈冲击，美国经济发展趋势放缓，中国实施“四万亿”投资计划缓冲次贷危机对国内经济的冲击，因此这段时间内中美股市呈现对称风险传染。2012—2019年，随着2013年中国提出“一带一路”倡议，国际范围内中国持续扩大经济影响力，中国股市开始向美国股市传导风险，风险传染方向发生改变。近两年，中美贸易摩擦持续升级，使国内经济承压，2019年年底暴发新冠肺炎疫情，恰逢沙特发起石油价格战，原油期货价格暴跌，多重因素作用下，美股指数在2020年3月的8个交易日内触发4次熔断机制，引发投资者恐慌，美国股市再次向中国股市释放风险传染。

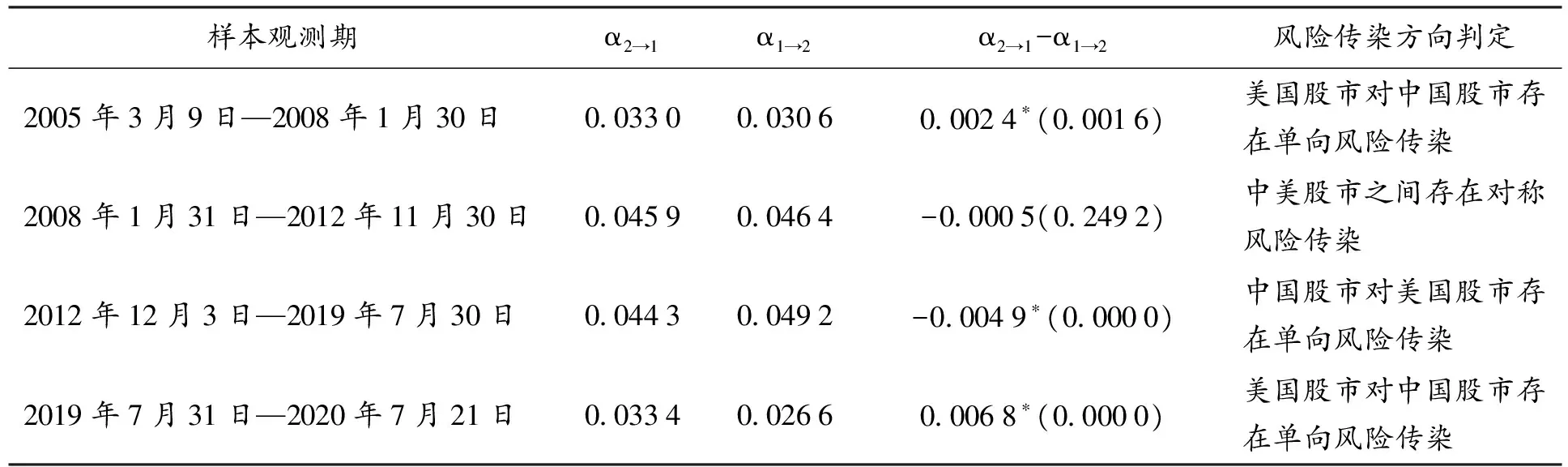
表4 四个时段中美股市风险传染方向显著性检验结果

四、研究结论与启示

金融市场间的风险传染效应研究是金融风险研究的重要基础。针对中美两国股市相关性及风险传染之间关系的问题，本文基于分块混合Copula模型，实现不同市场行情下中美股市间相关性的结构分解，区分相关性结构中不同的风险效应，给出一种新的风险传染效应度量及识别方法，从风险传染效应的显著性和方向性识别两个角度深入研究中美股市之间的风险传染现象，得到如下结论：

首先，通过对相关性结构中不同风险效应分解系数的动态分析，发现风险传染和风险分散效应在低迷和繁荣两种市场行情下呈现非对称性。具体来看，整个样本期间大多数时间内低迷市场行情的风险传染系数高于繁荣市场行情的风险传染系数；而风险分散系数则相反，大多数时间内繁荣市场行情风险分散系数高于低迷市场行情的风险分散系数。

其次，通过对中美股市两种极端市场行情下风险传染系数相关性的动态分析，发现近几年来极端市场行情下中美股市之间的风险传染效应关联性增强，低迷市场行情时的传染效应和繁荣市场行情时的传染效应表现出同步性，即低迷与繁荣两种行情更迭时，风险传染效应有较大概率伴随出现。

再次，通过对中美股市相关性结构进行分解，给出适用于风险传染系数的风险传染定义，对全样本区间和不同时段中美股市风险传染效应进行T统计量显著性检验，发现2002—2005年，即第一时段内，中美股市间不存在显著的风险传染效应。2005—2020年的4个样本时段内，中美股市之间均存在不同程度的风险传染效应，且2012—2019年两国股市之间风险传染效应最强。

最后，从风险传染方向上看，结合市场行情因素，利用条件风险传染系数之差作为中美股市风险传染方向的判别指标，次贷危机前，美国股市整体表现为风险传染主导，次贷危机高潮期间，中国采取一系列救市政策，中美股市表现为对称风险传染。随着2013年中国提出“一带一路”倡议，中国股市甚至一度表现出对美股的传染效应，两国风险传染方向发生转变。2020年，新冠肺炎疫情暴发及沙特发起石油价格战这两大“黑天鹅”事件，导致美股波动剧烈，两国风险传染方向再次发生转变，美国股市再次占据风险传染主导地位，呈现对中国股市的单向风险传染。

本文通过对中美两国股市风险传染效应的研究，可知中美股市在一定程度上存在风险传染效应，且两国股市之间风险传染方向发生了两次转变，正确识别中美股市间的风险传染方向，有利于政府当局以及风险管理者对金融风险进行有效的监管和防范。此外，本文也存在一些不足，根据本文实证结论，2005—2020年，中美股市存在显著的风险传染效应，但不同样本时期可能存在多种风险传染渠道的共同作用，如金融关联渠道、贸易关联渠道以及经济实体间的非实质关联渠道等，引发风险传染效应的原因和传导机制未必相同，接下来的研究中，作者将对中美股市风险传染效应这一问题进行有针对性的深入探索，如两国股市风险传染的原因、传染机制的特征和规律等，以期为金融风险管理等一系列重大问题提供有益补充和参考。

注 释：

①根据图1，两国股指收益率均处于下尾部区域的市场行情称为低迷市场行情，即A1,1代表低迷行情，其概率为P(A1,1)=P(U≤1/3,V≤1/3)。

②2011年样本的起始点为1月3日。

③Mann-Kendall突变检验方法比较复杂，且不是本文研究重点，此处不做展开赘述，如需要稳健性结果可联系作者。作者邮箱：luanxinljca@163.com。