位山灌区输沙渠泥沙运移特性研究

马 强，徐立荣，董晓知，徐 晶

(济南大学 水利与环境学院，山东 济南 250022)

黄河是世界上输沙量最大和含沙量最大的河流，因此引黄灌区具有“引黄必引沙”的重要特点[1]。引黄灌区自开始引水以来，泥沙问题一直伴随着灌区发展[2]。虽然自2002年小浪底水库进行调水调沙试验，并转入正式生产运行后，黄河下游特别是山东境内的引黄条件发生了很大变化，如引黄能力下降，输沙量变小等，但是引黄灌渠排沙问题仍未减轻，如何排沙依旧是黄河下游治理的重中之重，需要重新提出科学的水沙调度和合理的工程措施，从而延长沉沙池使用寿命，减少骨干渠道淤积，更好地发挥灌区的灌溉效益。

渠道是灌区灌排系统组成的重要部分，而渠道输水输沙能力的有效实现是整个灌区正常运行的关键[3-4]。为了解决灌区的泥沙问题，提高渠道的输水输沙能力，减少泥沙淤积，保证灌区的正常运行，人们通常以控制渠道泥沙淤积为目标，建立相应水沙数学模型。一般对河道泥沙淤积的数学模型研究多采用一维水沙模型，模拟断面各水沙要素的总平均值[5]，相比之下，平面二维水沙模型能更清楚地表达河床的平面变形，因此被广泛应用于河道水沙运动研究[6-7]。

目前，对于引黄灌渠输沙渠道二维水沙的泥沙淤积研究成果较少。本文中以山东省聊城市位山灌区一支改造后的输沙干渠——东输沙渠作为研究对象，以控制输沙渠渠道泥沙淤积为目标，利用水力学模型MIKE 21具有的简单、快速、精确、可视性好等优点[8]，构建输沙渠二维水沙模型，在经过模型率定与验证后，设计典型工况对水流特性及泥沙淤积分布规律进行模拟预测，筛选保水输沙的最佳方案，为黄河下游引黄灌区干渠泥沙治理和利用提供参考。

1 研究区概况

山东省聊城市位山灌区地处黄河下游，是全国第五大灌区、山东省最大灌区[9-10]。灌区共包括四区一市五县，土地总面积为5 380 km2，总耕地面积为3 793 km2，设计灌溉面积为3 387 km2[11]。灌区南靠黄河，北临卫运河，东与山东省德州市相接，马颊河和徒骇河从灌区自西南向东北贯穿而过。灌区属黄河冲积形成的平原，地势平坦开阔，走向略微向东北方向倾斜[9，11]。

东输沙渠于2019年改造完成，全长14.5 km，担负着一干渠供水供沙的任务，具体位置如图1所示。东输沙渠下接进入东沉沙区，有沉沙池3个，已还耕1个，主要使用1#、3#池轮用，2个沉沙池长度分别为3.0、3.2 km。渠道断面被改造成梯形复式断面，为了使水流顺畅、流态稳定，渠道中心线保持不变。渠道比降仍采用原比降1/6 000，边坡坡比为1∶2.0，复式断面底宽为16.0 m，渠道开挖深度为1.5 m，浅滩宽度为2 m。

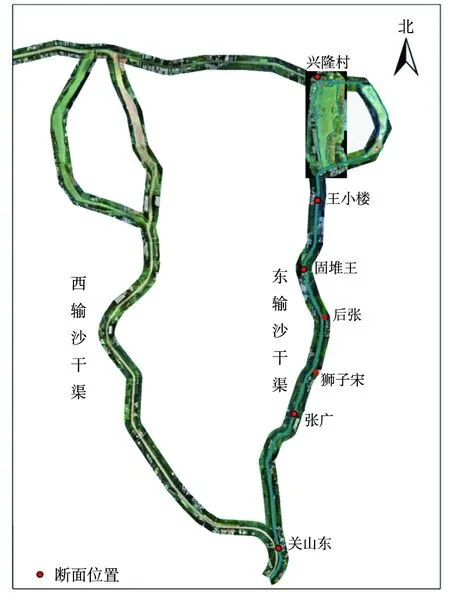
位山灌区地理位置地图从国家测绘地理信息局标准地图服务网站下载，地图审批编号为GS(2019)3333(http://bzdt.ch.mnr.gov.cn/browse.html?picId=%224o28b0625501ad13015501ad2bfc0210%22)，经过ArcGIS10.3软件数字化处理得到。图1 位山灌区输沙干渠图

2 二维水沙模型建立及验证

2.1 水动力模型理论

水力学模型MIKE 21中的水动力(HD)模块是必需选择的核心模块，是所有模拟的基础。该模块建立在基于二维数值求解方法的浅水方程基础上，在深度上集成了三向不可压缩雷诺(Reynolds)平均Navier-Stokes方程，并服从Boussinesq假设和静水压假设[12-15]。

二维非恒定浅水方程组包括连续性方程，X、Y方向动量方程，即

连续性方程

(1)

X方向动量方程

(2)

Y方向动量方程

(3)

该模型是由动量守恒方程和水流连续方程组成，在水平面上可以使用笛卡尔坐标。

2.2 泥沙模型理论

水力学模型MIKE 21中的输泥模块(MT)结合了多粒径级和底床分层，描述了黏聚性泥沙(淤泥或黏土)在波浪和水流作用下的冲刷、传输和沉积[16]。

1)基本方程。二维输泥模块的对流扩散控制方程为

(4)

2)泥沙沉积过程。泥沙在水体中通常处于沉积和悬浮状态，泥沙淤积是泥沙颗粒从水体沉降至床面的输移过程。当床面切应力小于淤积临界切应力时，产生泥沙淤积；反之，床底发生冲刷。细颗粒泥沙的沉降速度取决于颗粒大小、温度、泥沙浓度等。黏性泥沙的淤积的控制方程为

D=ωsρbPD，

(5)

式中：D为沉积率；ωs为泥沙沉降速度，m/s；ρb为泥沙的近底质量浓度，kg/m3；PD为泥沙沉降在河床的概率函数，

(6)

其中τb、τcd分别为河床剪切应力、河床淤积临界剪切应力，N/m2。

3)河床的冲刷过程。河床剪切应力τb大于临界冲刷剪切应力τce时，就会发生河床层的冲刷。床底冲刷程度表达式为

(7)

式中：SE为侵蚀率；E为床底冲刷程度，kg/(s·m2)；n为侵蚀程度。

2.3 模型的建立

2.3.1 模型的范围与网格

模型范围是上起位山闸口(东经116.122 905°，北纬36.141 67°)，下至东沉砂池入口(东经116.142 618°，北纬36.264 66°)。

河段冲淤演变计算所采用的网格划分为普遍用于各种河道的非结构三角网格，渠道边界条件简单，因此不对网格进行局部加密，河道形态存在弯道河段，模拟计算时间设置为30 d。经过反复试算，网格划分参数设置如下：三角网格边长为6 m，网格总个数为35 012，总节点个数为19 919，最终网格文件由网格生成器生成，如图2所示。

2.3.2 边界条件及参数设置

模型计算采用上游位山引黄闸处流量及含沙量作为进口边界，东沉沙池入口处水位作为下游出口边界，模拟总时间步长为3 600 s，设置时间步数为700，空间和时间的积分都采用低阶、快速运算(low order，fast algorithm)的求解格式来求解浅水方程。模型建立完毕后，进行水动力模块和泥沙运输模块的参数设置，见表1。

表1 水动力模型边界条件与模型参数设置

2.4 模型验证

模型验证的目的是检验所建模型与实际工况的相似度，对模型中相关参数的率定结果进行检验和修正。

2.4.1 水动力模块验证

位山灌区多年没有发生洪水，只存在关闸不引水而断流的情况，河道经历了开挖、淤积、清淤、改造，处于不断变化的过程，缺乏长系列配套的水文地形资料。对于2019年下半年改造后的东输沙渠，根据现有的水文资料情况，主要验证内容为沿程水面线。使用改造实施方案中的设计规划图所规定的渠底高程、设计水位及典型断面的构造等数据为验证参数，最终得出验证水面线和设计水面线的数值，见图3。由图可以看出，经过多次的率定验证后，二维水动力模型输出的模拟计算水位与河道设计水位相比，水位值存在较小正负偏差，水位的绝对误差为0～0.07 m，均方根误差(RMSE)为0.054，水面线的验证模拟计算结果与河道设计水位过程线基本吻合，整体误差较小，模型拟合度较好，表明模型的构建及参数设定合理。

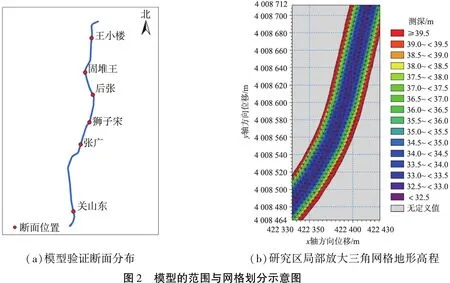
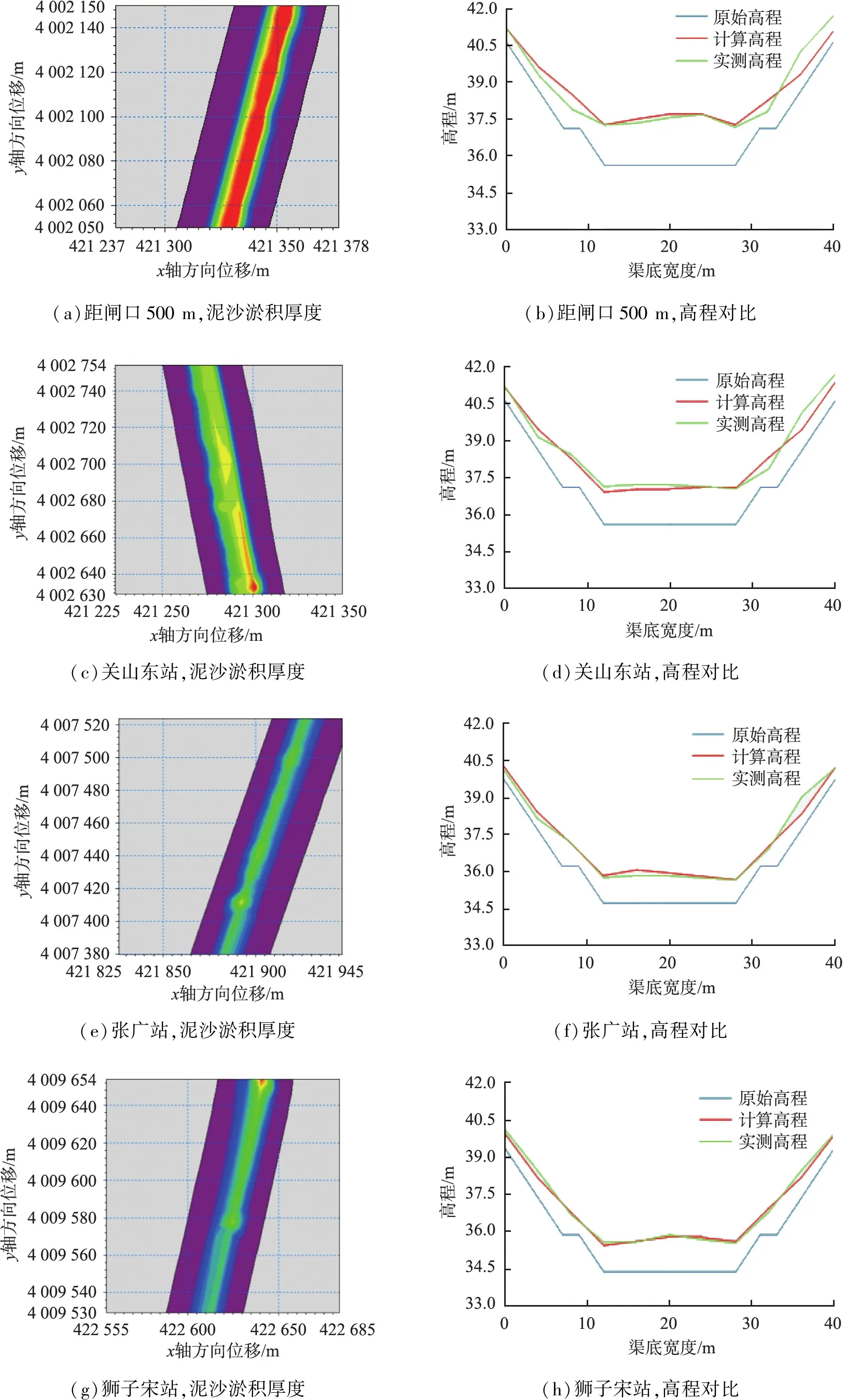
在各典型断面的站点附近上、下游200 m处为起点、终点截取水位图，如图4所示，在关山东站(距闸口1 100 m)水位为38.2～38.4 m，张广站(距闸口5 846 m)水位为37.4～37.6 m，狮子宋站(距闸口8 000 m)水位为37.2～37.4 m，后张站(距闸口10 000 m)、固堆王站(距闸口10 900 m)水位为37.0～37.2 m，王小楼站(距闸口13 290 m)水位为36.6～36.8 m，模拟计算结果合理，符合水流运动规律，该模型可以用于下一阶段对泥沙数值模拟及预测。

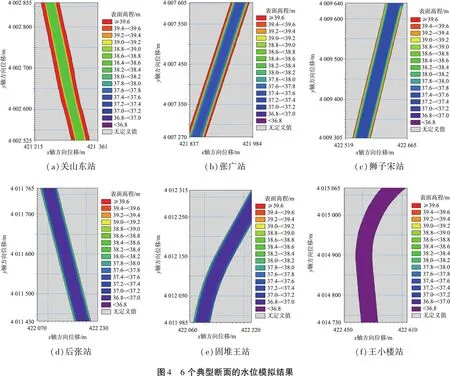
2.4.2 泥沙模块验证

截取渠道的6个典型横断面模拟淤积1 a后的泥沙淤积厚度进行对比分析(见图5)。由图可以看出，最大泥沙淤积厚度为2.0 m，红色区域淤积情况最为严重，主要淤积分布在自闸口至距闸口500 m处渠道中线处，渠道中段的淤积厚度在1.2～1.5 m之间，渠尾的平均淤积厚度为1.0 m。同一断面的淤积先在地形高程较低的位置形成，在两侧原渠底的部分淤积厚度为0.52～0.86 m，中间新建挖深后子槽渠底的淤积厚度为1.12～2.17 m。从各断面渠底高程、实测高程与计算高程的对比可以看出，淤积量计算高程线基本拟合于实际测定高程线，演变态势大致相同，表明耦合泥沙模块后的数学模型计算的淤积量与横截面上的实际淤积量基本吻合。

所建立的泥沙数学模型基本上可以反映东输沙渠的冲淤演变规律，整体趋势符合较好，冲淤量计算结果与实测结果相近，可应用于研究不同流量下东输沙渠的冲淤过程中水流沿程变化及横向、纵向泥沙淤积分布及淤积量的变化。

3 不同方案冲淤数值模拟对比

根据东输沙渠水位及流量关系，以水流条件作为自变量，分别选取设计流量为10、20、40、60 m3/s对应的水位，由实测资料及合理率定得出，具体计算工况条件见表2。

表2 模拟工况数据设置

以率定验证后的水动力泥沙耦合模型作为工具，根据4种方案的流量水位作为起始条件运行模型，得到4种预测情景下东输沙渠流速、水位和含沙量等模拟数据，观察运行过程中水流条件沿程变化、河道主流变化情况、淤积体平面淤积形态及其变化过程以及横断面淤积特性。

3.1 水流特征变化

模拟东输沙渠不同方案时的泥沙淤积过程，提取整条渠道流速、水位沿程变化曲线，结果如图6所示。4个方案的渠道中段距闸口6 000～10 000 m处的平均流速依次为0.527、0.648、0.868、1.103 m/s，流速随流量增大而增加。由于流速受过水断面的影响，因此在同一流量时整体的渠道流速有所减小，距闸口5 000 m处的流速有小幅增加，原因是中游区域断面的过水面积有所减小，但实际过流面积变化率不大，流速增幅仅为0.10～0.15 m/s。方案1的流速沿程变化幅度不大，方案2的流速有沿程逐渐减小的趋势但波动不明显，方案3、4的流速变化趋势相似，均是上段流速相对较大，下段流速相对较小，流速变化最大的位置大致相同。

图6 不同方案的淤积后流速沿程变化

4个方案的水体流向、水体流速变化趋势基本保持一致。引水口附近无漩涡，整个河道上也没有出现漩涡和回流，流态比较平稳。图7是距闸口5 000 m处的局部水力特性图，清晰地展示在不同方案下渠道中段区域的水流速大小及流向。由于渠道较为平直单一，弯道处的曲率半径较大，因此整体流速变化幅度不大，流向没有变化。

不同方案的淤积后水面线沿程变化如图8所示。由图可见，除方案1外，渠道入口周围的水流受河岸边界的影响产生壅水，绝大部分水流集中到渠道中，随着渠道底坡的沿程降低变化，河道水面高程逐渐降低，渠道内部水面高程均匀下降，水位高程降低速率大致相同，距闸口4 500 m处为转折点，出现较大水位变化，在该段出现水位下降的原因主要是河道主流出现侧向收缩，水位的下降速率增大。由于渠道引水流量的增加，河道水面线随着流量的增加不断抬升，渠道距闸口5 000～8 000 m处的渠道的中间段水位抬升幅度较大，其中方案4最为明显，最大水位值出现在距闸口6 000 m处，随着流量的增加，方案3、4的水位抬升幅度分别为0.81、0.68 m，渠道下游距出口2 000 m抬升幅度逐渐减小。由于方案1的水位受到泥沙淤积厚度的影响，因此变化规律与其他3个方案不同，水面线降低幅度较大，前后水位相差3.6 m。

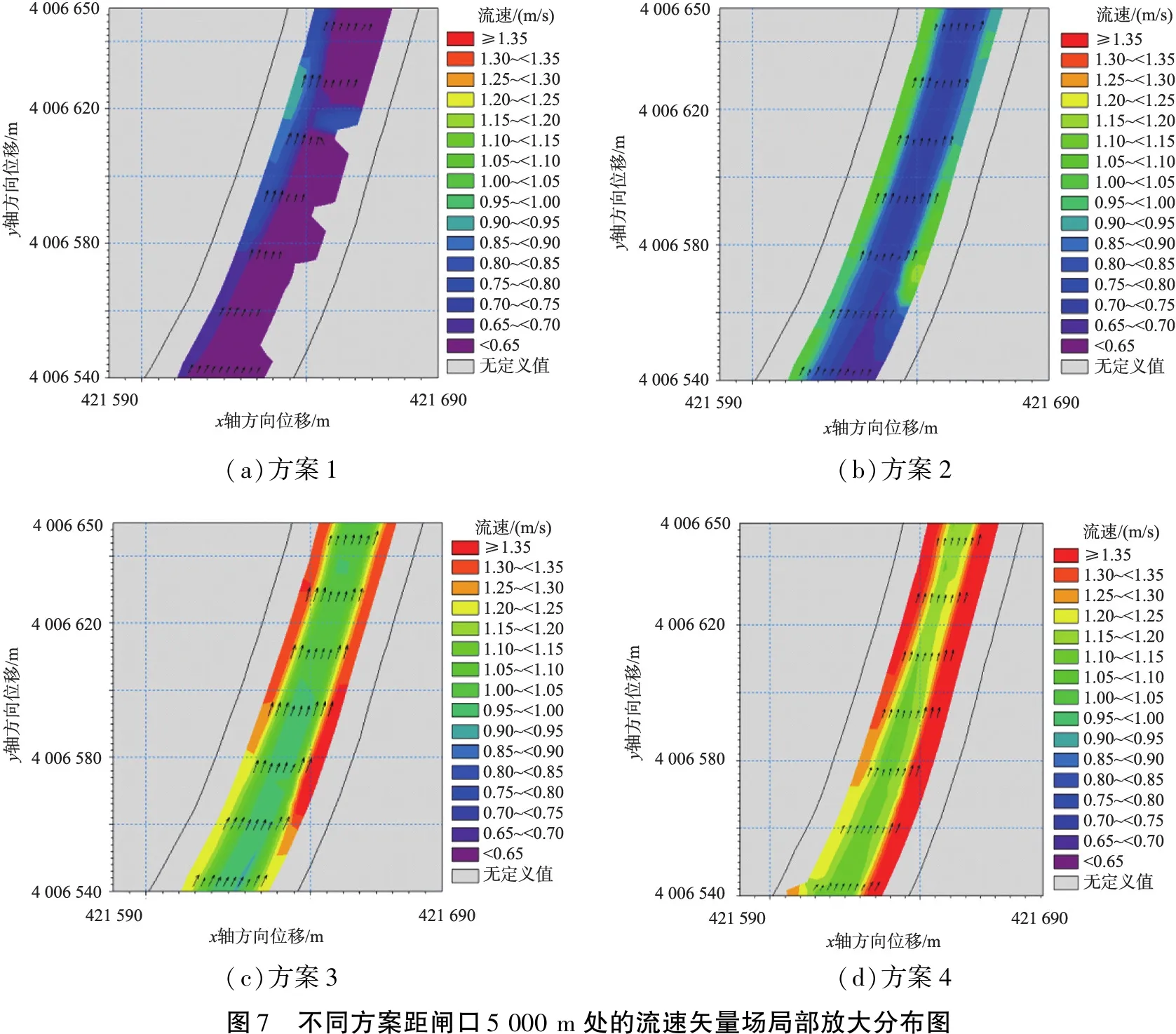
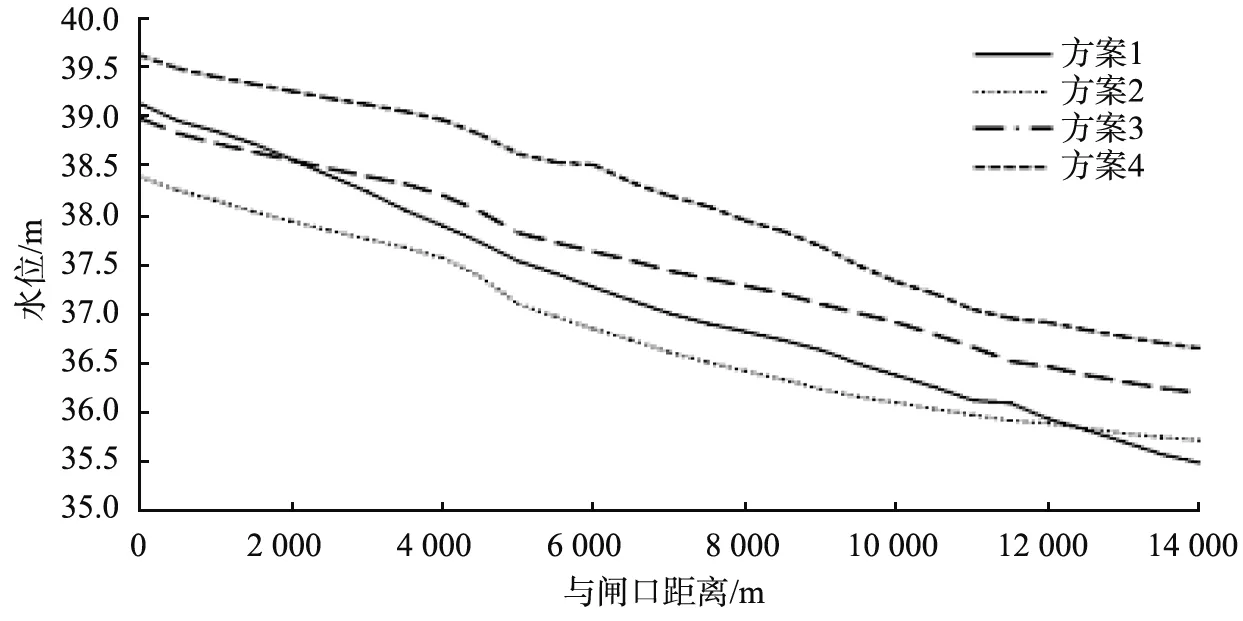
图8 不同方案的淤积后水面线沿程变化

3.2 泥沙淤积特征变化

3.2.1 泥沙淤积纵向特征变化

泥沙淤积纵向形态的发展直接体现了渠道沿程被泥沙侵占的过程及纵向分布。不同方案提取的渠道内等距的纵向深泓点沿程变化如图9所示。从图中可以看出，在入口起至闸前500 m处是淤积最为严重的地区，方案1的深泓点的淤积高度最高达2 m，方案2的淤积高度为0.5～1 m，方案3、4淤积不明显。距闸口1 000～12 200 m是渠道的稳定冲淤范围，方案1的泥沙的形态最为明显，淤积高度从1.6 m到1.0 m逐层向后递减，方案2的泥沙沿程淤积较为均匀，淤积厚度为0.1～0.2 m，在8 000～10 000 m有冲刷的现象。方案3、4的沿程淤积较少，渠道多存在冲刷现象，渠道内泥沙淤积厚度最大为0.1 m左右。流量增大后，渠道内的泥沙显著减少。通过对比分析整个纵断面的河床淤积变化，可以看出方案3、4的淤积较为均匀、稳定。

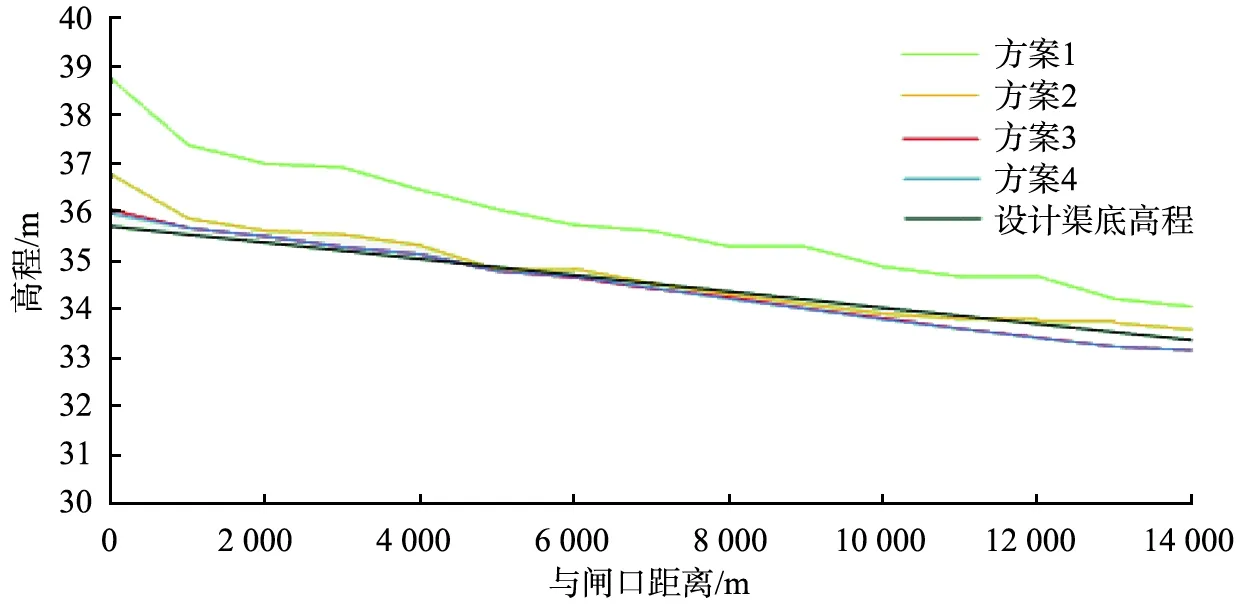
图9 不同方案的渠道纵向深泓点高程变化

3.2.2 泥沙淤积总量特征变化

泥沙随水流从闸口进入渠道后，一部分随水流向前流动，当淤积剪切应力小于临界淤积剪切应力后开始出现沉积，一部分泥沙在渠底淤积，闸后至500 m处渠道前段的泥沙淤积量较大，之后渠道中后段含沙量逐渐减少，泥沙悬浮量较少，水流携带细颗粒泥沙沿河槽向前输移，在渠道处呈点状或片状扩散的趋势，待流速稳定过后落淤至渠底，泥沙的淤积量也相应减少。

流量的加大使得这一过程的水流携带的泥沙大部分处于悬浮状态，流量为60 m3/s时还可能对渠底形成冲刷，渠道内泥沙淤积较少，水流将携带混合大量泥沙，最后将泥沙送至沉砂池发生沉降。

4个方案的泥沙淤积量计算结果见表3。从表中数据可看出，最大、最小淤积高程都随着与闸距离的增加而减小，与渠道渠底高程有关，随着流量的增大相同河段的淤积量不断减少，方案3、4之间的变化不明显。淤积厚度中，除方案1渠前段最大，大量泥沙在渠首充分落淤，其余3个方案均是后段大于前段和中段。方案1的平均淤积厚度大于1 m，泥沙淤积严重，方案3、4的淤积厚度达到较为理想状态。方案2的泥沙淤积量比方案1的大253 723 m3，方案3的泥沙淤积量比方案2的大35 167 m3，方案4的泥沙淤积量比方案3的大12 173 m3，方案3、4的累积淤积变化量最小，大流量下的泥沙淤积在渠道内的部分较少。

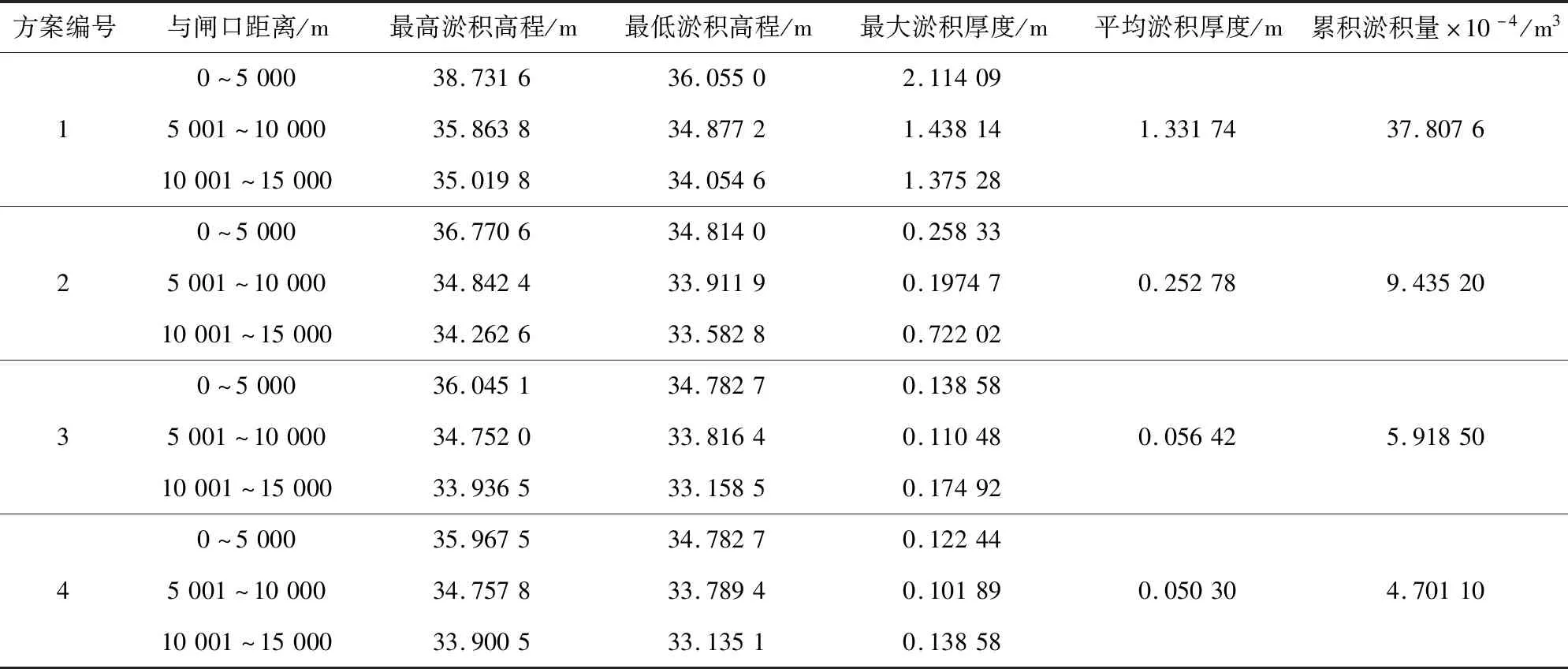
表3 不同方案的泥沙淤积计算结果

4 结论

1)本文中基于水力学模型MIKE 21构建了二维水沙模型，首先对水动力模块进行率定和验证，模拟计算水位与河道设计水位值的绝对误差为0～0.07 m，均方根误差为0.054，模拟计算结果与河道设计水位过程线基本吻合，模型的构建及参数设定合理；其次对泥沙模块进行率定和验证，淤积量计算高程线基本拟合于实际测定高程线，演变态势大致相同，耦合泥沙模块后的数学模型计算的淤积量与横截面上的实际淤积量基本吻合，表明水流与泥沙模型具有较高的精度，适用于研究输沙渠水沙运移特性。

2)根据水流特征变化可知，本文中4个方案的渠道内的水位、流速随上游河道流量的增加而增加，随渠底高程的降低而沿程下降。其中，渠道水流形态和流速方向基本一致，不同流量时流速变化最大的位置大致相同，流量为40、60 m3/s的变化趋势最为相似。除方案1受到泥沙淤积量的影响，水位降幅较大，其他3种方案的水位高程降低速率大致相同。

3)从泥沙淤积的纵向形态发展变化来看，方案1的泥沙淤积厚度从1.6 m至1.0 m逐层向后递减，方案2的泥沙沿程淤积较为均匀，淤积厚度为0.1～0.2 m，方案3、4的泥沙沿程淤积较少，渠道多存在冲刷现象，渠道内泥沙淤积厚度最大在0.1 m左右，表明流量增大后渠道内的泥沙显著减少。

4)通过对泥沙淤积总量的汇总及分析对比各方案的结果，方案3、4的累积淤积量变化不大，可以认为基本接近冲淤平衡状态，可以达到冲沙的目的，但方案4存在明显的冲刷渠底的现象，因此可选用流量为40 m3/s作为渠道冲沙的优选方案。