楼房仓在地震荷载作用下的易损性分析

谷智炜，柳春光

(1.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 建设工程学部水利工程学院 工程抗震研究所， 辽宁 大连 116024)

由于土地资源的短缺，改变现有平房仓的占地面积大的劣势，新的仓型研究是我们需要马上解决的问题。向立体式空间发展，或许是不错的选择[1-2]。随着国家倡导散装、散卸、散运、散存的“四散”储粮要求，散装粮食楼房仓符合现代粮食物流发展的需要[2]，开发楼房仓是十分迫切和必要的。

目前，用于储存粮食的主要结构有：筒仓以及平房仓。国内针对筒仓的地震作用研究较少[3]。国内外对平房仓及楼房仓的研究还存在大量空白。

近些年来，国内对楼房仓的结构选型有了较为合理的认知，张庆章等[4]对楼房仓建筑形式及结构方案进行了分析，认为平面形式为规则的矩形平面、井字楼盖框架结构是散装粮食楼房仓较好的结构形式。仇心义[5]以六层散装粮食楼房仓为例，经过探讨对比不同结构形式，认为应用框架结构井字楼盖较为合理，为此，本文将采用四跨的三层井字楼盖框架结构作为算例。

针对地震易损性方面的研究，增量动力分析法(IDA)可以用来对承受地震作用的结构进行概率性分析。Melania等[6]采用IDA对典型的低层钢筋混凝土框架进行了地震易损性。孙柏涛等[7]介绍了IDA方法的基本原理和操作步骤，选择符合要求的地震数据输入到分析软件中，通过分析得到的数据，绘制IDA曲线。

基于IDA的易损性分析结果可反映结构体系随地震动强度变化历经弹性、弹塑性至倒塌的全过程性能。因此对于散装粮食楼房仓的地震易损性分析略显重要。

1 基于IDA的地震易损性分析

1.1 地震波的选取及调幅

为了确保IDA分析的准确性，需要选取足够数量和满足要求的地震动记录。此外，考虑到地震波选取过程中的不确定性，参考文献[8]选取10条地震波即可精确评估结构抗震性能。从太平洋地震研究中心数据库选取了10条符合场地条件等要求的地震波。地震动具体信息见表1。

关于地震波的调幅，在选取了10条符合要求的地震波后，按照一定的调幅方法对地震波进行调幅。本文采用等步长法将选取的10条地震波进行归一化，取步长为0.1g，对归一化的地震进行调幅，形成PGA从0.1g到1.0g的地震波，然后输入结构进行时程分析。

1.2 IDA的指标选取及性能划分

IDA的基本参数为地震动强度参数(IM)和结构的工程需求参数(EDP)。《建筑抗震设计规范》[9](GB 50011—2010)中采用地面峰值加速度(PGA)作为动力时程分析的地震动强度参数。故本文选用PGA作为地震强度参数。针对结构的工程需求参数，考虑到结构最大层间位移角概念明确，能一定程度的反映结构损伤情况。参考文献[10]，最大层间位移角能够和建筑物结构的损伤程度建立起正确的关系。因此，本文将最大层间位移角作为结构的EDP来进行IDA分析。

参照我国《建筑地震破坏等级划分标准》[11]及文献[12]采用的“五水准”设防标准。相比“三水准”设防，“五水准”设防标准可以更好地控制结构在设计基准期内的地震经济损失。故本文将楼房仓框架结构划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌这五种性能水平，见表2。

1.3 地震易损性分析方法

由1.2小节可知，结构最大层间位移角与结构性能水平建立了定量的联系。因此，参考文献[13]给出的EDP与IM之间的关系满足公式：

EDP=αIMβ

(1)

式中：α、β为分布系数。

现取EDP的平均值D和PGA代入公式(1)，得到：

D=α(PGA)β

(2)

对式(2)两边取对数，有：

lnD=a+bln(PGA)

(3)

式中：a、b为线性回归系数，a=lnα，b=lnβ。

a、b可由地震峰值加速度(PGA)和结构最大层间位移角(θmax)进行线性拟合得到，从而得到系数α、β的值。

本文选用了回归分析法对该楼房仓框架结构进行IDA易损性分析。首先，将选取的10条地震波进行调幅，生成100组工况。经过ANSYS的时程分析法后，获得各个工况下结构最大层间位移角(θmax)，从而绘制IDA曲线。然后对已有的IDA曲线进行线性回归，求得线性回归系数。

参考文献[14]，结构的IDA分析结果可用如下数学表达式表示：

FR(a)=P(EDP>C/IM=a)

(4)

其中：FR表示地震易损性；P为结构失效概率；C为IM=a时的概率，a为一具体地震动强度值。

参考文献[15]，可根据式(5)，得到结构各极限状态的超越概率曲线。

(5)

式中：θi为各个极限状态所对应的层间位移角限值；μlnθ|PGA为最大层间位移角的对数均值；σlnθ|PGA为对数标准差。

2 算 例

2.1 楼房仓有限元模型的建立

本文以某粮油工业公司散装粮食仓为算例，建筑场地类别为Ⅱ类，地区抗震设防烈度为8度，设计基本加速度为0.3g，设计地震分组为第2组。工程结构形式为三层井字梁框架结构。结构层高分别为：一层11 m、二层和三层8 m，总高为27 m。平面尺寸为28 m×30 m，横向和竖向各4跨。结构立面及平面如图1、图2所示。满仓堆粮线分别为：一层8 m、二层和三层5 m。空仓梁柱和满仓粮食的ANSYS模型如图3、图4所示。

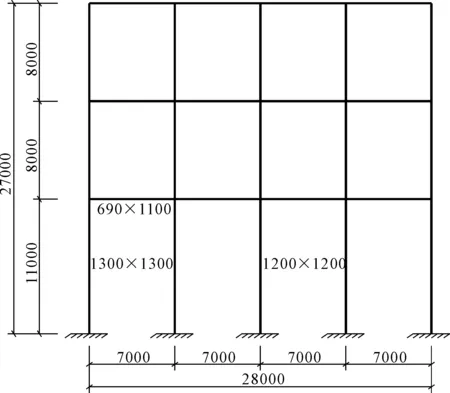
图1 楼房仓立面图(单位:mm)

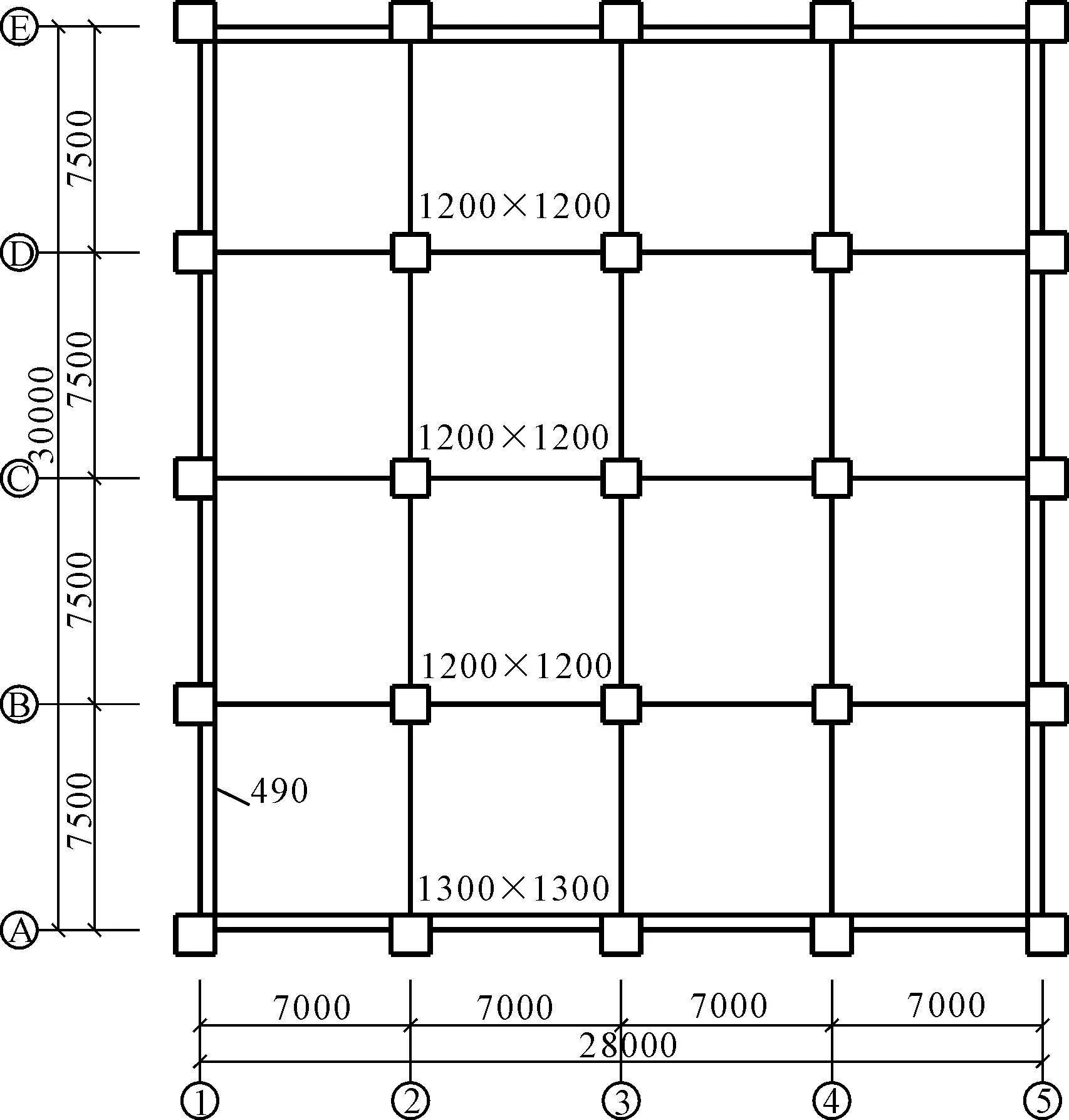
图2 楼房仓平面图(单位:mm)

梁柱混凝土的强度设计等级为C30，结构的梁柱单元采用Beam189单元，结构的墙壁及楼板采用壳体单元Shell181，仓壁厚490 mm，楼板厚200 mm。混凝土的本构关系模型为Rüsch提出的理想弹塑性本构模型[16]，这也是我国《混凝土结构设计规范》[17](GB 50010—2010)采用的应力-应变曲线。其应力-应变曲线上升段和直线段的表达式见式(6)和式(7)：

(6)

ε0≤ε≤εcu，σ=fc

(7)

图3 梁柱有限元模型

图4 整体模型有限元模型

混凝土的本构曲线见图5。

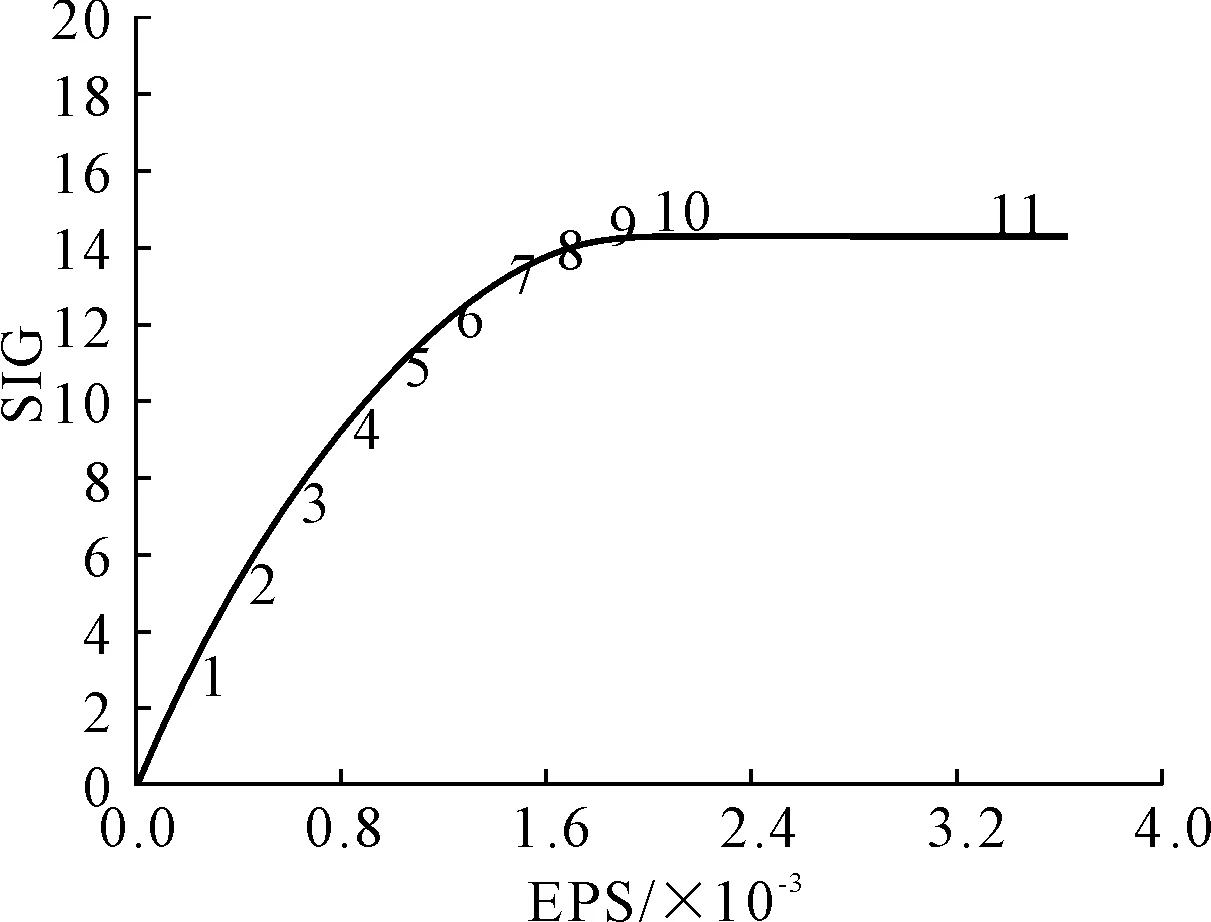
图5 混凝土本构曲线

建立好三层的框架结构后，开始针对粮食散料进行研究。散料采用可进行塑性、蠕动、大变形等分析的实体单元Solid45，并且散料服从Drucker-Prager屈服准则[18-21]，DP模型的屈服面表达式为：

F=αI1+J2-σ

(8)

式中：I1为第一应力不变量；J2为第二偏应力不变量；α、σ为材料参数。

采用非关联流动法则时：

(9)

式中：φ为散料有效内摩擦角；c为材料黏性系数。

DP屈服准则的三个材料参数：黏结力c、膨胀角ψ和材料内摩擦角φ。参考文献[22]，材料参数的数值要基于一定的试验数据基础上，本文粮食散料的各项参数见表3。粮食散料的单元模型如图6所示。

表3 散料各参数设置

图6 散料单元模型

2.2 散料与仓壁的接触模拟

为传递粮食散料单元与楼房仓结构之间的相互作用力，需要对两者之间加入接触单元。这也就涉及到接触分析。

接触分析是典型的状态非线性问题。它是一种高度非线性分析，因此在进行有限元分析过程中，接触单元的选取及接触单元的数据定义显得至关重要。否则将会导致地震时程分析计算不收敛，得到的结果也将偏离现实。

对于接触方式，共有三种模拟接触的方法，分别为：面面接触、点面接触、点点接触。本文建立的粮食散料单元采用Solid45实体单元，与之接触的是结构仓壁、楼板的Shell181壳体单元，这属于面面碰撞作用。因此在进行模拟时，本文选择接触方式为面面接触。

对于接触单元[23-24]，选择Conta173作为接触单元，选择Targe170为目标单元。将接触单元Conta173建立在散料的Solid45单元表面上，目标单元Targe170建立在仓壁的Shell181单元表面。为确保结果的准确性，在划分单元时确保壳体单元和实体单元对应，使得接触对正确识别，利于计算收敛。最终建立完成后的接触单元见图7。

图7 接触单元模型

对于接触类型，主要有两种：(1) 刚柔接触，即一个材料的表面相对于另一个与之接触的材料表面是完全刚性或刚度大很多，可采用刚柔接触；(2) 柔柔接触，即2种材料表面刚度相近，共同变形。本文考虑到散料与钢筋混凝土材料刚性相差较大，因此选择刚柔接触。

对于接触算法而言，仓壁与粮食散料之间算法选择ANSYS默认的增广拉格朗日法。该法主要适用于面面接触、点点接触。在楼板与粮食散料底部的接触算法为多点约束法(MPC)。主要作用是通过施加约束方程把接触面的位移联系在一起，不涉及接触刚度，适用于不能法向运动可以切向运动的情况。接触分析时，参数的设置很重要，接触刚度系数应尽可能大以减小接触单元的穿透值。故本文将接触刚度(FKN)取为1.0。

接触单元及接触算法的建立，是粮食与结构之间相互作用的重要关键，也是结构在地震时程分析时收敛的关键。因此有必要对其进行一定的测验，以确保建模的准确性。可以通过对三层满仓结构进行重力分析以获取散料与仓壁之间的侧压力及竖向摩擦力，并将其与我国《粮食平房仓设计规范》[25](GB 50320—2014)进行对比。如图8所示，通过ANSYS建立的模型，散料的侧压力和竖向摩擦力整体趋势和数值同规范相近，证明模型建立的正确性。由图8可知，法向压力和竖向摩擦力先随着深度的增加而增大，但在分别距仓底为2 m和4 m处开始随深度的增加而减小，之后减小到仓底处的零。由参考文献[26-27]可知：(1) 竖向摩擦力在仓底时为0，是由于粮食单元与仓壁单元没有相对位移；(2) 由于建模时对散料和结构底部采用了相对保守的位移完全约束，故侧压力在2 m处存在弯折点。

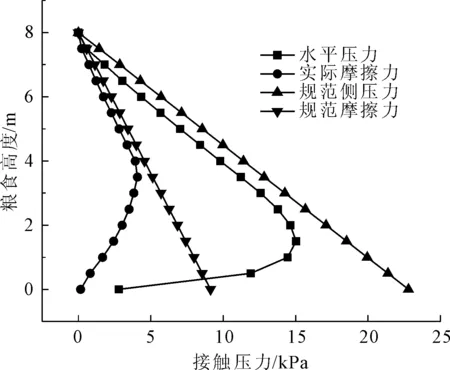
图8 散料接触压力

2.3 易损性分析

由1.2及1.3小节可知，通过ANSYS对结构的x方向施加100条之前调幅的地震动记录，分别进行时程分析。得到每条地震波不同峰值加速度(PGA)下的结构最大层间位移角(θmax)，绘制出震峰值加速度与最大层间位移角与的关系曲线，见图9。由图9可知：(1) IDA曲线存在着离散性，绝大多数的IDA曲线斜率随着PGA的增大逐渐降低；(2) 随着PGA的增大，最大层间位移角逐渐达到破坏、倒塌的限值。这表明楼房仓结构在粮食散料与地震的双重作用下，结构逐步从线弹性到弹塑性阶段的转变。少部分IDA曲线呈现曲折上升、斜率近乎不变的现象，可能与对应的地震动波动的频率有关。此外对比文献[28]中同样三层结构的IDA曲线，装有满仓粮食的楼房仓IDA曲线在前段的最大层间位移角较小、斜率较大，能够看出此时结构整体的抗震性能较好。由此说明满仓粮食散料在一定强度地震作用下对结构有缓冲保护作用，使得整体结构的刚度较大。但超过这一地震动强度，结构的层间位移角就会急剧增大、快速破坏，IDA曲线中后段的斜率也逐渐变小。满仓粮食对于进入塑性阶段的楼房仓结构是不友好的，其加剧了楼房仓破坏。

根据1.3小节的地震易损性分析方法，在IDA分析的基础上，对地震峰值加速度(PGA)和结构最大层间位移角(θmax)分别取对数并进行线性回归分析，见图10。通过公式(5)，可得到楼房仓结构的超越概率，由此绘制出易损性概率曲线，见图11。由图11可知，在同一地震强度下，结构性能状态从正常使用到防止倒塌的超越概率依次减小。

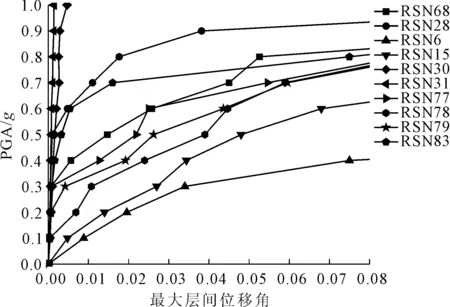
图9 IDA曲线族

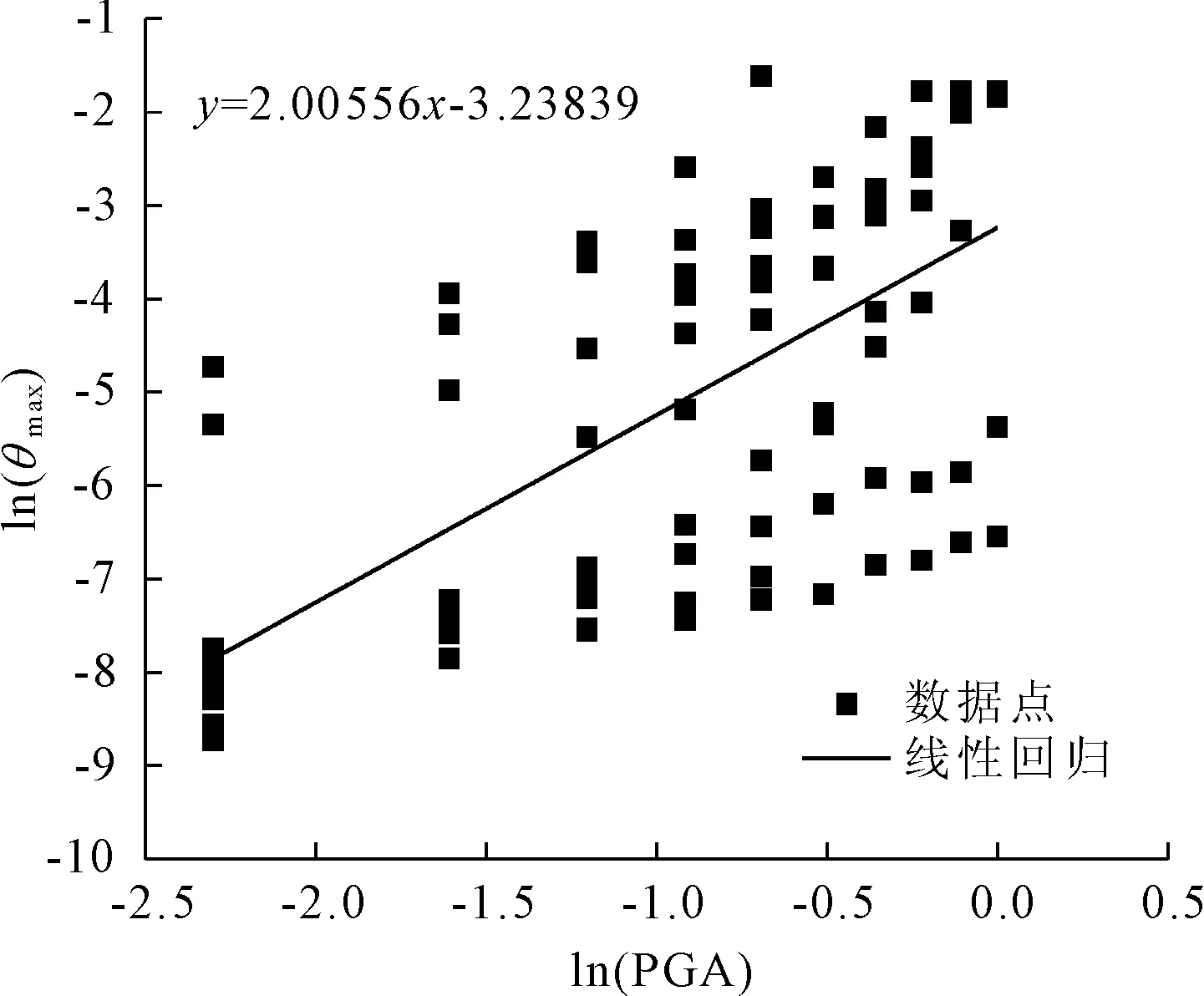
图10 概率需求分析

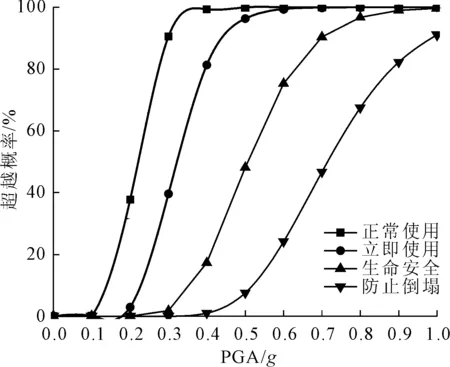
图11 易损性概率曲线

根据我国《抗规》[9]规定的三水准设防要求，在给定的算例下，多遇、罕遇地震对应的地震加速度时程的最大值分别是110 cm/s2和510 cm/s2。根据已得到的易损性概率曲线得出不同地震水准下结构各极限状态的破坏概率，见表4。由表4可知，满仓粮食楼房仓在多遇地震作用下保持基本完好的概率为97.4%，发生轻微破坏的概率较小，无中等破坏及以上的倒塌现象。主要原因可能是满仓粮食使得结构的整体刚性加大，对地震作用产生了一定的抑制效果，这使得结构偏于安全，满足“小震不坏”的要求。在规定的8度设防地震作用下，楼房仓发生轻微破坏和中等破坏概率大大增加，分别达到了50.94%和37.83%，无倒塌现象，满足规范要求的“结构经一般性修理仍可继续使用”，即“中震可修”。在规定的8度罕遇地震作用下，楼房仓以中等破坏及严重破坏为主，为别占45.22%、42.75%，发生倒塌的概率为8.73%。根据报告[29]中提到的在最大地震动作用下，对于某一结构其平均倒塌概率应不大于10%。因此在罕遇地震下楼房仓仍具有一定的抗倒塌储备。故该楼房仓框架结构在粮食满仓的情况下能够基本满足抗震性能的要求。

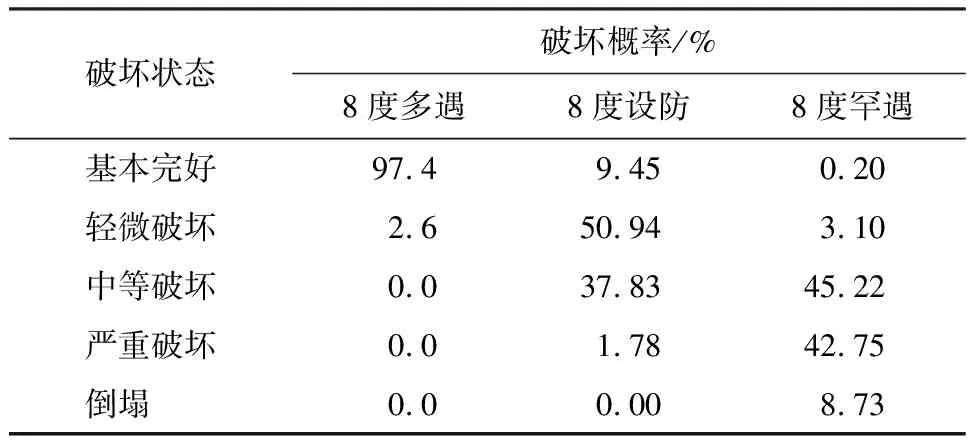
表4 不同地震水准下结构各极限状态破坏概率

3 结 论

本文从性能设计的角度来考虑，以满仓粮食下的楼房仓框架结构为算例进行了基于IDA方法的地震易损性分析。得到以下四点结论：

(1) 考虑粮食作用，通过ANSYS对楼房仓进行地震时程分析，得到楼房仓结构在不同地震动强度下的最大层间位移角，由此得到楼房仓的IDA曲线。这可为钢筋混凝土结构楼房仓的易损性分析提供参考。

(2) 根据IDA曲线，得到结构“五水准”设防标准下各极限状态的超越概率曲线，并进一步算得楼房仓在不同地震水准下的各极限状态破坏概率，由此可对满仓粮食下楼房仓结构的性能水平进行定量的分析。

(3) 由IDA曲线可知，在一定地震强度下，粮食的存在有利于提高楼房仓的抗震性能。此时的粮食运动作用不足与对结构产生相对且颠覆的改变，但随着地震强度的增大，粮食的重力和水平运动作用对结构来说都是不利的，并会导致楼房仓结构迅速进入塑性，导致其破坏概率和破坏程度剧增，这也是IDA曲线后半段斜率变低的主要原因。

(4) 满仓粮食楼房仓结构在8度多遇地震和设防地震作用下，基本满足了《抗规》要求的“小震不坏、中震可修”的基本设防要求，并且结构在设防地震作用下，大概率进入塑性阶段，表现出结构具有一定的延性。在8度罕遇地震和粮食的双重作用下，结构有8.73%的概率接近倒塌。考虑到结构自身的弹塑性性能，认为结构在“大震”下仍具有一定的抗倒塌储备。因此满仓粮食下的楼房仓结构具有足够的安全储备。