基于小波包的无绝缘轨道电路补偿电容故障特征分析

洪玲，武晓春

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

随着铁路的发展，无绝缘轨道电路因为具有良好的抗干扰能力和较高的线路寿命而被广泛应用。其中ZPW-2000A无绝缘轨道电路因其较高的安全性能和较好的传输性能，从2003年起，在铁路全路全面应用[1]。因此，本文以ZPW-2000A为代表对无绝缘轨道电路进行分析。在ZPW-2000A中，采用在钢轨上加装补偿电容方式提高轨道电路传输长度。铁路现场中，补偿电容故障主要表现为断线故障和容值下降，据孟景辉等[2]研究发现，这2种故障约占全年补偿电容故障总数的98%。补偿电容故障有可能导致轨道电路出现“红光带”和机车信号出现“掉码”现象。而针对补偿电容故障，目前铁路现场广泛采用专用检测车定期检测的方法，该方法可能导致补偿电容故障不能被及时发现，故很难采取有效的预防措施[3]。因此，目前国内外学者基于轨道电路的分路电流，对补偿电容进行研究。ZHAO等[4]基于轨道电路仿真数据计算并分析出不同位置补偿电容结构的重要性，为现场工作人员确定各补偿电容维护优先级提供依据；ZHANG等[5−6]分别基于模拟退火算法和模糊定性趋势，实现了补偿电容的故障诊断；DONG等[7−8]分别基于动态时间规划和TCR(Track Circuit Reader)监测数据，实现了补偿电容的故障诊断和容值估计。目前铁路现场希望从补偿电容的故障诊断、状态检测等多个角度出发，以实现对补偿电容的状态监测和故障预测，满足补偿电容从“故障修”到“状态修”的转变。因此，本文采用小波包分析补偿电容的故障特征，从而为补偿电容状态监测和故障预测提供数据支持。在ZPW-2000A无绝缘轨道电路上，由于补偿电容的作用，轨面上的移频信号具有非线性特性。而在进行非线性信号分析时，学者一般采用时频分析方法，其中威格纳时频分析、经验模态分解、局部均值分解、小波分析、小波包分析等方法更是因其在非线性信号分析上具有良好效果而得到广泛应用[9]。威格纳时频分析具有很好的分辨率，但其存在交叉干扰项；经验模态分解自适应能力强，但存在端点效应和模态混叠；局部均值分解信噪比高，但由于存在瞬时频率函数极值，导致扰动时间定位不准确；小波分析具有良好的时频局部化功能，但在高频部分的时频分辨率差；而小波包可更详细地划分信号的高频部分，提高了时频分辨率[10−11]。因此，本文采用小波包对轨道电路补偿电容全部正常、发生断线故障和容值下降故障这3种情况的分路电流幅值包络曲线进行分解和重构，并将补偿电容正常时对应的重构后小波包系数曲线与其他2种情况对应的重构后小波包系数曲线进行对比分析，得到故障特征明显的频段；计算选出频段对应补偿电容处瞬时能量，通过将补偿电容全部正常时各补偿电容对应的瞬时能量与其他2种情况下各补偿电容对应的瞬时能量进行对比分析，从而得到补偿电容发生断线故障和容值下降时的故障特征。

1 ZPW-2000A无绝缘轨道电路建模

1.1 轨道电路工作原理

ZPW-2000A无绝缘轨道电路由发送端设备、补偿电容以及接收端设备连接而成，其系统结构可分为室外设备和室内设备两部分，其中室外设备有钢轨、补偿电容、双体防护盒、实际电缆等；室内设备有发送器、防雷模拟网络盘、衰耗冗余控制器、接收器和通信接口板等。ZPW-2000A系统结构图如图1所示。

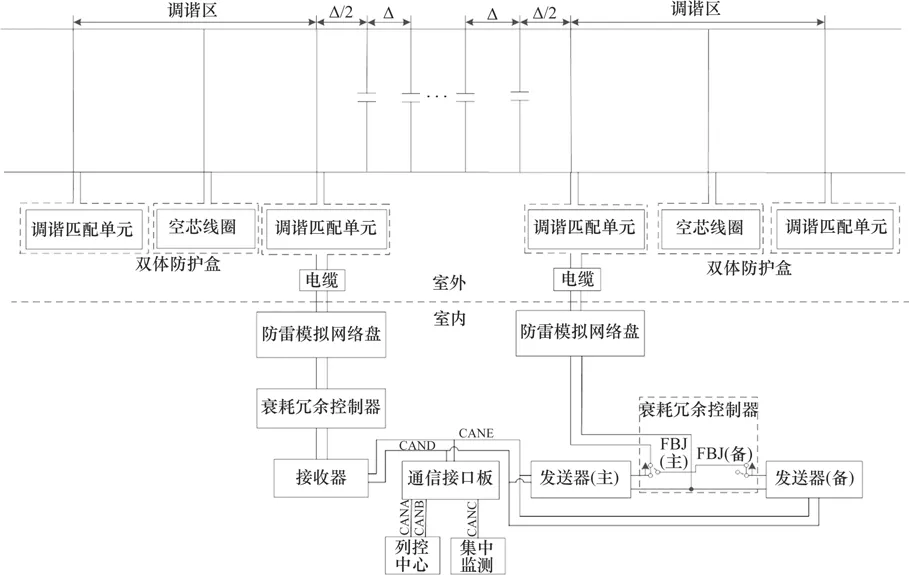
图1 ZPW-2000A系统结构Fig.1 ZPW-2000A system structure

轨道电路正常运行时存在调整态和分路态2种状态。调整态时发送器发出移频信号，经轨道电路传输到达接收端，最后接收端接收信号并驱动相应的轨道电路继电器动作；分路态时，由于列车轮对的短路作用，使得轨道电路大部分电流经列车轮对又重新回到发送端，只有少部分残压到达接收端，导致接收端接收信号小于其规定的阈值，从而使轨道继电器落下，轨道电路处于“有车占用”状态[12]。

1.2 调整态轨道电路建模

在ZPW-2000A系统中，可把除发送器和接收器外的其它设备用等效四端网络表示，将这些四端网络与发送器和接收器级联起来，即可实现轨道电路模型的建立[13−15]。故可得ZPW-2000A无绝缘轨道电路调整态模型如图2所示。

图2中，NSSR和NRSR分别为发送端和接收端衰耗冗余控制器的等效四端网络；NSDL和NRDL分别为发送端和接收端实际电缆与防雷模拟网络盘的等效四端网络；NSTP和NRTP分别为发送端和接收端调谐匹配单元的等效四端网络；NTZG为调整态时轨道线路的等效四端网络；US和UR分别为发送端和接收端的发送电平和接收电平；IS和IR分别为发送端和接收端的发送电流和接收电流。

图2 轨道电路调整态模型Fig.2 Track circuit adjustment state model

1.3 分路态轨道电路建模

当列车占用该轨道电路时，列车第1轮对将轨道电路分路，因此列车第1轮对相当于分路电阻Rf，轨道电路分路过程就是分路电阻Rf从接收端到发送端依次分路各补偿电容的过程[16]。设置NFLG为分路态发送端调谐区到列车第1轮对前方接收线圈的轨道线路等效四端网络；N1.5为列车接收线圈到分路点的等效四端网络，其中列车接收线圈到Rf的距离为1.5 m；ZFLJS为分路点到接收端的阻抗，If和IFLJS分别为流过Rf和ZFLJS的电流。故可得ZPW-2000A无绝缘轨道电路分路态模型如图3所示。

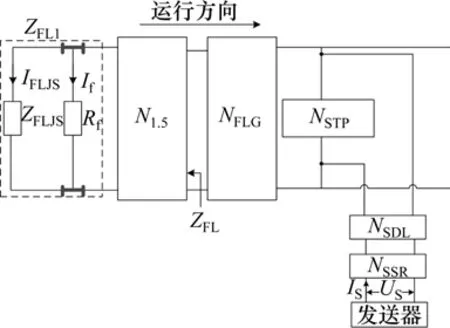
图3 轨道电路分路态模型Fig.3 Shunting state model of track circuit

图3中，ZFL1为Rf到接收端的视入阻抗，由于ZFLJS远大于Rf，故ZFL1表达式如下：

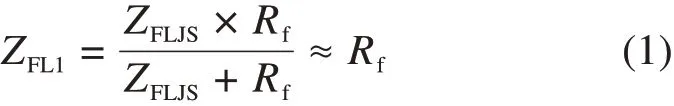
ZFL为分路态时列车接收线圈到接收端的视入阻抗，其表达式如下：

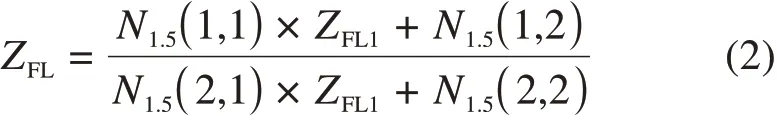
假设NFLGZ为分路态轨道电路从发送端到列车接收线圈的总体等效四端网络，则其表达式如下：

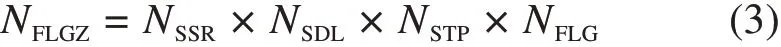
综上可得分路电流幅值AFL表达式如下：

2 小波包分析

在ZPW-2000A无绝缘轨道电路中，由于补偿电容的作用，根据分路态轨道电路建模型分析得到的分路电流幅值曲线具有非线性特性。因此，可采用小波包分解处理分路电流幅值曲线；同时，为了防止能量畸变，需要对分解后的信号进行小波包重构；最后，因为小波包能量中一般会包含大量原始信号，因此可通过对重构后信号计算小波包能量，从而通过分析小波包能量得到补偿电容故障特征。

2.1 小波包分解和重构

小波分解可用于突变信号和有孤立奇异点函数的处理，通过小波分解能够在时域和频域内表征原始信号的局部特征。但是，小波分解对高频部分分辨率低。而小波包分解在小波分解的基础上，对信号高频部分进行进一步分解，克服了小波分辨率低的特点，提供了更全面的信号分析[17]。小波包分解树如图4所示，其中“S”为低频小波包信号，“d”为高频小波包信号。

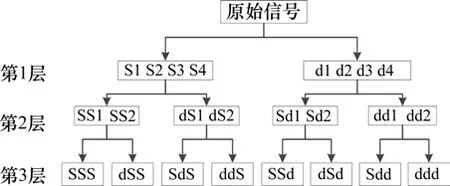
图4 小波包分解树Fig.4 Wavelet packet decomposition tree

小波包分解过程中，随着分解层数的增加，小波包系数的长度会变短，而当小波包系数的长度过短时可能会导致其能量发生畸变。因此，在对原始信号进行小波包分解后，还需进行小波包重构。小波包分解和重构的计算表达式如式(5)和式(6)所示[18]。

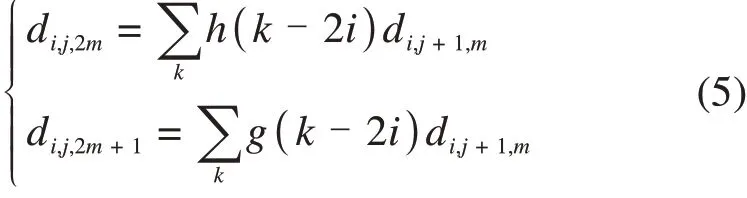
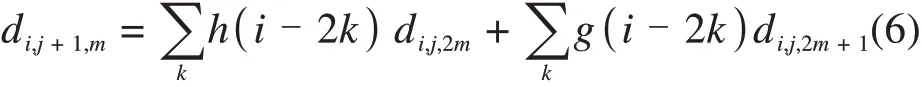
式中：di,j,m表示第j层第m个节点的第i个小波包系数；h(k)和g(k)分别是低通和高通滤波器系数。

2.2 小波包能量谱

小波包能量包含了丰富的故障知识，它在某一特定分量上的波动对应于某一特定故障的发生，因此，可从小波包能量中得到故障特征。小波包能量表达式如式(7)所示[19]。

式中：m=0，1，2，…，2j−1。

2.3 小波包故障特征分析

利用小波包可实现非线性信号的分析，小波包分析将原始信号分解为多个时频带，此时可通过观察特定频带内的时变信号特征对原始信号进行分析。同时，小波包能量中包含大量的故障信息，通过对特定频带计算其小波包能量并分析，可得到故障特征。因此，本文基于轨道电路分路态模型仿真得到补偿电容不同故障类型下的归一化分路电流幅值包络曲线，接着采用小波包对这些归一化分路电流幅值包络曲线进行分解和重构，并通过对这些重构后的小波包系数图进行对比分析，得到故障特征明显的小波包频带；最后，计算这些频带在补偿电容处的瞬时能量并进行对比分析，得到补偿电容的故障特征。

3 仿真分析

3.1 分路电流幅值包络曲线仿真

基于无绝缘轨道电路模型，分别对补偿电容全部正常，C5容值下降30%以及C5容值下降60%，C5断线以及C5和C7同时断线这些情况进行仿真，得到归一化分路电流幅值包络AFL曲线如图5所示。仿真条件如下：主轨道电路长度为960 m，所在载频为2600-1，分路电阻为0.15Ω，则根据无绝缘轨道电路电气参数[20]可得，补偿电容个数为12个，发送器发送1级电平，功出电压为170 V。

由图5可知，补偿电容容值发生断线故障或容值下降时，轨道电路对应的归一化AFL曲线具有以下规律：

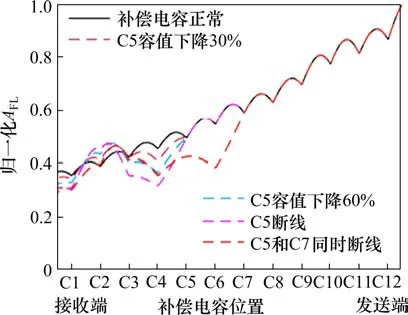
图5 补偿电容不同故障类型归一化A FL仿真曲线Fig.5 Normalized A FL simulation curves for different fault types of compensation capacitor

1)当补偿电容发生故障时，主要影响故障电容到接收端方向的归一化分路电流幅值波动情况，而几乎不影响故障电容到发送端方向的归一化分路电流幅值波动情况。

2)轨道电路补偿电容全部正常时，归一化分路电流幅值包络曲线从发送端到接收端呈现规律性分布，且在补偿电容处存在极小值点。

3)当C5发生容值下降故障时，由C3到C5处归一化分路电流幅值曲线可以看出，补偿电容容值变化会破坏其原有的规律性分布，且C3到C5处归一化分路电流幅值曲线随着补偿电容容值下降在不断下移。

4)当补偿电容发生断线故障时，归一化分路电流幅值曲线在故障电容处的极小值点消失。

3.2 小波包分解

采用小波包对轨道电路补偿电容全部正常、C5发生断线故障以及C5和C7同时发生断线故障、C5容值下降30%以及C5容值下降60%这些情况对应的归一化AFL曲线进行分解和重构，得到重构后的小波包系数曲线如图6所示。其中，图6(b)中红线表示C5发生断线故障时对应的小波包系数曲线，绿线表示C5和C7同时发生断线故障时对应的小波包系数曲线；图6(c)中红线表示C5容值下降30%时对应的小波包系数曲线，绿线表示C5容值下降60%时对应小波包系数曲线。

图6中，横坐标表示补偿电容位置，纵坐标s30～s37表示各频段的小波包系数值，即将原始信号经过分解和重构后，不同频段对应的归一化分路电流幅值。

续上图

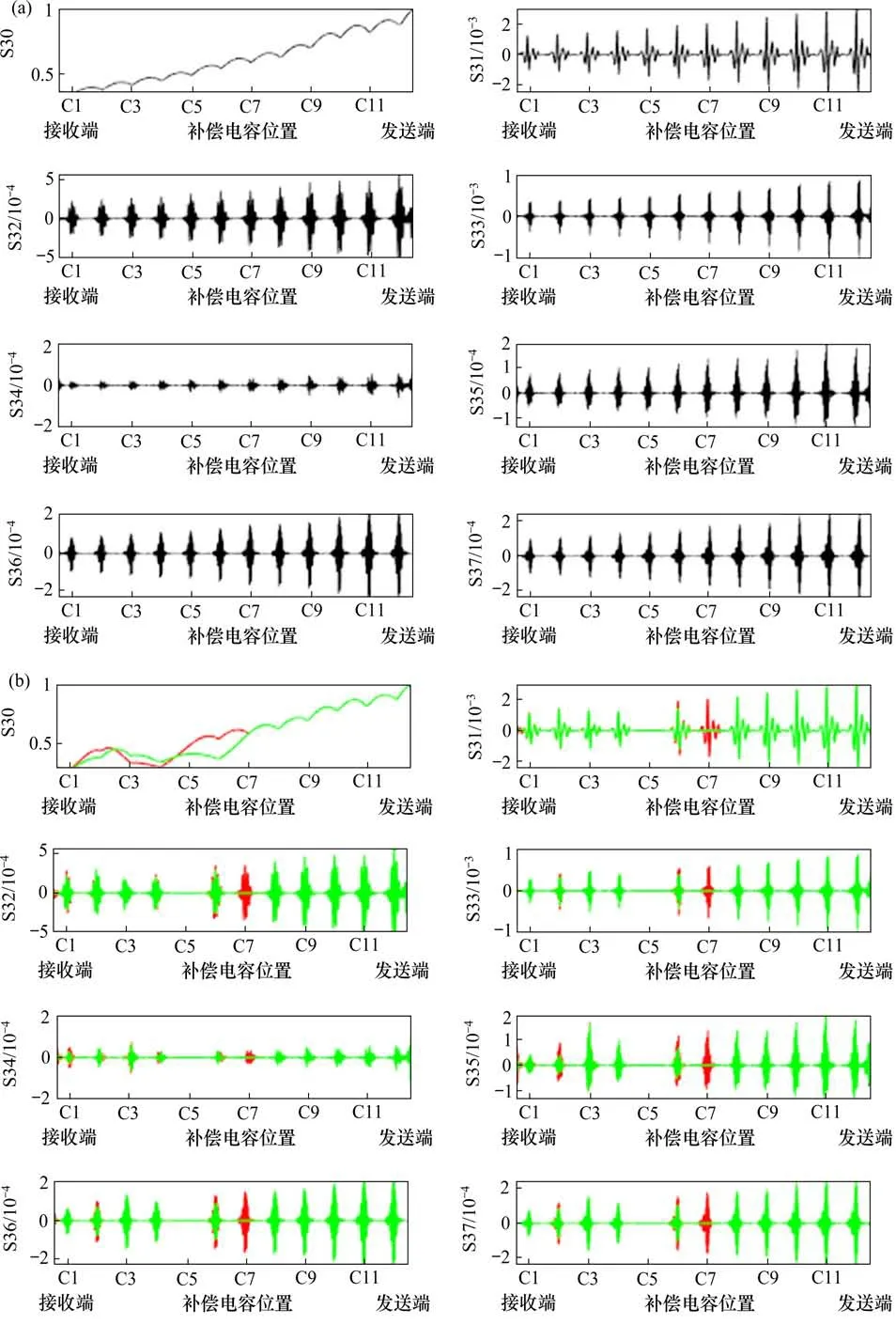
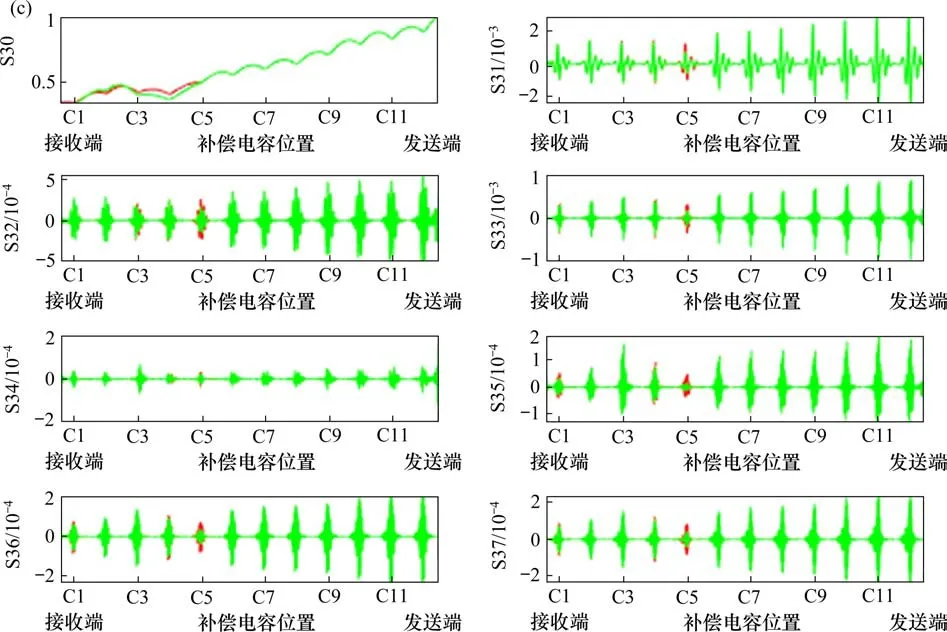
图6 补偿电容全部正常和补偿电容不同故障类型时的小波包系数曲线Fig.6 Wavelet packet coefficient curve when all the compensation capacitors are normal and the compensation capacitors have different fault types

由图6(a)可知，补偿电容全部正常时，各补偿电容处对应的小波包系数有明显的幅值，且该幅值明显大于0。

将图6(a)和6(b)进行对比分析可知，当补偿电容发生断线故障时，在故障电容处第3层后7个频段小波包系数接近为0。

将图6(a)和6(c)对比可知，当C5发生容值下降故障时，第3层后7个频段小波包系数图中，随着C5容值下降，C5处对应的小波包系数在不断地向0靠拢。

因此，基于上述变化特征，本文选取后7个频段进行故障特征分析。

3.3 故障特征分析

计算出轨道电路补偿电容全部正常、C5发生断线故障以及C5和C7同时发生断线故障、C5容值下降30%以及C5容值下降60%时后7个频段对应补偿电容处的瞬时能量，并将后7个频段对应相同补偿电容处的瞬时能量相加，得到补偿电容全部正常与补偿电容发生断线故障和容值下降时不同位置补偿电容的瞬时能量对比图如图7所示。

图7(a)中，当轨道电路补偿电容全部正常时，从发送端到接收端，不同位置补偿电容处的瞬时能量呈现衰减趋势；而当C5发生断线故障时，C5对应的瞬时能量接近为0；当C5和C7同时发生断线故障时，C5和C7处对应的瞬时能量也是接近为0。对C1至C12分别试验，发现也是具有相同规律：发生断线故障的补偿电容处对应的瞬时能量接近为0。

由图7(b)可以看出，当轨道电路正常时，从接收端到发送端，各补偿电容对应的瞬时能量呈现上升趋势，其中距离发送端越近的补偿电容位置对应的瞬时能量越大；而当C5发生容值下降故障时，C5对应的瞬时能量降低，且其瞬时能量小于C4和C6对应的瞬时能量。通过对C1到C12发生不同程度容值下降时的瞬时能量进行分析可知：对于C12，当其容值下降8%及以上时，具有以下特性，即故障电容对应的瞬时能量由正常时大于C11对应的瞬时能量变为小于其瞬时能量；对于C2到C11，当其容值下降10%及以上时，均具有以下特性，即故障电容对应的瞬时能量既小于前一个补偿电容对应的瞬时能量，又小于后一个补偿电容的瞬时能量；而对于C1，当其余补偿电容全部正常时，将C1对应的瞬时能量与其正常时的能量进行对比分析知，当其小于正常时C1的瞬时能量时，即C1发生容值下降故障。

图7 补偿电容全部正常与不同故障类型时的瞬时能量对比Fig.7 Comparison of instantaneousenergy when all the compensation capacitors are normal and the compensation capacitors have different fault types

将图7(b)中C5发生不同程度容值下降时对应的瞬时能量值提取出来，得到结果如表1所示。

表1 瞬时能量比较Table 1 Comparison of instantaneous energy

根据表1，C5容值下降30%与补偿电容全部正常时C5对应的瞬时能量比值的方根为0.683，而1与0.683差值的百分比等于31.7%；C5容值下降60%与补偿电容全部正常时C5对应的瞬时能量比值的方根为0.381，而1与0.381差值的百分比等于61.9%。由此可看出，C5发生容值下降故障时，其故障对应的瞬时能量与补偿电容全部正常时对应的瞬时能量比值的方根与1的差值的百分比大致相当于C5容值下降百分比，故可利用上述规律分析其他补偿电容发生不同程度容值下降时故障电容对应的瞬时能量。

3.4 实测曲线验证

图8实线为某铁路局于2019年9月9日进行定期巡检时，补偿电容全部正常情况对应的某个轨道电路归一化分路电流AFL的实测曲线。

图8 正常情况下的仿真曲线与实测曲线对比Fig.8 Comparison of simulation curve and measured curve under normal condition

根据本文方法，对图8中实测曲线进行小波包分解和重构并提取补偿电容处对应的瞬时能量，得到补偿电容C1到C7处对应的瞬时能量分别为2.0520×10−6，2.102 9×10−6，2.199 3×10−6，2.321 1×10−6，2.417 7×10−6，2.633 1×10−6，3.004 0×10−6。通过对瞬时能量分析可知，从接收端到发送端，各补偿电容处对应的瞬时能量呈现上升趋势，因此可判断该轨道电路补偿电容全部正常，这与实际检测结果一致，因此可验证本文算法的可行性。

同样的，基于分路态轨道电路模型仿真得到轨道电路补偿电容全部正常时的归一化分路电流AFL，仿真曲线如图8虚线所示。由图8仿真曲线与实测曲线对比可知，本文基于分路态轨道电路模型仿真得到的归一化分路电流幅值曲线与实测曲线大致相似，进而也验证了本文模型的可行性。但是图8中仿真曲线与实测曲线并不完全重合，而是存在一定的误差，这是因为轨道电路运行时易受到如谐波、雷击等外界因素的干扰，因此在建模过程中，还需要考虑外界干扰因素，从而减少误差，提高准确度。

4 结论

1)当补偿电容全部正常时，分路电流幅值曲线呈现规律性分布且在补偿电容处存在极小值点；当补偿电容发生容值下降时，会破坏其原有规律性，故障电容到接收端对应的分路电流幅值曲线随着容值下降在不断下移；当补偿电容发生断线故障时，分路电流幅值曲线在故障电容处的极小值点消失。

2)通过对补偿电容全部正常、发生断线故障和容值下降故障时各补偿电容对应的小波包瞬时能量分析知，补偿电容全部正常时，从发送端到接收端各补偿电容对应的瞬时能量在逐渐变小；当补偿电容发生断线故障时，故障电容对应的瞬时能量几乎为0；当补偿电容发生容值下降故障时，故障电容对应的瞬时能量小于前后2个补偿电容对应的瞬时能量。因此，基于小波包瞬时能量可实现补偿电容断线故障和容值下降时的故障特征分析。

3)当补偿电容发生容值下降故障时，计算故障电容对应的瞬时能量与补偿电容全部正常时对应的瞬时能量比值的方根，而1与该方根差值的百分比大致相当于该故障电容容值下降百分比。因此，基于上述计算方法可大致判断该故障电容的容值下降百分比。