远距离高阻抗送出发电机失磁过程仿真及保护分析

张兵海苏 灿陈 鹏王心蕊焦玉刚

(1.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2.国网刘家峡水电厂,甘肃 临夏 731600;3.陕西德源府谷能源有限公司,陕西 榆林 719400)

0 引言

发电机与电网连接后,汽轮机(或水轮机等)继续调升转速的能量转换为送出有功功率,继续调升励磁电流的能量则转换为送出无功功率。有功、无功功率送出的量值与机组和电网参数相关联,在机组参数(含升压变压器)不变的情况下,送出系统的阻抗、电压包括输电线路、变电站设备、负荷阻抗等参数对功率的送出关系密切。当送出系统阻抗大到一定程度时,尤其是经过超长输电线路连接到超高压或特高压电网的发电机组,一般认为可能存在出力受限的问题。与出力受限相对应,发电机失去励磁时,一般认为按照DL/T 684—2012《大型发电机变压器继电保护整定计算导则》(简称“整定导则”)[1]取异步阻抗圆(简称“异步圆”)整定的发电机失磁保护可能存在无法动作的问题。

本文通过PSCAD 仿真软件,对这种接于超高压或特高压的远距离高阻抗输电系统,发电机失磁过程进行仿真,对失磁后发电机机端阻抗轨迹和失磁保护整定原则进行了分析,提出了适用于送出系统超高阻抗时的失磁保护异步圆整定原则。

1 发电机失磁过程分析

1.1 发电机并网状态功率

发电机与电网连接后的功率理论表达式,见式(1)和式(2)。

式中:P为发电机并网后输出的有功功率;Q为发电机并网后输出的无功功率;E0为发电机内电势;Us为系统电压;δ为功角,即发电机内电势与系统电压之间的角度差;XdΣ为整体直轴感抗,包含发电机电抗、升压变压器电抗、电网电抗;XqΣ为整体交轴电抗,对于隐极机,认为XdΣ=XqΣ,式(1)简化为式(2)。

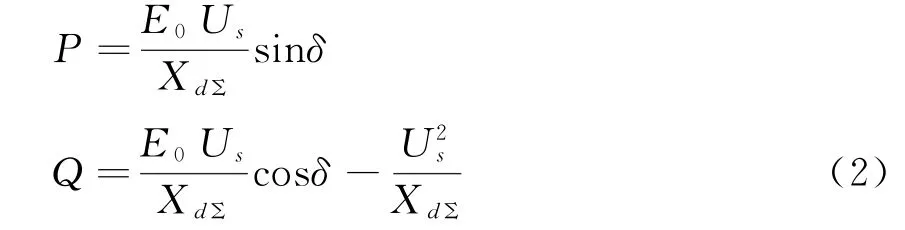
由式(1)或式(2)可以看出,当XdΣ大到一定程度时,即机组与系统联系较弱时,发电机的出力会受限。同理,发电机失磁时,发电机的进相功率也将受影响,当失磁保护整定为阻抗圆时,面临异步圆和静稳圆的选择问题[2],整定不当可能引起相应故障时的保护拒动。

1.2 发电机失磁后电量参数滑行轨迹

发电机失磁故障产生原因有多种,包括励磁调节器故障、整流功率元件故障、励磁回路短路和开路、转子绕组短路和开路等,不同的故障部位最终对应的故障现象均为转子电压和/或转子电流的消失。

以发电机转子绕组完全短路为例,当转子绕组突然短路后,转子电压Efd瞬降为零,但转子电流Ifd有一个衰减的过程,衰减时间常数为Lrotor/Rrotor,在惯性时间Tj之前机械转矩即汽(水)轮机动力没有变化,这样发电机内电势与系统电压间功角δ逐渐增大。随着δ增大,使cosδ变小,当后发电机机端的阻抗轨迹由第1象限向第4象限滑过R轴,即X过零点;当δ=90°时发电机送出的有功功率为最大值,即机端阻抗的R值最大;当δ继续增大,因为sinδ变小、cosδ增大,发电机送出的有功则开始降低、无功反方向开始数值增大;δ大于180°后,有功反向数值开始增大,无功仍为反向数值开始变小,发电机进行失步状态。

一般正常运行功角δ0<45°,失磁后从δ0到90°区间,机端阻抗沿等有功圆滑行,在90°到180°区间,Ifd衰变趋于平缓,机端测量阻抗的X值近似恒值,这个过程X≈X″d,即惯性时间Tj之后功角超过180°,机组变为异步运行。

1.3 发电机阻抗圆原理失磁保护行为分析

发电机失磁后阻抗轨迹在从第1象限沿等有功圆滑到第4象限异步运行后,应进入失磁保护整定的静稳或异步阻抗圆,保护动作。发电机失磁保护阻抗圆见图1。

图1 发电机失磁保护阻抗圆

图1中,圆1为静稳阻抗圆(简称“静稳圆”),圆2为异步阻抗圆,圆1和圆2的下边界相同,均为-Xd,圆1的上边界为Xs,圆2的上边界为-0.5X′d。一般建议整定为异步圆,即圆2。按异步圆整定的好处是不必考虑保护误动的问题,即保护装置所配置的各种闭锁均可以取消,如发电机转子电压闭锁、定子电压(或/和母线电压)闭锁、负序电流闭锁、反向无功闭锁、PT 断线闭锁等。当异步阻抗圆与等有功圆不相交时,一般认为应将阻抗圆整定为静稳圆,静稳圆需要配置各种闭锁防止误动。

为了防止误动,一般发电机失磁保护均整定为异步圆,但是当阻抗滑行轨迹没有进入异步圆或者虽然进入了圆内但在圆内滑行时间如果过短,则保护将可能拒动。

发电机失磁后的阻抗轨迹滑入静稳圆没有争议,但在特殊参数接线方式,如超高压或特高压超长输电线路时,送出系统阻抗较大,这种情况的失磁机端测量阻抗能否可靠进入异步圆,存在争议。

等有功阻抗圆示意见图2。

图2 发电机等有功阻抗示意

2 发电机失磁后的阻抗变化分析

发电机瞬态阻抗表达式见式(3)[35],推导过程见《电机瞬态分析》。

式中:Xδ为定转子绕组之间的漏抗;Xad为定转子绕组主磁通回路电抗;XFδ为励磁绕组漏抗;XDδ为阻尼绕组漏抗;ρ=js为海氏计算因子,s为转差率;Xd、Xq为发电机同步直轴、交轴电抗;X′d、X′q为发电机暂态直轴、交轴电抗;X″d、X″q为发电机次暂态直轴、交轴电抗;T′d为发电机直轴暂态时间常数;T″d、T″q为发电机次暂态直轴、交轴时间常数。

对于外部短路故障,当t=0.0 s时,发电机阻抗X=X″d;当t=T″d时,X=X′d。

对于失磁故障,当转子绕组短路失磁,在Ifd衰变过程中,X由负荷感抗衰降约为反向X″d;滑差阶段,X=Xd(ρ)+jXq(ρ),随着转差率的波动,阻抗呈现为不规则圆轨迹。当转差率s稳定时,如调速器可靠调节,轨迹阻抗圆接近于正圆;如不考虑调速器的作用,即当机械转矩Tm不变时,转速将越来越快,s越来越大,这种情况轨迹圆则越滑越小且越接近于葫芦状。因为机械转矩的存在,轨迹圆均偏于第4象限,即轨迹圆的R平均值为正。根据简化的计算可知,s接近或等于0时,X=-Xd;对于汽轮机来说,s最高按-0.1考虑(不考虑转速超过3 300 r/min情况,因为这种情况有超速保护在起作用),对于算例的机组参数,滑差圆的最小阻抗(不考虑负号,下同)X=-0.1Xd≈-X″d。

对于转子绕组开路失磁,开路断口将产生过电压,同时Ifd瞬变为零;对于灭磁开关误分,相当于转子绕组经灭磁电阻短路,Ifd衰变时长与完全短路不同;对于调节器故障,如果功率元件完全关闭,则相当于转子绕组开路,如果是功率元件交流短路,则为关闭和短路交叉状态。

失磁故障形式的不同,影响的仅是异步过程,对机端测量阻抗的滑行圆区域认为影响可忽略,对阻抗影响较大的因素主要是机组参数和失磁前的负载程度,即功角δ和初相角φ。根据分析,负载大小对滑差s数值影响较大,因此如果机组送出系统的阻抗较大,则进入保护异步圆可能略晚。因为失磁后机端阻抗阻抗反向最大值是稳定的,即为-Xd,不同的是反向最小阻抗,因此本文主要对反向最小阻抗影响较大的失磁形式即完全短路失磁进行研究仿真。

3 PSCAD建模仿真计算分析

3.1 仿真模型搭建

与Matlab不同,PSCAD 是专用于电力系统仿真的工具,可以通过图形化的组合,搭建所要计算的机组或电网模型,对各种异常、短路故障等进行仿真计算。本文以660 MW 机组并网到500 k V 电网示例搭建模型,见图3。计算和仿真[5]以某火电厂某台机组为案例,涉及的设备和系统参数为:

图3 发电机组失磁故障仿真计算模型

发电机:汽轮发电机,额定容量660 MW,额定电压20 k V,额定电流21.17 kA,cosφ=0.9,Xd″=0.223 86/0.243 33(饱和/不饱和值),Xd′=0.293 50/0.333 52(饱和/不饱和值),Xd=2.496 24,T″d0=0.046 s,T′d0=8.728 s,T′d=1.026 s,T″d=0.035 s,TJ=3.51;主变压器参数为:Se=810 MVA,额定电压20/525 k V,短路阻抗XT=0.158 7;系统等效参数为:SB=1 000 MVA,UB=525 k V,X1max=0.16,X1min=0.33。

示例中的电厂共有4台机组,通过250 km 的双回500 k V 线路到某500 k V 变电站,经串补电容后再经近200 km 的四回500 k V 线路并入主电网,系统参数已等效到电厂500 k V 母线,因此仿真计算时不再考虑线路阻抗和串补影响等。

机组和电网均按最小方式运行考虑,厂内按1台机组运行考虑。因PSCAD 不能直接测量阻抗,因此由功率和电压测量值进行转换。发电机机端测量阻抗与功率的转换关系,见式(4)。

式中:U、I为机端电压、机端电流,S为视在功率。

式(4)在PSCAD 中的模型应用,见图4。设置失磁保护异步阻抗圆动作元件,模型见图5。图5中的失磁保护异步阻抗圆模块中设置为:圆心为(0,-1.332)p.u.、半径为1.164 p.u.,闭锁电压为0.85 p.u.,保护延时为1.0 s。

图4 功率与阻抗转换模型

图5 失磁保护模型

3.2 发电机重载工况自动控制模式仿真

故障仿真设置的初始时刻为t0=50.0 s,t0之前的时间为软件初始化后的不稳定阶段,需要等各电气输出参数稳定并到达期望数值后才可以开始仿真。按故障前发电机重载考虑,通过调整励调节器磁模块和质量模块(也可使用汽或水轮机+调速器模块)置数,使模型中发电机出力达到要求值。计算时有功送出为P≈576 MW、无功送出Q≈56.7 MVAR,仿真结果显示,失磁后的发电机最大进相无功为约-375 MVAR,失磁后5.4 s阻抗轨迹进入异步圆内,动作后的软件录波见图6。

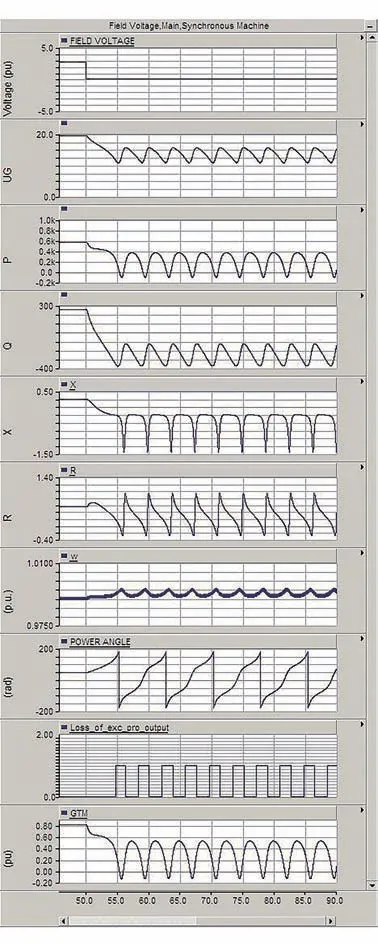
图6 失磁后发电机参数运行变化过程

图6中,FIELD VOLTAGE 为转子电压(单位:p.u.,对应空载额定转子电压),P、Q为机端有功、无功功率(正为送出,单位:MW、Mvar);X、R为机端测量阻抗(单位:p.u.,对应额定阻抗),UG为机端线电压(单位:k V),Loadangle为功角(单位:°);w为转速、GTM为机械转矩控制参数,单位均为p.u.,对应额定转速;Loss_of_exc_pro_output为模拟的失磁保护输出(值1表示保护动作)。

将X、R置于同一坐标平面的阻抗滑行轨迹见图7。根据计算所使用的参数,画在同一坐标平面的100%等有功圆与异步阻抗圆见图7。

图7 机械转矩自动模式重载工况滑行轨迹

圆心坐标为:Dy=Xs=XT +Xsmin=0.386

圆半径为:r=Dx

异步阻抗圆坐标为:Dx=0

由图7可看出,等有功圆与异步圆虽不交叉,但异步后阻抗轨迹仍可以可靠进入异步圆,但存在周期性进出异步圆的现象,因此保护的整定延时不宜太长。

3.3 发电机重载工况恒机械转矩模式仿真

故障前机组出力负荷保持不变,将机械转矩改恒值控制,即汽轮机(或水轮机)原动力不变,则完全失磁的滑行轨迹见图8。

图8 机械转矩恒值控制模式滑行轨迹

从图8可看出,因为机械转矩为恒值,失磁后机组进入异步状态后,转速越来越快,阻抗圆是逐渐收缩的形态,轨迹在异步圆的穿越时间更短。

3.4 发电机轻载自动控制模式仿真

机械转矩控制方式为自动调节方式,将故障前机组出力负荷改为轻载,计算时有功送出为P≈211 MW、无功送出Q≈36 Mvar,则完全失磁滑行轨迹见图9。

图9 机械转矩自动模式轻载工况滑行轨迹

从图9可看出,机组轻载工况自动控制模式失磁后,阻抗轨迹滑入异步圆的时间稍晚,停留时间也稍长。

4 结论

并列到交流电网的发电机组,如果正常运行机组出力不受限,则失磁保护不论等有功圆与异步圆是否相交,根据仿真结果,异步圆的失磁保护均能动作出口。当失磁保护阻抗圆整定选取为静稳圆时,应注意设置必要的闭锁条件,包括机端电压(或系统电压)、PT 断线、转子电压、负序电流、无功方向等,防止保护误动。当取为异步圆时,这些闭锁条件可以取消。

当机组与系统联系阻抗超级大时,机组失磁后阻抗滑行轨迹不呈现为圆特性,滑行贴近纵轴时不再异步滑行,但仍可进入异步阻抗圆。保护延时延时不宜取值过大,按本文参数仿真计算的保护动作脉冲为2.6 s,综合考虑认为,保护延时不应大于1.0 s。闭锁机端电压取0.85 p.u.已可可靠闭锁/开放失磁保护,调升到0.9 p.u.必要性不大。阻抗圆的下边界取Xd,已满足各种情况的失磁故障,调升到Xd+0.5X′d的必要性不大。