前飞来流和侧风对植保无人机下洗流场影响的数值模拟研究*

胡聪旭，周建平, 2, 3，刘新德，许燕, 2

(1．新疆大学机械工程学院，乌鲁木齐市，830047； 2． 新疆维吾尔自治区农牧机器人及智能 装备工程研究中心，乌鲁木齐市，830047； 3． 新疆大学叶城核桃产业研究院，新疆叶城，844900)

0 引言

在农业植保方面，植保无人机受到越来越多的关注，因此的植保无人机相关技术发展尤为迅速，由于植保无人机具有高效、灵活、喷施效果好、地形适应性强等优势[1-4]，植保无人机应用现已引起更多更广泛的关注。目前，在航空植保领域我国95%的航空技术已经应用于田间病虫害防治，其他的主要用于农情信息获取，相关航空影像拍摄和不同种类农作物育种等[5-6]。植保无人机作业方面更多的关注雾滴和喷洒系统[7]，但缺乏对下洗流场具体结构特性深入了解。植保无人机喷洒作业时下洗流场对雾滴作用至关重要，由于环境侧风和前飞来风对下洗流场的影响，导致下洗流场流动紊乱和结构复杂，还会产生后方和侧方滞后现象，造成到药液飘移和喷洒不均。此外，还会影响植保无人机自动化作业路径规划，造成自动化作业需要人工辅助和喷洒不均等。由此，有必要开展前飞来流和侧风对植保无人机下洗流场影响研究。

在探究植保无人机雾滴沉积、飘移和喷幅方面，张京等[8]、杨知伦等[9]、王昌陵等[10]和Shi等[11]以及国内外研究者已进行较为广泛的研究。文晟等[12]解释了旋翼尖端涡流形成原因。目前对植保无人机下洗流场的研究手段主要有直接测量、间接测量和计算流体力学(Computational fluiddynamic，CFD)[13-15]。为进一步观察到下洗流场详细流动情况，Tang等[16]和Ramasamy等[17]利用数字粒子图像测速法精准捕捉旋翼下洗流场，分析了涡流现象、流场速度衰减率和悬停高度与轴径向速度之间的关系，观察到可能导致液滴飘移的突发型流动结构。

现有的直接测量和间接测量方法都是从实验角度出发的，存在实验周期长和资源消耗大等弊端，且由于下洗流场结构发展具有复杂性，传统技术手段无法获取整体流场信息。随着计算流体力学的不断发展，通过仿真计算能够得到整个植保无人机下洗流场流动信息，为进一步研究植保无人机下洗流场提供了更加便捷的技术手段。Tang等[18]为进一步研究植保无人机下洗流场及其影响下的液滴运动规律，采用格子Boltzmann方法对植保无人机下洗流场和雾滴运动进行了模拟仿真，得到了植保无人机下洗流场整体结构和最终液滴分布是非对称的，更进一步得出，雾滴沉积的变化系数会随着应用高度的增加而减小，使雾滴沉积更加均匀，但损失了雾滴沉积质量。 Zhang等[19]采用基于细观动力学的格子Boltzmann方法(LBM)对植保无人机下洗流场进行模拟仿真，对悬停和前飞情况下洗流场的气流分离特性、气流覆盖等效面积和“陡坡”效应进行了数值研究，结果表明飞行速度和飞行高度对植保无人机下洗流场的分布有显著影响。

研究证实计算流体力学方法满足植保无人机下洗流场研究需求，数值模拟结果具有较高精度，且比传统实验方法更容易捕捉到植保无人机下洗流场细节。研究发现植保无人机下洗流场具有复杂性，并在植保无人机作业中直接影响到雾滴。采用格子Boltzmann方法数值模拟单旋翼植保无人机有无侧风影响的前飞下洗流场，深入研究单旋翼植保无人机下洗流场流动结构受前飞来流和侧风影响程度，为进一步研究旋翼植保无人机作业时雾滴运动规律、沉积均匀性和飘移特性奠定基础。此外，还能为植保无人机喷洒作业路径规划提供指导。

1 物理模型

研究对象为CopterWorks AF25B 型油动力植保无人直升机[20]，其载重量可达15 kg，详细参数如表1。使用SolidWorks创建其全尺寸简化模型如图1，所建立的模型包括全尺寸螺旋桨和不包含尾桨和着陆支架的全尺寸机身，其中：螺旋桨翼为 NACA 2415型，总长度为2.15 m，弦长0.071 m桨身无扭转，攻角为6°；不包含尾翼和着陆支架的全尺寸机身外形尺寸为0.60 m×0.40 m×0.37 m。在本次模拟仿真中坐标系定义为：X轴正方向为植保无人直升机右面，Y轴正方向为上升方向，Z轴负方向为植保无人直升机的前进方向。

(a) CopterWorks AF25B 型油动力植保无人直升机

(b) 简化模型图1 AF-25B型植保无人机Fig. 1 Picture of AF-25B plant protection UAV

表1 Copterworks AF25B型油动力植保无人直升机主要性能参数Tab. 1 Main performance parameters of Copterworks AF25B oil-powered plant protection UAV

2 数值模拟理论与方法

传统的计算流体力学(CFD)方法已被广泛应用于物体旋转运动产生的流场特性研究中，如今已有ANSYS Fulent、CFX、COMSOL和OpenFOAM等商业和开源软件均已成功应用于流场仿真中。传统计算流体力学方法在进行仿真实验之前都必不可少进行仿真区域和模型网格划分前处理，网格质量的好坏决定计算结果的精确性。在仿真旋转运动产生的流场过程中常使用动网格技术，传统计算流体力学技术已有广泛研究，但在应用于无人机旋翼产生的下洗流场这种复杂边界条件研究中还存在着网格重构的困难，导致仿真实验中计算错误和无法更进一步获取旋翼下洗流场特征。

本文采用基于格子Boltzmann方法的XFlow (Next Limit Dynamics S. L.) 软件对前飞来流和侧风对植保影响的无人机下洗流场数值模拟研究。格子Boltzmann方法的流体仿真技术由McNamara和Zsnetti于1988年提出[21]，近年来越发受到关注。格子Boltzmann方法在研究针对具有复杂边界条件且为外流场的植保无人机下洗流场方面比传统CFD方法更具有优势[22]。此外，在利用格子Boltzmann方法进行植保无人机下洗流场仿真过程中，不需考虑传统CFD方法的网格划分步骤，这得益于格子Boltzmann方法是基于粒子的计算方法。

2.1 格子Boltzmann方法

格子Boltzmann方法是在介观模拟尺度上对相应模拟问题进行四阶离散化，对模拟问题进行计算的方法，且相比于传统CFD方法其更容易实现对复杂结构的仿真计算。由于本研究针对植保无人机下洗流场侧风前飞情况属于三维模拟仿真，在XFlow中对三维外流场仿真主要使用D3Q27(图2)特征晶格结构进行求解。该特征晶格结构特征是将速度空间离散化为有限个数的离散速度(ei=0, 1, 2,…, 25)。格子Boltzmann方法使用格子Boltzmann方程作为最终求解方程，将其在晶格上离散化的方程[23]

fi(x+ei,t+dt)=fi(x,t)+Wi(x,t)

(1)

(2)

式中：fi——第i个方向上粒子的速度分布函数；

ei——沿着第i个方向的速度；

dt——时间步长；

fi(x，t)——t时刻x点处第i个方向上的粒子速度分布函数；

Hi——碰撞算子；

fie——单粒子平衡态分布函数；

τ——无量纲松弛参数。

图2 D3Q27离散速度模型Fig. 2 D3Q27 discrete velocity model

2.2 湍流模型

本文使用自适应壁面局部涡(WALE)黏度模型对单旋翼植保无人机下洗流场模拟仿真，该模型恢复了湍流边界层可以直接求解的渐近特性，来获得单旋翼植保无人机下洗流场特性。且采用自适应壁面局部涡黏度模型以节省计算资源。相应WALE数学模型

(3)

式中:Vturbulent——模拟亚格湍流的湍流涡流黏度；

Δ ——滤波器尺度；

Cw——常数，通常取 0.325；

Vol——单位网格尺度；

Sjk、Gjkd——分辨尺度应变率张量；

δjk——克罗内克尔符号；

gjk、gkj、gγγ——应变率张量，可用格子Boltzmann方法作二阶矩获得。

j、k、γ——根据空间维度可取值1，2，3。

2.3 速度矢量合成理论

在对前飞来流和侧风对植保影响的无人机下洗流场数值模拟中，机身和旋翼往往无法得到理想的同步移动，使其在计算区域移动也将花费巨大计算量，极大降低了计算效率。分析可知，植保无人机在前飞中存在相对风速，这是造成植保无人机喷洒过程中下洗流场和喷雾雾滴滞后现象的重要原因[24]，而侧向风则是导致流场偏离航线的主要因素。因此，使植保无人机停留在固定位置，施加环境风的方式实现下洗流场滞后现象和环境侧向风对植保无人机下洗流场影响的模拟仿真。相应的三维风速矢量合成理论描述和矢量合成示意图如图3,其原理如式(4)所示。

(4)

式中：V——风速；

Vx——x轴上的速度分量；

Vy——y轴上的速度分量；

Vz——z轴上的速度分量。

图3 风矢量合成示意图Fig. 3 Wind vector synthesis diagram

2.4 边界条件

设置如图4长方体数字风洞x，y，z方向上对应的尺寸为20 m×5 m×20 m作为计算域。在整个仿真实验中，将单旋翼植保无人机正下方边界设置为壁面，速度入口设置为进风口，速度出口设置为出风口，相关风向根据实际情况设置；根据单旋翼植保无人机实际作业飞行速度和适合作业的环境风速，将飞行速度分别设置为1 m/s、3 m/s、5 m/s、7 m/s，侧向风速分别取软风、微风、清风和和风对应的1 m/s、3 m/s、5 m/s、7 m/s。

为使得数值模拟研究更具有代表性，选用单旋翼植保无人机飞行高度为旋翼半径的2～3倍，计算中设置旋翼距离地面1.5 m、2.5 m和3 m[25-26]。为保证植保无人机下洗流场在计算域中完全发展，其放置于计算域中的位置应合理选择，如图4所示单旋翼植保无人机放置位置示例，具体为x=-5 m，y=2.5 m，z=-5 m处。

(a) 俯视图

(b) 轴测图图4 20 m×5 m×20 m长方体数字风洞计算域Fig. 4 20 m×5 m×20 m cuboid digital wind tunnel computational domain

使用计算与局部细化的方式来获得单旋翼植保无人机下洗流场的不规则的湍流流动。为对整体模型采用壁面自适应局部涡黏度模型(WALE)，来提高仿真的准确性；为节省计算资源和计算时间，将整体计算分辨率设置为0.5 m；为进一步得到植保无人机下洗流场的流动特性和尾迹涡流，针对机身、旋翼细化算法和涡流尾迹采用自适应细化算法，且机身细化分辨率、旋翼细化分辨率为和涡流尾迹细化分辨率均设置为0.031，其中涡流尾迹细化阈值设定为5×10-5m。最终将风洞计算域划分为5个等级，细化结果如图5所示，且在计算过程中细化区域会随植保无人机下洗流场的延伸而扩展。

图5 风洞计算域细化结果Fig. 5 Wind tunnel calculation domain refinement results

3 结果与分析

3.1 数值模拟可行性分析

在针对单旋翼植保无人机下洗流场研究过程中存在许多限制。其中，对单旋翼植保无人机在野外进行飞行作业时下洗流场的实验存在诸多限制，现有技术手段很难实现以实验捕捉瞬时速度场和更多细节。唐庆等[25]利用粒子图像测速法实现了对比例为1∶10的单旋翼植保无人机悬停情况下洗流场时间分辨率(小于0.005 m)和空间分辨率(小于0.001 s)室内捕捉[27]，在进一步研究中，将单旋翼植保无人机悬停情况的下洗流场格子Boltzmann方法数值模拟结果与室内粒子图像测速法获得的结果对比，结果显示，该数值模拟模型能精确模拟单旋翼植保无人机下洗流场，且相比与传统CFD方法还能捕捉到更多流场细节[18, 20]，为后续深入研究单旋翼植保无人机下洗流场研究奠定了基础。

3.2 无侧风前飞下洗流场分析

3.2.1 无侧风前飞下洗流场整体分析

为探究单旋翼植保无人机在无侧风情况下来流对旋翼下洗流场的影响，针对飞行高度2.5 m和飞行速度分别为1 m/s、3 m/s、5 m/s、7 m/s进行数值模拟并分析。图6为单旋翼植保无人机前飞1.6 s时的下洗流场涡量云图。由6可知，前飞速度较低(速度为1 m/s和3 m/s)时，旋翼产生的下洗流场受前飞来流的影响较低，在与地面撞击后发展成与悬停时流动情况类似的流场形态；处于单旋翼植保无人机前侧的地面涡与前飞来流耦合，使得地面涡比其他位置更容易出现非规则畸变，并率先形成最终紊流状态[12]。当前飞速度增加到较高速度时(前飞速度为5 m/s、7 m/s)，前飞来流将会导致下洗流场明显的滞后现象，下洗流场俯视图呈现与速度较低时完全不同的小扇形，且显示出下洗流场尾迹不对称性，伴随着出现螺旋涡尾迹。

这种结构的不对称性可能时由于翼尖与前飞来流的相对速度不同引起的[18]。当单旋翼植保无人机悬停时，其翼尖速度计算为。在单旋翼植保无人机飞过程中，旋翼两端将各自出现向后和向前的速度，由此旋翼两端翼尖速度可以计算为悬停时的翼尖速度加上或减去前飞速度。当前飞速度到达一定值时将导致明显的速度差，导致两侧抗风性不同，最终表现为旋翼尾迹不对称性。前飞时产生的螺旋涡尾将导致雾滴喷出后卷扬如图7。

(a) 1 m/s

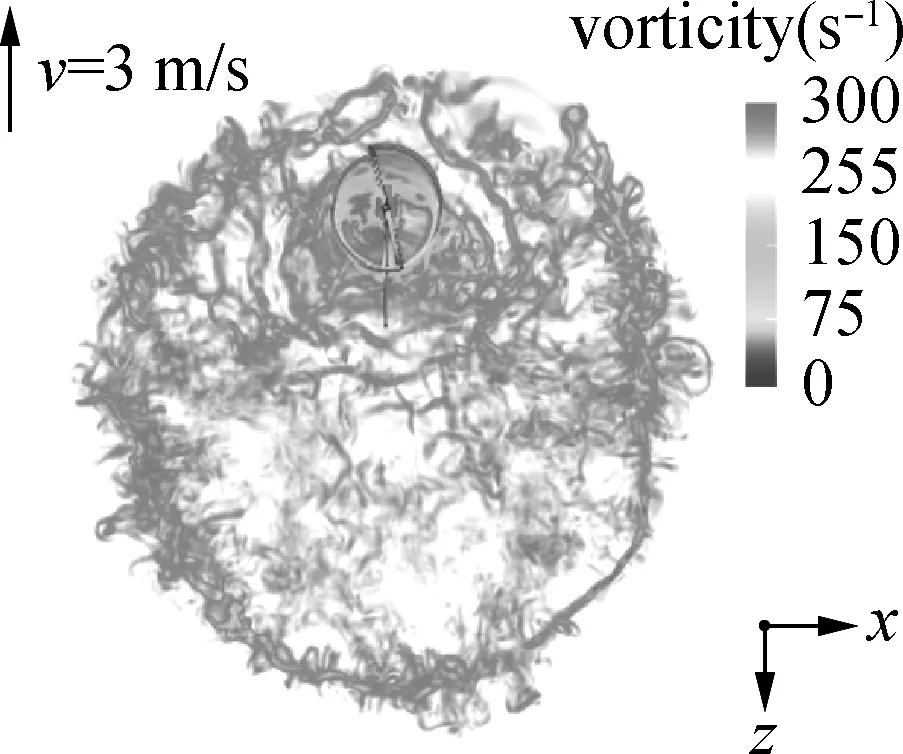
(b) 3 m/s

(c) 5 m/s

(d) 7 m/s图6 高度为2.5 m的无侧风前飞下洗流场涡量图Fig. 6 Vorticity diagram of forward flying airflow field without crosswind at a height of 2.5 m

图7 下洗流场螺旋涡尾迹导致的喷雾卷扬Fig. 7 Spray winch caused by spiral vortex wake in airflow field

3.2.2 无侧风时不同前飞速度对下洗流场形态影响

图8是单旋翼植保无人机无侧风时且飞行高度2.5 m和飞行速度分别为1 m/s、3 m/s、5 m/s和7 m/s时的下洗流场涡量矢量图，进一步表示了无侧风情况的单旋翼植保无人机下洗流场特征。当单旋翼植保无人机前飞速度由1 m/s增加到7 m/s过程中，前飞速度为1 m/s时不会引起下洗流场倾斜；当前飞速度增大到3 m/s后，前飞速度造成下洗流场倾斜程度逐渐凸显，在设定的前飞速度范围内使下洗流场向后倾斜0°～52°；在前飞速度从3 m/s增加到7 m/s过程中，下洗流场倾斜角度增大了116.67%。特别的，当前飞速度达到7 m/s时下洗流场发生二次偏移，使下洗流场倾斜角度达到71°。

进一步分析可知，随着前飞速度的增大，单旋翼植保无人机下洗流场前端地面涡效应逐渐降低，从前飞速度1 m/s和3 m/s时的向前延伸到5 m/s和7 m/s的消失，对前飞来流失去抵抗能力。由此可得，造成上述剧烈二次偏移的原因是用于当单旋翼植保无人机前飞速度增大到7 m/s时，速度向外的地面涡效应消失，导致最终下洗流场倾斜角度扩大。可以预测到，这将造成最终在施药作业中雾滴的严重滞后，更进一步由于环境风的作用造成雾滴飘移至非靶标作物甚至更远[12]，最终引起施药效果差，且造成环境污染。

(a) 1 m/s

(b) 3 m/s

(c) 5 m/s

(d) 7 m/s图8 飞行高度2.5 m时不同前飞速度滞后距离及 角度变化Fig. 8 Delay distance and angle variation of different forward velocities at flight altitude of 2.5 m

在单旋翼植保无人机前飞作业中，从图9 (a)和图9 (b)中可以观察到前飞来流与旋翼产生的下洗流场之间相互作用使得单旋翼植保无人机前端下洗流场外侧流速急剧减小。更进一步的由图10分析可得，这种现象是由于旋翼旋转产生涡尾迹，这种涡尾迹更多的存在于旋翼的前侧和后侧下方，且旋向都向外。单旋翼植保无人机前飞时，前飞来流方向将与形成的前侧涡尾迹旋向相反，产生流速抵消现象。最终可得，在存在侧风时这种抵消现象将使得单旋翼植保无人机拥有更好的抗风性。

(a) 3 m/s

(b) 5 m/s图9 单旋翼植保无人机不同前飞速度下洗流场速度云图Fig. 9 Cloud image of airflow field velocity of a single rotor plant protection UAV with different forward flights peed

图10 前飞时前方流速急剧减小理论图Fig. 10 Theoretical diagram of sharp reduction of forward velocity during forward flight

3.2.3 无侧风时不同前飞速度对下洗流场流速影响

在单旋翼植保无人机无侧风前飞过程中，前飞来流是影响稳定情况的下洗流场形态的关键因素，也是造成下洗流场速度变化的重要原因。由图11所示，当以不同前飞速度作业时，旋翼所产生的下洗流场流速将受影响呈现“M”形[28]。前飞高度一定时，随着前飞速度的增加，下洗流场的两侧峰值流速间距将缩小，峰值速度出现位置与旋翼轴心距离将增大。随着下洗流场流速的后移，单旋翼植保无人机在进行植保作业时喷雾雾滴也会随之后移，且位于峰值速度区域雾滴流速也最快。因此，改变单旋翼植保无人机的前飞速度不能改变单旋翼植保无人机喷施作业时雾滴的均匀性。

此外，当前飞速度增大到7 m/s时，单旋翼植保无人机下洗流场上述双流速峰值将会消失，下洗流场流动情况变得复杂，“M”形流速消失。这不能作为使喷洒中雾滴更均匀的方式，因为前文提到的前飞速度过大会造成流场滞后严重，会造成更多的液滴飘移至靶标作物外。

图11 飞行高度2.5 m时不同前飞速度导致的下洗 流场速度变化Fig. 11 Velocity variation of airflow field caused by different forward velocities at flight altitude of 2.5 m

3.3 受侧风影响的前飞下洗流场分析

单旋翼植保无人机在实际作业中受到环境风影响不可避免，现有对无外界环境风干扰情况的下洗流场研究与实际作业还存在巨大差距。从无侧风前飞下洗流场分析中可知，受前飞来流影响的下洗流场将产生滞后现象，且随着前飞速度的增大，下洗流场滞后距离将增大。在喷洒作业时，这种现象将影响单旋翼植保无人机喷雾覆盖区域。由此，在无环境风干扰情况的下洗流场研究基础上对有侧风前飞下洗流场流动特性和风速分布情况展开研究，更全面揭示单旋翼植保无人机下洗流场在侧风影响下的运动规律，为进一步研究单旋翼植保无人机喷洒作业时下洗流场对雾滴运动规律的影响奠定基础。

3.3.1 受侧风影响的前飞下洗流场整体分析

为探究受侧风影响的前飞下洗流场流动结构，选取并分析飞行高度为2.5 m、前飞速度为5 m/s和受不同侧风风速影响的下洗流场。图12为受不同侧风影响的前飞下洗流场流动结构角β和偏角α表示图，其中图12(a)表示无侧风时前飞下洗流场，图12(b)、图12(c)、图12(d)和图12(e)分别对应侧风速为1 m/s、3 m/s、5 m/s和7 m/s。分析可得，在无侧风前飞时下洗流场也会出现偏角，是由于旋翼左右两侧得速度差造成的(如3.2.1节所述)；随着侧风速度不断增大，下洗流场向右偏角不断增大，从无侧风情况的偏角3°一直增大到侧风速度7 m/s时的56°，由此可知，前飞下洗流场偏转角度与侧风速度大小成正比。此外，侧风速度还影响下洗流场的流动结构角，在侧风速度由0 m/s增大到7 m/s过程中，流动结构角从80°减小到42°，由此可知，前飞下洗流场偏转角度与侧风速度大小成反比。图12(a)和图12(b)中显示的流动结构左右边缘向内弯曲，是由于前飞速度为5 m/s时，下洗流场向后偏移较少，下洗流场撞击地面所形成，而当侧风速度较快时，该弯曲结构消失(如图12(c)和图12(d)所示)。

(a) 侧风速度0 m/s

(b) 侧风速度1 m/s

(c) 侧风速度3 m/s

(d) 侧风速度5 m/s

(e) 侧风速度7 m/s图12 受不同侧风速(风向从左向右)影响的前飞下洗 流场流动结构和偏角表示图Fig. 12 Figure of flow structure β and deflection Angle α in the forward airflow field affected by different lateral wind speeds (wind direction from left to right)

3.3.2 有无侧风影响的前飞下洗流场对比分析

图13为单旋翼植保无人机无侧风前飞和侧风影响下前飞下洗流场速度分布云图。其中，图13(a)和图13(b)中飞行高度均为2.5 m；图13(a)表示前飞速度5 m/s侧风速度3 m/s情况的下洗流场速度分布云图；图13(b)为前飞速度5 m/s无侧风情况的下洗流场速度分布云图，且图13(a)和图13(b)中每幅图间隔为1 m选取。对比分析可知，当单旋翼植保无人机以5 m/s速度前飞中，侧风对下洗流场的形态影响较小，整体上下洗流场形态在侧风影响情况下仍然保持良好，有无侧风均呈现“U”形结构。该“U”形结构主要呈现出在“U”形半包围轨迹上速度较高，中间速度较低。此外，从图像色彩值可以清晰观察到有侧风影响时，随着与旋翼距离增大尾迹速度越接近前飞和侧风速度矢量和，这表明存在侧风时喷雾雾滴更容易产生飘移。

and downwash flow field of single rotary wing plant

protection UAV under the influence of different crosswinds

3.3.3 侧风速度与下洗流场偏移量间关系

图14显示了单旋翼植保无人机下洗流场在x与z轴方向上的下洗流场偏移量测量原理。该方法主要通过测量与形成下洗流场边界平行线与地面相交点到过旋翼尖端作垂直于地面的直线与地面间的交点间的距离，最终分别获取到下洗流场的x与z轴方向上的下洗流场偏移量。

图14 x与z轴方向上的下洗流场偏移距离测量原理Fig. 14 Measuring principle of airflow field offset distance in x and z axis direction

图15 侧风前飞下洗流场x轴偏移量Fig. 15 x-axis offset of flying airflow field before crosswind

图16 侧风前飞下洗流场z轴偏移量Fig. 16 z-axis offset of flying airflow field before crosswind

图15为侧风前飞下洗流场x轴偏移量直方图，从图中我们可以非常直接观察到当单旋翼植保无人机前飞速度一定时，侧风的增大，将直接导致侧风前飞下洗流场x轴偏移量增大，且侧风风速越大造成下洗流场x轴偏移程度也越明显。值得注意的是，当侧风速度相对较低时，相同侧风速度引起不同前飞速度产生的下洗流场x轴偏移并不明显。当前飞速度为1 m/s时，不同侧风速度下的下洗流场x轴偏移量服从二阶规律Xa=0.03v2+0.35v-0.13；当前飞速度分别为3 m/s、5 m/s和7 m/s时，对应的规律分别为Xb=0.05v2+0.23v+0.19、Xc=0.04v2+0.30v+0.05和Xd=-0.01v2+0.85v-0.07。

图16为侧风前飞下洗流场z轴偏移量直方图，观察可得下洗流场在相同前飞速度下z轴偏移量受侧风速度改变影响波动较小；经分析，由于前飞下洗流场在侧风作用下存在一定得偏转(如3.3.1节所述)，偏角的增大和下洗流场与地面接触点增加，最终导致得到z轴偏移量受侧风速度改变影响波动较小的数据结果。两图中均出现了当速度较小时，并未出现下洗流场偏移的现象，可能是由于单旋翼植保无人机下洗流场具有抗风性。

在使用单旋翼植保无人机作业时应当综合考虑多方面因素，尤其是单旋翼植保无人机作业时的前飞速度以及当时的环境风速。综上所述，单旋翼植保无人机作业的最佳前飞速度区间和最佳环境侧风速度区间分别为1～5 m/s和0～5 m/s。在选择合适的前飞速度情况下，此种单旋翼植保无人机能在无风、软风、微风和清风环境下完成植保作业工作。

4 结论

本文主要利用格子Boltzmann方法模拟单旋翼植保无人机不同前飞速度影响下的瞬时下洗流场和存在不同侧风速度时不同前飞速度影响下的瞬时下洗流场。主要研究分析结果总结如下。

1) 单旋翼植保无人机在前飞过程中将产生螺旋形尾迹，由于旋翼尖端速度差引起尾迹在前飞中呈现不对称分布，对雾滴运动、漂移和均匀性等存在影响。单旋翼植保无人机下洗流场具有抗风性是由于前飞来流方向与形成的前侧涡尾迹旋向相反，产生流速抵消现象。在单旋翼植保无人机前飞高度一定时，前飞速度从3 m/s增大到7 m/s，洗流场倾斜角度增大116.67%，倾斜角度达到71°，且还会发生二次偏移。

2) 单旋翼植保无人机下洗流场流速呈“M”形。前飞高度一定时，随着前飞速度的增加，下洗流场的两侧峰值流速间距将缩小，峰值速度出现位置与旋翼轴心距离将增大；当前飞速度增大到7 m/s时，单旋翼植保无人机下洗流场上述双流速峰值将会消失，下洗流场流动情况变得复杂，“M”形流速消失。

3) 在侧风影响的相同前飞高度和前飞速度情况下，单旋翼植保无人机下洗流场随着侧风的增大出现不同角度的偏转，且角度与侧风速度成正比；下洗流场流动结构与无侧风时相同，都呈“U”形结构；在相同前飞高度和速度下，当前飞速度为1 m/s、3 m/s、5 m/s和7 m/s时，下洗流场x轴偏移量可用Xa=0.03v2+0.35v-0.13、Xb=0.05v2+0.23v+0.19、Xc=0.04v2+0.30v+0.05和Xd=-0.01v2+0.85v-0.07拟合，可见不同侧风速度下的下洗流场x轴偏移量服从二阶规律。