高压下菱镁矿的弹性性质

祁建宏，郭 媛

(兰州城市学院信息工程学院，甘肃兰州 730070)

菱镁矿是地幔中碳酸盐的主要宿主，在地幔中碳的输运和储存中起着重要作用，其高压物理特性对于理解深层碳循环至关重要．最近的研究结果表明，菱镁矿在压强低于85 GPa的地幔范围内是稳定的[1-4]．

矿物的弹性常数控制着弹性载荷下的应力-应变关系，并与理解强度、硬度、脆性/延展性、损伤容限和力学稳定性相关．弹性模量控制着弹性波的传播，包括地壳和地幔的地震各向异性，因此对地震数据的解释非常重要．作为自由能的衍生物，它们也与矿物的热力学性质相关，对理解状态方程、相稳定性和相变机制很重要[5]．然而，在高温高压下测量弹性常数非常困难．目前，仅测得在300 K，压强上升到13.7 GPa时，菱镁矿的弹性常数[6]．理论上，Yao等[7]利用局域密度近似(LDA)的第一性原理计算了地幔条件下菱镁矿的热力学和弹性特性；Li等[8]基于密度泛函理论研究了Mg1-xFexCO3的高压、高温相的稳定性；Stekiel等[9]使用广义梯度近似(GGA)的第一性原理计算了FeCO3-MgCO3碳酸盐的高压弹性;Marcondes等[10]利用局域密度近似(LDA)和广义梯度近似(GGA)的第一性原理密度泛函理论研究了MgCO3,CaCO3和MgCa(CO3)2的高压结构和弹性性质．这些研究主要讨论了菱镁矿的弹性性质和弹性波速．

文中将广义梯度近似(GGA)的交换相关势采用更适合固体性质研究的Perdew-Burke-Ernzerhof for solid(PBEsol)代替，利用基于密度泛函理论第一性原理计算的投影缀加平面波(PAW)方法研究了高压下菱镁矿的弹性性质，得到了菱镁矿弹性各向异性的性质．

1 计算方法

文中采用基于密度泛函理论的VASP软件包[11-12]进行第一性原理计算，PAW描述离子实和价带子间的相互作用[13]，广义梯度近似的PBEsol泛函描述电子交换关联作用[14]．通过收敛测试，平面波的截断能为560 eV，能量收敛标准为10-6eV，力收敛标准为0.001 eV·nm-1.布里渊区取样采用8×8×8的Monkhorst-Pack方法[15]进行k点网格几何优化．

1.1 弹性常数

在无穷小应变下,应力应变关系满足Hooke定律[16-17]

σij=cijεkl,

(1)

其中,σij和εkl为应力和应变张量的分量；cijkl为4阶弹性刚度张量系数.由于应力和应变张量的对称性，Hooke定律可表示为矩阵方程

σi=cijεj,

(2)

其中,cij为弹性常数的张量.对属于菱面体系统的菱镁矿弹性矩阵可表示为

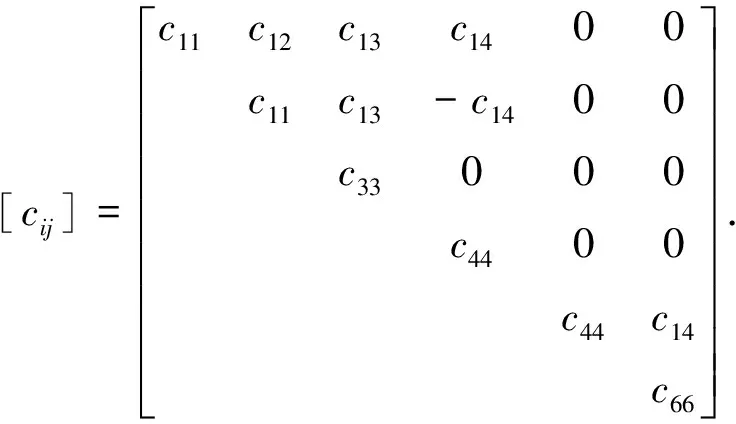
(3)

1.2 Birch-Murnaghan状态方程

Birch-Murnaghan状态方程模型是地球物理学中使用最多的状态方程模型.3阶Birch-Murnaghan状态方程为[18]

2 结果与讨论

2.1 晶格参数和状态方程

表1给出了计算的菱镁矿晶格参数、体积模量以及压强的导数，并和前面报道的实验数据[19-22]进行了比较，其他实验和理论结果见文献[7]和[23].可以看出，目前的计算结果与先前报道的结果非常吻合．

表1 菱镁矿的晶格参数

矿物的状态方程有助于模拟地球深层的组成．计算的菱镁矿状态方程如图1所示．压强从0到90 GPa时状态方程与之前的实验数据[21,24-25]一致．晶格参数和状态方程与实验的一致性为计算方法的可行性和可靠性提供了保证．

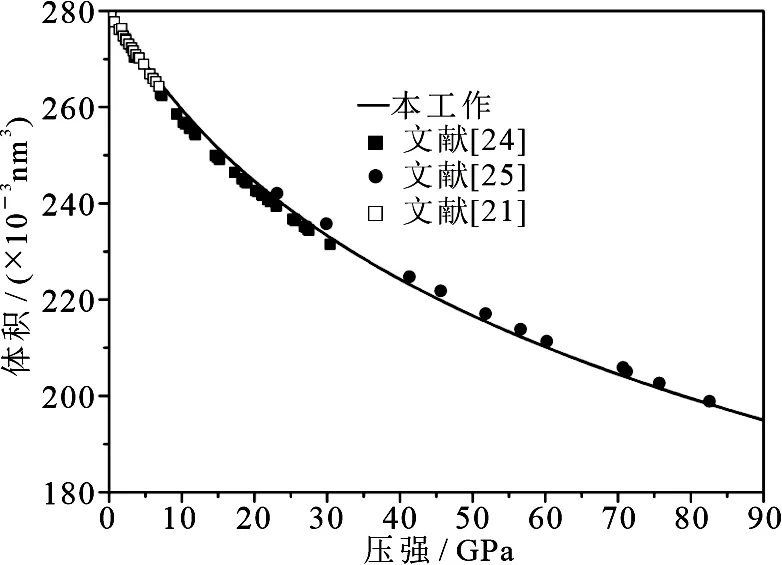
图1 菱镁矿的体积随压强的变化

2.2 弹性常数和弹性模量

文中计算的所有弹性刚度常数都满足力学稳定性标准．

菱镁矿高压弹性常数如图2所示，与Yang等[6]的实验结果非常符合，并且随着压力的增加而增大．从图3沿不同轴的线性压缩可观察到，由于在整个研究的压强范围内c11大于c33，表明沿着c轴的压缩大于沿着a轴的．由于c11=c22≠c33，菱镁矿的弹性常数是各向异性的，这将导致弹性模量的各向异性．

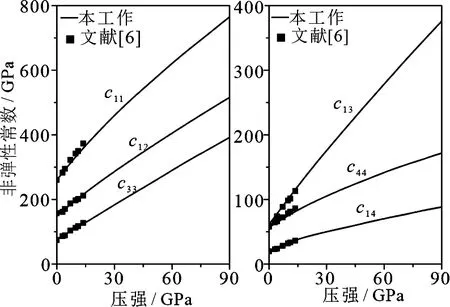
图2 菱镁矿的弹性常数

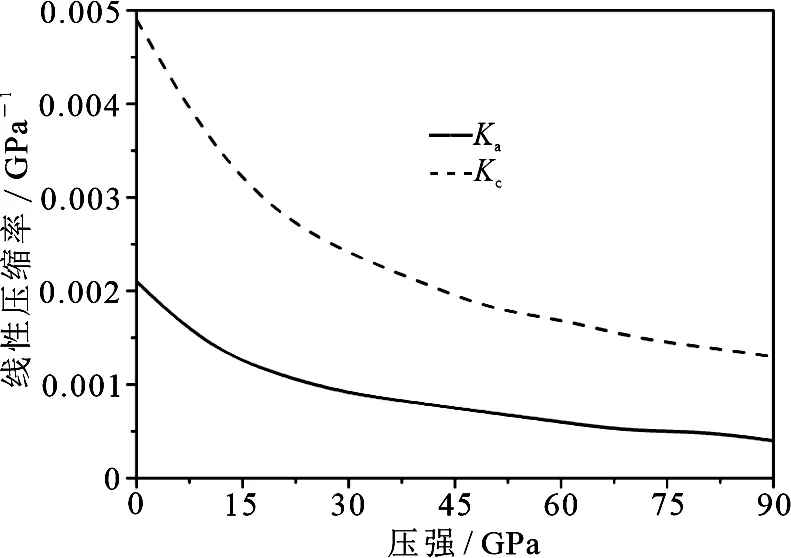
图3 菱镁矿的线性压缩

菱镁矿的体积模量(B)、剪切模量(G)和杨氏模量(E)使用Hill平均方法计算[27]:

(7)

下标V和R分别为Voigt近似[28]和Reuss近似[29]．使用下面的公式计算[30]:

菱镁矿的体积模量B、剪切模量G和杨氏模量E与之前的实验结果[6]比较如图4所示．弹性模量随着压力的增加平滑单调地增加，与实验符合地很好．

图4 菱镁矿的体积模量B、剪切模量G和杨氏模量E

2.3 弹性各向异性

为了评估菱镁矿的弹性各向异性，文中采用通用各向异性指数AU作为各向异性的量度，AU可表示为[31]

AU=0表示弹性各向同性，值越大表示弹性各向异性越高．菱镁矿的通用各向异性指数如图5所示,可以看出，AU随着压力的增加而增大，意味着菱镁矿在高压下具有大的弹性各向异性．

图5 菱镁矿的通用各向异性指数

为了显示压力对菱镁矿各向异性的影响，利用ELATE程序[32]得到了三维空间的剪切模量和杨氏模量，不同压强下的结果如图6和图7所示．这些模量表现出与方向相关的较强变化，导致菱镁矿出现大的各向异性．

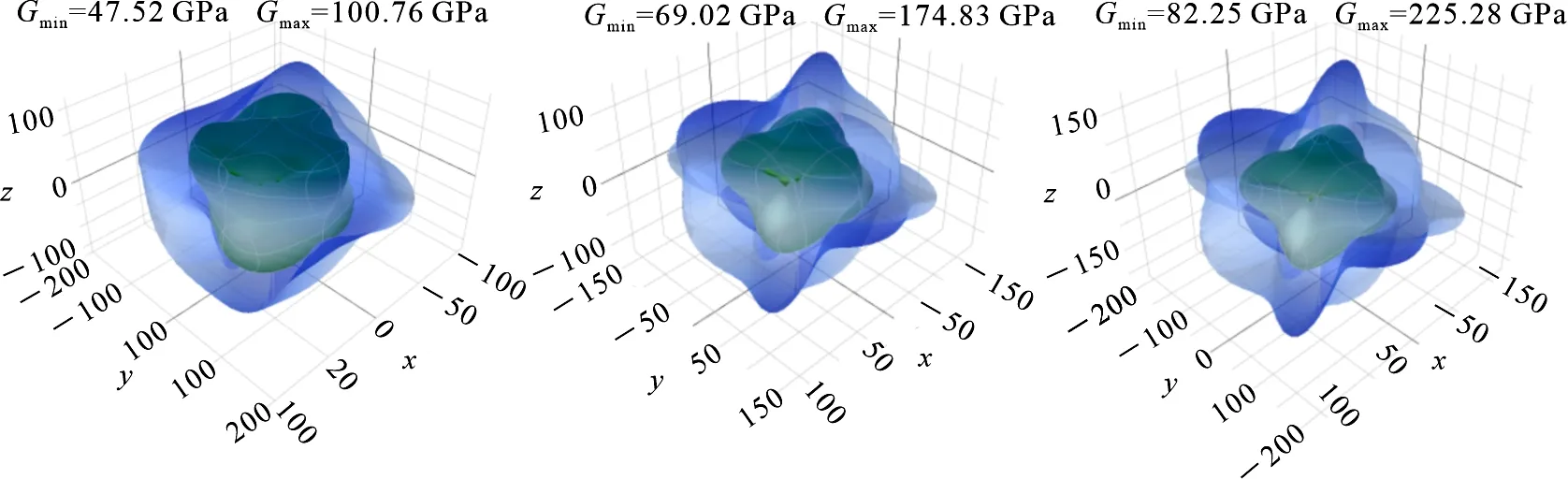
图6 菱镁矿剪切模量G的三维空间分布

图7 菱镁矿杨氏模量E的三维空间分布

2.4 声速各向异性

由于菱镁矿具有弹性各向异性，其纵向(vl)、横向(vt)和平均(vm)弹性波速度可以根据体积模量B、剪切模量G和密度ρ得到[33]

晶体的纯横向和纵向模式的速度可通过单晶弹性常数得到．菱形晶体的纯横模和纵模波速只在[100]和[001]方向．相应方向的声速计算如下:

在[100]=[010]方向,

在[001]方向,

菱镁矿的弹性波速度和各向异性如图8所示．图8a表明，在研究的压力范围内，计算的弹性波速度与前面的实验结果[6]符合地很好，纵波的传播速度vl比横波的传播速度vt快．从图8(b-c)可以看出，纵波速度分别在[100]和[001]方向上最慢和最快．最快的横波在[100]方向，对应于(即沿[010]方向极化)，而最慢的横波沿[001]方向传播，与较小的c44值一致(即分别沿[100]、[010]和[001]方向极化)．由于菱镁矿的弹性波速接近镁橄榄石的弹性波速，因此，菱镁矿对碳酸化橄榄岩和榴辉岩的弹性波速影响不大，上地幔中菱镁矿的存在可能难以被地震探测到[6]．在深部地幔中，菱镁矿的弹性波速度远低于主要候选矿物的弹性波速度[34]．因此，过渡带和下地幔中菱镁矿的富集可能会产生地震可探测的低速带．过渡带底部菱镁矿的富集可以解释初步参考地球模型中过渡带底部异常低的密度和速度梯度[35]．

a.各向同性的弹性波速;b.沿[100]方向传播的弹性波速;c.沿[001]方向传播的弹性波速;圆点表示Yang等的实验值[6]．

3 结束语

由于菱镁矿的高压物理性质对于理解深层碳循环非常重要．文中利用基于密度泛函理论的第一性原理计算，研究了高压下菱镁矿的结构参数、状态方程、弹性常数和弹性模量、弹性声速及各向异性，计算结果与之前的实验和理论结果非常吻合．弹性模量的结果表明菱镁矿的弹性各向异性随压强的增大而增大．纵波的传播速度比横波的传播速度快，纵波速度分别在[100]和[001]方向上最慢和最快．最快的横波在[100]方向，而最慢的横波沿[001]方向传播．正如文献[7]所讨论的，菱镁矿的弹性各向异性远大于地幔中主要矿物的弹性各向异性，其局部富集为过渡带的大局部各向异性提供了新的解释．