反平面波在一维液体饱和多孔声子晶体中的传播特性
张书燕,王艳锋
(1.北京交通大学 土木建筑工程学院,北京 100044;2.天津大学 机械工程学院,天津 300350)
声子晶体[1]是空间周期排列的人工复合材料,其独特特征是产生带隙[2-3],在带隙内弹性波的传播会受到抑制。带隙有两种产生机制:Bragg散射和局域共振[4]。基于带隙特性,Thota等[5]利用一种圆柱夹杂物和折纸结构设计了可重构的声屏障,它可以有效的屏蔽交通噪音;Yoo等[6]利用平面柔性声子晶体实现了小单元在低频域的完美吸声;Dong等[7]利用拓扑优化设计了窄频声子晶体滤波器;Brule等[8]用试验的方法验证了在土体里面插入周期性的材料可以屏蔽地震波。此外,还可通过引入线缺陷设计波导[9],使弹性波沿着缺陷传播。
尽管声子晶体的研究已经受到许多学者的关注,但已有研究大都考虑单相介质,较少涉及两相或多相介质。实际上液体饱和多孔介质(两相介质)也是很常见的材料。探索波在多孔介质中的传播对土木工程和地震工程等领域起到重要的理论指导[10-11]。近年来,一些研究者对弹性波在液体饱和多孔声子晶体中的传播进行了研究。Weisser等[12]计算了具有周期性共振夹杂多孔弹性层的声响应;Alevizaki等[13]将多层散射方法推广到浸没在流体介质的孔隙弹性球的声子晶体;Wang等[14-15]研究了纵波和面内混合模态在一维和二维液体饱和多孔声子晶体中的传播特性;Meng等[16-18]分析了饱和土中放置多排混凝土桩对弹性波的减振效果;徐长节等[19]研究了饱和土夹水混凝土混合式屏障对弹性波隔振效果。Zhang等[20]研究了弹性波在部分开口界面一维液体饱和多孔声子晶体中的波动特性。
以上研究主要关注纵波或面内混合模态在液体饱和多孔声子晶体中的传播,并未涉及反平面波。因此本文重点关注反平面波在一维层状液体饱和多孔声子晶体中的传播特性。首先利用传递矩阵方法计算了反平面波的复能带结构;然后用刚度矩阵法计算了声子晶体的传输谱;最后分析了液体黏性、孔隙率和材料组分比对反平面波传播特性的影响。这些结果为液体饱和多孔材料的实际应用提供理论参考。
1 计算模型
考虑一维层状由n个单细胞组成的声子晶体,每个单胞有两个子层,分别由两种不同的液体饱和多孔介质A和B组成,单胞的长度可以表示为a=a1+a2,其中a1和a2分别为A和B两个子层的长度,如图1所示。本文考虑反平面波以角度θ0∈(0,π/2)入射声子晶体。
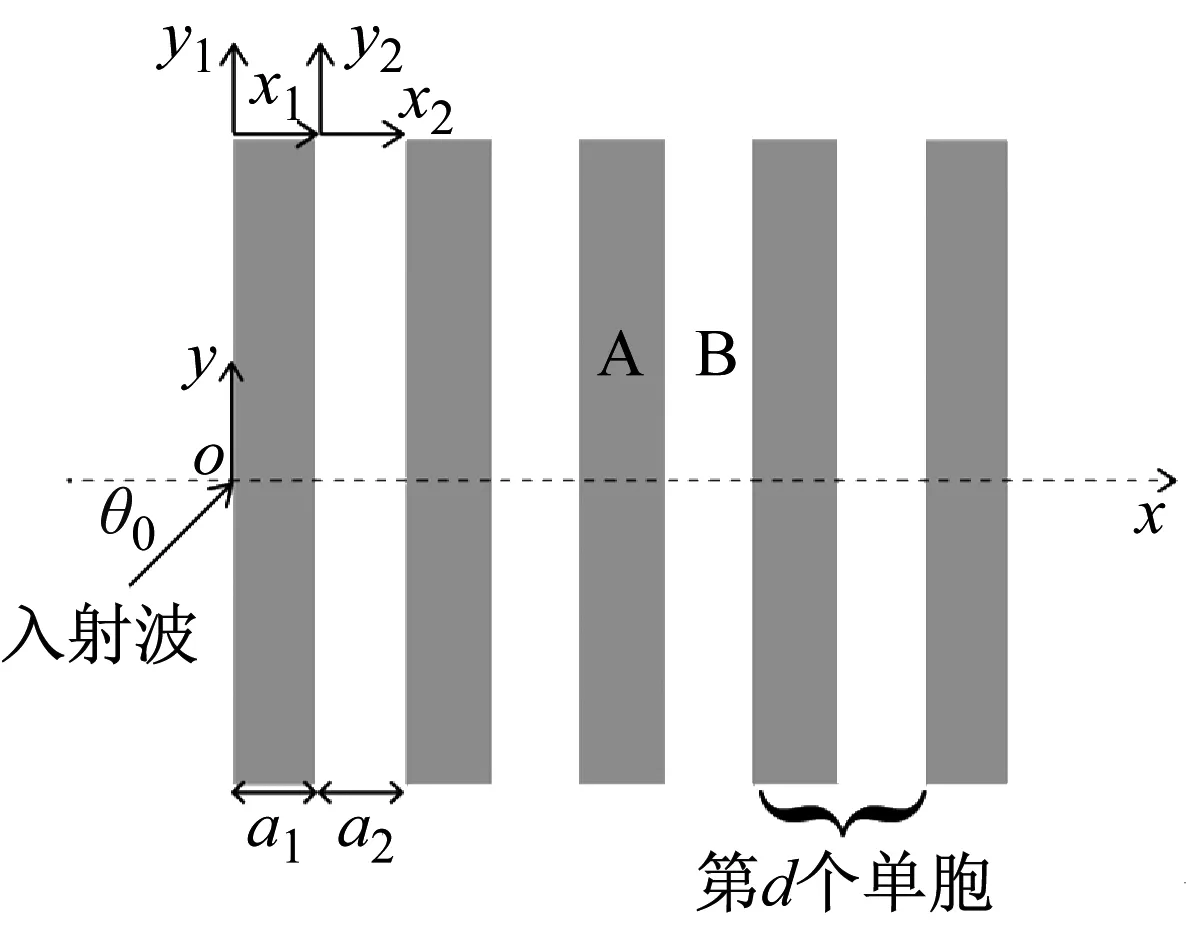
图1 一维液体饱和多孔声子晶体示意图
2 反平面波波动方程的求解
根据Wang等的研究,一维液体饱和多孔介质反平面波的波动方程可以写为
(1)

(2)

对于简谐波,反平面波的位移场可以假设为
(3)

将式(3)代入式(1)得
(4)
若式(4)存在非零解,则相应的系数为零,即
(5)
求解式(5)可得
(6)
这里正值表示波的传波方向,正值表示x方向,负值表示x负向。
利用叠加原理,可以得到位移的通解
(7)
(8)

3 传递矩阵
对于一维声子晶体,传递矩阵法计算能带结构和传输,是常用的方法[21]。传递矩阵法是利用界面位移、应力等连续性条件,得到两个相邻单胞的传递矩阵;进而通过引入Bloch理论求解特征值问题得到能带结构。
假设第d个单胞的状态向量为V=[uz,σxz]T。根据位移和应力的通解,第j子层左右两个界面的状态向量可以表示为
(9)

在第d个单胞子层间的界面以及第d-1和第d个单胞的界面处,状态向量应保持连续
(10)
将式(9)代入式(10)可得
(11)

根据Bloch定理,状态向量有如下关系
(12)
式中,kx为Bloch波矢在x方向的分量。联立式(11)和式(12)可以得到
(13)
从式(13)可得到标准的特征值问题
|T-eikxaI|=0
(14)
式中,I为2×2的单位矩阵。任意给定一个频率,复能带结构可以通过求解方程式(14)得到。
4 刚度矩阵
当声子晶体的层数较多时,用传递矩阵法计算位移响应的解是不稳定的[22]。因此一些研究者提出了稳定的求解方法,如刚度矩阵法[23]和散射矩阵法[24-25]。本文利用刚度矩阵法计算结构的透射系数。
假设声子晶体两侧是两个半无限大均匀结构(液体饱和多孔介质A),反平面波从左侧半空间以角度θ0入射到声子晶体中,那么入射半空间的波场为
(15)

(16)

(17)
式中,σ0=τxz0,u0=ux0,和us=uxs,刚度矩阵KR详见附录B。将式(15)和式(16)代入式(17)可以得到
(18)

5 数值结果和讨论
已有研究表明,反平面波斜入射和垂直入射的结果在低频时基本一致[26],因此本文只分析反平面波垂直入射(θ0=0)时液体饱和多孔声子晶体的波动特性。令上述推导中的ky=0即可得到垂直入射时的传递矩阵和刚度矩阵。本文中材料A为饱和土(a1=1.3 m),B为混凝土(a2=0.7 m)。其他相关材料参数参考Wang等的研究,在本文计算中αj(∞)=1.02。首先考虑无黏性液体饱和多孔声子晶体,计算的复能带实部如图2(a)所示。图中横坐标为归一化波数ka/(2π),纵坐标为归一化频率fa。复能带的虚部,如图2(b)所示。计算50个单胞的声子晶体得到的传输谱,如图2(c)所示。从图2可知,在考虑频率范围内,反平面波有两个Bragg带隙,传输结果与能带结果吻合较好。

(a)Re(ka/2π)
接下来考虑液体黏性对反平面波传播特性的影响,结果如图3所示。作为比较,图中虚线是无黏性的结果。从图3可知,当引入黏性后(η=1×10-6Pa·s),复能带的实部在边界处由尖角变为光滑,通带的虚部值变大,带隙内对应的虚部几乎没有变化。因此,反平面波在通带内的传输减弱,带隙内的衰减几乎没有发生改变。当黏度系数增大到η=1×10-5Pa·s时,上述现象变得更加明显。然而,当黏度系数增大到η=1×10-3Pa·s时,在整个频率范围内反平面波的虚部变小、衰减减弱,复能带的实部在布里渊的边界由光滑又变为尖角。这和快纵波随黏性的变化是一致的。这个现象可以来利用泰勒展开式来解释,首先将ω(k)在复指数k的区域边界k0=π/d处进行泰勒展开[27],即

(a)Re(ka/2π)
Δω=ω(k)-ω(k0)≈ζRe((Δk)2)=
ζ(g2-h2)
(19)
式中:ζ为一个与能带二阶导数有关的常量;Δk=g+ih。对于相同的Δω>0和不同的黏度,能带的衰减是先增大后减小的,并且其相应的虚部也是先增大后减小的,式(19)中的h和g也是有着相同的变化。所以随着黏性系数的增大布里渊边界处尖角先变光滑再变尖锐。
不同孔隙率下液体饱和多孔声子晶体中反平面波的复能带实部、复能带虚部、传输谱以及带隙上下边界位置和带隙宽度变化,如图4所示。为了做对比,图4还给出了孔隙率φ=0(单相介质)的复能带和传输,如虚线所示,第一条带隙和第二条带隙的简约频率范围分别为[624,754]和[1 286,1 490]。与单相介质的结果相比,当孔隙率增大到φ=0.1时,两条带隙上下边界向上移动,带隙内对应的最大虚部增大并且相应的衰减增强,从图4(d)可知,此时带隙也稍微变宽。这是因为质量密度比能影响带隙产生[28],并且当基体和散射体密度相差较大时更容易产生带隙[29]。多孔介质A孔隙率的增大会导致其平均密度减小,因此多孔介质A与多孔介质B的平均密度之差也变大。当孔隙率增大到φ=0.3和φ=0.4时,上述现象变得更加明显。与快纵波不同,在高频范围内反平面波通带对应的虚部值为零,这是因为反平面波的波动方程与流体压力无关,即反平面波和慢纵波之间不存在相互作用。从图4(d)可知,随着孔隙率的增大,带隙边界向上移动与快纵波正好相反,带隙逐渐变宽。

(a)Re(ka/2π)
当单胞长度不变时,不同组分比(Q=a1/a2)对反平面波传播特性的影响。不同组分比的复能带和传输,如图5所示。当组分比较大时Q=9/1,第一条布拉格带隙和第二条布拉格带隙的简约频率范围为[644,686]和[1 290,1 380]。当组分比稍微变小Q=13/7时,两条带隙增大,带隙内虚部值和衰减也显著增大。当组分比减小到Q=3/7时,反平面波的相速度增大,第一条带隙变得更宽,带隙内的衰减进一步增强。但是第二条带隙变窄,带隙内的衰减减弱。带隙的这种变化是由于布拉格散射引起的,因此可以估计出带隙的中心频率。带隙中心频率可以用下式来估计[30]

(a)Re(ka/2π)
(20)
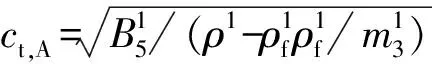

表1 不同组分比下带隙的数值中心频率和估算中心频率
6 结 论
本文基于Biot理论和Bloch理论,研究了反平面波在一维液体饱和多孔声子晶体中的传播特性。分别利用传递矩阵法和刚度矩阵法计算了复能带结构和传输谱。分析了黏度系数、孔隙率和材料组组分比对反平面波传播特性的影响,得到如下结论:
(1)引入黏性后,反平面波的虚部先增大后减小,相应的衰减先增强后减弱,复能带的实部在布里渊区边界处先变光滑后再变成尖角。
(2)随着孔隙率的增大,A,B两种液体饱和多孔介质的密度差变大,带隙变宽,同时带隙边界向上移动。与快纵波不同的是,由于反平面波和慢纵波不存在相互作用,因此反平面波高频通带对应的虚部没有发生改变。
(3)随着组分比的减小,两条带隙变宽,带隙内的衰减增强,当组分比减小到一定值后,第二条带隙变窄,并且衰减变弱。估算的带隙中心频率值和数值结果基本一致。
附录A
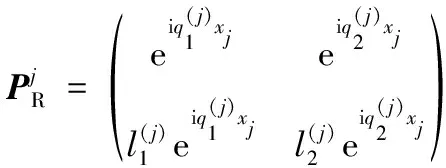
(A.1)
附录B
参考文献[31],假设一个单胞内两个子层的刚度矩阵分别为KA和KB,第一子层左侧界面、两子层界面处以及第二子层右侧界面的广义应力和位移分别[σ1,u1]T、[σ2,u2]T和[σ3,u3]T。根据本构方程有

(B.1)
式中,KA和KB为2×2的矩阵,表达式分别为
(B.2)
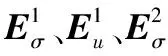
通过消除式(B.1)的σ2和u2,可以得到单胞的局部刚度矩阵
(B.3)
考虑声子晶体由r个相同的单胞组成,假设前r-1个单胞的整体刚度矩阵为KR-1,第r个单胞的局部刚度矩阵为Kr,根据方程(B3)可以得到含r个单胞的声子晶体全局刚度矩阵的递推公式
KR=
(B.4)
附录C
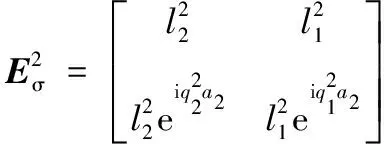
(C.1)

