Nonreciprocal two-photon transmission and statistics in a chiral waveguide QED system

Lei Wang(王磊), Zhen Yi(伊珍), Li-Hui Sun(孙利辉), and Wen-Ju Gu(谷文举)

School of Physics and Optoelectronic Engineering,Yangtze University,Jingzhou 434023,China

Keywords: chiral waveguide QED,nonreciprocal transmissions,nonreciprocal correlations

1. Introduction

Recently,intensive attention has been paid to exploration of chiral interfaces to tailor atom–light interactions for important applications in quantum devices and quantum information techniques.[1–4]The novel effect arises from the peculiar polarization exhibited by strongly and transversely confined optical fields in nano-photonic structures such as nanofibers and photonic crystal waveguides(PCWs).[5–8]The transverse confinement naturally leads to dependence of polarization properties of light on the propagation direction, which is a manifestation of optical spin–orbit coupling.[9]As a result,the interaction between light and a quantum emitter (QE) depends on propagation direction of light and polarization of the transition dipole moment of the QE,in contrast to the identical interactions between the QE and photons of the either two propagation directions in regular waveguides. In practice, chiral interface facilitates the realization of optical nonreciprocity.

Optical nonreciprocity means that the properties of transmitted fields become asymmetry when exchanging the positions of source and detector.[10]Various nonreciprocal phenomena have been intensively investigated, including nonreciprocal transmission and amplification,[11–16]nonreciprocal (unconventional) photon blockade,[17–20]nonreciprocal signal routing,[21–23]and nonreciprocal quantum entanglement,[24–26]etc. The strategies for realization of nonreciprocity cover magneto-optical materials in conjunction with a magnetic field,[27,28]time modulation of the optical properties,[29]optical nonlinearity,[13,30,31]and synthetic magnetism,[32]etc.In addition,nonreciprocity based on a new paradigm referred to as “chiral quantum optics” has been investigated, where the nonreciprocal behavior is controllable by the spin state of the QE.[33–36]Furthermore, the scalable quantum techniques involving miniaturization and fabrication problems in nanophotonic waveguide systems have been assessed, in which chiral coupling is considered to be wellcharacterized and robust,and has potential implementation in a range of applications.[37–39]

Nonreciprocal phenomena in chiral systems are mainly focused on the single-photon level,and the properties at twoor multi-photon levels are less studied. The two-photon transport has been addressed in regular waveguide systems using the several interrelated theoretical techniques such as multiparticle scattering theory,[40–44]input-output formalism,[45–48]approaches based on Lippmann–Schwinger equations[49]and Lehmann–Symanzik–Zimmermann reduction.[50]Scattering theory is a common framework to study scattering of waves and particles in real space within the Schr¨ongdinger picture,and applied in different branches of physics. The input-output formalism was mainly developed for understanding lightmatter interaction in momentum space based on the Heisenberg picture,[51]and its extension to scattering of multiple photons by multiple interacting and noninteracting emitters in a 1D continuum has been investigated.[48,52]In theory,the bidirectional case in no matter the regular or chiral waveguides can be treated through generalizing the case of propagation in a single direction.[52]Therefore, the approach taken in regular waveguide systems can be extended to study the two- or multi-photon chiral waveguide systems.

Here we follow the approach of scattering wave function in a real-space formalism to construct scattering matrixes via imposing open boundary conditions and the incoming plane wave functions, and to study the nonreciprocal two-photon transmission and statistics in a chiral waveguide system. Via introducing the bright and dark optical modes,the bright mode effectively couples to the QE while the dark mode is decoupled, and the system reduces to the case of an effective single direction of propagation. To investigate the two-photon transmission, it is necessary to analyze single-photon transmission firstly, where the nonreciprocity is induced by the joint effects of chiral coupling and atomic dissipation in the weak coupling regime. In the strong coupling regime,the effect of atomic dissipation becomes ignorable, and the nonreciprocity disappears. For the two-photon case, there are two ways for photons going through the QE.One is to pass by the QE independently as plane waves and gain a phase factor,and the other is to bind together to form a bound state. Planewave term is similar to the single-photon transmission. Due to the different interactions in two directions,left-propagating photons hardly form the bound state in which transmission is mainly determined by the plane-wave term,while bound state formed by right-propagating photons further alters the transmission probability. In addition,the second-order correlations of transmitted photons in the two directions are discussed. For the right-propagating photons,the destructive interference between plane wave and bound state leads to the significant antibunching in the weak coupling regime,and the effective formation of bound state leads to the strongest bunching at the intermediate coupling. For the left-propagating photons, the negligible interaction hardly changes the statistics of the input coherent state.

The paper is organized as follows. In Section 2, the chiral waveguide QED system is introduced, and the nonreciprocal transmissions of single-and two-photon Fock states are analyzed in Sections 3 and 4. In Section 5, the nonreciprocal second-order correlations of transmitted photons are discussed,and lastly the conclusion is drawn.

2. Chiral coupling between the light and QE

Fig. 1. Schematic of chiral photons in evanescent fields coupled to a σ+-polarized emitter. Polarization properties of the evanescent light field that surrounds an optical nanofiber are: a y-polarized light field that propagates in the right(+x)direction is mainly σ+polarized in the(z=0)plane. If it propagates in the left(-x)direction,it is mainly σpolarized.

Now it is necessary to introduce the bright and dark optical modes

where the bright mode effectively couples to QE with strengthgB, while the dark mode is free from the interaction. Thus,the system becomes an effective light-QE interaction in one direction of propagation. For simplicity, we will takeυgas 1 hereafter.

3. Nonreciprocal transmissions of single-photon Fock state

Before the discussion of two-photon transport, we first consider the single-photon scattering process,which is necessary to construct the two-photon scattering matrix later. The stationary one-excitation state in the bright-state subspace is given by

withΓj=g2j. In Fig. 2 we present the nonreciprocal transmissions of right- and left-propagating single-photon Fock states as functions ofΓRunder the condition of chiral couplingΓL=0.1ΓRand atomic decay rateγ=0.2. The nonreciprocal behavior is most obvious atΓR=0.2,where the transmission probability of right-propagating input state is much smaller than that of left-propagating input state. The nonreciprocal single-photon transmission can be explained from the perspective of mode conversion, where the photonic mode is absorbed by the QE and then re-emitted into the waveguide or the environment.[59]The transmission amplitudes of rightand left-propagating input states are

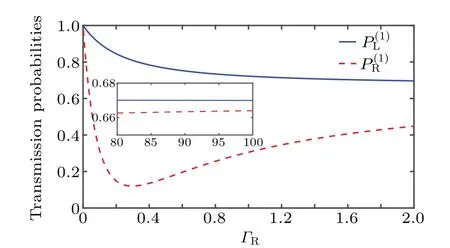
Fig.2. Nonreciprocal single-photon transmission probabilities andfor the right-and left-propagating input Fock states as functions of ΓR. Incident field is on resonance with the QE(k0=ε),the atomic dissipation is γ=0.2,chiral interactions fulfill ΓL=0.1ΓR,and the spectral width is Δ =0.1.

4. Nonreciprocal transmissions of two-photon Fock state

Fig. 3. The x2 ＞x1 region is dissected into three subregions: (I)0 ＞x2 ＞x1, (II) x2 ＞0 ＞x1, (III) x2 ＞x1 ＞0, due to interactions at the coordinate axes x1=0 and x2=0.

andQ=(Q1,Q2)is permutations of(1,2)required to account for the bosonic symmetry of the wave function. Conceptually,two photons have two ways of going through the QE.One is to pass by the QE independently as plane waves and gain a phase factor, which is indicated by the first term off2(x1,x2). The other way is to bind together and form a bound state, which is indicated by the second term. The formation of the bound state can be viewed as a result of stimulated emission: the first photon excites the QE and the passing of the second photon stimulates emission of the first photon into the same state,hence producing the bound state. The two-photon bound state must be included to guarantee the completeness of the basis,as previous discussions by Shen and Fan.[42,43]

The two-photonSmatrix connects the freely incoming and outgoing photonic states (away from the QE), which is defined as

which is explicitly expressed in the form

Fig. 4. Two-photon transmission probabilities and of rightand left-propagating input states as functions of ΓR. (a)Probability for the right-propagating two-photon Fock state.(b)Probability for the leftpropagating two-photon Fock state. The label PW refers to the contribution from the plane-wave term,while BS refers to all the other contributions involving bound-state terms. Incident photons are on resonance with the QE(k0=ε),the atomic dissipation rate is γ=0.2,chiral interactions fulfill ΓL=0.1ΓR,and Δ =0.1.

5. Nonreciprocal second-order correlations of transmitted photons

Now we turn to the statistical properties of transmitted photons to show the nonreciprocal photon-photon correlations induced by the chiral interactions. Explicitly,we calculate the second-order correlation function for scattering of continuousmode coherent states,which is defined by[58]

Particularly,we consider the mean photon number ¯n ≤1.In this case, the distribution ofn ≥3 number states is much lower than that ofn=2 number state. Therefore,it is appropriate to truncate to two-photon scattering of the continuousmode coherent input state. We study the second-order correlation function of the transmitted field for the right-propagating input state that is defined as

Fig.5. Second-order correlation functionsnd of transmitted photons as functions of ΓR. The curves of correlations vary with different ΓL/ΓR, where ΓL/ΓR =0.1 (black-solid line), ΓL/ΓR =0.5 (red dash-dotted line),ΓL/ΓR =1 (blue-dashed line). The other parameters are k0=ε,γ =0.2,and Δ =0.1.

6. Conclusions

In summary, we have studied the nonreciprocal singleand two-photon transmissions, and second-order correlations in the chiral waveguide QED system. For the single-photon transmission, the nonreciprocity is induced by the effects of chiral coupling and atomic dissipation, which is the most obvious atΓR=γ. In the strong coupling regime, the effect of atomic dissipation becomes ignorable, and the nonreciprocity almost vanishes. For the two-photon case, the transmission is contributed by plane-wave and bound-state terms. The plane-wave term means that photons pass by the QE independently as plane waves and gain a phase factor, while boundstate term means that photons bind together and form a bound state. Plane wave behaves similarly to the single-photon transmission. However, due to the different interactions in two directions, left-propagating photons hardly form the bound state, while bound state of right-propagating photons alters the transmission probability further. Moreover, the interference between plane wave and bound state modifies the statistics of transmitted photons. The destructive interference leads to strong antibunching in the weak coupling regime,and constructive interference leads to strong bunching in the intermediate coupling regime which is consistent to the effective formation of bound state. In the left direction, the negligible interaction between photons and QE hardly changes the statistics of the input coherent state.

Acknowledgement

This work was supported by the National Natural Science Foundation of China(Grant No.11704045).