Noncollinear phase-matching geometries in ultra-broadband quasi-parametric amplification

Ji Wang(王佶) Yanqing Zheng(郑燕青) and Yunlin Chen(陈云琳)

1Institute of Applied Mic-Nano Materials,School of Science,Beijing Jiaotong University,Beijing 100044,China

2School of Materials Science and Chemical Engineering,Ningbo University,Ningbo 315211,China

Keywords: quasi-parametric amplification,noncollinear phase-matching geometry,nonlinear optics,ultrafast optics

1. Introduction

Ultra-short high-intensity lasers based on chirped pulse amplification (CPA) technique have been widely studied. As a result, 10-petawatt-class lasers have been achieved, such as the Shanghai super-intense ultrafast laser facility (SULF,339 J, 21 fs),[1]the European Extreme Light Infrastructure(ELI, 250 J, 22.5 fs, 1/60 Hz) 10 PW facilities,[2]and the Apollon (150 J, 15 fs, 1/60 Hz) 10 PW facility.[3]Several PW-class lasers based on optical parametric chirped-pulse amplification (OPCPA) have been developed.[4–6]OPCPA has great potential in the next-generation hundred-petawatt class lasers because of its high gain, high contrast, and large gain bandwidth.[4]A picosecond-pumped OPCPA can provide a larger bandwidth than a nanosecond-pumped OPCPA because a thinner crystal can be applied with a larger pump intensity.[7]In a nanosecond-pumped OPCPA, the pump intensity is limited because of the damage threshold of nonlinear crystals.[8]Nanosecond-pumped OPCPA is widely used in high-power laser facilities,[4–6,9]whereas its bandwidth has been limited. Recently,a new scheme called quasi-parametric chirped pulse amplification (QPCPA) shows great potential in broadband amplification. It can amplify the signal to its theoretical conversion efficiency limit even with a large phase mismatch.[10,11]Here the theoretical conversion efficiency limit means that the conversion efficiency can reach the limit only constrained by the conservation of energy. The high tolerance towards the walk-off and thermal dephasing in QPCPA within a long propagation length is also discovered.[12]The difference between QPCPA and OPCPA is that the nonlinear crystal used in QPCPA has idler absorption. In OPCPA,the conversion efficiency is limited by the back conversion when there are spatial and temporal distributions.[10]However,this limitation does not exist in QPCPA because the idler absorption suppresses the back conversion process. Up to date,the signal spectrum together with the amplification process in QPCPA is not fully investigated yet.In this article,we describe the signal evolution process in QPCPA to show the origin of the stability towards phase mismatch and the origin of the spectral phase in QPCPA which is different from the spectral phase in OPCPA.We have also investigated the gain factor and the signal spectrum to show its potential in broadband amplification at a limited pump intensity. The numerical simulation results demonstrate that the pulse duration can achieve 7.92 fs at a pump intensity of 5 GW/cm2in a doped-YCa4O(BO3)3(YCOB)crystal by applying a novel triple-wavelength phasematching geometry.

2. Description of the signal evolution in QPCPA

Firstly, we analyze the amplification process by a set of simplified three-wave-mixing equations:

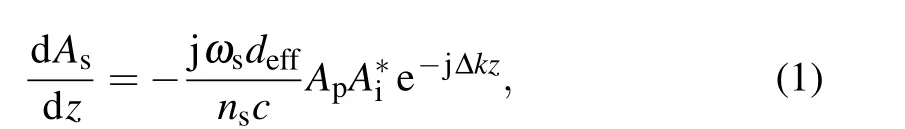
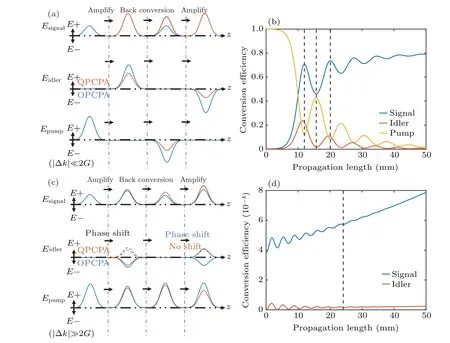
Fig. 1. The description of signal amplification under extreme conditions to show the two different back conversion mechanisms. (a) The description to the amplification process when |Δk|≪2G. (b) The corresponding intensity changes of signal, idler and pump in QPCPA calculated with an initial gain factor of 450 m-1, Δk=200 m-1, Ip/Is =3200 and α =200 m-1 with fourth order super-Gaussian profiles.(c)The description of signal amplification when|Δk|≫2G. (d)The corresponding intensity changes in QPCPA,which is calculated with an initial gain factor of 450 m-1,Δk=2000 m-1,Ip/Is=3200 and α =200 m-1.

As shown in Figs. 1(a) and 1(b), the two mechanisms dominate when|Δk|≫2Gand|Δk|≪2G,respectively.When|Δk|＜2G, the signal can be similarly amplified in both OPCPA and QPCPA.For a specific condition Δk=0,the signal can be continually amplified until the pump is fully depleted. When the phase mismatch is much smaller than the gain factor and ignore the temporal and spatial distributions of the pump and the signal, the pump can be fully depleted or nearly depleted. Then a new pump field is generated by the signal and idler with an electric field direction opposite to the origin pump, which is equivalent to aπphase shift on the pump, as shown in Fig. 1(a). The newly generated pump gradually depletes the signal and idler and makes the signal intensity in OPCPA changing periodically. In QPCPA,the idler is partially absorbed during propagation. When the pump converts to signal and idler,it obeys the law of conservation of energy,which is also called the Manley–Rowe relations.Thus,if the temporal and spatial distributions are ignored,the intensity of the signal without phase mismatch can eventually reach the theoretical conversion efficiency limit no matter whether there is idler absorption or not. During the back conversion, the signal decreases until the idler fully converts to pump, which also obeys the Manley–Rowe relations. Hence,the remaining signal intensity in QPCPA is larger than in OPCPA,while the converted pump intensity in QPCPA is less than in OPCPA.After a long-distance propagation,both the idler and the pump are negligible while the signal is kept at the theoretical conversion efficiency limit,as shown in Fig.1(b).

The relationship between the phase mismatch and the gain factor finally becomes|Δk|＞2Gbecause the pump is gradually consumed with the amplification process. We shall consider the two kinds of processes that happen in the threewave mixing process after the signal and the pump produces a new idler component with an envelope dAiin a very short distance dz, and we temporally ignore the existed idler components. The newly generated idler component converts into the signal within a very short distance,or it propagates a long distancezbefore it converts to the signal. The envelope of the newly generated idler component carries a phaseφ(ApA*s)-Δkz0,z0is the position where the new idler component is generated. In the first case,the immediately generated new signal component carries a phaseφ(ApA*pAs)=φ(As), which is the same as the existing signal component. In the second case,the idler propagates a lengthzand then converts to signal at the positionz1=z0+z. In this article,we call these accumulated idler components‘the formerly generated idler’,and call the accumulated signal components (‘the formerly generated signal’). The envelope of the formerly generated idler component generated atz0carries a phaseφ(ApA*s)-Δkz0when it propagates toz1(notice thatAs,AiandApdo not carry the phase produced by the propagation, and Δkzterm carries this phase component is carried). The envelope of the signal component converted by the formerly generated idler component carries a phaseφ(ApA*pAs)-Δk(z1-z0)=φ(As)-Δkz. We want to discuss the condition|Δkz|＞π, which leads to the back conversion.In OPCPA,the intensity of the amplified signal is nearly the same as the intensity of the formerly generated signal within the distancelefflimited by the parametric bandwidthleff＜π/|Δk|. Then, the phase difference between the newly generated signal and the formerly generated signal gradually becomes larger thanπ/2. When the phase difference is larger thanπ/2, the idler and the signal back convert to the pump,and therefore the signal cannot be amplified. We name the phase of the signal,the idler,and the pump asφs,φi,andφp, respectively. The phase mismatch Δkzhas been considered inφs,i,p. Presume that the initial phase of the signal,the idler and the pump are the same,then when the phase mismatch is in the range of 0＜|φs+φi-φp|＜π/2,the signal and the idler is amplified together. When the phase mismatch is in the range ofπ/2＜|φs+φi-φp|＜π,the difference between the phase of formerly generated signal (idler) and the phase of newly generated signal(idler)is larger thanπ/2. Then the signal and the idler continually back convert to the pump until the later generated idler(signal)completely cancel out the formerly generated idler(signal). The difference between the phase of the newly generated signal and the phase of the existing signalφp-φi-φsvaries periodically aroundπ/2,and the signal intensity varies with the same period.

In QPCPA, when the phase mismatch is in the range ofπ/2＜|φs+φi-φp|＜π, the phase mismatch of the existing signal and idler components is large,and the existing idler components are gradually absorbed. The phase mismatch of the newly generated signal and idler components is relatively smaller. The proportion of subsequently generated idler increases with the enhancement of the absorption of the idler,and the back conversion is inhibited. The amplification is suppressed in the next 0＜|φs+φi-φp|＜π/2 interval because the idler generated in the previousπ/2＜|φs+φi-φp|＜πinterval is not fully depleted. Finally,due to the idler absorption,the later generated idler intensity ratio to the existing idler intensity remains a constant greater than 1 in a|Δk|=2πperiod. The corresponding phase differenceφs+φi-φpremains at a value less thanπ/2, and the back conversion gradually disappears. The signal’s withdrawal in QPCPA is less than that in OPCPA, ensuring the signal increases. When the signal intensity is increasing, the phase differenceφs+φi-φpis further reduced and accelerates the amplification to exponential growth,as shown in Fig.1(c). The exponential growth speed,i.e.,the effective gain factor(the gain factor considering the phase mismatch and the absorption),depends on the ratio of the later generated idler and the existing idler. Therefore the effective gain factor increases with the absorption coefficient until the absorption displays more inhibition than promotion. This phenomenon has also been found and named the‘self-locked phase’.[11]This effect ensures that every component in the signal can be amplified to its theoretical conversion efficiency limit in a long enough nonlinear crystal, even if there is a large phase mismatch. An extreme situation is shown in Fig.1(d),which shows the back conversion gradually disappears in QPCPA even if there is a large phase mismatch Δk=2000 m-1and a short coherence lengthπ/Δk ＜2 mm.

3. Broadband amplification and the phasematching strategy in QPCPA

In a real system,the crystal length is limited. The crystal length required to ensure the conversion efficiency is longer than the crystal length required to maintain the parametric bandwidth in OPCPA.When the effective gain factor is close to zero due to the pump laser depletion,the signal components in the large phase mismatch regions are no longer amplified,as shown in Figs.2(a)and 2(b). Thus,the spectral bandwidth of the amplified signals may be narrower than the seed spectrum in a high efficient nanosecond-pumped OPCPA stage. However,the effective gain factor in the large phase mismatch region does not vanish in QPCPA. This property ensures ultrabroadband amplifications without spectrum narrowing.

Fig. 2. The effective gain factor with the phase mismatch for (a)G=1000 m-1 and(b)G=500 m-1.

Generally, the length of a nonlinear crystal is not unlimited. It is essential to investigate the gain factor in QPCPA and show its potential at limited crystal length. The exact expression of signal can be calculated with Eqs. (1)–(3)when the pump depletion can be ignored, and the coefficient of exponential term ofAsis (-j×Δk/2+(G-(Δk+j×α/2)2/4)1/2-α/4)z. Here the real part of (G-(Δk+j×α/2)2/4)1/2provides the gain and the imaginary part provides the phase, as described in our previous work.[12]When Δk ≈0, the QPCPA gain factor can be expressed as(G2-Δk2/4+α2/16)1/2-α/4,as described in Ref.[11],but this expression is lack of accuracy when Δkis large. When the phase mismatch|Δk|＜2G, the OPCPA effective gain factorGOPCPA=(G2-Δk2/4)1/2is larger than the QPCPA effective gain factorGQPCPA=Re(G-(Δk+j×α/2)2/4)1/2-α/4.When|Δk|≈2G, the OPCPA effective gain factor is close to zero and shows a cutoff of the gain bandwidth. The QPCPA gain factor decreases to about(αG)1/2/2-α/4 and the maximum effective gain factor is 0.3Gatα=2G.When|Δk|＞2G,the OPCPA cannot amplify the signal, and the signal intensity shows periodical oscillation. In contrast,the QPCPA can continually amplify the signal to the theoretical conversion efficiency limit. The results show that in QPCPA, the components with a large phase mismatch|Δk|≈2Gcan be amplified to the theoretical conversion efficiency limit using a crystal 3–4 times longer than the crystal used in OPCPA. In contrast,these components cannot be amplified in OPCPA. The phase mismatch increases rapidly with bandwidth extension so that a long crystal with a large absorption is required to amplify the components where|Δk|＞2G. When the gain factorGdecreases,the QPCPA effective gain factorGQPCPAdecreases more than the factorGso that a longer crystal is required to amplify all possible components in QPCPA.If a QPCPA system is designed to have the same bandwidth as an OPCPA system but suppresses the back conversion,it just requires the absorption to be large enough to ensure that the residual idler is much smaller than the signal. After the pump has been totally converted to signal and idler, the idler continually decreases with a factor-α/4. We presume|Ei|/|Es|=1/e2≈e-α(z-ln(Ep/Es)/G0)/4, whereGis the initial gain factor without pump depletion, so that the required absorption can be expressed asα=8/(z-ln(Ep/Es)/G). For a 50-mm-long crystal with a gain factor of 450 m-1and|Ip|/|Is|～3200,the absorptionαshould be larger than 195 m-1. Suppose that a QPCPA is designed to provide an ultra-broadband amplification, then the maximum absorption should be at least 2G0=900 m-1to support the amplification at the point|Δk|≈2G,which puts forward a higher requirement to the crystal doping.

A large gain factor can easily support an ultrabroadband spectrum in OPCPA or QPCPA towards few-cycle pulses. However, a high gain factor can hardly be achieved at nanosecond scale in the commonly used nonlinear crystals such as BBO (＜1.2 GW/cm2@532 nm, 8 ns),[14]YCOB (7.24 GW/cm2@532 nm, 8.5 ns),[15]or Sm:YCOB(6.41 GW/cm2@532 nm, 8.5 ns)[16]because of the damage threshold. The pump intensity highly limits the bandwidth in nanosecond amplification stages,[6]and affects the pulse duration in petawatt laser facilities. In these crystals,the gain factorGcan hardly achieve 500 m-1, which limits the gain bandwidth in OPCPA. The development of petawatt lasers leads to higher intensities in amplifiers. Strong nonlinear effects in picosecond-pumped amplifiers such as selffocusing may become serious. Moreover, these picosecondpumped amplifiers may require extremely large optics in nextgeneration petawatt lasers. However, nanosecond-pumped amplifiers can avoid these nonlinear effects and reduce the size of optics. Therefore, it is reasonable to discuss the amplification at a limited pump intensity, e.g.,＜5 GW/cm2in YCOB crystals. The noncollinear geometry (noncollinear OPCPA) can achieve a larger bandwidth in OPCPA than the collinear geometry. The noncollinear geometry in OPCPA aims to adjust the first-order derivation of wave-vector mismatch d(Δk)/dω|(ω=ωs)=0 while maintaining the wavevector mismatch at the central wavelength Δk|(ω=ωs)=0.By adjusting the signal wavelength in the system,the residual second-order wave-vector mismatch term becomes zero. The wavevector mismatch becomes the third-order mismatch term and a large bandwidth can be achieved. This scheme is called ultra-broadband OPCPA.[17]The phase-matching bandwidth in ultra-broadband OPCPA can be derived from Ref. [17]when ignoring the pump depletion as

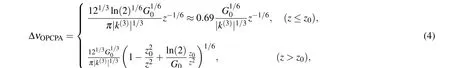
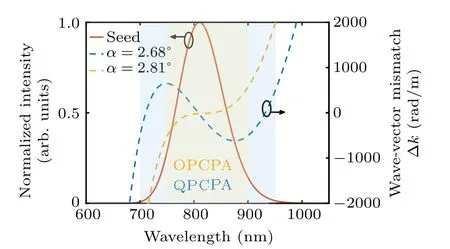
Fig.3.The Gaussian-shaped seed spectrum has a Fourier transform limit(F-T limit) of 10 fs. The triple-wavelength phase-matching QPCPA operates at a noncollinear angle of 2.68°,with a larger bandwidth than in the noncollinear OPCPA (a=2.81°). The noncollinear angles calculated with Eq. (14) use the refractive index of Sm:YCOB. When a=2.81°, GV=169 fs, GVD=-6×103 fs2 and k(3) =-3×105 fs3. When a=2.68°, GV=5×103 fs,GVD=3×103 fs2 and k(3) =-3×105 fs3. See the text for definitions of GV and GVD.

When the maximum acceptable phase mismatch has been determined,the maximum GV of the triple-wavelength phasematching QPCPA is determined by|Δk(ω1)|＜|Δkupper|,and the parametric bandwidth can be solved withωpm=±(6|GV|/|k(3)|)1/2. When the noncollinear angle is away from the broadband condition where the phase mismatch contributed by the GV is larger than the phase mismatch contributed by thek(3), the phase-matching bandwidth is limited by GV:

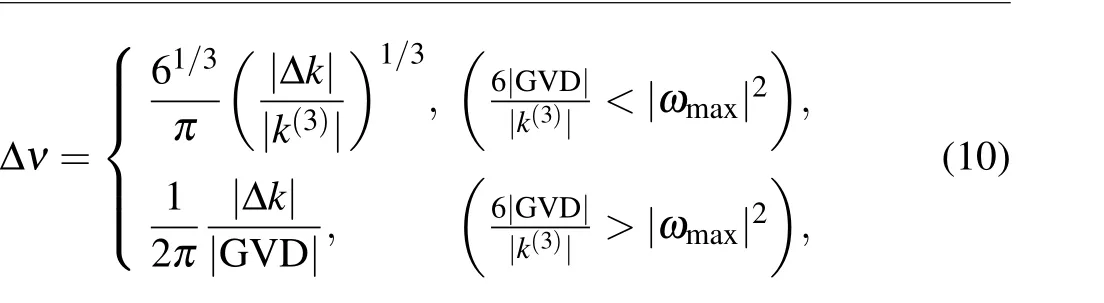
whereωmaxis the largest frequency component in the signal spectrum, the bandwidth decreases rapidly away from the ultra-broadband noncollinear geometry (i.e.,|GVω|≫|k(3)ω3/6| within the signal spectrum). Here we focus on the bandwidth in the ultra-broadband triple-wavelength phasematching geometry, and the corresponding phase-matching bandwidth can be estimated as follows:

Equation (11) shows that a larger gain factor, longer crystal length, and higher signal intensity are helpful to get a larger bandwidth in QPCPA. When QPCPA is operated with the same geometry as an ultra-broadband noncollinear OPCPA,the bandwidth can be solved by

The phase-matching bandwidth can be derived as follows:

The phase-matching bandwidth in ultra-broadband noncollinear phase matching geometry is narrower than the bandwidth in triple-wavelength phase-matching geometry,ΔνQPCPA-NPM≈0.73ΔνQPCPA-TPM.

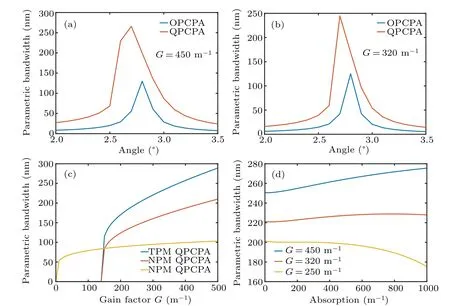
Fig. 4. The parametric bandwidth changes with noncollinear angle when (a) G0 =450 m-1 and (b) G0 =320 m-1. Here, (a) and (b) are calculated with a crystal length of 50 mm for QPCPA and 10 mm for OPCPA, Ip/Is ≈3200 and α =2G. (c) The parametric bandwidth changing with the gain factor when z=50 mm for QPCPA and z=z0 for OPCPA,Ip/Is ≈3200 and α =2G. (d)The parametric bandwidth changing with the absorption when z=50 mm and Ip/Is ≈3200.

Figure 4(c) shows the parametric bandwidth versus the gain factorG. The triple-wavelength phase-matching QPCPA can achieve a bandwidth larger than noncollinear QPCPA and noncollinear OPCPA. Only half of the pump intensity is required in triple-wavelength phase-matching QPCPA in order to get the same bandwidth with noncollinear QPCPA. The bandwidth increasing in QPCPA is limited when the gain factor is large enough because QPCPA cannot amplify the components where signal and idler are overlapped. In the triplewavelength phase-matching scheme,the best noncollinear angle is determined by GV. To simplify the question, we can ignore the changes of GVD andk(3)compared to the change of GV when changing the noncollinear angle (the angle isa) and phase-matching angleθaround Δk|(ω=ωs)=0 and GVD=0. The relationship between GV and noncollinear angleacan be expressed as

whereb= arcsin(ks/ki×sin(a)).ksandkiare the wavevector of the signal and the idler, respectively. When the parametric bandwidth already determines the maximum acceptable phase mismatch atω1, GV can be calculated by Δkmax=±2(1/3)3/2(-6GV/k(3))1/2. And the noncollinear angle can be solved by Eq. (14). The parametric bandwidth changes with the noncollinear angle considering GV, GVD andk(3)are shown in Figs.4(a)and(b). When the gain factor is 450 m-1,the absorption is 900 m-1andIp/Is≈3200 with a 50 mm long crystal, the best noncollinear angle in QPCPA is between 2.6°and 2.7°. When the gain factor is reduced to 320 m-1and the absorption is 640 m-1,the best noncollinear angle is close to 2.7°. The noncollinear angle in OPCPA remains about 2.8°,which does not change with the gain factor.Figure 4(d) shows that a larger absorption coefficient is required to reach the parametric bandwidth maximum with the gain factor increasing,and the absorption required by the maximum parametric bandwidth is approximatelyα=2G.

4. Results and discussion

The triple-wavelength phase-matching QPCPA spectra have been simulated with three-wave mixing equations. In the following simulations, we use the refractive index of Sm:YCOB crystals considering up to the third-order material dispersion and assume ideal absorption spectra:

whereτis the time normalized by the pulse duration of signalts,τ=t/ts;ks,ki,kpare the wave vectors of the signal, the idler and the pump,respectively.

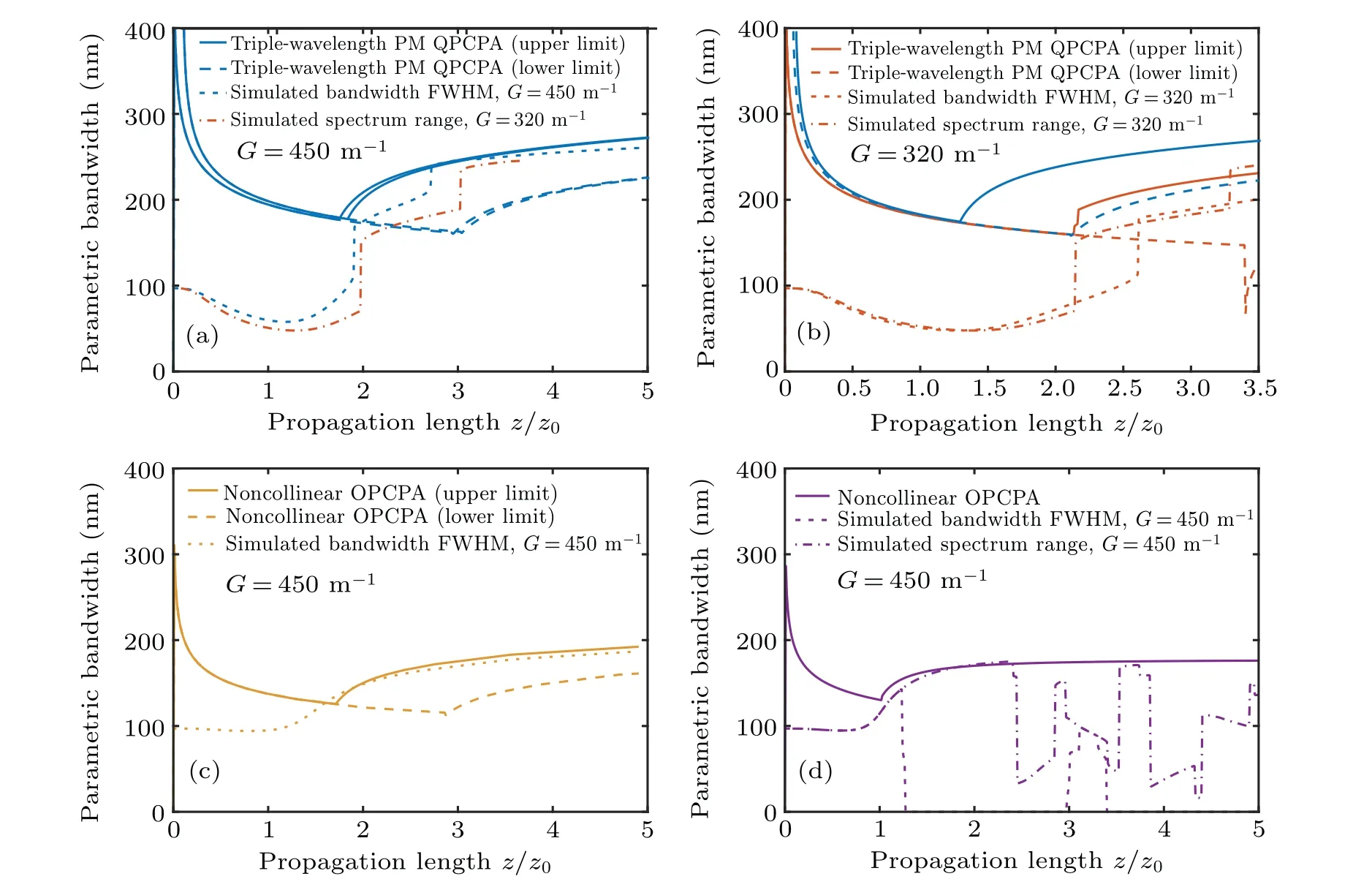
Fig.5.The parametric bandwidth and the simulated signal bandwidth changing with the propagation length in triple-wavelength phase-matching QPCPA when the gain factor G=450 m-1 [(a),blue]and G=320 m-1 [(b),orange]. The parametric bandwidth and the simulated signal bandwidth changing with the propagation length in(c)noncollinear phase-matching QPCPA(yellow)and in(d)noncollinear phase-matching OPCPA(purple). The initial signal is centered at 810 nm with an F-T limit of 10 fs. The pump is centered at 532 nm,Ip/Is ≈3200,the crystal length z=50 mm and the absorption in QPCPA is 900 m-1. The solid lines are the upper limits of the parametric bandwidths,while the dashed lines are the lower limits,the dotted lines are the simulated signal bandwidth,and the dash-dotted lines are the simulated whole spectrum range of the signal.

The estimated parametric bandwidth and the simulated signal bandwidth in OPCPA and QPCPA are shown in Fig.5.In triple-wavelength phase-matching QPCPA,the signal bandwidth decreases whenz ＜z0G0/G′because of the gain distribution. The signal bandwidth rapidly increases to the parametric bandwidth maximum as shown in Fig.5(a)with a gain factorG0=450 m-1. Then the bandwidth increase is slowed down because the parametric bandwidth maximum requires a larger GV due to a longer propagation length. When the gain factor decreases to 320 m-1but the noncollinear angle remains 2.68°, the phase mismatch maximum located atω1is larger than the requirement of the parametric bandwidth so that the simulated signal bandwidth cannot reach the parametric bandwidth maximum,as shown in Fig.5(b). However,because the components at the phase-matching pointωpmcan be well amplified, the whole spectrum range can be larger than the parametric bandwidth maximum and reach the spectrum range which is supported by the noncollinear angle of 2.68°,as shown in Fig.5(a).When the QPCPA is operated ata=2.81°,the simulated signal bandwidth is close to the parametric bandwidth maximum as shown in Fig.5(c). In contrast,the signal bandwidth of noncollinear OPCPA can only reach the parametric bandwidth maximum in a small range aroundz=z0as shown in Fig.5(d).

When the QPCPA works at a noncollinear anglea=2.81°as the experiment in Ref.[10],and assume a seed pulse duration of 10 fs and a pump intensity of about 5 GW/cm2, the amplified spectrum in QPCPA can cover 750–930 nm, which is slightly broader than in OPCPA,as shown in Fig.6(a). The OPCPA spectrum is coincident with the experiment and the theoretical results using YCOB crystals in Refs. [20,21] as shown in Fig. 6(b). The bandwidth in QPCPA is continually increasing with the propagation length because the components with larger phase mismatch can be amplified to their theoretical conversion efficiency limit. However, the bandwidth extension is small because the phase mismatch is increasing rapidly. In OPCPA,the signal intensity and the spectrum bandwidth cannot be kept to their maximum with an improper crystal length. In QPCPA,the signal intensity and the bandwidth always are kept at their maximum when the crystal is long enough. When the noncollinear angle is set toa=2.68°, the spectrum in QPCPA can be extended to 700–950 nm,as shown in Fig.6(c). The amplified spectrum has a Fourier transform limit of～8 fs,even shorter than the seed. It is found that more short-wavelength components can be amplified ata=2.68°compared toa=2.81°. Therefore, this geometry is suitable for amplifying seeds that come from Tisapphire lasers or the white-light super-continuum generated by self-phase modulation. The former (Ref. [6]) has a spectrum covering 700–900 nm,and the latter(Ref.[22])has more short-wavelength components than the long-wavelength components.When the OPCPA works ata=2.68°,different spectral components cannot be amplified to their maximum with the same crystal length as shown in Fig.6(d). The bandwidth of OPCPA cannot be extended to the same as QPCPA under the triple-wavelength phase-matching geometry with a moderate gain factor.

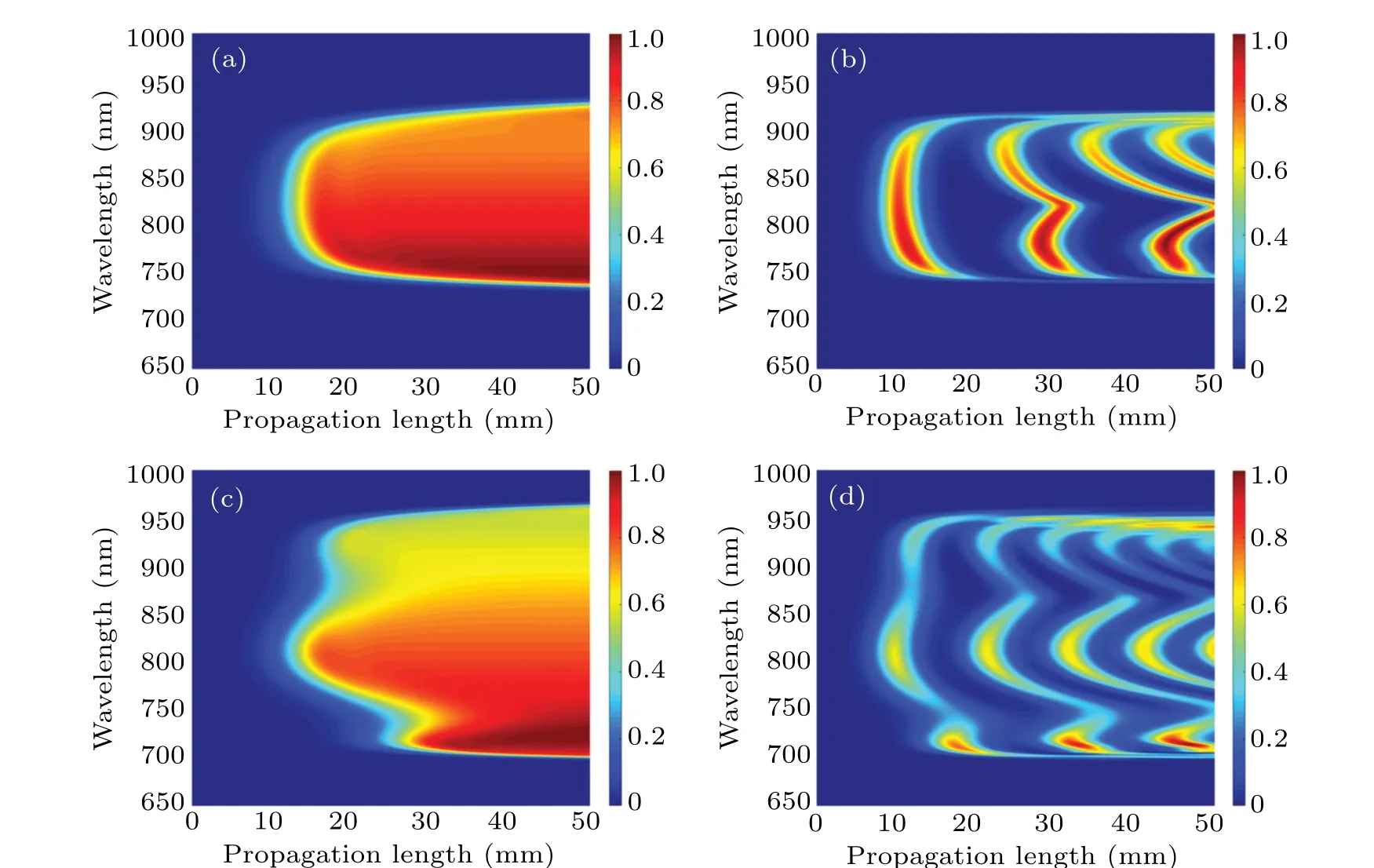
Fig.6. The spectrum with propagation length in(a)QPCPA with a=2.81°,(b)OPCPA with a=2.81°,(c)QPCPA with a=2.68°,and(d)OPCPA with a=2.68°,respectively. The spectrum is calculated with the central wavelength of 810 nm,and the pump intensity of 5 GW/cm2.The seed is centered at 810 nm with an F-T limit of 10 fs. The pump is centered at 532 nm with a fourth order super-Gaussian profile and Ip/Is ≈3200. The idler absorption in QPCPA is fixed at 900 m-1.

The conversion efficiency and the parametric bandwidth changes with the propagation length in QPCPA and OPCPA are shown in Fig. 7. The triple-wavelength scheme has the highest efficiency because the small components away from the central wavelength can be well amplified. It is impossible to get a large bandwidth by reducing the crystal length in OPCPA when the gain factor is limited to 450 m-1andIp/Is≈3200 in our simulation because the conversion efficiency is negligible. It is important that the bandwidth of QPCPA is increasing together with the conversion efficiency,which means that the signal bandwidth and the signal intensity can both reach their upper limits.

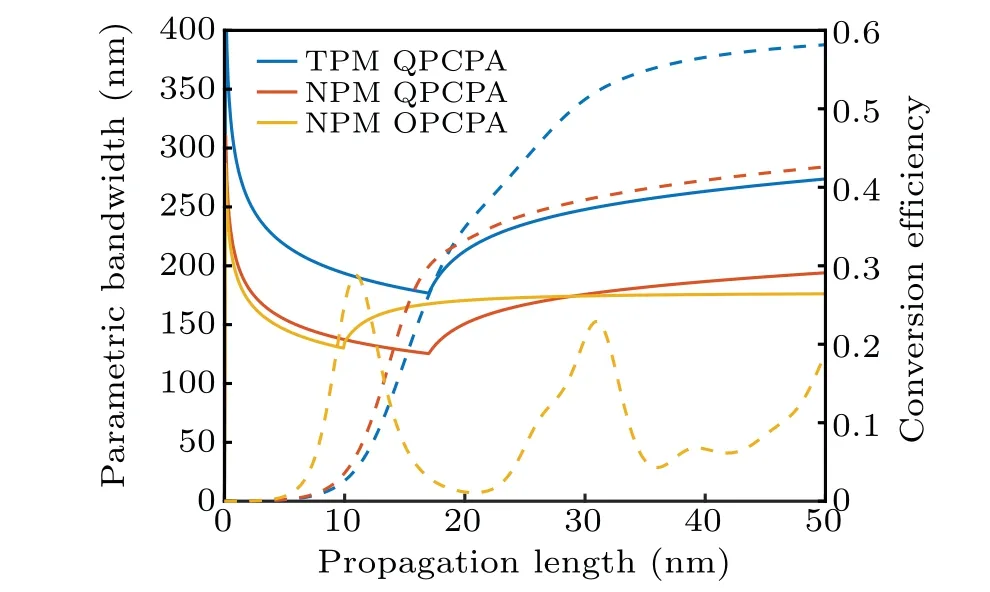
Fig. 7. The parametric bandwidth (solid lines) and the conversion efficiency (dashed lines) changing with the propagation length of the triple-wavelength phase-matching QPCPA (blue), the noncollinear phase-matching QPCPA(orange)and the noncollinear phase-matching OPCPA (yellow). The pulse duration of the pump is 150 ps with a fourth-order super-Gaussian profile, and the signal is stretched from 10 fs to 50 ps. The initial gain factor G0 ≈450 m-1, Ip/Is ≈3200 and the absorption is fixed at 900 m-1.

If the pump intensity changes in an established system,the spectrum and conversion efficiency may be changed dramatically. When the pump intensity changes from 5 GW/cm2to 2.5 GW/cm2, because of the unsuitable crystal length, the signal bandwidth in OPCPA is narrowed by 40 nm(as shown in Fig.8(a))and the conversion efficiency decreases to 42.5%compared to its maximum. In QPCPA, the narrowness of the signal bandwidth is much smaller than that in OPCPA,as shown in Figs. 8(b) and 8(c). When the noncollinear anglea=2.81°, the conversion efficiency is about 87% compared to the theoretical conversion efficiency limit. Whena=2.68°,the conversion efficiency remains about 80%,while the spectrum narrowing is negligible.

It is essential to analyze the nonlinear spectral phase in triple-wavelength phase-matching QPCPA. The origin of the spectral phase accumulation induced by the idler absorption is the different phase accumulation during the pulse transmission between the idler and the signal. When there is a phase mismatch in the amplifying process,an additional phase term∫exp(-jΔkz)dzappears in both newly generated idler and signal components.In OPCPA,this additional phase is equally added to the newly generated signal and idler,which produces a spectral phase-Δkz/2.

The phase of the amplified signal in OPCPA can be expressed as[23]

When the absorption is large enough,the phase accumulation is close to the material dispersion from the beginning to the end. When there is a strong idler absorption, the formerly generated idler is quickly absorbed,the newly generated idler has a phase close toΦp-Φs-Δkz. When the newly generated idler converts to signal,the phase of the newly generated signal is nearly the same as that of the existing signal. The signal is only experiencing the material dispersion. If highorder dispersion in the crystals can be ignored,the production of the uncompensable phase from the amplification process is strongly suppressed. Therefore, the corresponding spectral phase can be compensated for, and only the high-order dispersion due to the non-uniformity of the absorption spectrum remains. The dispersion induced by absorption spectrum nonuniformity can be large if a strong absorption peak is placed at a large phase mismatch region and a weak absorption valley is placed at the small phase mismatch region. A uniform absorption spectrum is impossible to be achieved. Therefore strong absorption peaks should be ensured in the small phase mismatch region to decrease the phase difference between those components.

When a uniform absorption spectrum is used, the spectral phase of signals after amplified by a 50-mm-long crystal can be well controlled by a high order dispersion control up to 6thorder, as shown in Fig. 8(c). However, if there is no idler absorption, the spectral phase cannot be well controlled even with high order dispersion control, as shown in Fig.8(d). In a triple-wavelength phase-matching QPCPA,the required absorption spectrum is possibly formed by multiple absorption peaks. Assuming an absorption spectrum as shown in Fig.8(e),the residual spectral phase is highly modulated by the nonuniformity of the absorption spectrum. In the large dispersion region,the nonlinear spectral phase in QPCPA with such an absorption spectrum is smaller than the nonlinear spectral phase in OPCPA.On the other hand, the remaining spectral phase using a non-uniform absorption spectrum is larger than the nonlinear spectral phase using a uniform absorption spectrum, as shown in Fig. 8(d). Therefore, it leads to minor side pulses,as shown in Fig.8(f).

Fig. 8. The spectrum and spectral phase after dispersion control up to 6th order of (a) noncollinear OPCPA, (b) noncollinear QPCPA, (c)triple-wavelength phase-matching QPCPA, (d) triple-wavelength phase-matching QPCPA with multi-peaks absorption, respectively. (e) The absorption spectrum in(d). (f)The pulse duration after dispersion control. The seed is centered at 810 nm with an F-T limit of 10 fs. The pump is centered at 532 nm and Ip/Is ≈3200. The absorption in(b)and(c)is fixed at 900 m-1.

The pulse duration after dispersion management is shown in Fig. 8(f). The pulse duration is 12.5 fs when amplified with the noncollinear OPCPA scheme at the pump intensity of 5 GW/cm2. When the pump intensity is changed to 2.5 GW/cm2, the pulse duration in OPCPA is expended to 14.5 fs. The pulse duration after amplifying by triplewavelength phase-matching QPCPA can achieve 7.92 fs,which is close to its Fourier transform limits. The shortest pulse duration, 7.92 fs, is obtained by a dispersion control up to 6thorder, which can be achieved by applying an acousto-optic programmable dispersive filter (AOPDF). The high-order dispersions in triple-wavelength phase-matching QPCPA are large because of the relatively larger phasemismatch and the absorption distributions in the broadband spectrum. The dispersions are group delay dispersions(GDD)=4418 fs2,third-order dispersions(TOD)=3767 fs3,fourth-order dispersions (FOD) = 5147 fs4, fifth-order dispersions (FiOD) = 104040 fs5and sixth-order dispersions(SOD)=615672 fs6when using a uniform absorption spectrum,respectively. Therefore,dispersion control up to the 3rdorder is required. Meanwhile, the dispersions are GDD =4430 fs2, TOD = 2662 fs3, FOD =-1168 fs4, FiOD =322680 fs5and SOD=578952 fs6when using a multi-peaks absorption spectrum,respectively. As a result,dispersion control up to the 5thorder is necessary. If the dispersions are controlled up to 3rdorder or 4thorder with a uniform absorption spectrum, the uncompensated phase within the spectrum is±0.6π,showing a pulse duration～7.92 fs with small side peaks (about 10% of the maximum intensity). The uncompensated phase within the spectrum is±0.2πwith a dispersion control up to 5thor 6thorder with no side peaks. If the dispersions are controlled up to 3rdorder or 4thorder with a multi-peaks absorption spectrum,the uncompensated phase within the spectrum is±1.8πwhile showing large side peaks(about 60% of the maximum intensity). The uncompensated phase within the spectrum is±0.6πwith a dispersion control up to 5thor 6thorder, side peaks almost disappear. The pump intensity changes almost do not change the pulse duration, which means triple-wavelength phase-matching QPCPA is very insensitive towards pump intensity fluctuations. These results show that QPCPA is tailored to broadband amplification at a limited pump intensity, which has great potential in full-OPCPA petawatt laser systems.

5. Conclusion

In conclusion,we have described the evolution of the signal in the quasi-parametric amplification process and proved that QPCPA is suitable for broadband amplification. We have modeled and developed a novel noncollinear phase-matching geometry in QPCPA, named as the triple-wavelength phasematching geometry, and compared this scheme with the noncollinear geometry commonly used in OPCPA.Adjusting the noncollinear angle to the triple-wavelength phase-matching point allows the signal bandwidth to about 260 nm when the pump intensity is limited to 5 GW/cm2in a doped YCOB crystal. This scheme provides a much broader bandwidth in QPCPA than the 150 nm bandwidth in noncollinear OPCPA.The results show that the pulse duration of the signal amplified by the triple-wavelength phase-matching QPCPA can achieve 7.92 fs, which is even shorter than the Fourier transform limit of the seed pulses. Furthermore,the pulse duration and the conversion efficiency are stable when the pump intensity changes from 5 GW/cm2to 2.5 GW/cm2, showing its great potential in few-cycle full-OPCPA petawatt lasers. The quasi-parametric amplifying process can overcome the high order dispersion induced by the phase mismatch. However,the nonuniformity of the absorption spectrum leads to another set of high order dispersion,which does not expend the pulse duration but brings several minor side peaks in the time domain.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(Grant No.51832009)and the Fundamental Research Funds for the Central Universities, China(Grant No.2019YJS209).