A Study of ρ-ω Mixing in Resonance Chiral Theory∗
Yun-Hua Chen(陈云华) De-Liang Yao(姚德良) and Han-Qing Zheng(郑汉青)§
1School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China
2Instituto de F´ısica Corpuscular(Centro Mixto CSIC-UV),Institutos de Investigaci´on de Paterna,Apartado 22085,46071,Valencia,Spain
3Department of Physics and State Key Laboratory of Nuclear Physics and Technology,Peking University,Beijing 100871,China
4Collaborative Innovation Center of Quantum Matter,Beijing 100871,China
1 Introduction
The study ofρ-ωmixing is a very interesting subject in hadron physics both theoretically and experimentally.The inclusion ofρ-ωmixing effect is crucial for a good description of the pion vector form factor ine+e−→π+π−process,which quanti fies the hadronic vacuum polarization contribution to the anomalous magnetic moment of the muon.On the experimental side,several experimental collaborations,such as KLOE[1−2]and BESIII,[3]have recently launched measurements of thee+e−→π+π−with high statistics and high precision.
Theρ-ωmixing amplitude was assumed to be a constant or momentum-independent in the early stage of previous studies.[4−5]The authors of Ref.[6]suspected the validity of the constant assumption and,based on a quark loop mechanism ofρ-ωmixing,they found that the mixing amplitude is signi ficantly momentum-dependent.Since then,the use of various loop mechanisms forρ-ωmixing is triggered in different models such as extended Nambu-Jona-Lasinio(NJL)model,[7]the global color model,[8]the hidden local symmetry model,[9−11]and the chiral constituent quark model.[12−13]
In this work,we aim at studyingρ-ωmixing in a model independent way by invoking Resonance Chiral Theory(RχT).[14]It provides a reliable tool to study physics in the intermediate energy region.[15−20]The tree-level calculation ofρ-ωmixing in the framework of RχT has been given in Refs.[21–22],however,the tree-level mixing amplitude turns out to be momentum-independent.In order to implement the momentum dependence,here we will calculate the one-loop contributions as shown in Fig.1.Theρ-ωmixing can be induced either by strong isospinviolating or by electromagnetic effects.The former is proportional to the mass difference bewteen theu,dquarks,i.e.,∆ud=mu−mdand the latter is accompanied by the fine structure constantα.In the present study,only the mixing effects linear in ∆udorαare under our consideration.Apart from the overall factors ∆udorα,the large-NCcounting rule proposed in Ref.[23]is imposed to truncate our perturbative calculation.Speci fically,our calculations are truncated at next-to-leading order in the 1/NCexpansion for the strong and electromagnetic contributions.The ultraviolet(UV)divergence from the loops is cancelled by introducing counterterms with sufficient derivatives and the involved couplings are assumed to be beyond the leading order in 1/NCexpansion as claimed in Ref.[24].
We assess the impact of momentum-dependentρ-ωmixing amplitude on the pion vector form factor by fitting to the experimental data extracted from thee+e−→π+π−process andτ→ντ2πdecay in the energy region of(650–850)MeV.Besides,the decay width ofω→π+π−is implemented as a constraint in the fit.It is known that,provided isospin invariance holds,the isovector part of the pion form factor in thee+e−annihilation is related to the one inτdecays theoretically,via the conserved vector current assumption.[25−26]Different effects of isospin breaking have been studied to describe thee+e−annihilation data andτdecays data simultaneously,[26−34]such as the short distance and long distance corrections in theτpartial decay width to two pions,charged and neutralρmass and width difference,andρ-ωmixing.In our study we will take into account all the above isospin breaking effects.Our fit result shows that theρ-ωmixing amplitude is signi ficantly momentum-dependent and its imaginary part is much smaller than real part.Based on the fitted values of the parameters,we also analyze the decay width ofω→π+π−by including the effect of theρ-ωmixing.It is found that the decay width is dominated by theρ-ωmixing effect while the contribution from the direct coupling ofωI→π+π−is negligible.
This paper is organized as follows.In Sec.2,we introduce the description ofρ-ωmixing.In Sec.3,we present the theoretical framework and elaborate on the calculation of the tree-level and loop contribution ofρ-ωmixing.In Sec.4,the fit result is shown and the related phenomenology is dicussed.A summary is given in Sec.5.
2 Generic Description of ρ-ω Mixing
In the isospin basis|I,I3>,we de fine|ρI>≡|1,0>and|ωI>≡|0,0>for convenience.The mixing between the isospin states of|ρI>and|ωI>can be implemented by considering the self-energy matrix

In above the vector-current conservation has been used to eliminate the longitudinal part proportional topµ.Furthermore,we have also neglected terms ofsince they correspond to contributions at two-loop order and are beyond our accuracy.mρandmωare bare masses of theρandωmesons,respectively.
Theρ-ωmixing,i.e.,mixing between the physical states ofρ0andω,is obtainable by introducing the following relation

withϵbeing the mixing parameter.The matrix of dressed propagators corresponding to physical states is diagonal.Moreover,it can be connected to the matrixDI(s)in Eq.(2)through

The two mixing parameters should be just different with each other slightly,see Ref.[35]for more details.
3 Calculations in Resonance Chiral Theory
In this section we will calculate the mixing amplitude Πρω(s)using RχT so as to study its momentum dependence.The information ofρ-ωmixing is encoded in the o ff-diagonal element of the self-energy matrix,which can be decomposed as

where∆ud=mu−mdis the mass difference betweenu,dquarks,andαdenotes the fine-structure constant.In above,Sρω(s)andEρω(s)stand for the structure functions of strong and electromagnetic interactions,respectively.In the present work,the diagrams in Fig.1 are needed for a calculation in RχT up to NLO in 1/NCexpansion.As will be seen below,the LO contributions ofSρω(s)andEρω(s)are different:the former starts atwhile the latter does atTherefore,their corresponding NLO contributions are ofand,respectively.In what follows,all the diagrams in Fig.1 will be calculated by using effective Lagrangians constructed in the framework of RχT.
3.1 Resonance Chiral Theory and Tree-Level Amplitudes
In RχT,the vector resonances are described in terms of antisymmetry tensor fields with the normalization

withϵµbeing the polarization vector.The kinetic Lagrangian of vector resonances takes the form[14]

¶Without loss of generality,here we use the Proca formalism for the vector fields andTµνis the transverse projector.In the antisymmetric tensor formalism,the corresponding transverse projector is
whereMVis the mass of the vector resonances in the chiral limit.Here the vector mesons are collected in a 2×2 matrix

Hereare field strength tensors composed of the left and right external sourceslµandrµ,andFV,GVare real couplings.
The LO isospin-breaking effect is introduced by the Lagrangian


Fig.1 Feynman diagrams contributing to ρ-ω mixing.
3.2 Loop Contributions
The relevant loop diagrams contributing up to our accuracy are shown in the second and third lines of Fig.1.Diagrams(c)and(d)contribute to the strong correction at,which are next-to-leading order compared to diagram(a).Likewise,with respect to diagram(b),diagrams(e)–(h)lead to electromagnetic corrections at nextto-leading order,i.e..In our calculation below,the necessary isospin-breaking vertices are constructed based on the basic chiral building blocks taken fromχPT[36]and RχT.[14]
(i)Diagram(c):ππ Loop
The vertex ofρI→π+π−can be read from the Lagrangian in Eq.(13).For the isospin-violating vertex ofωI→π+π−,we construct the following Lagrangian

For convenience,we de fine the combinationTheππ-loop contribution can be obtained by calculating the integral
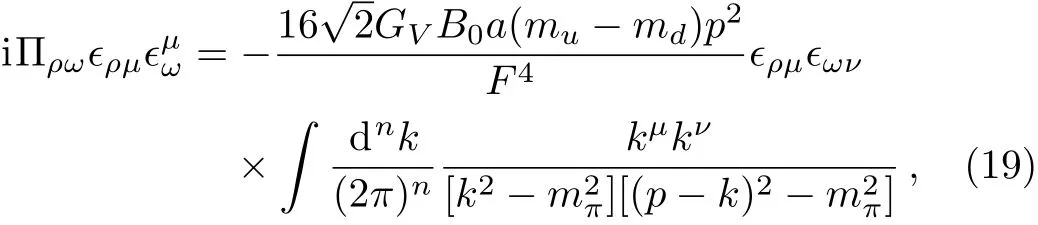
wherepandkdenote the momenta of the external vector meson and either of the exchanged pions,respectively.After integrating,the structure function can be extracted,which reads

(ii)Diagram(d):π-Tadpole Loop
According to the Lorentz,PandCinvariances,the Lagrangian corresponding to the interaction ofωIρIππcan be written down as follows:

Note that thev8⟨VµνVµνχ+>term,which contributes to the contact interaction ofρ-ωmixing,also yieldsωIρIππvertex.Though in Eq.(21)there are many terms with a large number of free couplings,the final result only depends on combinations of these couplings.For simplicity,the following two combinations are necessary,i.e.,
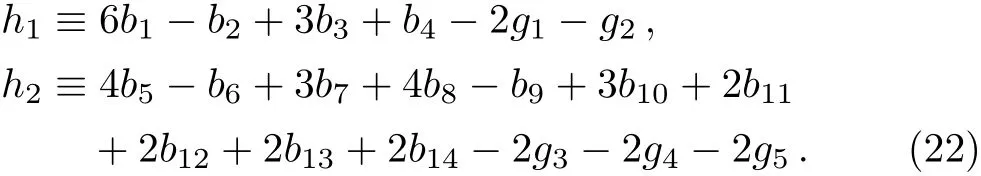
Furthermore,one can neglect the mass difference between the charged and neutral pions in the internal lines of loops,since the resultant difference is of higher orders beyond our consideration.As a result,the expanded form of Lagrangian(21)can be reduced simply to

With the above Lagrangian,theπ-tadpole contribution to theρ-ωmixing can be derived:

Eventually,the explicit expression of the strong structure function has the form of

(iii)Diagrams(e)–(h):π0γLoops
In the loop diagrams(e)–(h),there are two types of vertices.The coupling of vector meson(V)as well as vector external source(J)to pseudoscalar(P)is labeled by VJP vertex for short.The interaction of two vector mesons and one pseudoscalar is called VVP vertex.The operators of VJP type are given in Ref.[37]:


The involved couplings or their combinations can be estimated by matching the leading operator product expansion of⟨VVP>Green function to the result calculted within RχT.Such a procedure leads to high energy constraints on the resonance couplings as follows:[37]

The mass of vectors in the chiral limit,MV,can be estimated by the mass ofρ(770)meson.[38]
The loops diagrams(e)–(h)can be calculated simultanously if the effective vertices ofandω∗are used,where a “∗” stands for an o ff-shell particle.The explicit expression forreads

It should be stressed that there are two terms in each effective vertex.One corresponds to the case that the virtual photon is coupled to the VP system directly,while the other to the case that it is interacted through an intermediate vector meson.Note also that,throughout this work we only account for the corrections proportional either to∆udor 4πα,which implies the calculation of electromagnetic contribution can be carried out in the isospin limit,i.e.,mu=md.
With the help of the effective vertices,theπγloop contribution,i.e.,the sum of the loops diagrams(e)–(h),can be expressed as:
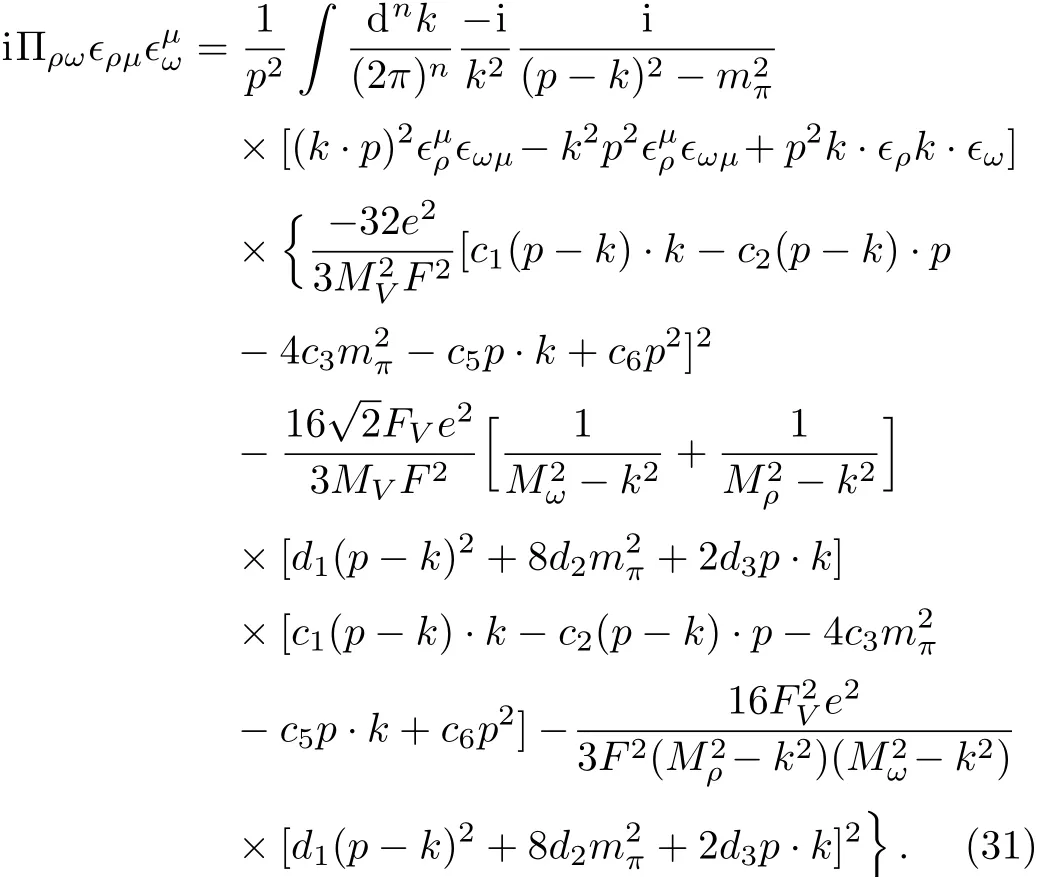
The further calculation is straightforward but the result of the extracted electromagnetic structure functionis too lengthy to be shown here.It is worthy noting that in our numerical computation we will use the high energy constraints in Eq.(28)together with the fitted parameters given in Ref.[18],therefore,all the parameters involved inare known.
(iv)Counterterms and Renormalized Amplitude
Up to now,the total contribution ofρ-ωmixing can be expressed as

which is still unrenormalized.The resonance chiral theory is unrenormalizable in the sense that the amplitude has to be renormalized order by order with increasing number of counterterms when the accuracy of the calculation is improved.In our case,the tree amplitudes,can only absorb the ultraviolet divergence proportional top0.In order to cancel thestemming from the loop contributionSadditional counterterms are needed.For this purpose,we construct


where a bar indicates the divergences are subtracted.As discussed in Ref.[35],there is an important constraint on the mixing amplitude,namely,it should vanish asp2→0.Thus the final expression of the renormalized mixing amplitude should be

where an additional finite shift is imposed so as to guarantee that the constraint Πρω(0)=0 is satis fied.
In our numerical computation,the scaleµwill be set toMρand we use(mu−md)=−2.49 MeV provided by particle data group(PDG).[39]Furthermore,we can de fine

and in principle the unknown parameters in Eq.(35)area,
4 The Effect of ρ-ω Mixing on Pion Vector Form Factor
The mass and width ofρmeson are conventionally determined by fitting to the data ofe+e−→π+π−andwhere various mechanisms are introduced to describe theρ-ωmixing effect.To avoid intervening by theirρ-ωmixing mechanisms,we do not employ their extracted values for the mass and width,rather,we set the massMρ,the relevant couplingsGρandFρto be free parameters in our fit.As for the width,an energy-dependent form will be imposed,which is supposed to be dominated by the twoπdecay channel:[40]

and get138 MeV.With the decay widths given above,sρandsωin Eq.(3)now can be rewritten as
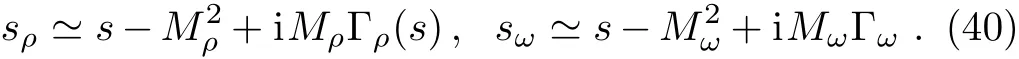
The experimental data considered in this work are the pion form factorof theprocess[1−3,41−45]anddecay[25,46]in the energy region of(650–850)MeV,and the decay width of
The Feynman amplitude for the processproceeding via virtual intermediate hadrons,i.e.,ρ,ωand their mixing,is described by[35]

Here the fourth term corresponds to higher-order contribution of isospin breaking,e.g.,proportional to(mu−md)2,which is beyond our accuracy and hence can be neglected.Including the contribution from the direct coupling of photon to the pion pair,the pion form-factor ine+e−annihilation reads

which is irrelevant toρ-ωmixing effect.To take into account the isospin breaking effects,one way is to multi-by the factor of,whereSEW=1.0233 corresponding to the short distance correction.[26]Furthermore,GEM(s)is responsible for the long distance radiative correction whose expression is provided in Ref.[47].To be speci fic,in our fit we make the following substitution

Our best- fitted parameters and the correspondingχ2/d.o.f.are compiled in Table 1.Our determination of the mass ofρmeson is in good agreement with the value reported in PDG.[39]The fit results are plotted in the Fig.2.One can see that the experimental data of pion form factor,especially the kink around the mass ofωin theprocess,is well described.
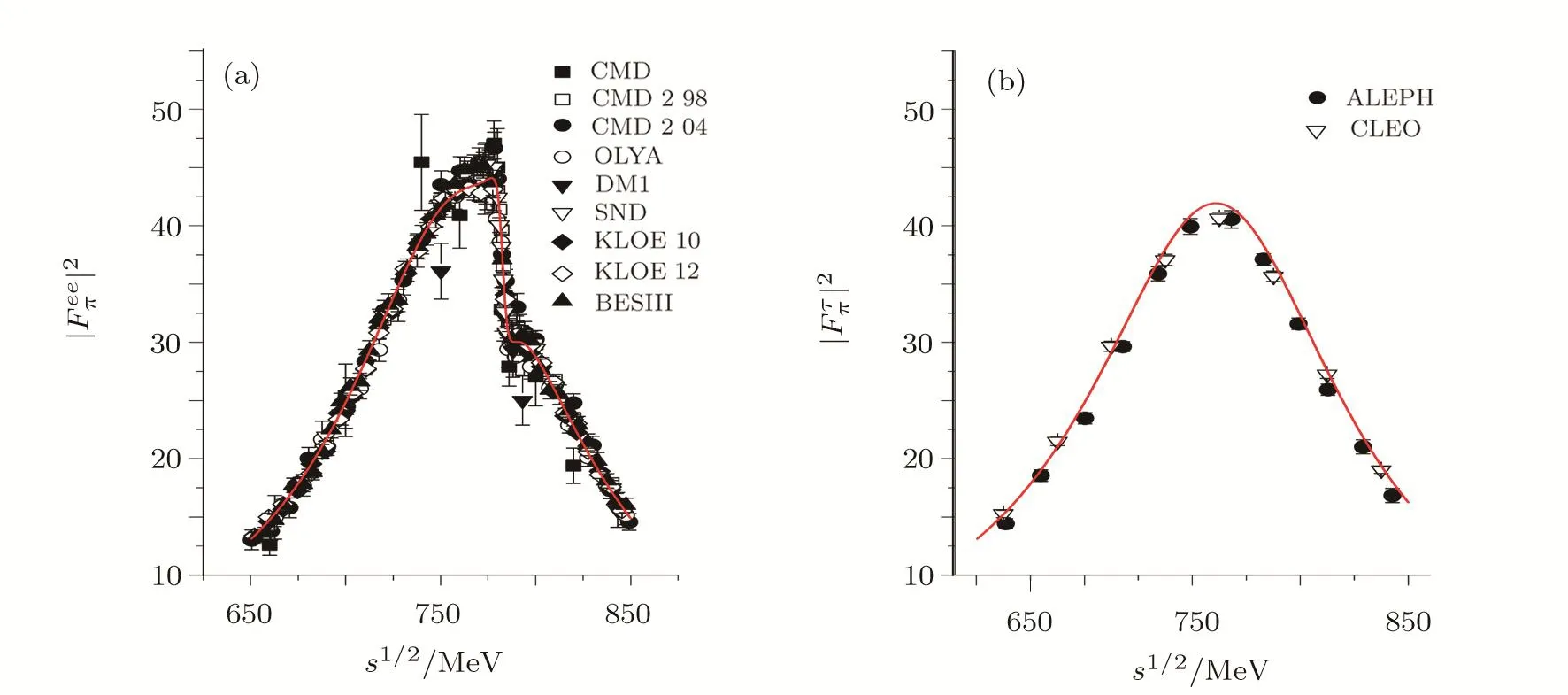
Fig.2 (Color online)Fit results for the pion form factor in the e+e− → π+π− process(a)and τ→ ντ2π process(b).The data of e+e− annihilation are taken from the OLYA and CMD,[41]CMD2,[42−43]DM1,[44]SND,[45]KLOE,[1−2]BESIII[3]collaborations.The τ decay data are taken from the ALEPH[46]and CLEO[25]collaborations.The solid lines are our theoretical predictions.
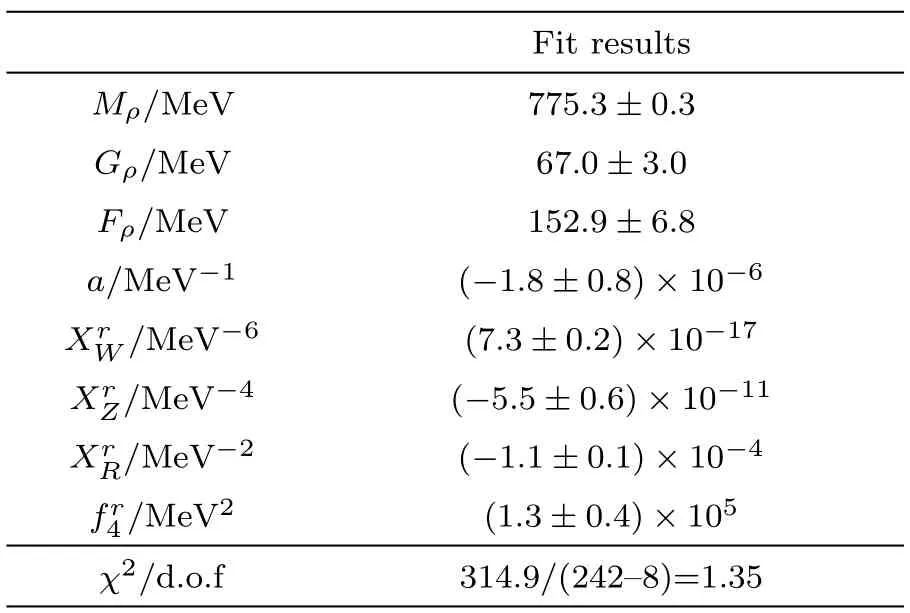
Table 1 The fit results of the parameters.
In Fig.3,contributions at different orders to the real and imaginary parts of the pion form factorare displayed.The leading-order contribution(mixing-effect irrelevant)includes the contact interaction and theρmediated mechanism,namely the first two terms on the right side of Eq.(41).The next-to-leading-order contribution includes theρ-ωmixing term and the directωIππcoupling,namely the third term plus the forth term on the right side of Eq.(41).As expected,the isospin-breaking effects mainly affects the energy region around the masses ofρandω.It is found that the dominant contribution is from the imaginary part in that region.The isospinbreaking effects increase the absolute value of imaginary part around theρpeak,and accounts for that thee+e−data are higher than theτdata in that region as shown in Fig.2.Similar behavior has also been observed in Ref.[11]where theρ-ωmixing was treated in hidden local symmetry model.
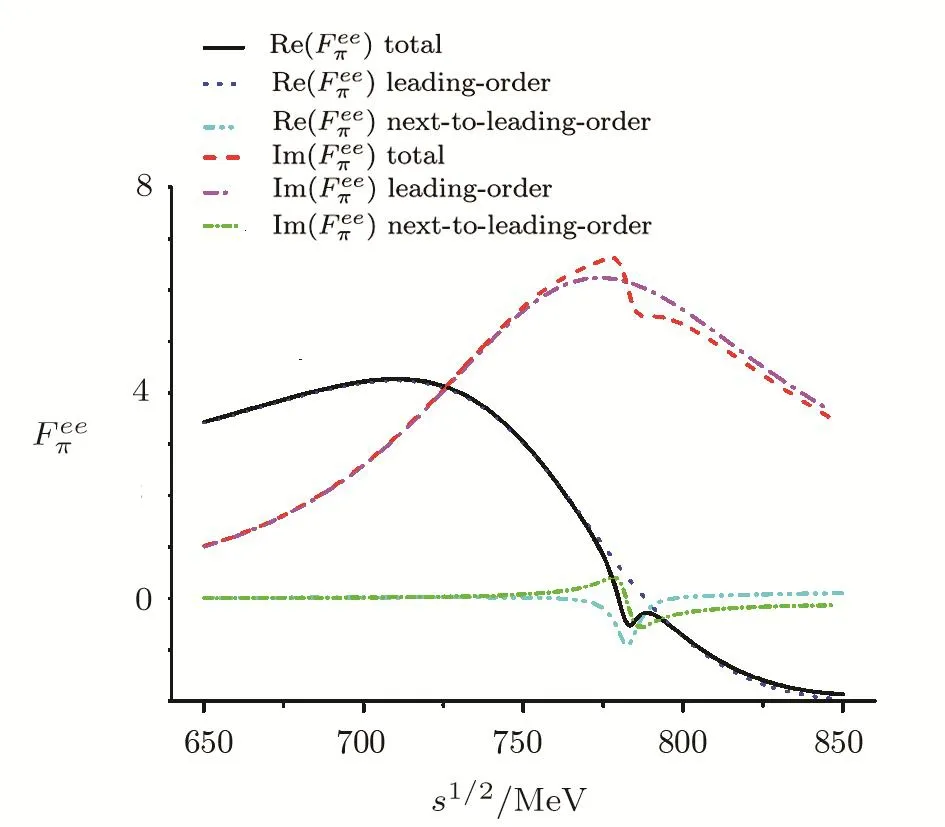
Fig.3 (Color online)The real and imaginary parts of the fitted form factor Feeπ(s).The black solid and red dashed lines represent our best results of the real and imaginary parts,respectively.The blue dotted and cyan dash-dot-dotted lines correspond to the leading order and the second order contributions of the real parts,respectively.The magenta dash-dotted and green short dashdash-dotted lines denote the leading order and second order contributions of the imaginary parts.
In Fig.4,we plot the real and imaginary parts of the mixing amplitude Πρω(s).It is found that the real part is dominant almost in all the region and its momentumdependence is signi ficant.Compared to the real part,the imaginary part is rather small.For the imaginary part,the contributions fromππloop andπγloop are of the same order,but with opposite sign.Note that theπ-tadpole is real ands-independent as can be seen from Eq.(25).The smallness of the imaginary part is consistent with the observation in Refs.[5,48],though therein the effect of directωI→π+π−was not taken into account and even in Ref.[5]the isospin breaking is considered to be purely electromagnetic origin.We also note that larger imaginary part is obtained in Refs.[8,13]by using global color model and a chiral constituent quark model,respectively.
However,our finding is more reliable in the sense that it is based on a model-independent description of theρ-ωmixing and,moreover,constraint from experimental data is imposed by means of fitting.
The values of Πρωat physical masses ofρorωare interesting since they are related to the mixing parameters given in Eq.(6).To that end,we obtain:MeV2,andϵ2=0.21;MeV2andϵ1=0.24.As expected,ϵ1andϵ2come out to be almost the same.Note that,in the numerical calculation ofϵi,we have neglected the small imaginary part of the mixing amplitude as well as the widths of theρandωresonances.This leads to a real number ofϵiand hence a probability interpretation can be assigned.

Fig.4(Color online)The real part(a)and imaginary part(b)of the mixing amplitude Πphysicalρω(s).The black solid lines represent our best fitted results.For the imaginary part,the red dashed and blue dotted lines correspond to the contribution of ππ loop and πγ loop,respectively.
Using the central values of the fitted parameters in Table 1,we calculate the decay width of
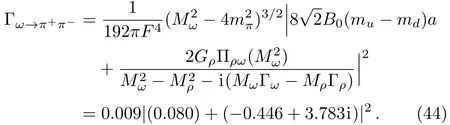
From Eq.(44),we can find that the first term due to the directis less than the second term due to theρ-ωmixing by two orders.In other words,the directcoupling only affects the decay width less than one percent.Within 1σuncertainties,our theoretical value of the branching fraction is(1.53±0.10)×10−2,which agrees with the values given in PDG[39]and by the recent dispersive analysis.[49]
5 Summary
We have analyzed theρ-ωmixing within the framework of resonance chiral theory.Based on the effective Lagrangians constructed under the guidance of various symmetries,we calculate theρ-ωmixing amplitude up to next-to-leading order in large 1/NCexpansion.Importantly,the momentum-dependent effect is implemented due to the inclusion of loops in our calculation.The values of the resonance couplings are determined by fitting to the data of the pion vector form factor extracted from theprocess anddecay.The decay width ofis served an additional constraint in the fit as well.It is found that the imaginary part of the pion form factoris enhanced largely around theρpeak.Theρ-ωmixing amplitude is dominated by its real part almost in all the region,which is signi ficantly momentum-dependent.On the contrary,its imaginary part is relatively small.We also find thatρ-ωmixing plays a major role in the decay width of,and its contribution is two orders of magnitude larger than that from the directωIππcoupling.
We would like to thank A.Hosaka and J.J.Sanz-Cillero for helpful discussions.
[1]KLOE Collaboration,F.Ambrosino,et al.,Phys.Lett.B700(2011)102.
[2]KLOE Collaboration,D.Babusci,et al.,Phys.Lett.B720(2013)336.
[3]BESIII Collaboration,M.Ablikim,et al.,Phys.Lett.B753(2016)629.
[4]S.L.Glashow,Phys.Rev.Lett.7(1961)469.
[5]F.M.Renard,Springer Tracts in Modern Physics,6398-120,Springer-Verlag,Berlin(1972).
[6]T.Goldman,J.A.Henderson,and A.W.Thomas,Few Body Systems12(1992)123.
[7]C.M.Shakin and W.D.Sun,Phys.Rev.D55(1997)2874.
[8]K.L.Mitchell and P.C.Tandy,Phys.Rev.C55(1997)1477.
[9]M.Benayoun,et al.,Eur.Phys.J.C17(2000)303.
[10]M.Benayoun,et al.,Eur.Phys.J.C22(2001)503.
[11]M.Benayoun,et al.,Eur.Phys.J.C55(2008)199.
[12]D.N.Gao and M.L.Yan,Eur.Phys.J.A3(1998)293.
[13]X.J.Wang and M.L.Yan,Phys.Rev.D62(2000)094013.
[14]G.Ecker,J.Gasser,A.Pich,and E.de Rafael,Nucl.Phys.B321(1989)311.
[15]Z.H.Guo and J.A.Oller,Phys.Rev.D84(2011)034005.
[16]M.Jamin,A.Pich,and J.Portoles,Phys.Lett.B640(2006)176.
[17]P.Roig and J.J.Sanz-Cillero,Phys.Lett.B733(2014)158.
[18]Y.H.Chen,Z.H.Guo,and H.Q.Zheng,Phys.Rev.D85(2012)054018.
[19]Y.H.Chen,Z.H.Guo,and H.Q.Zheng,Phys.Rev.D90(2014)034013.
[20]Y.H.Chen,Z.H.Guo,and B.S.Zou,Phys.Rev.D91(2015)014010.
[21]Res Urech,Phys.Lett.B355(1995)308.
[22]A.Kucukarslan and Ulf-G.Meißner,Mod.Rev.Lett.A21(2006)1423.
[23]G.t’Hooft,Nucl.Phys.B72(1974);ibid.75(1974)461.
[24]I.Rosell,J.J.Sanz-Cillero,and A.Pich,JHEP0408(2004)042.
[25]CLEO Collaboration,S.Anderson,et al.,Phys.Rev.D61(2000)112002.
[26]M.Davier,et al.,Eur.Phys.J.C27(2003)497.
[27]R.Alemany,et al.,Eur.Phys.J.C2(1998)123.
[28]J.A.Oller,E.Oset and J.E.Palomar,Phys.Rev.D63(2001)114009.
[29]V.Cirigliano,et al.,Phys.Lett.B513(2001)361.
[30]V.Cirigliano,et al.,Eur.Phys.J.C23(2002)121.
[31]S.Ghozzi and F.Jegerlehner,Phys.Lett.B583(2004)222.
[32]K.Maltman and C.E.Wolfe,Phys.Rev.D73(2006)013004.
[33]L.Y.Dai,J.Portoles,and O.Shekhovtsova,Phys.Rev.D88(2013)056001.
[34]D.Djukanovic,J.Gegelia,A.Keller,S.Scherer,and L.Tiator,Phys.Lett.B742(2015)55.
[35]H.B.O’Connell,B.C.Pearce,A.W.Thomas,and A.G.Williams,Prog.Nucl.Part.Phys.39(1997)201.
[36]J.Gasser and H.Leutwyler,Annals Phys.158(1984)142;J.Gasser and H.Leutwyler,Nucl.Phys.B250(1985)465.
[37]P.D.Ruiz-Femenia,A.Pich,and J.Portoles,JHEP0307(2003)003.
[38]V.Mateu and J.Portoles,Eur.Phys.J.C52(2007)325.
[39]C.Patrignani,et al.,[Particle Data Group Collaboration],Chin.Phys.C40(2016)100001.
[40]D.Gomez-Dumm,A.Pich,and J.Portoles,Phys.Rev.D62(2000)054014.
[41]L.M.Barkov,et al.,Nucl.Phys.B256(1985)365.
[42]CMD-2 Collaboration,R.R.Akhmetshin,et al.,Phys.Lett.B578(2004)285.
[43]CMD-2 Collaboration,R.R.Akhmetshin,et al.,JETP Lett.84(2006)413.
[44]A.Quenzer,et al.,Phys.Lett.B76(1978)512.
[45]M.N.‘Achasov,et al.,J.Exp.Theor.Phys.103(2006)380.
[46]ALEPH Collaboration,S.Schael,et al.,Phys.Rep.421(2005)191.
[47]F.Flores-Baez,et al.,Phys.Rev.D74(2006)071301.
[48]S.Gardner and H.B.O’Connell,Phys.Rev.D57(1998)2716.
[49]C.Hanhart,S.Holz,B.Kubis,et al.,Eur.Phys.J.C77(2017)98.
 Communications in Theoretical Physics2018年1期
Communications in Theoretical Physics2018年1期
- Communications in Theoretical Physics的其它文章
- Electron Acceleration by Beating of Two Intense Cross-Focused Hollow Gaussian Laser Beams in Plasma∗
- Spatial Dependent Spontaneous Emission of an Atom in a Semi-In finite Waveguide of Rectangular Cross Section∗
- Unique Outcomes of Internal Heat Generation and Thermal Deposition on Viscous Dissipative Transport of Viscoplastic Fluid over a Riga-Plate
- Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow∗
- Ti Impurity Effect on the Optical Coefficients in 2D Cu2Si:A DFT Study∗
- Solitary Potential in a Space Plasma Containing Dynamical Heavy Ions and Bi-Kappa Distributed Electrons of Two Distinct Temperatures
