不同边坡治理方式治理效果对比研究

郑仕跃，彭文彬，张仁坤，冯安治

(中海建筑有限公司，广东 深圳 518053)

1 引 言

在自然因素和人为因素的共同作用下，边坡的岩土抗剪强度随时间不断衰减，出现各种病害，严重影响公路建设、运营以及养护等各阶段的安全，同时增加了成本。

滑坡属于最常见的边坡病害，边坡表面的岩体受到外部因素干扰后，顺着边坡滑面(边坡软弱面)整体向下滑动的一种边坡病害。当边坡具有明显的天然软弱面，在水的影响下，极易发生滑坡。发生滑坡后的边坡岩土体依然具有完整的岩性结构。

目前，边坡病害处治技术发展逐渐趋于成熟，根据各地区地质、工程特点，防治措施的选择还没有形成统一的标准。目前较为常见的措施有坡率控制法(削坡法)、排水法和岩土锚固技术。

削坡减载指的是通过对边坡及时进行平整和刷帮，根据实际情况采取合适的削坡方案，改变边坡的轮廓和形状，从而提高边坡整体稳定性的边坡病害防治方法。学者和工程师们从削下坡体的运载方式[1]、不同的削坡角度[2]以及对水这一因素的不同考虑方式[3]切入，开展了广泛的研究。

水是边坡中极不稳定的因素之一。由于土这种材料的性质与含水量密切相关，在强降雨等条件下土质边坡极易发生失稳。关于土中水对边坡稳定性的影响，研究者们已有一定的研究基础[4-6]。

抗滑桩加固作为一种常见的边坡加固方法，具有因地制宜、施工方法多样以及加固效果好等特点。国内很早就开始了对于抗滑桩的多方面研究。从不同分析方法[7，8，17]，不同桩径[9，15，16]、不同桩体截面形状[10]、不同布设位置及形式[11-16]以及不同布设场地条件[9]等方面开展了广泛的研究。

通过ABAQUS建立了天然边坡、经削坡处理后的边坡以及布设抗滑桩的边坡模型，通过计算得到了各模型下的安全系数；通过对抗滑桩进行精细化建模，将桩土模型计算得到的桩顶位移施加在精细化模型上，研究了抗滑桩在滑坡发生过程中的响应特性，并找出了桩身应力集中的位置。

2 边坡有限元模拟

2.1 模型与本构

如图1所示，依托贵州省正习高速十七标内一公路边坡建立分析模型。边坡高12 m，坡率为0.75∶1。模型中，坡脚向外部、底部延伸5 m，坡顶向外延伸9 m。经计算，所取小边界与常规边界(坡脚向外部、底部延伸1.5倍坡高，坡顶向外部延伸2.5倍坡高)计算结果差异不超过5%，出于简化计算考虑，取小边界模型。

图1 边坡断面布置图

采用Mohr-Coulomb模型来描述土的变形特征，该模型即能够描述土体变形的基本特征，简单实用，参数少。出于简便考虑，对土体进行了均一化处理。土体密度为1.78 g/cm3，杨氏模量为60 MPa，泊松比为0.3，内摩擦角取为18°，粘聚力取为16 kPa。边坡模型中抗滑桩采用弹性模型，密度为2.5 t/m3，杨氏模量为42.6 GPa，泊松比为0.2。

拟采用条分法计算滑坡的最大下滑力，从而确定抗滑桩的布设位置。如图2，首先将坡体等距分为五块土条，然后计算各土条的剩余下滑力。根据计算，本文将抗滑桩设置在土条3及土条4之间。

图2 条分法计算图

3 抗滑桩精细化模型

3.1 材料参数及本构模型

通过边坡模型的计算可以得到抗滑桩桩顶的水平位移时程，该位移时程作为输入荷载施加在抗滑桩精细化模型顶部，即实现了桩土分离建模，精简了计算量。如图3，抗滑桩直径为1.2 m，桩长为12 m。等圆心角布置八根直径为25 mm的HRB335钢筋。

图3 抗滑桩精细化模型

对于中柱精细化模型，仍采用Mohr-Coulomb模型来描述土的变形特征。中柱结构延用混凝土塑性损伤模型，中柱内纵向受力钢筋采用Mises理想弹塑性本构模型，其中ρ=7.8 g/cm3、E=200 GPa，泊松比为0.1，屈服应力为335 MPa，采用内置区域方式与主体结构连接。根据混凝土结构2010年设计规范[18]，模型采用的混凝土单轴受压行为，如图4所示。

图4 混凝土单轴受压应力-应变曲线

曲线与中柱一样参照混凝土结构2010年设计规范[18]进行取用。

图5 混凝土单轴拉伸应力-应变曲线

此外，在混凝土塑性损伤模型中还有一个需设参数为塑性损伤因子，在混凝土结构2010年设计规范中也有明确的定义以及计算公式，由于开裂后混凝土结构中的拉伸应力主要由钢筋承担，混凝土单轴拉伸行为曲线取为线性，所以无需定义拉伸行为的损伤因子。记压缩损伤因子为dc，其定义为：

(1)

式中：E0为初始弹性模量，Ec为压缩状态下卸载路径的弹性模量。

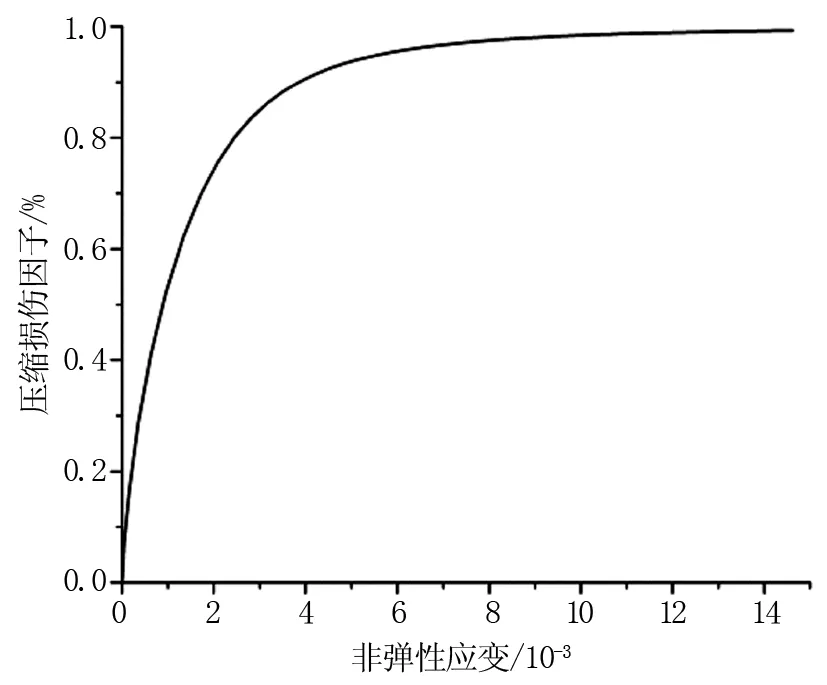
图6 压缩损伤因子曲线

3 结果分析

3.1 不同治理方式模拟结果

图7为不同治理方式下计算得到的安全系数以及坡顶水平位移的发展情况。从安全系数来看，削坡后计算得到的安全系数最大，为1.442 09；按方案布设抗滑桩的边坡模型计算得到的安全系数次之，为1.339 36；天然边坡模型计算得到的安全系数最小，为1.228 84。取得安全系数的时刻均为模型终止计算的时刻，若取桩顶位移发生突变的时刻读取安全系数，则具体数值上还会有微小的变化，但大小关系不会改变。抗滑桩的安全系数较之天然边坡未发生大幅度的提升，推测其原因应该有以下几个方面。

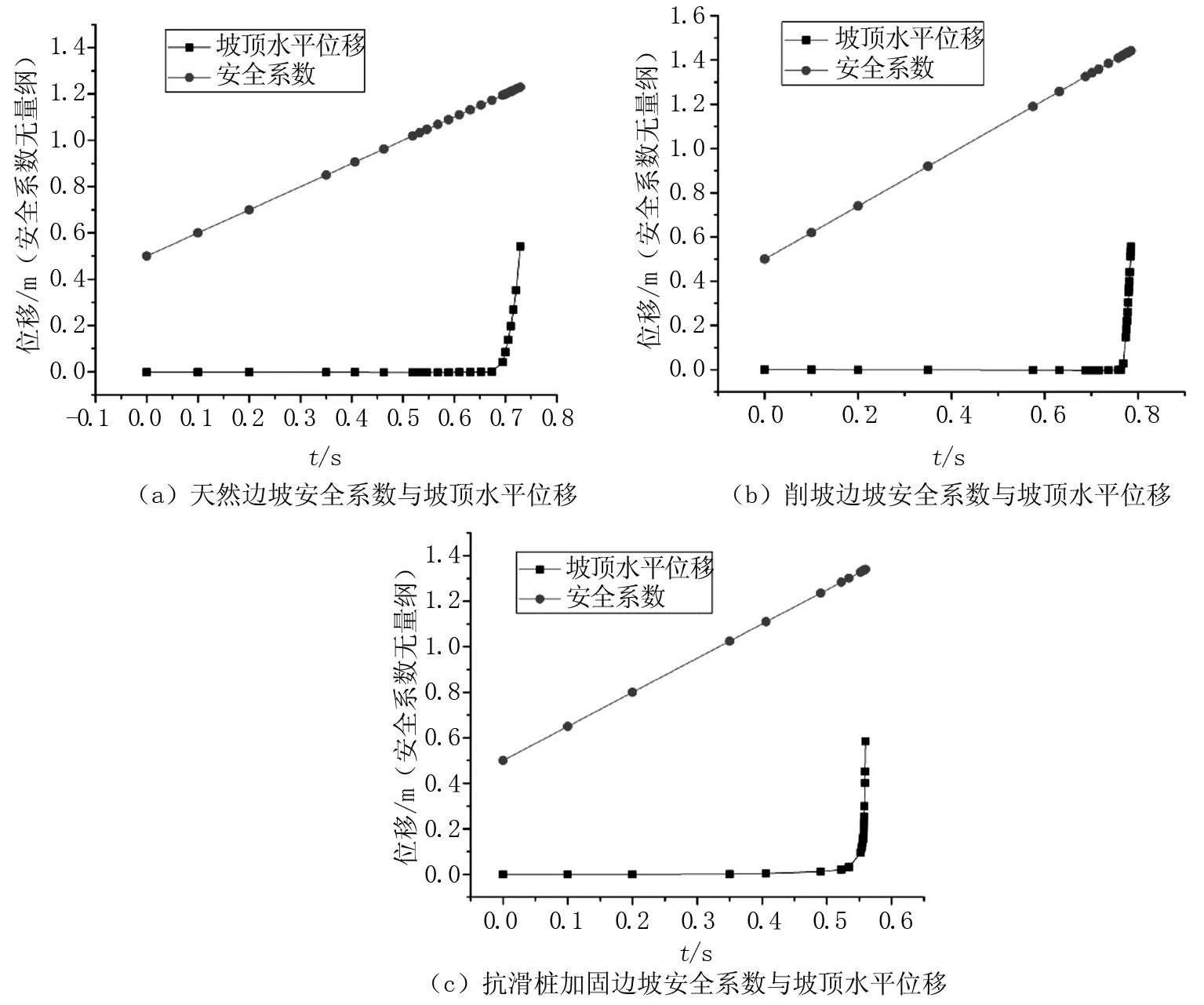
图7 安全系数与坡顶水平位移

首先，抗滑桩的嵌固深度为按经验取值，未像确定桩位一样进行严密的计算推导，所以距离最佳嵌固深度有一定的差距。其次，所建立的模型中， 土层进行了均一化处理， 其弊端就是整个边坡都处在松散土层，抗滑桩实际并未嵌入稳定、坚固的土层，仅在底部进行了约束，导致计算中桩体随松散土层一并发生位置的变化，料想并未充分发挥其强度。边坡模型中抗滑桩桩顶的水平位移时程曲线如图8所示。

图8 抗滑桩桩顶水平位移

从各模型计算得到的累积塑性应变云图可以看到，削坡后边坡的塑性区位置较之于天然边坡发生了一定的后移，整体开展形式较为类似。而经过抗滑桩加固边坡的塑性区开展则与前者的分布形式有所不同，桩前后的土体，其塑性应变的发展程度截然不同，桩体前后的塑性区无法贯通，换言之，边坡未发生整体性的失稳，由此可见虽然同样最终边坡发生了失稳，但滑坡的形式与体量有所差异，抗滑桩的存在一定程度上限制了坡体内塑性区的发展，从而减小了滑坡体的体量，提高了边坡的安全系数。

3.2 抗滑桩精细化模拟结果

将图8的桩顶位移时程作为输入荷载施加在模型(图7(a))顶部，得到了滑坡发展过程中，抗滑桩的受力变化情况。从计算终止时桩体的等效塑性应变云图，可以看到塑性应变累积的位置与的钢筋发生应力集中的位置大致是吻合的，实际进行工程设计时，应该对这一位置进行重点设防，增加横向约束钢筋的用量，从而保证抗滑桩在工作中不发生破坏。虽然在图示位置塑性应变有所累积，但其幅值并不是很大，甚至未达到所用混凝土的开裂应变，其中有抗滑桩参数设置不当的原因，也有模拟流程不到位的原因，对抗滑桩进行精细化模拟时，未能考虑桩身周围土体的影响，所以计算结果存在较大误差。

4 结 论

本文通过Abaqus建立了天然边坡、经削坡处理后的边坡以及布设抗滑桩的边坡模型，通过计算得到了各模型下的安全系数；通过对抗滑桩进行精细化建模，将桩土模型计算得到的桩顶位移施加在精细化模型上，研究了抗滑桩在滑坡发生过程中的响应特性，并找出了桩身应力集中的位置。虽然模型精度及参数选取存在一定的误差，但结果仍可以反应各治理方式的有效性。抗滑桩的精细化建模虽然仍有诸多不足之处，但思路正确，在未来的研究中可以继续完善、应用。研究结论如下。

(1)模拟结果表明，在本文采用的防护方案下，边坡安全系数从高到低排列依次为：削坡后的边坡、抗滑桩加固后的边坡以及未作任何处理的天然边坡。

(2)抗滑桩对坡体内塑性区的贯通有较为显著的抑制作用，且通过条分法可以确定最佳桩位，通过计算也可以得到合理的桩长和配筋量，是十分有效的滑坡治理手段。

(3)通过对抗滑桩的精细化建模可以得到桩身塑性应变累积以及钢筋发生应力集中的位置和时刻，针对这些区域进行重点设防，增加横向约束钢筋的用量，可以增加桩体的抗性。

(4)本次模拟虽有诸多考虑不足之处，但整体思路大致正确，在今后的研究学习中可以继续完善并应用于实践中。