结合超混沌系统和Logistic 映射的视频图像加密算法

韦丞婧，李国东

（桂林电子科技大学数学与计算科学学院，广西桂林 541010）

0 概述

在互联网技术不断发展、信息传递越发频繁的时代，各种形式的信息在网络上的传输极大地方便了人们的生活与工作。但在图像和视频的传输过程中，这些信息往往容易遭到非法窃取、篡改和传播，造成数据泄露，信息的安全得不到保障［1］，尤其是在军事、航天、医学等一些关键领域，图像和视频信息的泄露可能会造成不可估量的损失。

混沌系统因具有确定性、随机性、初值敏感性、遍历性等特点［2］，在图像加密算法设计中得到广泛运用［3］。同时，目前对混沌系统理论的研究也不断深入［4-7］。

在图像加密设计研究中，研究者提出了许多针对单幅图像的加密算法设计。文献［8］提出了改进的Logistic 映射方法，运用置乱-扩散同时操作的方式对图像进行加密。文献［9］提出了一种对多图像重组加密的算法，运用L-F 级联混沌生成混沌序列，实现了对多幅不同尺寸的图像进行加密。文献［10］提出由Logistic映射改进的复合混沌系统，设计了一种新的S 盒运用于加密。一维混沌映射简单直接，能够快速生成混沌序列，提高加密的速度，但其参数少且形式简单，容易遭到穷举攻击。文献［11］在使用低维混沌映射的基础上，提出结合动态DNA 编码加密的算法，但根据混沌序列对图像分块选取不同DNA 编码规则增加了加密用时，效率不高。文献［12］在一维Logistic 混沌映射的基础上进行改进，扩大了混沌序列取值的范围，但该方法参数少，密钥空间较小。文献［13］提出使用混沌系统与压缩感知的方法对图像进行加密，增加了算法的复杂度，但由于加密过程有损，尽可能降低图像质量损失的方案设计较困难。

高维混沌系统具有复杂的动力学特性，而低维混沌系统应用在加密中安全性不足，这是因为低维混沌系统虽有正的李雅普诺夫指数，但值不够大，且容易发生简并，导致混沌动力学特性退化。同时，低维混沌系统的可变参数较少，导致密钥空间不大，无法抵御穷举攻击［14］。文献［7］提出运用细胞神经网络（Cellular Neural Network，CNN）混沌系统和Lorenz 混沌系统进行双扩散加密的方法，增加了加密算法的复杂度和密钥空间，但高维混沌系统结构复杂，增加了计算用时［1］，难以对信息量较大的视频图像进行加密。对于多图像的加密方案设计，文献［15］将多幅图像转换成二维码的方式，根据光学加密原理进行组合加密，实现了对多幅图像的快速加密，提高了效率，但图像转换二维码过程复杂，在实际应用中难以实现。在对视频加密的研究中，部分研究者提出对视频进行选择性加密的方法。文献［16］提出了先对视频码流进行分析选择，再对选取的部分进行加密的方法，节省了视频加密所需要的时间。然而，这一类视频加密算法在加密过程中需要对视频进行压缩，这会对原视频质量产生影响，因而所设计的加密方案不是无损的。

针对以上问题，本文提出一种视频帧逐一加密与组合加密相结合的视频图像加密算法。对视频帧逐帧加密，采用计算速度较快的Logistic 混沌映射，对每帧图像使用哈希函数生成哈希值，计算控制每帧加密对应的混沌序列初值，生成混沌序列，再对视频帧进行逐一异或，达到一帧一密的效果。在此基础上，将所有视频帧进行组合，采用动力学特性更为复杂的六维细胞神经网络混沌系统生成混沌序列，根据混沌序列对组合矩阵进行置乱扩散，再分解为单帧图像完成加密。

1 混沌系统

1.1 神经网络混沌系统

1988 年，细胞神经网络（CNN）首次由CHUA 等提出［17］，其以细胞为基本单位，是一种局部互联的神经网络系统。由M行、N列个细胞排列组成的细胞神经网络系统定义如下：

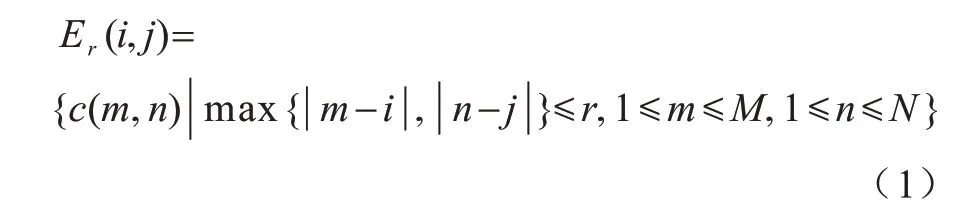
其中：Εr(i,j)为半径为r的第i行第j列的细胞的邻域；c(m,n)为邻域内的细胞。

细胞的状态方程可表示如下：

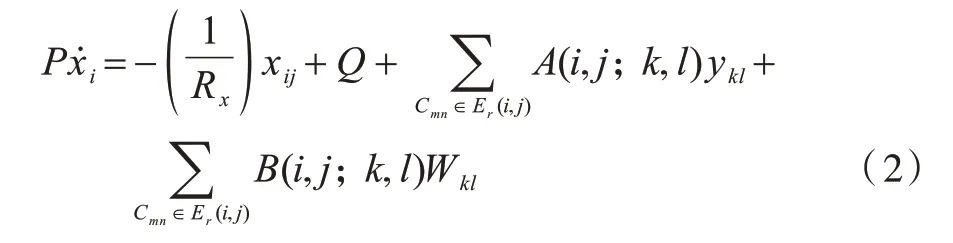
输出方程表示为：

其 中：|Wkl| ≤1,|xij(0)| ≤1,P＞0,Rx＞0；Q为阈值 常数；yij为输出变量；P为线性电容；Rx为线性电阻；A为反馈模板；B为控制模板。

研究表明，高维超混沌系统拥有更优良的混沌特性。因此，本文选用六维细胞神经网络混沌系统，其表达式如下［18］：

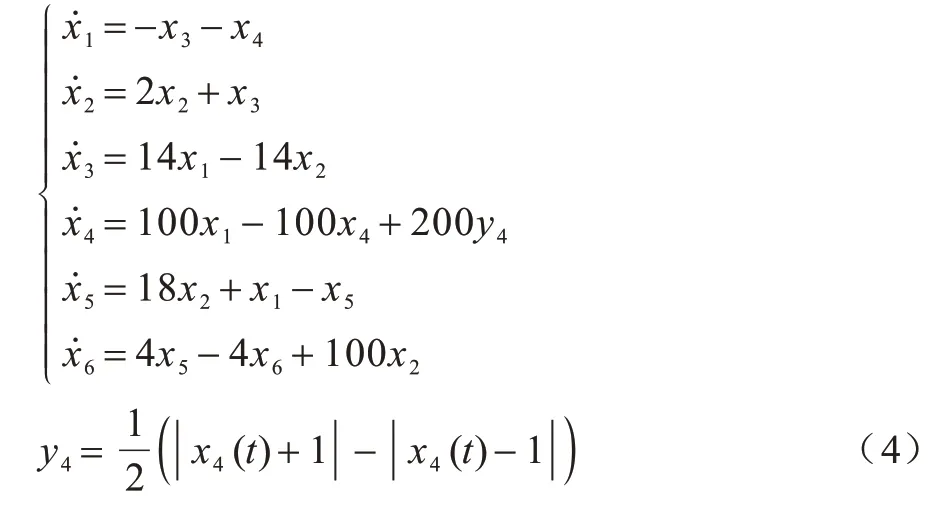
计 算Lyapunov 指 数，当t→∞时，λ1=2.748 1,λ2=-2.984 4,λ3=1.241 1,λ4=-14.454 9,λ5=-1.412 3,λ6=-83.228 2,其中有2个正的李雅普诺夫指数，说明系统是超混沌系统。相比于仅使用一个一维混沌映射产生的6个混沌序列，使用六维CNN 混沌系统产生的6个混沌序列动力学特性更复杂，随机性更高。因为具有2 个及以上正的李雅普诺夫指数的混沌序列表明混沌轨道能够从多个维度产生分离，从而增加了不同序列间数值的随机性。

1.2 Logistic 混沌映射

Logistic 混沌映射是最简单的一维混沌映射。1995 年，PHATAK 对Logistic 混沌映射的混沌特性进行了研究［19］，给出其表达式为：

其 中：Xn∈(0,1),n=1,2,…。经研究表明，当μ∈[3.569 945 627,4]时，序列Xn处于混沌状态。该一维混沌序列计算形式简单，且有很好的伪随机序列特性，被广泛运用于图像加密中。

2 伪随机序列发生器设计

获取混沌序列首先需要确定初始值［20］。根据混沌系统的初值敏感性，当初值仅发生微小变化时就会使得混沌序列的数值发生很大的变化。因此，在本文算法中，对视频每隔固定帧数选取一个视频帧，利用哈希函数生成该视频帧图像信息的摘要，并根据摘要信息计算更新伪随机序列的初值，以用于对视频的逐帧加密。将每次加密所用到的混沌系统的初值作为密钥，使得算法的密钥与视频明文图像相关，所需要加密的视频图像不同，产生的密钥也不同。

2.1 逐帧加密的伪随机序列发生器

将短视频按帧分成s张尺寸都为M×N的图像，间隔f帧更新一次混沌序列的初值，根据第1+nf(n=0,1,…；1+nf≤s)帧图像的像素矩阵，使用SHA-256 哈希函数生成256 位二进制表示的哈希值L1+nf：

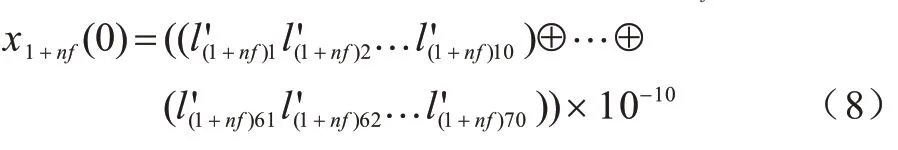
将初值代入到Logistic 混沌系统中，迭代100+MN-1 次，去掉前100 个值得到混沌序列x1+nf(t),t=101,102,…,100+MN-1，再将混沌序列转换成取值范围在［0，255］之间的数：

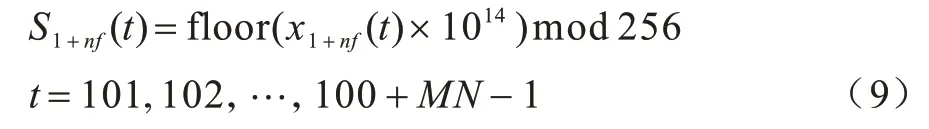
2.2 组合加密的伪随机序列发生器

将s个M×N的像素矩阵转成二进制，组合成一个MN×8 的矩阵，根据组合矩阵使用SHA-256 哈希函数生成256 位哈希值C：

将KC 转化成十进制数C′：

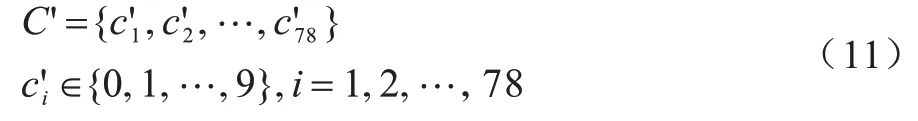
从C′中从左到右取，每10 位数字组成一个数，共取60 位，再分别乘以10-10得到混沌序列的初值x(0)={x01(0),x02(0),x03(0),x04(0),x05(0),x06(0)}。

将x(0)代入六维CNN方程中，迭代100+M×N-1次，生成6 个混沌序列，去掉前100 个值，得到x(t)={x1(t),x2(t),x3(t),x4(t),x5(t),x6(t)},t=101,102，…，100+MN-1。对混沌序列做以下处理，将序列的取值范围变成［1，M×N］：

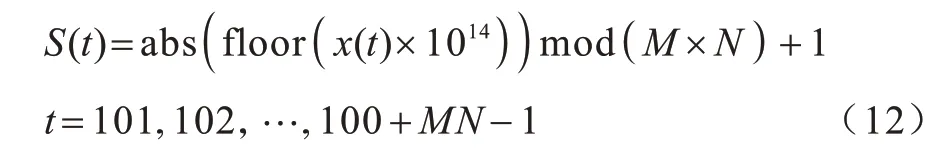
3 多帧图像组合方法设计

本文对多帧图像组合的方法采用类似于计算机使用二进制储存信息的方式。例如，十进制数11 和其二进制形式1011 之间相互转换的规则为：

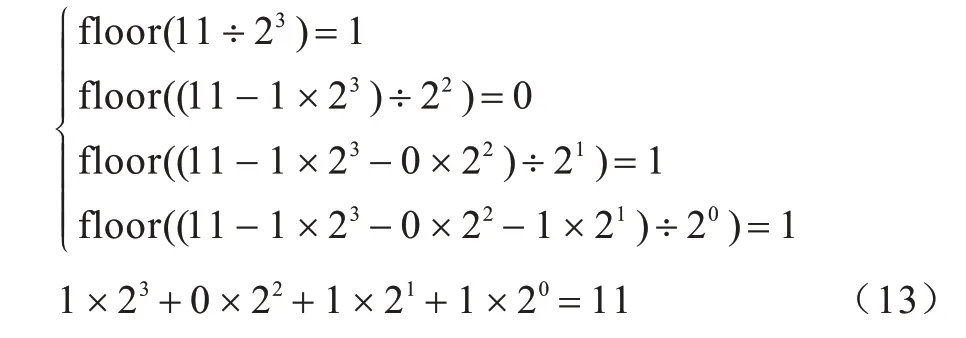
同样地，设视频共有s帧，将视频帧I={I1,I2,…,Is}转换成 二进制，得 到是M×N行8 列、元素取值为0 或1 的矩阵，再做以下运算得到组合矩阵P：

由于组合矩阵的每一行表示所有视频帧在相同位置的像素值，因此对组合矩阵进行置乱不仅会改变像素点的值，也会改变像素点的位置。

对组合矩阵P再按十进制转二进制的方式，可以重新分解成s个M×N行8 列的二进制矩阵：

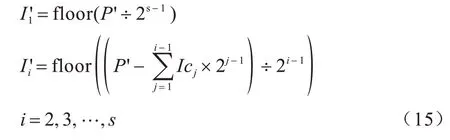
4 图像加密

以灰度视频图像为例，完整的加密步骤描述如下：

1）将视频按帧分成s个M×N的图像像素矩阵。

2）设置更新Logistic 混沌初值的帧间隔f，对第1+nf(n=0,1,…；1+nf≤s) 个像素 矩阵分 别使用SHA-256 哈希函数生成图像的哈希值，经过2.1 节所描述的算法计算得到加密第1+nf帧到第(n+1)f帧图像对应的Logistic 混沌序列的初值x1+nf(0)，代入Logistic 混沌系统迭代得到n+1 个混沌序列x1+nf(t)，并将序列按式（9）处理成取值范围为［0，255］的伪随机序列S1+nf(t)。

3）将Logistic 混沌序列S1+nf分别与第1+nf帧～第(n+1)f帧图像像素矩阵I1+nf,I1+nf+1,…,I(n+1)f按位异或，最终得到经过逐帧加密的视频帧。

5）对组合矩阵P按照2.2节所述方法，使用SHA-256函数生成组合矩阵的哈希值C，经过计算得到CNN混沌系统的初值x(0)，代入CNN 混沌系统迭代得到6 个混沌序列x(t)，并将序列按式（12）处理成取值范围为［1，M×N］的伪随机序列S。

6）按从左到右、从上到下的顺序将P(i,j)的值与P(u,ν)的值互换，其中u，ν计算公式如下；

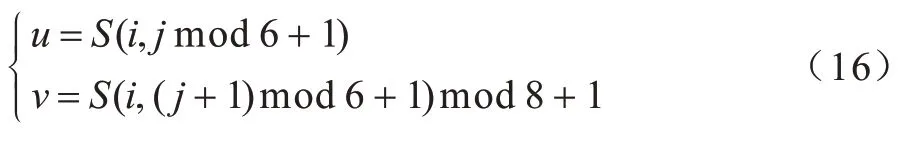
7）将替换后的组合矩阵按式（15）重新分解为s个二进制矩阵Ei(i=1,2,…,s)，转回十进制表示形式，即得到s帧加密视频帧

由于本文设计的加密算法为无损加密算法，因此解密过程即为加密过程的逆过程。将加密步骤用流程图表示，如 图1 所 示。其 中：L1+1×f、L1+2×f、L1+n×f和C1、C2、C[s/52]+1分别为根据视频帧、组合矩阵使用SHA-256生成的哈希值；x1+i×f(0)为第1+i×f(i=1,…,n)帧图像对应的Logistic混沌序列的初值；x1(0),x2(0),x[s/52]+1(0)为CNN 混沌序列的初值，S1+i×f(t)为第1+i×f(i=1,…,n) 帧图像 对应的 Logistic 混沌序 列；S1(t),S2(t),S[s/52]+1(t)为对应的CNN 混沌序列。

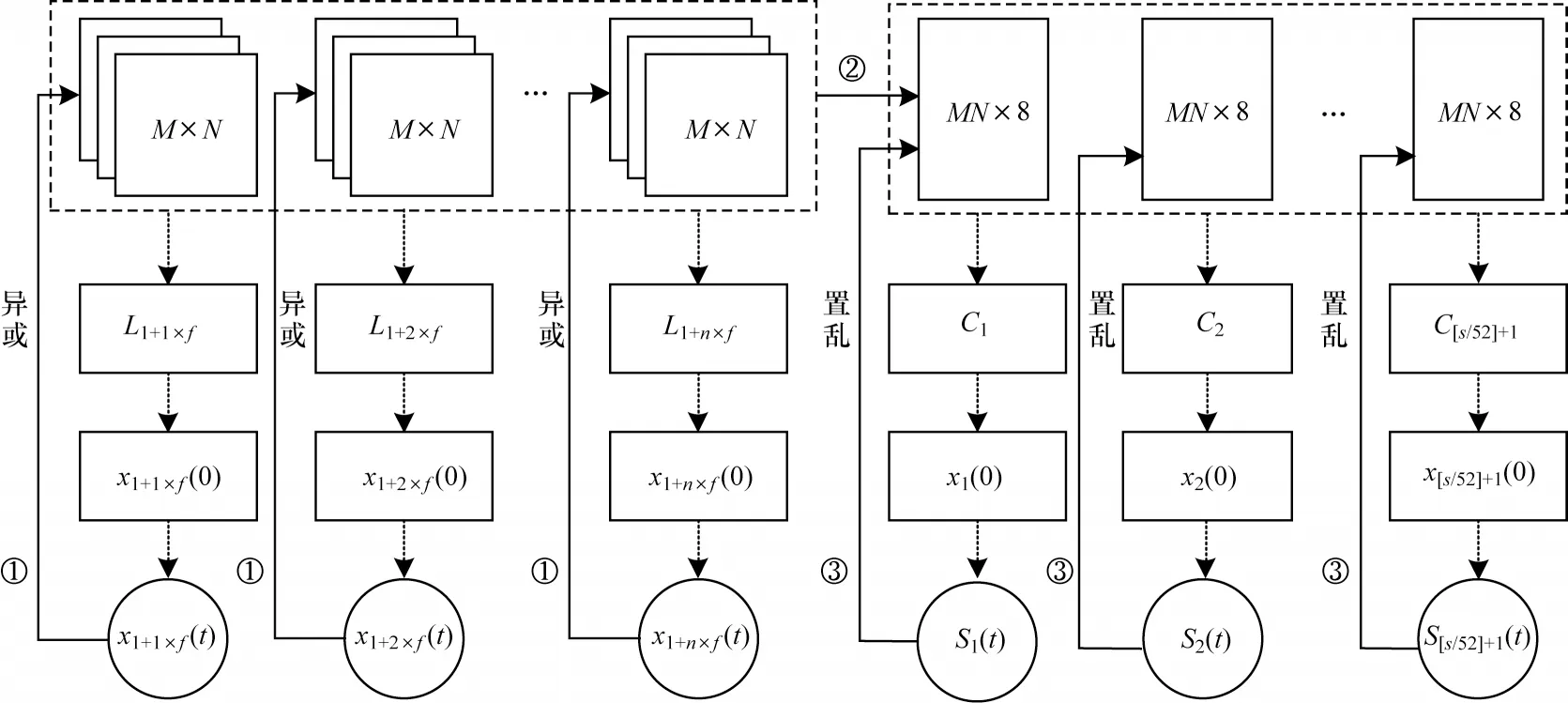
图1 加密流程Fig.1 Encryption process

5 实验仿真和安全性分析

选取2 个320×240 视频的前12 帧图像作为仿真实验中需要加密的图像。在逐帧加密中，对每一帧图像都更新Logistic 混沌序列的初值，即更新初值的帧间隔f=1。将本文算法中六维CNN 混沌序列改为初值不同、参数相同计算生成的6 个Logistic 混沌序列，同样对视频图像进行加密，比较两种加密方案的安全性能。经过本文算法加密，分别得到2 个视频图像中第6、12 帧的明文图像、加密图像和解密图像，如图2、图3 所示。

图2 视频A 部分帧加密和解密结果Fig.2 Encryption and decryption results forpartofframes ofvideoA

图3 视频B 部分帧加密和解密结果Fig.3 Encryption and decryption results for part of frames of video B

5.1 信息熵分析

信息熵是对信息量的量化度量，信息熵越接近8，表示图像所含信息量越小，随机性越强。本文计算了视频A 和视频B 每帧图像加密前后的信息熵，如表1 所示。表2 给出了视频A 加密后平均每帧的信息熵，和仅使用一维Logistic 混沌映射进行加密、其他文献提出的图像加密算法做比较。

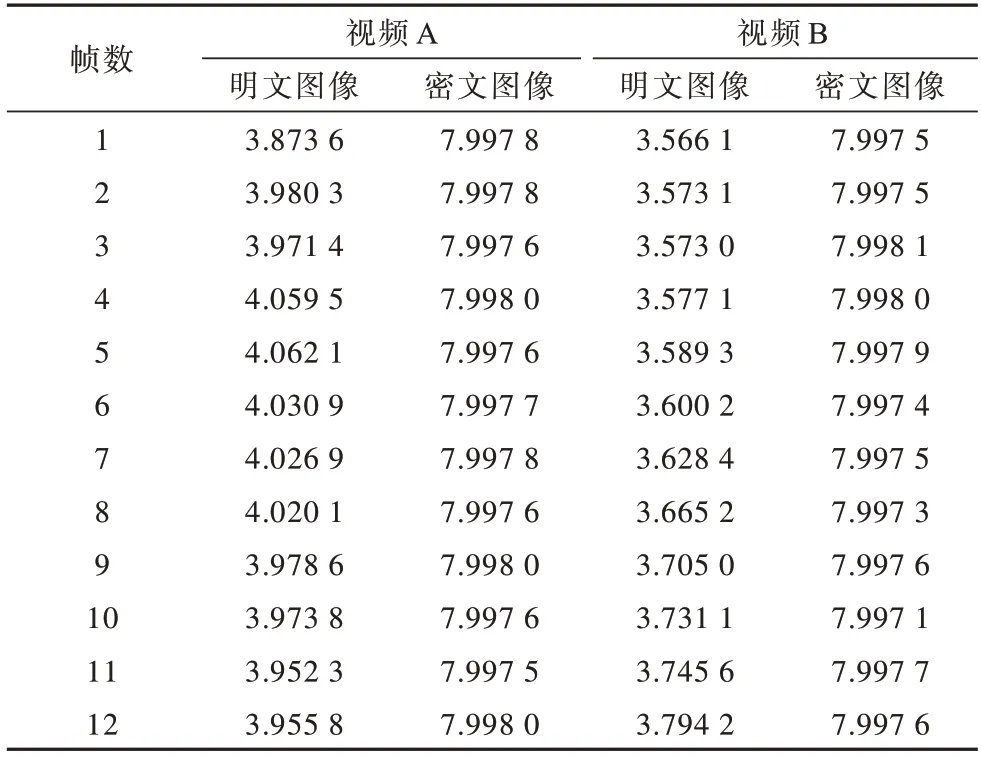
表1 视频帧加密前后信息熵Table 1 Entropy of video frames before and after encryption

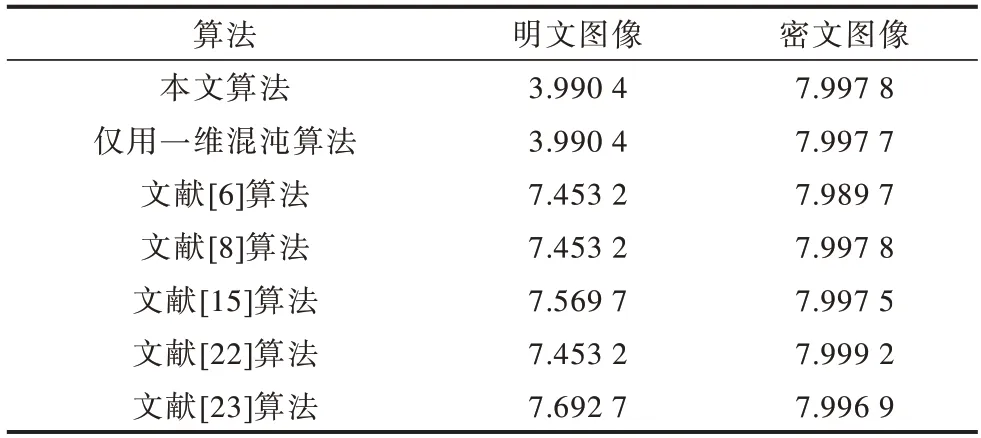
表2 不同加密算法的信息熵比较Table 2 Entropy comparison of different encryption algorithms

由表1 和表2 可以看出：经过加密后视频帧的信息熵皆达到了7.997，加密效果较好；本文的算法相比于其他算法加密的信息熵处于较高水平，且相比于仅用一维混沌加密得到的信息熵更高一些。

5.2 密钥空间分析

在本文设计的算法中，所用的Logistic 混沌映射的1 个参数和6 阶CNN 超混沌系统的78 个参数可作为密钥，计算精度为计算机所能达到的精度10-14；在逐帧加密中，将每次更新得到的Logistic 映射的初值作为密钥，算法中精度为10-10，可根据实际需要调整更新初值的间隔帧数，间隔越大，密钥个数越少；在组合加密中，每个组合矩阵所对应的CNN 混沌系统的6 个初值作为密钥，精度同样为10-10。在本文的仿真实验中，密钥空间可以计算为1014×79×1010×12×1010×6=101286。本文算法密钥空间足够大，能够抵御穷举攻击，且能够根据实际加密需要调整密钥个数，提高加密效率。

5.3 密钥敏感性分析

在图像加密中，密钥的敏感性是评价加密算法是否安全的一个重要指标。当算法的密钥仅发生微小变化，就能导致使解密失败，从而很好地抵御攻击。在本文实验中，将生成第1 个Logistic 混沌的初值减小，再对密文图像进行解密，得到第3 帧的解密图像，如图4 所示。可以看出，本文提出的算法密钥敏感性较强。

图4 改变密钥进行解密结果图Fig.4 Decryption results of changing key to ecrypt

5.4 抗差分攻击能力分析

破译者选用对指定像素点的值进行改变的不同明文图像，对同一加密算法进行加密，通过分析每次加密后图像之间的关联与差别总结出加密算法，能够达到破译的目的。若明文图像改变像素点的值后密文图像像素点的值随之改变，则能很好地抵抗差分攻击。NPCR 和UACI 指标能衡量密文图像的抗差分攻击能力，计算公式如下：

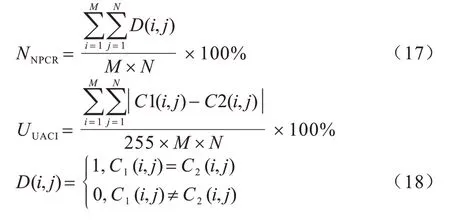
其中：C1(i,j)和C2(i,j)分别为明文图像和更改了一个像素点的值的明文图像经过同样加密算法加密后第i行第j列的像素值。

在仿真实验中，分别将视频A 和视频B 第3 帧明文图像第80 行第100 列的像素值改为0，经过加密后计算图像更改像素值前后的NPCR 值和UACI 值，并和仅使用一维Logistic 混沌映射进行加密、其他文献加密算法进行比较，结果如表3 所示。可以看出，仅仅更改其中一帧图像的一个像素点的值，就能使每一帧的密文图像大部分像素值都发生变化。加入CNN 高维混沌系统进行加密的UACI 值有更好的表现，说明本文的加密算法较好。

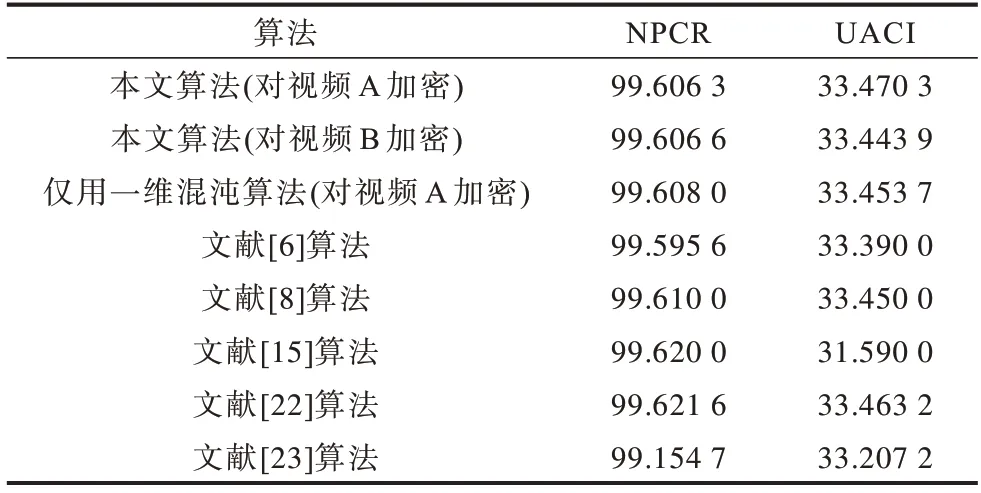
表3 视频帧NPCR 和UACI 的值Table 3 NPCR and UACI of video frames

5.5 抗剪切攻击能力分析

视频图像在传输过程中还容易遭到剪切攻击，导致部分数据丢失的情况［8］。本文实验测试视频A丢失1/4、1/2 的数据时解密的效果。图5 为解密前后第3 帧的图像，可以看到，解密后的视频帧仍能基本还原图像，肉眼能够分辨得出图像内容，说明本文算法的抗剪切攻击能力较强。

图5 视频A 第3 帧丢失部分数据解密效果Fig.5 Decryption of the third frame of video A with partial data missing

5.6 直方图分析

分别绘制视频A 和视频B 的第6 帧、第12 帧明文图像、密文图像直方图，如图6 所示。可以看出，视频帧原图像直方图分布及不均匀，呈现出了明显的规律，经过加密后像素点基本能在［0，255］范围内均匀取值。

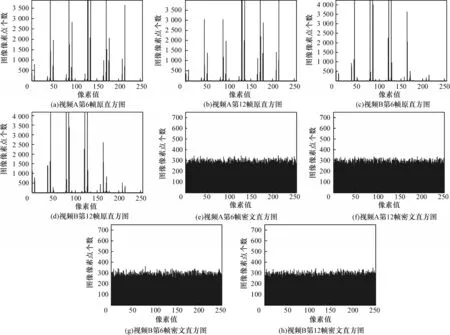
图6 视频加密前后直方图Fig.6 Histograms of video frames before and after encryption

5.7 相邻像素点相关性分析

明文图像的相邻像素点通常具有较高相关性，相关系数接近于1。对图像进行加密需要消除这种相邻像素点间的相关性，才能很好地抵抗统计攻击。本文对视频A 和视频B 每一帧都在水平、垂直、对角3 个方向上计算其相关系数，结果如表4、表5 所示。可以看出，经过本文加密后像素点相关系数都接近于0。

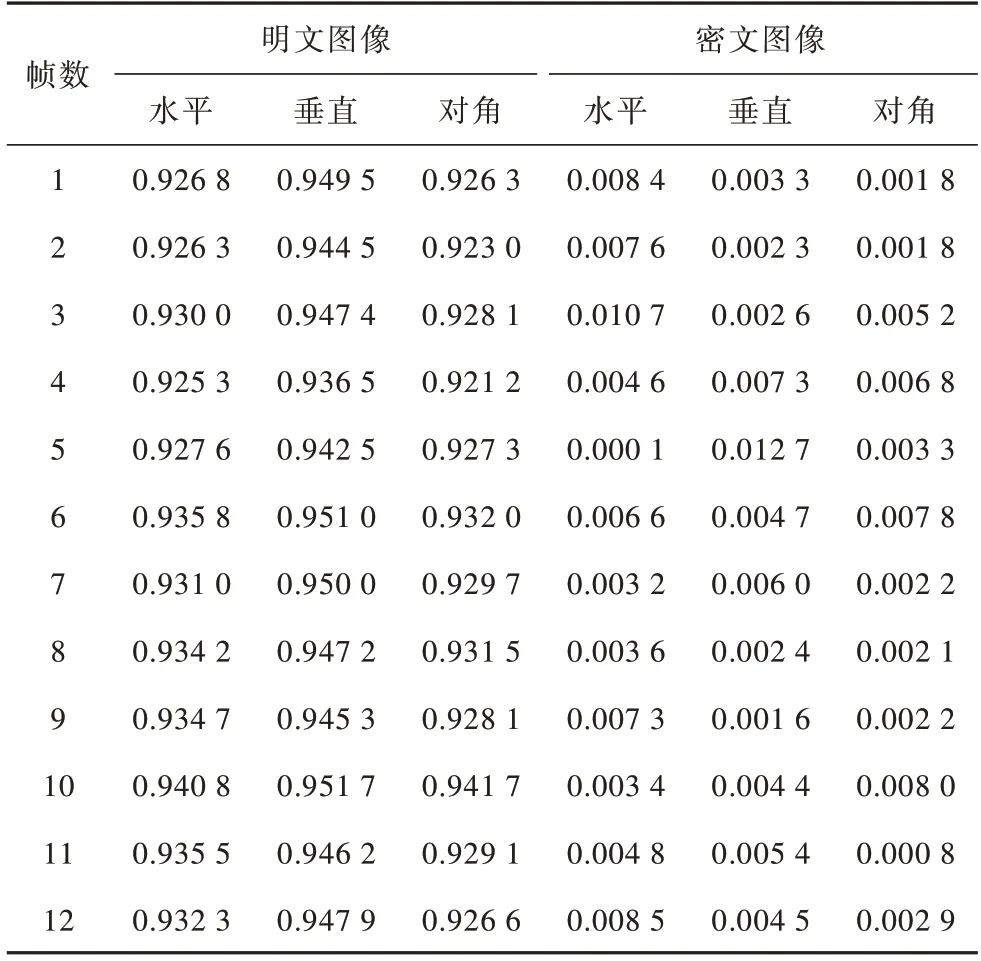
表4 视频A 每帧相邻像素点相关系数Table 4 Correlation indexes between adjacent pixels of video A

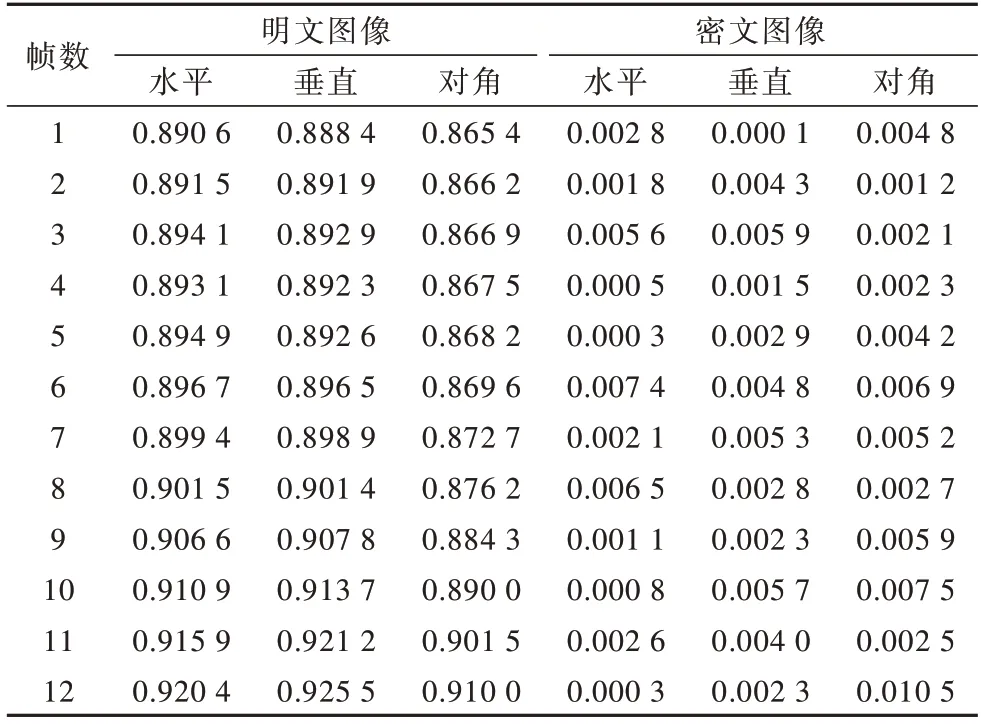
表5 视频B 每帧相邻像素点相关系数Table 5 Correlation indexes between adjacent pixels of video B

表6 给出了仿真实验中视频A 加密后平均每帧相关系数，和仅使用一维Logistic 混沌映射进行加密、其他文献提出的图像加密算法进行比较。可以看出，本文算法平均每帧相关系数最低达到0.003 749，很好地消除了像素点间的相关性，且使用CNN 高维超混沌系统生成序列进行加密后像素点间的相关系数更低。

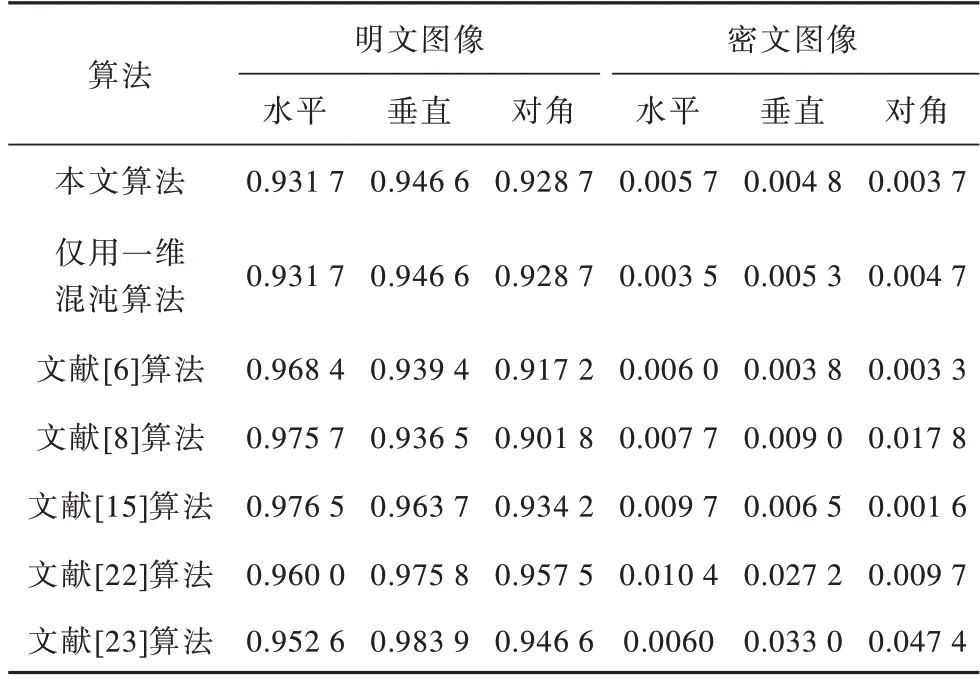
表6 相邻像素点相关系数比较Table 6 Comparison of correlation coefficients between adjacent pixels

选取视频A 和视频B 的第3 帧，分别绘制加密前后在水平、垂直、对角3 个方向上相邻像素点的散点图，如图7、图8 所示。可以看出，视频帧明文图像的相邻像素点散点图呈线性趋势，而加密后的散点图均分布均匀。

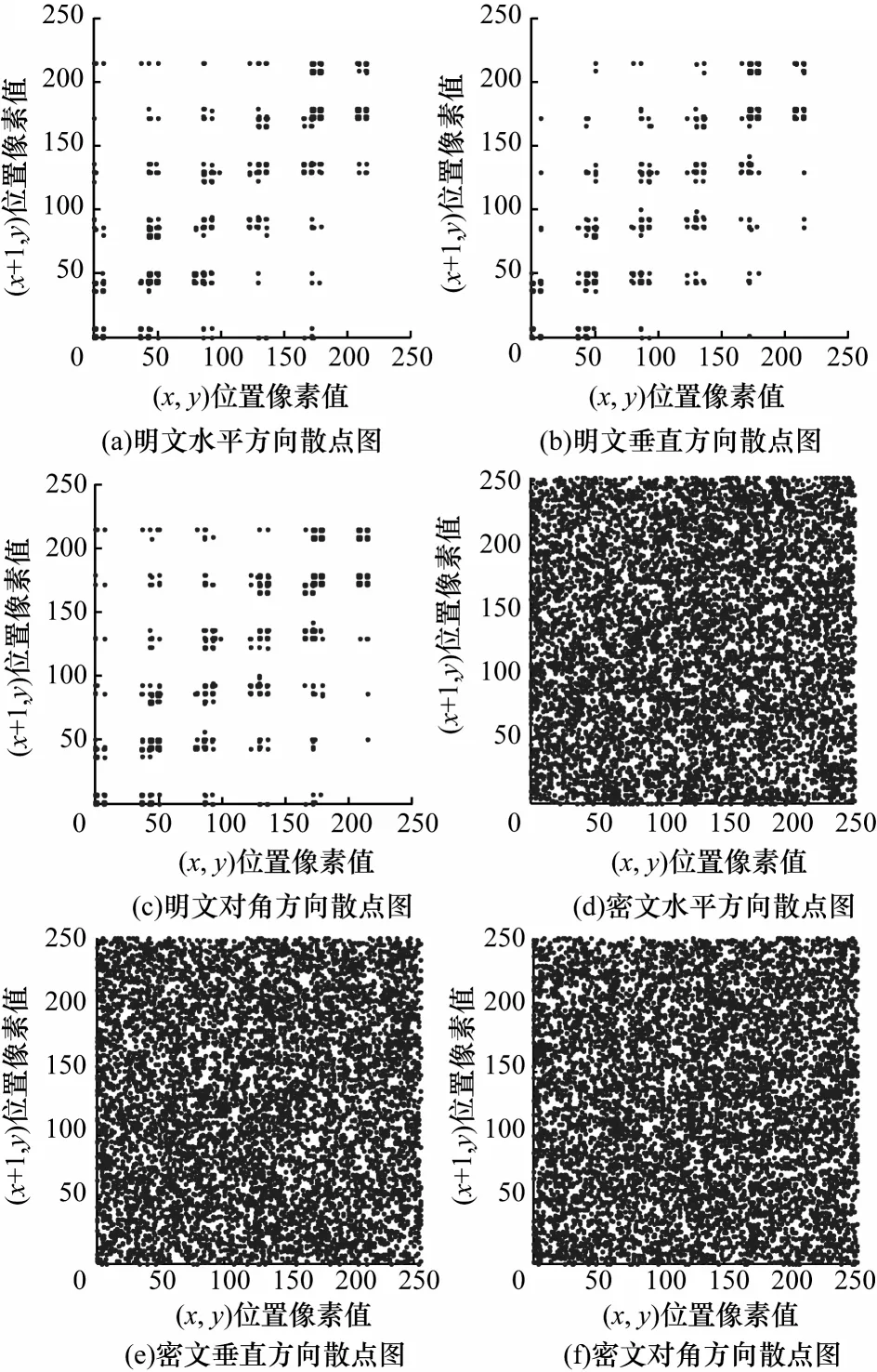
图7 视频A 第3 帧加密前后相邻像素点散点图Fig.7 Adjacent pixel scatter plot of the third frame of video A before and after encryption

图8 视频B 第3 帧加密前后相邻像素点散点图Fig.8 Adjacent pixel scatter plot of the third frame of video B before and after encryption

6 结束语

本文提出一种对视频帧图像逐一加密、组合加密相结合的视频加密算法。利用结构简单的一维Logistic 混沌序列逐帧加密，通过随机性较强的六维CNN 混沌序列对视频帧组合矩阵进行置乱。仿真实验结果表明，该算法引入具有复杂动力学特性的高维混沌系统，安全性能相比于仅使用一维混沌的算法要高，且具有较好的稳定性，同时算法复杂度和密钥个数可根据需要灵活改变，能适应不同的视频长度和不同的加密安全需要。此外，设计的组合加密方法能够通过一轮操作实现像素点位置和取值同时改变，提高了加密算法的效率。相比于单幅图像的加密，本文算法对视频按帧进行加密，所需要处理的数据量更大，更适用于对包含重要信息的短视频进行加密。后续将把算法推广到对时长更长、清晰度更高的视频进行加密，并进一步提高加密效率。