基于LightGBM-LSTM的公交到站时间预测

罗建平，陈 欢，杨森彬，张燕忠

(1.广东省城市智能交通物联网工程技术研究中心，广州 510663;2.广州交信投科技股份有限公司，广州 510663)

0 引言

实时公交到站预测是城市公交排班调度的重要依据，也是影响乘客出行体验的重要因素，具有重要的社会意义和价值。如果公交车辆到站预测时间不准，将可能产生公交车辆调度断位、发班不均匀等问题[1-3]，进而影响乘客出行服务体验。

国内外相关领域的专家和学者在公交到站时间预测方面做了诸多研究。Tirachini[4]等考虑了城市不同区域道路环境对公交车行程时间的影响，采用多元线性回归模型对公交到站时间进行了预测；Huang[5]等基于贝叶斯模型预测短期公交出行时间；霍豪[6]等虑上下游车站的距离、信号灯数和弯道数，基于KNN算法提高到站时间预测的准确性和稳定性；童小龙[7]等采用改进的时间序列法进行公交车辆站间行程时间预测，增强对于突发事件的反应能力；赖永炫[8]等采用时空相关属性模型进行公交到站预测，模型准确率为80.23%;李鹏程[9]等考虑公交到站前2～3站的信息，用两层LSTM模型对公交到站时间进行预测；玛尔然[10]建立公交车在路段上的运行时间、站点停靠时间、交叉口延误时间的时间模型，采用卡尔曼滤波递推方程预测公交到站时间，模型的准确率可达到90%以上。

现有关于公交到站时间预测的研究普遍存在准确性和稳定性不高的问题。由于城市公交出行呈现明显的早晚高峰现象，本文提出了一种基于LightGBM-LSTM的公交到站时间预测方法，考虑了影响公交到站时间的重要因素，如车辆实时位置、时间特征、高平峰状态等。首先采用LSTM算法对高平峰状态进行有效识别；然后采用LightGBM算法进行公交到站时间预测，并给出了模型的评价指标；最后以广州市某典型公交线路为例进行实验，结果表明基于LightGBM-LSTM的方法具有良好的预测效果。

1 公交到站时间预测模型

图1是基于LightGBM-LSTM的公交到站时间预测算法总体架构，包括三大模块：一是数据采集与预处理模块，从公交调度系统中提取历史数据集，经过数据预处理划分为训练集和测试集，用于模型训练和测试；二是分类和预测建模模块，首先采用LSTM算法构建高平峰模式识别模型，其输出作为到站时间预测模型的一个输入特征，然后采用LightGBM算法构建到站时间预测模型；三是模型预测模块，基于车辆实时信息封装到站预测服务接口。

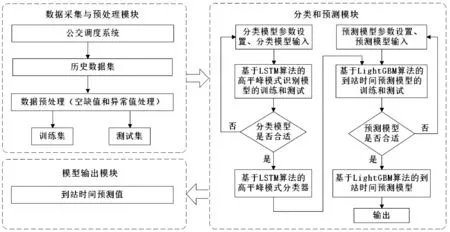
图1 基于LightGBM-LSTM算法的公交到站时间预测算法总体架构

1.1 基于LSTM的高平峰模式识别模型

1.1.1 LSTM工作原理

LSTM算法是一种RNN(循环神经网络)算法。LSTM算法对RNN网络的改进在于其在每一个判断元胞中放置了四扇阀门(输入阀门、遗忘阀门、更新阀门和输出阀门)，阀门的开闭状态能够用来判断模型的记忆结果是否达到加入到当前层的计算中的阈值。LSTM基本网络架构如图2所示。

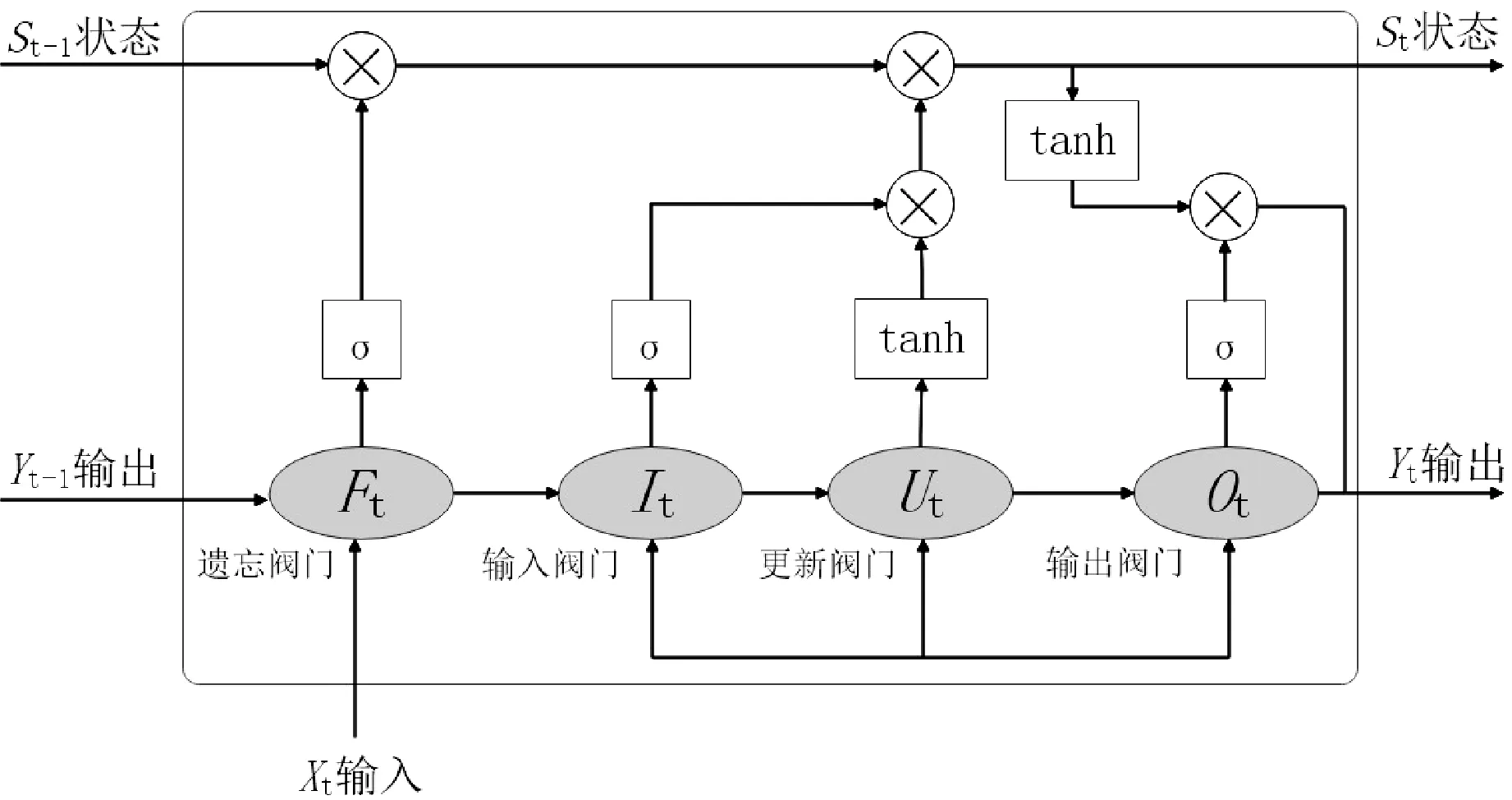
图2 LSTM基本网络架构

LSTM网络是由一个个的元细胞构成，组成相应的元细胞输送带，保证信息在整个链上保持不变，能够解决长时依赖的问题，学习到更远的规律。

遗忘阀门Ft通过Sigmoid激活函数获取旧元胞输出值Yt-1和当前元胞输入值Xt，结合相应的偏置和权重来判断是否应该保留当前元胞的状态St。计算公式：

Ft=σ(Wt[Yt-1,Xt]+bf)

(1)

式中：Wt是遗忘门对应的权重；Wt和bf分别是遗忘门的偏置和权重；σ是Sigmoid激活函数。

输入阀门It负责判断输入值Xt是否应该用于更新当前元胞的状态St，一方面由Sigmoid激活函数决定当前元胞输出值Yt，另一方面由tanh激活函数创建一个当前元胞的候选矢量Ut，由更新阀门判断是否应将其加入到当前元胞的状态St中。计算公式：

It=σ(Wi[Yt-1,Xt]+bi)

(2)

Ut=tanh(Wc[Yt-1,Xt]+bc)

(3)

式中：Wi是输入门对应的权重；Wc是细胞状态对应的权重；bi和bc是输入门和细胞状态的偏置；Ut是计算过程中的候选值向量。

更新阀门Ut通过将遗忘阀门和输入阀门相乘来判断当前元胞是否应该将旧元胞的状态由St-1更新到St。计算公式：

St=Ft×St-1+It×Ut

(4)

输出阀门负责计算当前元胞的输出值。计算公式：

Ot=σ(Wo[Yt-1,Xt]+bo)

(5)

Yt=Ot×tanh(St)

(6)

式中：Ot是t时刻LSTM单元的输出；Wo是输出门对应的权重；bo是输出门的偏置。

1.1.2 基于LSTM的高平峰模式识别

对交通高平峰状态进行有效辨识，对公交到站时间的预测具有重要意义。根据公交到站的时间曲线特性，结合控制图模式识别理论[11]，本文研究的六种典型公交到站时间模式如图3和表1所示。

图3 公交到站时间的六种基本模式

表1 六种控制图模式及其表达式

为了有效模拟公交到站时间曲线以及避免耗时的人工标注，本文通过蒙特卡洛法(Monte Carlo)对公交到站时间数据进行模拟，其形式为：

y(k)=u+re(k)+ds(k),k=1,2,...,M

(7)

式中：y(k)是第k个班次的公交到站时间；u是平峰状态下公交到站时间的均值；re(k)=r×σ是公交车辆行驶过程中偶然因素引起的随机误差，其分布为re(k)∈N(0,σ)，σ是公交到站时间的标准方差，r∈(-1,1)的随机数；ds(k)是第k个班次的公交车辆在行驶过程中由其他因素引起的干扰值；k0是趋势发生的初始位置，当k-k0<0时，v0=0，表示趋势状态未发生；当k-k0≥0时，v0=1，表示趋势状态已发生；kp是趋势模式的斜率，其中kp=kσ/10；k1是阶跃发生的初始位置，当k-k1<0时，v1=0，表示阶跃状态未发生；当k-k1≥0时，v1=1，表示阶跃状态已发生；sp是阶跃幅值，sp∈[2σ,3σ]；Ap是波动幅值，Ap∈[σ,1.5σ]；Tp是周期长度，Tp∈[5,8]。

本文每种模式产生Q个样本，每个样本选取M个连续的公交到站时间，构成LSTM模型样本集，进而对高平峰模式识别模型进行训练和测试，以ROC曲线(Receiver operating characteristic curve, ROC曲线)和AUC值(Area Under Curve，AUC)作为模型评价指标，最后对实际的公交到站时间数据进行识别。

1.2 基于LightGBM的到站时间预测模型

1.2.1 LightGBM工作原理

梯度提升树是经过多轮迭代来不断提高学习器的性能，在迭代过程中，假设前一轮得到的学习器是Ft-1(x)，损失函数是L(y,Ft-1(x))，那么本轮的目标就是找到一个弱学习器ht(x)，使得本轮的损失函数最小。损失函数为：

(8)

然后计算损失函数的负梯度，用于拟合本轮损失函数的近似值。损失函数的近似值可表示为：

(9)

最终得到本轮的强学习器：

Ft(xi)=ht(x)+Ft-1(x)

(10)

由于梯度提升树在处理大数据集时计算开销非常大，难以在精度和效率之间达到一个比较好的平衡，LightGBM算法对梯度提升树进行了改进，进而提升了模型的计算效率，并且在维持较高计算效率的同时还能得到较高的准确率。

1.2.2 基于LightGBM算法的到站时间预测模型

基于预处理后的数据进行模型训练和测试。以MAPE作为模型评价指标，模型的输出为到站时间，模型的输入包括高平峰模式、行车方向、前N个班次的到站时间、天气、时间特征、日期信息等。

时间特征提取：将一天中每h划分为4个区间，每个区间15min，即将一天24h划分为96个区间，对每个区间进行编号，则为1,2,3,…,96。如早上6：00，对应的区间刻度为24；早上7:20，对应的区间刻度为30；早上8:10，对应的区间刻度为33。

由于公交到站时间受节假日等因素影响，如果仅仅以是否节假日作为特征，模型会丢失节假日与非节假日之间的数据关联性。因此，本文从每条记录的日期信息中提取出5个特征作为模型输入，其中：第一个维度V1表示是否是节假日，取值范围0或1，如果是节假日，值为1，否则为0；第二个维度V2表示当天所在的日期类型(工作日或节假日)有多少天；第三个维度V3表示当前日期在工作日或节假日中所占的比例；第四个维度V4表示当天之前最近的连续不同的日期类型(工作日或节假日)天数；第五个维度V5表示当天之后最近的连续不同的日期类型(工作日或节假日)天数。以非节假日和国庆节为例，重构后的日期信息见表2和表3。

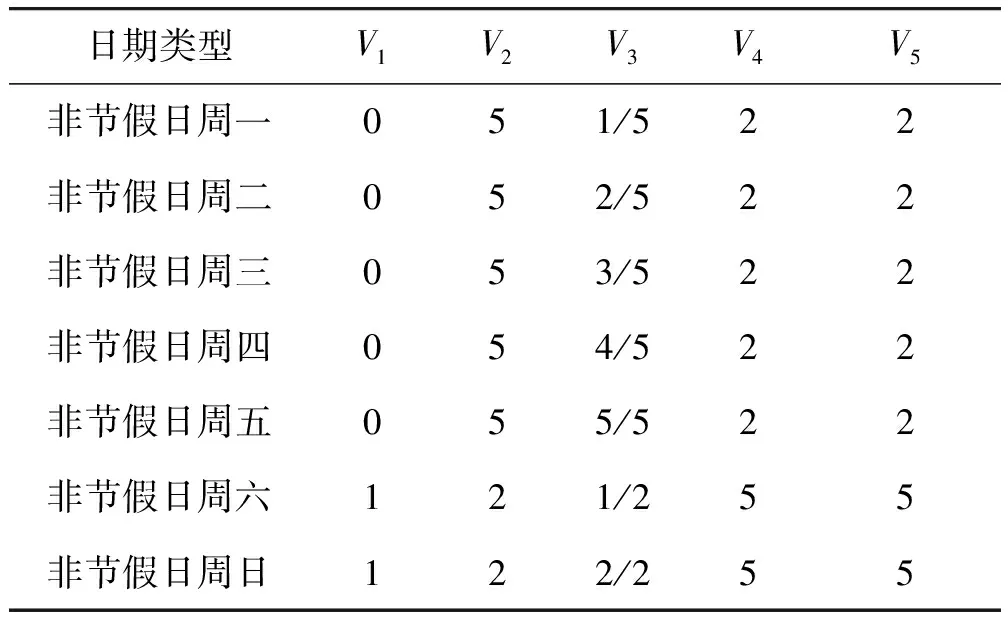
表2 非节假日的重构后的日期信息

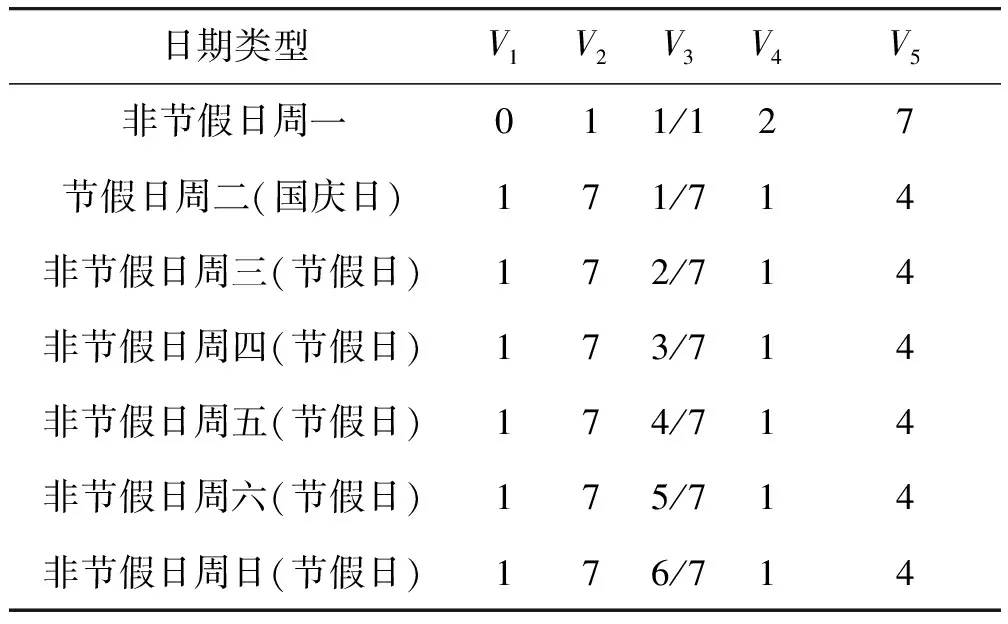
表3 国庆节期间的重构后的日期信息

2 实验与分析

2.1 原始数据描述

本文研究对象是广州市336路公交线路，从大观路北总站(大观湿地公园)至中海誉城总站。从公交调度系统中提取该线路的站点数据、电子路单数据、公交到离站数据、路网数据、公共汽(电)车畅行指数和天气数据等，采样时间从2019年10月1日至12月7日，得到基础数据集Xm×n(m表示样本量，n表示原始字段数目)，包括站台、日期、天气、道路、公交到达时间、离开时间等信息，其核心数据见表4。

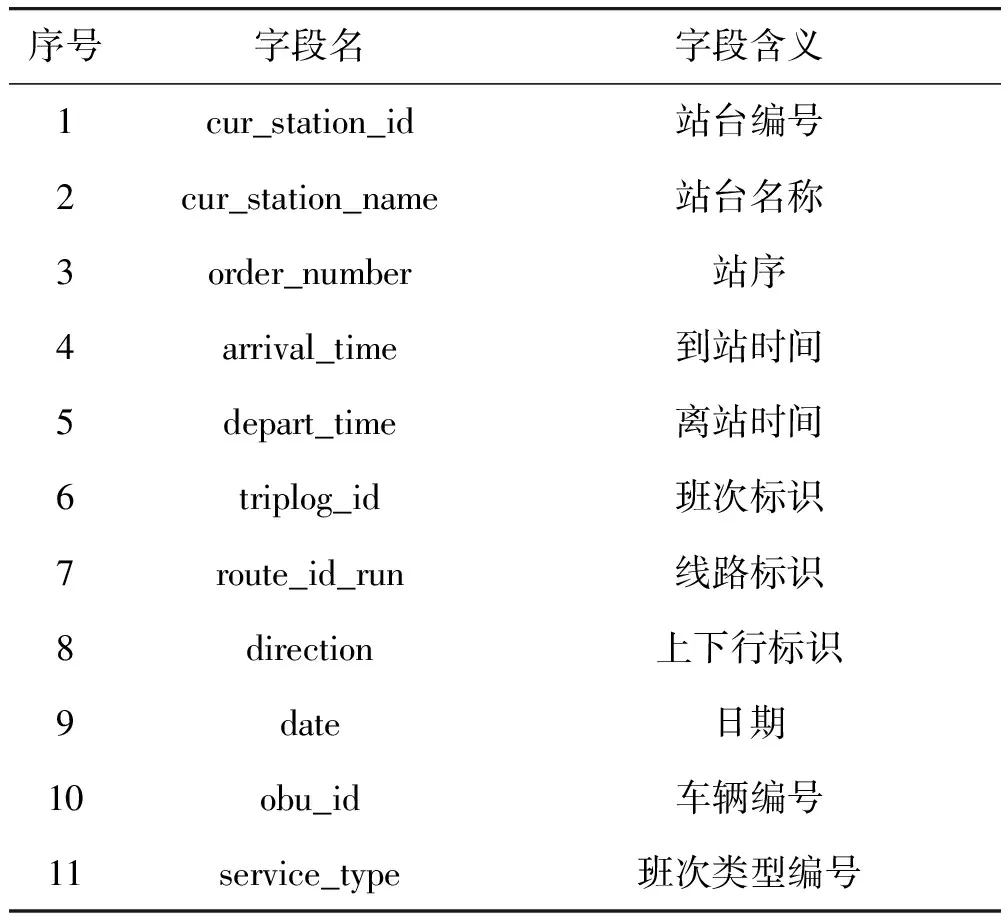
表4 公交核心数据信息

2.2 数据预处理

2.2.1 缺失值处理

缺失值处理主要有删除法和插补法。当缺失的信息占整个数据集的比例较低时，直接删除缺失值。如果到达时间arrival_time和离开时间depart_time两个字段的原始数据值出现缺失，本文采用均值插补法进行缺失值处理。

2.2.2 异常值处理

对于异常值的处理，是将数据集中与其他数据具有显著不同的孤立点、离群点等异常数据进行检测和删除。本文主要通过箱型图法剔除异常值。

2.3 数据特性分析

经过上述数据预处理，得到数据集Yk×n(k表示预处理后的样本量，k=197 504)。不同时间段的数据量占比情况见表5，数据整体分布相对均匀，早上7:00～9:59之间的数据量分别为7.75%、7.99%和7.50%；早上6:00～6:59之间的数据量最小，为2.17%。工作日与非工作日的数据量占比分别为51.47%和48.53%。

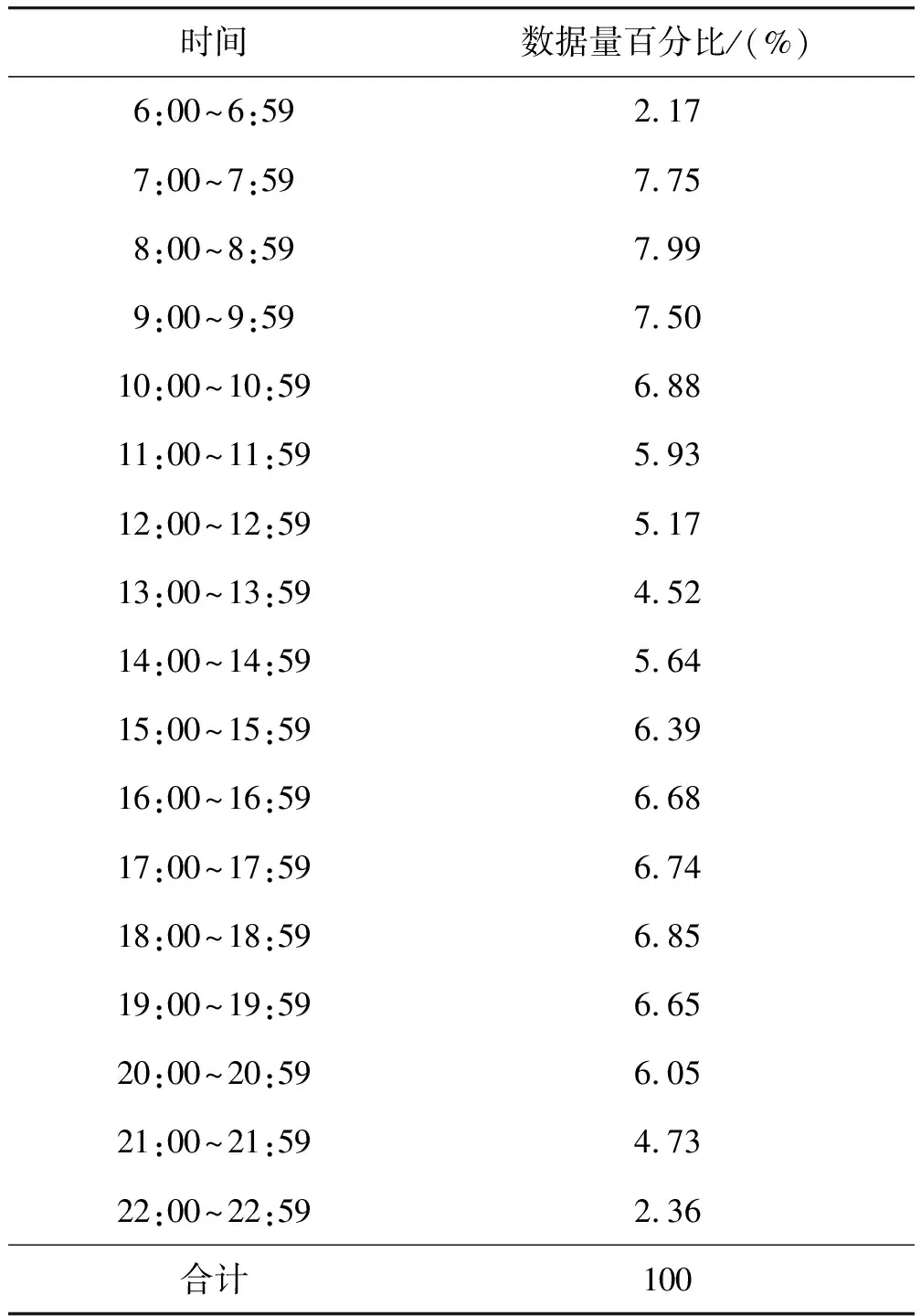
表5 不同时间段的数据量比例

图4表明单位站间的公交日均到站时间在一定范围内波动，其中站间编号为68561、680、6026、26963和26970的平均到站时间分别为163.34s、37.95s、74.92s、154.02s和77.73s。站间编号为68561和26963的路段为上下班高峰路段，站间距离较长、有1个红绿灯，工作日平均到站时间(166.78s和155.67s)要高于周末的平均到站时间(156.68s和149.78s)。站间编号为680、6026和26970的路段为非上下班高峰路段,其中680的站间距离短、没有红绿灯，公交到站时间短，在工作日(37.13s)和周末(38.37s)的平均到站时间非常接近；站间编号为6026和26970的路段站间距离较长、有1个红绿灯，公交到站时间适中，在工作日(74.58s和77.73s)和周末(75.64s和76.78s)的平均到站时间也非常接近。由图5可知，站间编号为68561和26963在11月18日不同时段的公交到站时间波动较大，早高峰的公交到站时间要高于平峰期和低峰期，晚高峰出现在17:00～18:00。

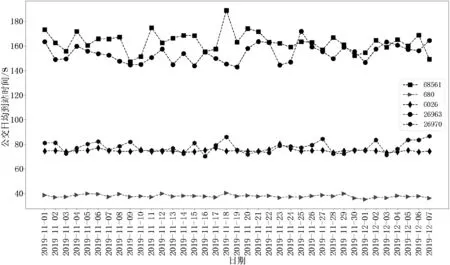
图4 不同单位站间的公交日均到站时间

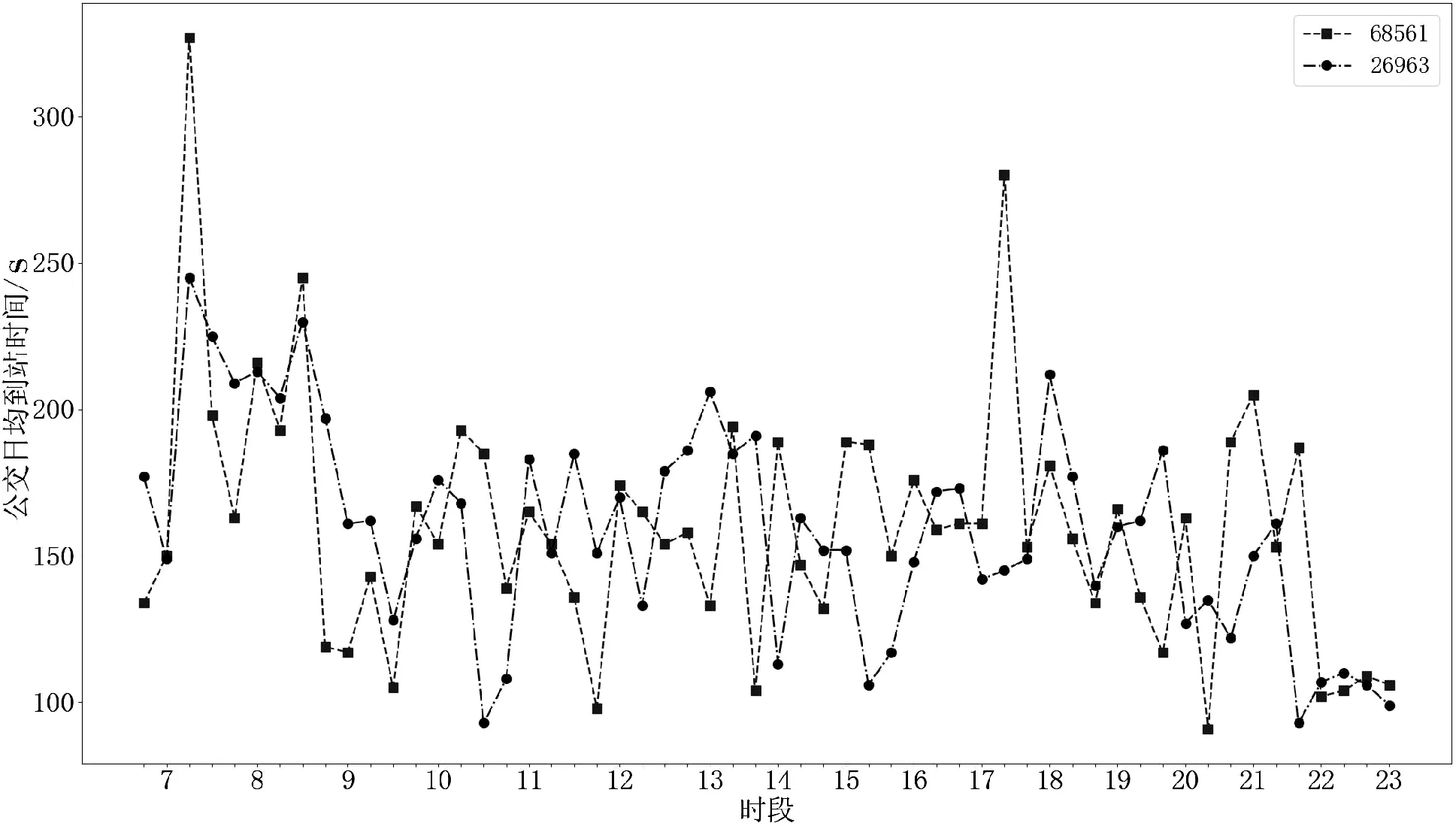
图5 站间编号为68561和26963在 11月18日不同时段的公交到站时间

图6和图7分别是公交车辆运行的单程时间密度分布曲线和累积分布曲线，单程时间集中在 3 000～4 000s，其中单程时间在3 000s内的概率为0.22，单程时间在4 000s内的概率为0.91。

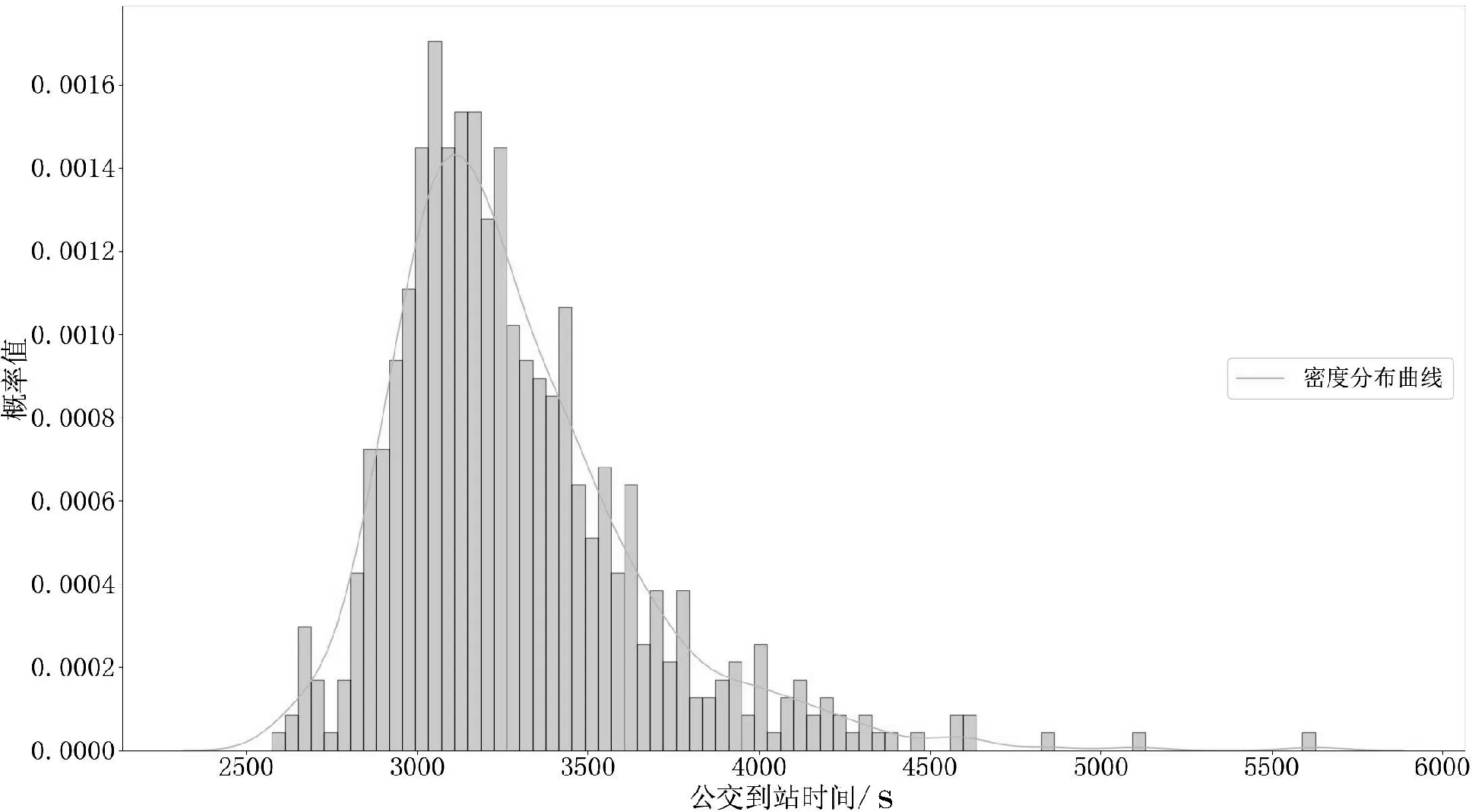
图6 公交车辆运行的单程时间密度分布曲线

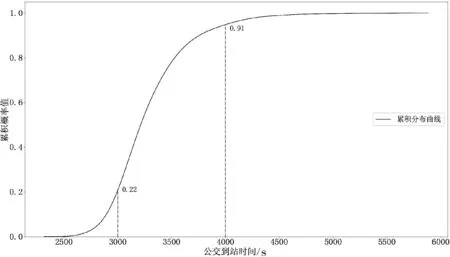
图7 公交车辆运行的单程时间累积分布曲线

2.4 模型结果分析

本文以2019年10月1日至2019年12月1日之间的2个月数据作为模型训练集，2019年12月1日至2019年12月7日之间的7d数据作为模型测试集。如1.1.2节所述，考虑到仿真数据的一般性，本文选取均值u=0，标准差σ=1，M=10，每种模式产生5 000个样本，每个样本选取10个连续的到站时间作为属性数据点，构成 30 000×10样本集，其中24 000×10样本是训练集，其余6 000×10样本是测试集。接收LSTM层输出全连接网络层(Dense层)的激活函数选择softmax函数；为避免模型训练过程中出现过拟合问题，丢弃部分隐藏层神经元网络节点的舍弃率为0.2。图8是不同的优化器对LSTM网络测试性能的对比情况，Adam算法的收敛速度最快，且性能表现最好；RMSProp算法性能表现次之；SGD算法的性能欠佳。因此，选择Adam算法作为LSTM网络的优化器。由图9可知，不同模型随参数变化时对高平峰模式的分类准确度，其中LSTM模型随着迭代次数的增加，分类精度处于99.12%，优于决策树和KNN分类模型，因此本文采用LSTM模型作为高平峰模式识别模型。

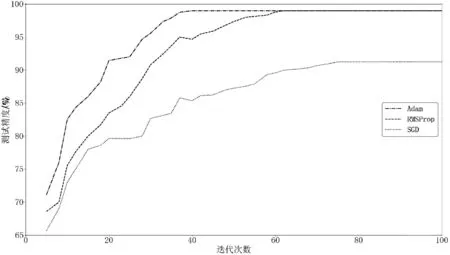
图8 不同优化器对LSTM网络性能的影响

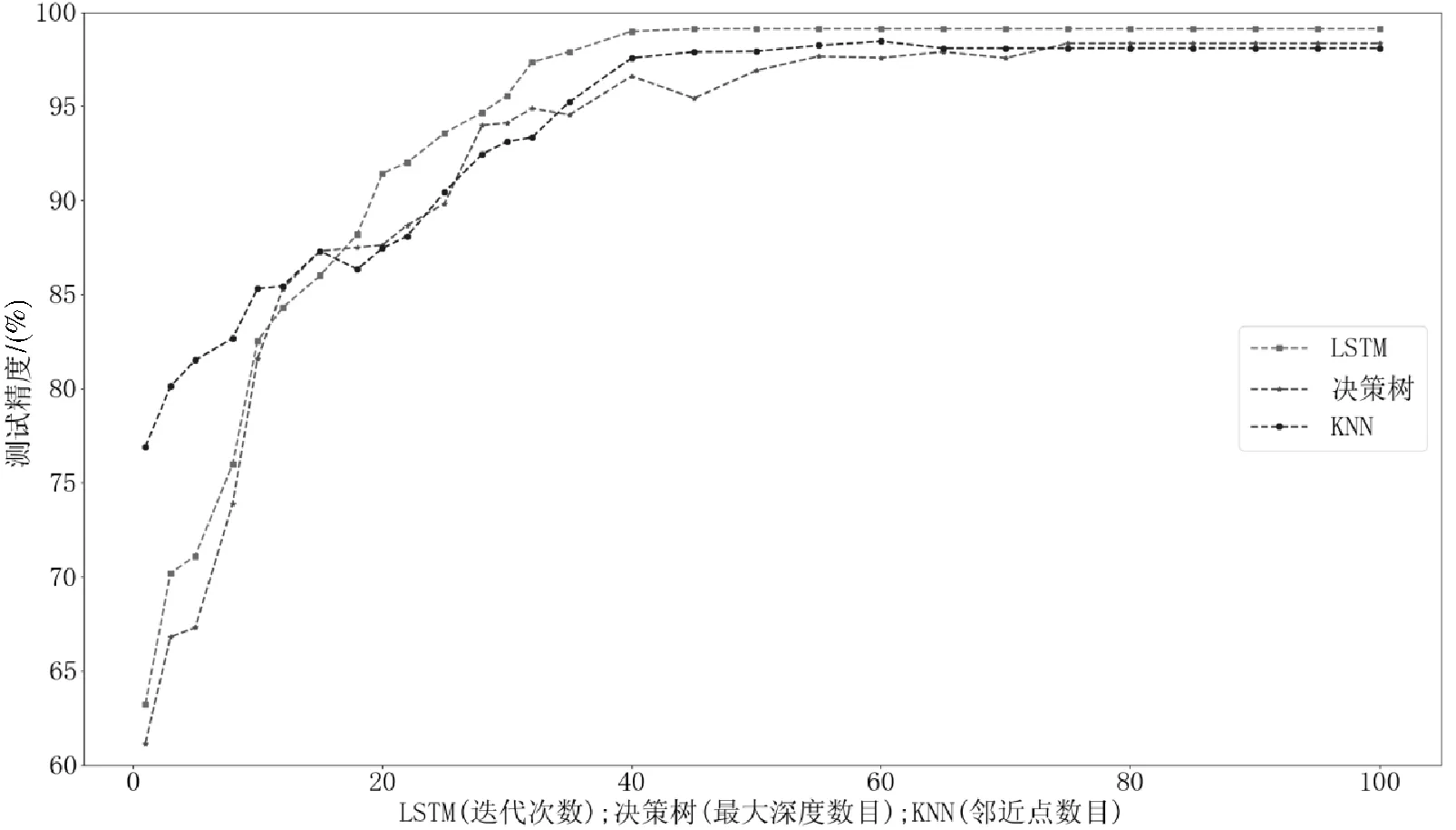
图9 不同模型对高平峰模式分类的 准确率随模型参数的变化

LightGBM模型的基本参数为：每棵树叶子的数量num_leaves和最大深度max_depth的取值范围是2～100；学习率learning_rate的取值范围是0.001～0.050；迭代次数的取值范围是50～10 000。从表6可知，各模型对非上下班高峰路段的预测精度要高于上下班高峰路段的预测精度。LightGBM模型的预测准确度要优于SVM模型、BP神经网络模型和多元线性回归模型，LightGBM模型在站间编号为680、6026和26970的MAPE低于9%，在站间编号为68561和26963的MAPE处于11.04%～14.07%。由图10可知，随着站序个数的增加，到站时间预测的精度会下降。

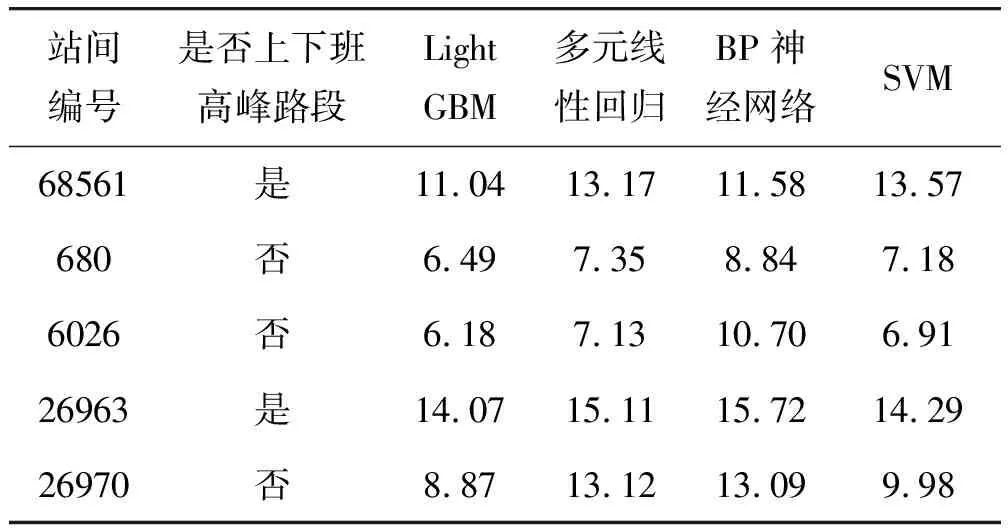
表6 预测结果误差对比，MAPE(单位：%)

图10 基于LightGBM模型的公交到站时间

3 结论

本文建立了一种基于LightGBM和LSTM算法的公交到站时间预测模型。首先通过LSTM算法构建高平峰模式识别模型对上下班高峰期状态进行有效辨识，然后以LightGBM算法进行到站时间预测。以广州市某典型公交线路为例，从公交调度系统中提取大量的历史数据进行预处理，分析了上下班高峰路段、时间刻度等对公交到站时间的影响，选择时间刻度、高平峰模式、上一个班次的到站时间、是否节假日等作为模型的输入，采用平均绝对百分比误差作为预测模型的评价指标。结果表明：基于LightGBM-LSTM模型的预测准确率要高于支持向量机模型、BP神经网络模型和多元线性回归模型。

影响公交到站时间的因素很多，如站间红绿灯数量、人行道数量、车流量、道路交叉口等，后续进一步的研究应将更多的影响因素考虑进来，结合更大规模的数据，对上下班高峰期的公交到站时间进行预测。