不同初始状态下压实黄土浸水后的变形特性研究

韩 哲, 高 游*, 熊勇林, 张俊然

不同初始状态下压实黄土浸水后的变形特性研究

韩 哲1, 高 游1*, 熊勇林1, 张俊然2

（1.宁波大学 土木与环境工程学院, 浙江 宁波 315211; 2.华北水利水电大学 河南省岩土力学与结构工程重点实验室, 河南 郑州 450045）

以压实黄土为研究对象, 通过一系列浸水后的压缩变形试验研究了不同初始含水率、初始干密度和竖向压力对非饱和压实黄土浸水后变形特性的影响. 结果表明: 非饱和压实黄土在相同竖向压力条件下, 浸水压缩稳定后的状态与初始状态无关; 压实黄土浸水后产生压缩变形的起始点压力值主要受试样初始干密度影响, 而终止点压力值主要受初始含水率影响. 其次, 根据不同初始状态非饱和压缩曲线的相互关系, 给出了考虑初始含水率和孔隙比影响的屈服应力计算方程. 最后, 基于非饱和压实黄土浸水前后的变形特性, 提出了定量化描述压实黄土浸水后压缩变形起始点和终止点压力值的计算模型.

非饱和土; 浸水; 变形特性; 压实黄土

近年来, 黄土在其分布地区常被作为建筑物或土工结构物等基础工程建设的填筑材料[1]. 在实际工程中, 建筑物或土工结构物等基础设施的破坏大多是由于降雨或地下水位线上升等浸水过程导致黄土地基在负荷状态下力学特性发生明显的变化, 从而产生过大的压缩变形[2]. 因此, 研究不同负荷状态下黄土浸水稳定后的变形特性, 对于黄土区域工程建设有重要的指导意义.

目前, 已有不少学者对黄土在增湿或浸水过程中的变形特性做了大量的研究. 相关研究指出, 以浸水后的沉降变形量来判定湿陷性黄土地区的场地优劣时常有过大差距[3]; 黄土的湿陷变形会随着加载增湿路径的不同而有所差别, 总变形包括压缩变形和增湿变形两部分, 增湿过程中随初始含水率的增大, 黄土湿陷系数呈递减的非线性关系[4-5]; 此外, 净围压和吸力等对屈服特性及湿化变形也存在较大的影响, 在净围压不变的情况下, 屈服应力和湿陷体变随着非饱和化程度的增加而增大, 在非饱和化程度不变时, 压缩指数和屈服应力皆随净围压的增大而增大[6-12]. 在微观机理方面, 研究人员结合微观孔隙结构系统地分析了黄土增湿过程和原状黄土与重塑黄土的压缩变形机理, 指出压缩变形量主要是集聚体间较大孔隙的压缩而产生[5,13].关于黄土浸水或增湿变形的宏微观机理的大量研究工作发现, 负载压力的大小是影响浸水或增湿过程中压实黄土是否产生湿化变形的重要因素.

在不同初始条件和压力状态下, 若能确定黄土在增湿或浸水过程中产生湿化变形的竖向压力值范围, 就可以判断某种状态下的黄土是否湿化. 但对不同初始状态的压实黄土在增湿或浸水过程中的变形特性、产生湿化变形的竖向压力值缺少系统分析. 因此, 本文首先基于不同初始状态的压实黄土浸水变形特性试验结果, 指出浸水稳定后的状态线与初始状态无关. 其次, 对不同初始状态下压实黄土浸水后产生压缩变形的起始点压力值和终止点压力值进行了分析, 提出了定量化描述压实黄土浸水后产生压缩变形的起始点和终止点压力值的计算方法. 最后, 结合相关实测数据进行了验证.

1 试验概况

1.1 试样制备

试验所用的黄土取自河南三门峡. 图1为黄土的颗粒级配曲线, 其粉粒(>75μm)成分约占82.6%, 黏粒(<75μm)成分约占12.4%. 黄土的比重为2.70, 液限为27.69%, 塑限为18.6%.

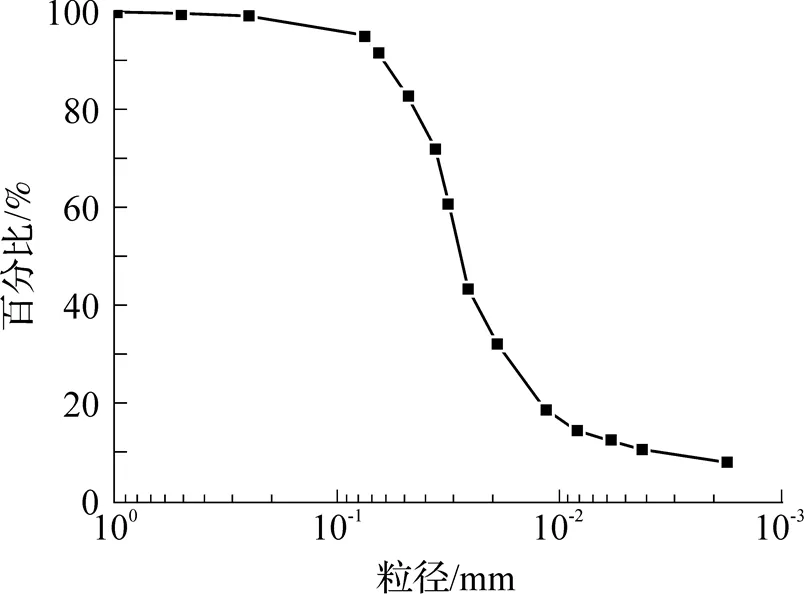
图1 黄土的颗粒级配曲线

本试验所有试样均采用静压的方法制备: 首先, 将土样风干、碾碎、过筛, 并根据初始含水率配制目标含水率; 其次, 将目标含水率的土样装入保鲜袋中静置24h, 以保证土样内部水分分布均匀; 最后, 根据目标含水率和干密度, 将定量的土样放入环刀压样模具中, 通过静态压实的方法一次性压样完成. 试样的直径和高度分别约为61.8和20mm. 将制备好的压实试样装入常规固结仪进行浸水变形特性试验.

1.2 试验方案

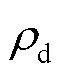
浸水变形特性试验的步骤如下: (1)将制备好的试样装入常规固结仪器, 先进行初步对中, 并安装百分表, 再施加预压力保证各部件接触良好; (2)读取百分表初值, 进行分级加载; (3)待试样竖向压缩稳定后, 对其进行浸水压缩试验, 稳定标准为试样2h的竖向变形量在±0.01mm范围以内. 试验过程中, 环境温度为(30±5)℃.

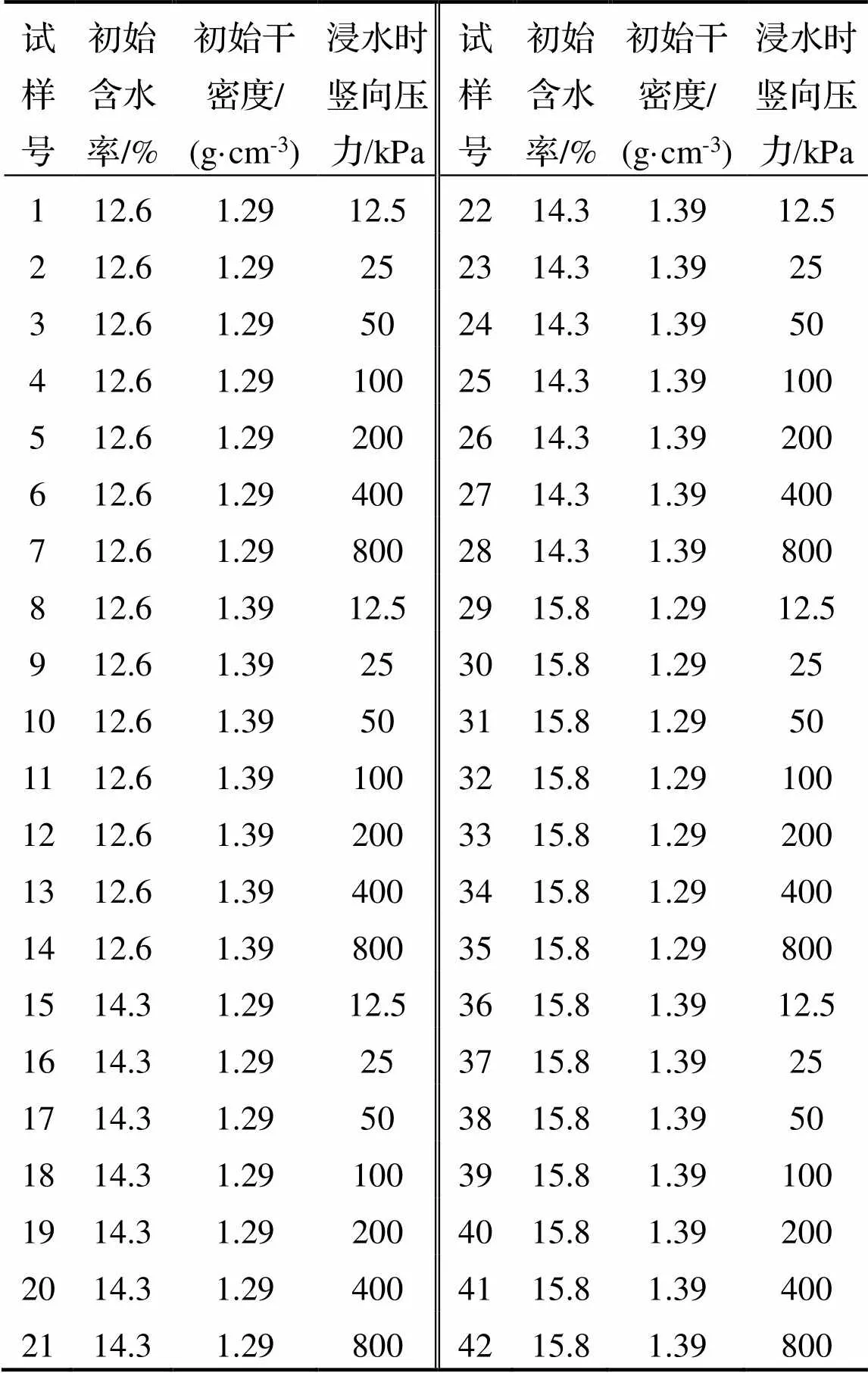
表1 试样的初始状态和浸水压力

2 试验结果分析

2.1 初始状态对浸水后变形特性的影响

图2表示黄土试样在不同初始状态和竖向压力条件下浸水前后的压缩变形曲线. 由图2可知, 在一定竖向压力范围内, 不同初始状态的试样浸水后均发生明显的压缩变形. 在初始含水率和竖向压力相同的条件下, 试样在浸水压缩稳定后的孔隙比()几乎一致. 其次, 任一初始状态的压实试样在不同竖向压力下浸水稳定后的状态线与非饱和压缩曲线均存在两个交点, 如图中和点, 分别称为变形起始点和终止点.和两点的物理意义为: 试样所承受的竖向压力值在起始点与终止点所对应的压力值之间, 在浸水后将产生明显的压缩变形; 反之, 试样在浸水后则不发生压缩变形. 此外, 对于不同初始状态的黄土试样, 其变形起始点的压力值随着初始干密度增大而增大, 变形终止点的压力值随着初始含水率的增大而减小.

图2 不同初始状态下压实黄土浸水前后的压缩变形曲线

综上分析可知, 压实黄土试样的初始干密度主要影响变形起始点压力值, 而变形终止点压力值主要受初始含水率影响.

图4表示原状黄土浸水前后的压缩变形曲线, 实测数据取自文献[14]. 由图可知, 在相同初始干密度和竖向压力条件下, 不同初始含水率的原状黄土试样在浸水压缩稳定后的孔隙比几乎一致. 其次, 任一初始状态的压实试样均存在一个变形起始点和变形终止点. 此外, 终止点压力值随着初始含水率的增加而减小, 而起始点压力值几乎不受影响. 本文实测数据与文献[14]原状黄土试样变形特性相近.

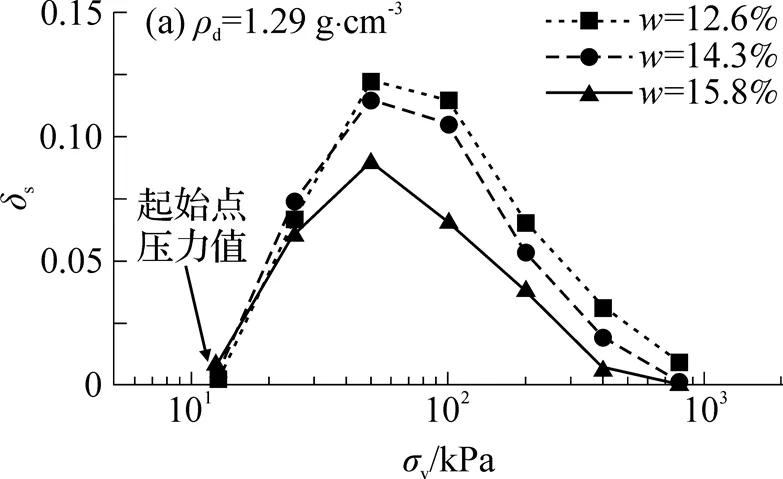
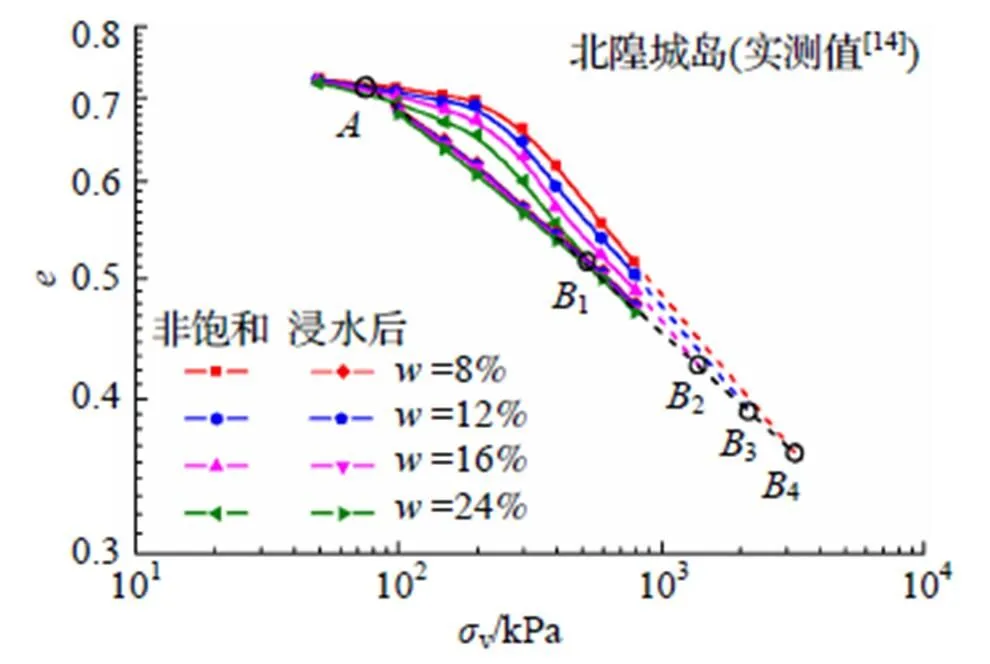
图4 原状黄土浸水前后的压缩变形曲线

2.2 初始状态对浸水稳定线的影响

图5为非饱和黄土试样浸水稳定后的孔隙比与竖向压力在双对数坐标下的关系曲线. 由图可知, 在双对数坐标中, 不同初始状态的压实黄土试样在不同竖向压力下浸水稳定后的孔隙比与竖向压力近乎为线性关系, 其拟合方差2为0.979. 即试样的初始状态对浸水压缩稳定后的状态线几乎无影响.

基于此, 压实黄土试样浸水后的稳定状态线在双对数坐标下可以表示为

式中: e为试样在浸水稳定后的孔隙比; sv为竖向压力, kPa; k和a为材料常数, 可以通过不同孔隙比浸水稳定点进行标定. 针对本文中的压实黄土试样,参数k和a分别取-0.166和0.195, 如图5所示.

若式(1)的稳定状态线已知, 任一初始状态下的非饱和压实黄土浸水稳定后而产生的压缩变形量可以由下式计算:

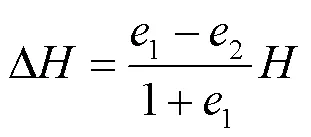
2.3 初始状态对非饱和压缩曲线的影响

图6为双对数坐标下不同初始状态的非饱和压实黄土试样的压缩曲线. 由图可知, 在初始干密度相同的条件下, 试样的屈服应力随着初始含水率的增大而减小, 结果与文献[7]类似. 同时, 相同初始含水率和不同初始干密度试样的压缩曲线在较大的竖向压力范围内接近重合.

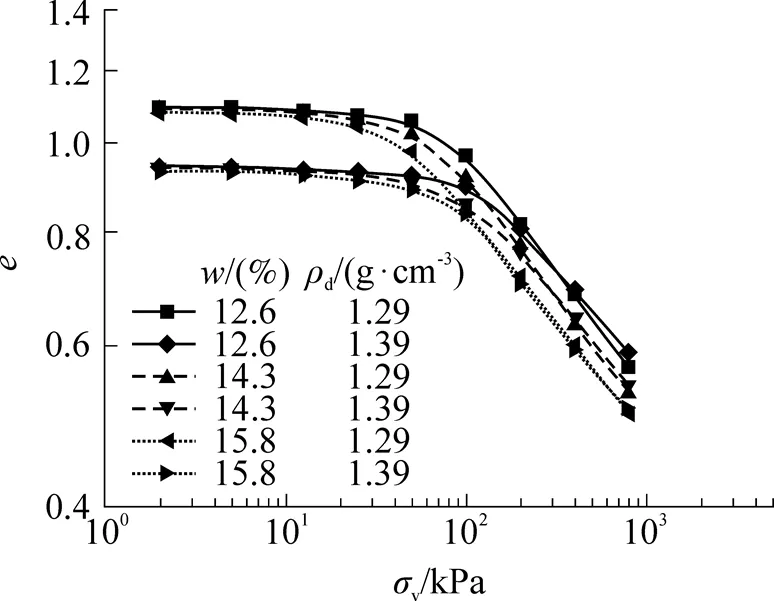
图6 非饱和压实黄土的压缩曲线

图7分别给出了在单对数坐标下压实黄土与原状黄土试样(实测数据来自文献[15])的初始含水率与屈服应力的关系曲线. 由图可以看出, 在单对数坐标下, 不同初始干密度的黄土试样其屈服应力与初始含水率几乎为线性关系. 因此, 不同初始状态试样其屈服应力与含水率的关系为

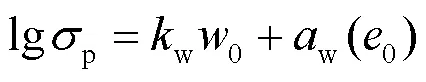
式中:p为屈服应力, kPa;w为斜率, 对于本文的压实黄土,w取-0.079;w(0)为初始孔隙比的相关函数. 若将w与0表示为线性关系, 则w(0)关系式可表示为

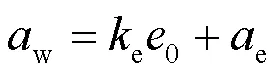
式中,e、e分别为斜率和截距, 可以由任意两不同初始孔隙比的屈服应力的两截距值进行标定. 对本文中的压实黄土, 参数e和e分别取值-1.69和4.71. 最后, 将式(4)代入式(3), 可得到考虑试样初始孔隙比和含水率对屈服应力影响的屈服应力方程:

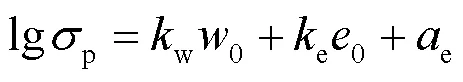
2.4 变形起始点与终止点的定量化描述

综上分析可知, 压实黄土的初始干密度主要影响浸水压缩变形的起始点, 而初始含水率主要影响变形终止点. 基于此, 在双对数坐标下不同初始状态的压实黄土在浸水前后孔隙比与竖向压力的关系曲线如图8所示, 图中e和c分别为非饱和压实黄土压缩曲线弹性段和弹塑性段的斜率.

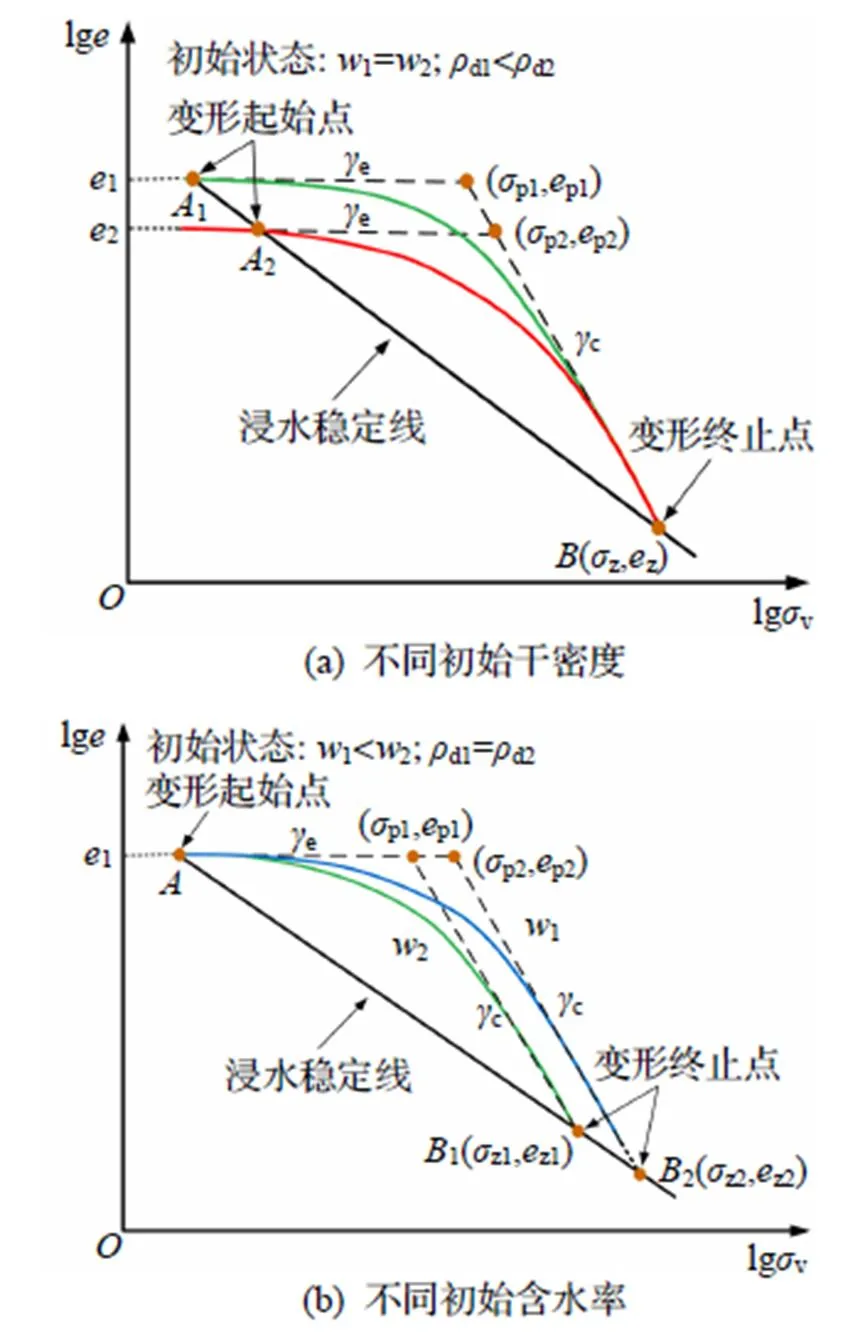
图8 黄土在不同初始状态下浸水前后的压缩变形曲线

若已知任意初始孔隙比(0)的压实试样在双对数坐标下的压缩曲线弹性段斜率e, 则压缩曲线弹性段的切线方程表示为

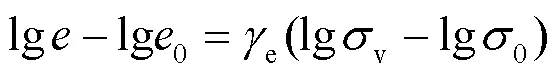
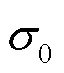
同理, 压缩曲线弹塑性段的切线方程表示为

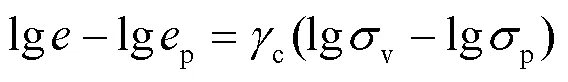
对于相同初始含水率条件下, 不同初始干密度的变形起始点坐标值(s,s)可以由式(1)与(6)联立求得:

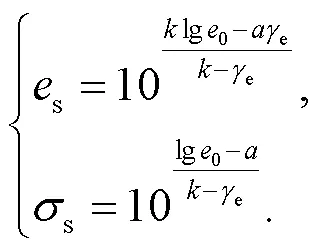
将孔隙比与干密度之间的关系0=s/d-1代入式(8), 即可得到与初始干密度相关的变形起始点压力值计算公式:

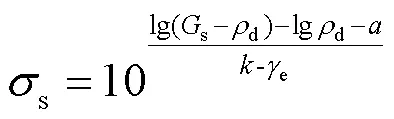
此外, 变形终止点的坐标值(z,z)可以由式(1)与(7)联立求得

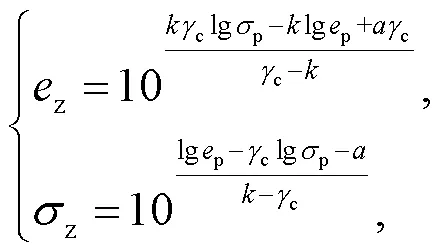
同时, 屈服点坐标(p,p)是压缩曲线弹性和弹塑性段两切线方程的交点, 可以将屈服点坐标值(p,p)代入式(6), 再联立式(5)和(10)即可得到变形终止点压力值的计算公式:

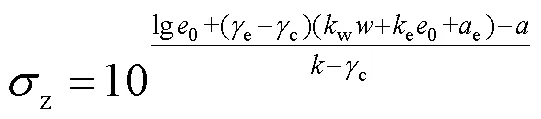
综上所述,若非饱和土在浸水后的稳定线方程已知,即可确定材料参数和;若非饱和土在双对数坐标下等含水率压缩曲线和屈服应力随初始含水率的变化曲线已知, 即可确定压缩曲线弹性段和弹塑性段的斜率e、c和屈服应力点参数w、e、e. 最后, 可利用已确定参数的式(8)和(11)对不同初始状态下非饱和压实黄土在浸水后变形起始点和终止点的压力值进行预测.

3 结论

(1)由浸水后的压缩变形试验可知, 非饱和压实黄土试样在相同竖向压力下, 浸水压缩稳定后的状态与初始含水率和干密度无关. 根据不同初始状态非饱和压缩曲线的相互关系, 提出了考虑初始含水率和孔隙比影响的屈服应力计算方程. 但该方程在广含水率范围内的适用性还需进一步验证.

(2)任一初始状态的非饱和压实黄土在不同竖向压力作用下均存在一个变形起始点和终止点. 基于试验结果分析可知, 变形起始点主要受试样初始干密度的影响, 而终止点主要受初始含水率的影响.

(3)基于非饱和黄土试样浸水前后的变形特性, 提出了一种定量化描述非饱和黄土变形起始点和终止点压力值的计算方法.

[1] 杨玉生, 李靖, 邢义川, 等. 压实黄土增湿变形性质及其影响因素试验研究[J]. 岩土工程学报, 2017, 39(4): 626-635.

[2] 孙建中, 刘健民. 黄土的未饱和湿陷、剩余湿陷和多次湿陷[J]. 岩土工程学报, 2000, 22(3):365-367.

[3] 谢定义. 试论我国黄土力学研究中的若干新趋向[J]. 岩土工程学报, 2001, 23(1):3-13.

[4] 周凤玺, 周志雄, 邵生俊. 非饱和黄土的增湿湿陷变形特性分析[J]. 岩土工程学报, 2021, 43(S1):36-40.

[5] Liu Z, Liu F, Ma F, et al. Collapsibility, composition, and microstructure of loess in China[J]. Canadian Geotechnical Journal, 2016, 53(4):673-686.

[6] 张登飞, 陈存礼, 于佃博. 非饱和原状黄土的变形及屈服特性试验研究[J]. 地下空间与工程学报, 2019, 15(2): 358-364.

[7] 陈存礼, 高鹏, 胡再强. 黄土的增湿变形特性及其与结构性的关系[J]. 岩石力学与工程学报, 2006, 25(7): 1352-1360.

[8] 陈存礼, 张登飞, 张洁, 等. 等向应力下原状黄土的压缩及增湿变形特性研究[J]. 岩石力学与工程学报, 2017, 36(7):1736-1747.

[9] Muñoz-Castelblanco J, Delage P, Pereira J M, et al. Some aspects of the compression and collapse behaviour of an unsaturated natural loess[J]. Géotechnique Letters, 2011, 1(2):17-22.

[10] Ng C W W, Cheng Q, Zhou C. Thermal effects on yielding and wetting-induced collapse of recompacted and intact loess[J]. Canadian Geotechnical Journal, 2018, 55(8):1095-1103.

[11] 张登飞, 陈存礼, 杨炯, 等. 侧限条件下增湿时湿陷性黄土的变形及持水特性[J]. 岩石力学与工程学报, 2016, 35(3):604-612.

[12] 方瑾瑾, 冯以鑫, 余永强, 等. 真三轴条件下的原状黄土增湿变形特性[J]. 岩土力学, 2020, 41(4):1235-1246.

[13] 韦雅之, 姚志华, 种小雷, 等. 非饱和Q3黄土微细观结构特征及对强度特性影响机制[J]. 岩土工程学报, 2021, 43(11):2127-2133.

[14] Zhang W, Sun Y, Chen W, et al. Collapsibility, composition, and microfabric of the coastal zone loess around the Bohai Sea, China[J]. Engineering Geology, 2019, 257:105142.

[15] 王丽琴, 邵生俊, 王帅, 等. 原状黄土的压缩曲线特性[J]. 岩土力学, 2019, 40(3):1076-1084; 1139.

Deformation behavior of compacted loess with different initial states after wetting

HAN Zhe1, GAO You1*, XIONG Yonglin1, ZHANG Junran2

( 1.School of Civil and Environmental Engineering, Ningbo University, Ningbo 315211, China; 2.Henan Province Key Laboratory of Rock and Soil Mechanics and Structural Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450045, China )

In this paper, a series of wetting tests on unsaturated compacted loess were performed to investigate the deformation behavior after wetting. The influences of different initial water contents, initial dry densities and vertical pressures were studied. The results indicate that under the same vertical pressure, the state of unsaturated compacted loess after wetting is independent of the initial states. The vertical pressure of the initial point after wetting is mainly affected by the initial dry density, while the vertical pressure of the termination point is mainly affected by the initial water content. According to the relationship of the unsaturated compression curves with different initial states, a yield stress equation considering the influence of initial water content and void ratio is proposed. Finally, based on the deformation behavior of unsaturated compacted loess before and after wetting, a simple method that can quantitatively describe the vertical pressure values of the initial point and the termination point is proposed.

unsaturated soil;wetting; deformation behavior; compacted loess

2021−10−17.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

浙江省自然科学基金（LY19E080012）; 河南省高等学校重点科研项目（21A410002）; 河南省高等学校青年骨干教师培养计划（2020GGJS-094）.

韩哲（1996－）, 男, 河南周口人, 在读硕士研究生, 主要研究方向: 非饱和土的水力特性. E-mail: hanzhe19960323@163.com

通信作者:高游（1989－）, 男, 浙江温州人, 副教授, 主要研究方向: 土力学. E-: gaoyou@nbu.edu.cn

TU411.5

A

1001-5132（2022）03-0019-06

（责任编辑 韩 超）