液体火箭发动机喷管仿真模型

孙得川，杨建文

(1.大连理工大学 航空航天学院，辽宁 大连 116024；2.西安航天动力研究所，陕西 西安 710100)

0 引言

化学火箭发动机使用拉瓦尔喷管作为能量转换的部件，用以产生推力，对其流场进行仿真分析是现代喷管优化设计和理解各种复杂流动过程必须经历的环节和步骤。随着计算流体力学(CFD)的发展，对喷管流动的仿真似乎已经不成问题，流行的CFD软件几乎都可以“轻松地”得到计算结果；但是得到结果容易，得到更接近真实值的结果却并非易事。尤其是现代喷管设计要结合具体的发动机条件，对性能仿真的准确性提出了更高的要求，以满足优化设计的目标。

喷管性能计算的发展历史主要以美国为代表。NASA早在20世纪60年代就开始研究发动机性能计算的程序，最初基于化学平衡假设，采用最小吉布斯自由能法来计算燃烧室和喷管的化学平衡状态，也可以计算透平机械、激波管等流动中的化学平衡问题。目前该程序的化学平衡部分代码已经基本公开，即近年来广为流传的CEA软件。在该程序的基础上，NASA主持开发了液体火箭发动机的二维化学动力学计算软件TDK(two-dimensional kinetics)并多次更新，可处理诸如三组元发动机、超燃冲压发动机中的化学反应流动问题。TDK软件预测的比冲与试车相比偏差在3%以内，已经成为美国JANNAF的标准软件，并且共享给其盟友使用，在液体发动机研制中发挥了重要的作用。

在众多文献中，Manski等对液体火箭发动机性能的研究比较具有代表性，他们利用TDK详细计算研究了SSME和Vulcain发动机的性能，重点讨论了室压对喷管效率的影响。其研究指出：对于氢氧一级发动机，当室压较低时喷管效率约为97%，而当室压提高到10 MPa时喷管效率可达98%以上；由喷管二维效应引起的扩张损失是总损失的主要部分，随着室压提高，扩张损失从初始的0.6%上升到1.5%；SSME的室压超过10 MPa后，化学动力学损失几乎为零，但是在低压情况下，化学动力学损失可达1%。可见，室压提高时喷管效率提高的主要贡献在于化学动力学损失减少。

与西方国家相比，国内在喷管性能的研究方面还比较欠缺，这主要是因为该研究内容偏于“老旧”，似乎缺乏创新。因此对于喷管流动和各种损失的理解还较为浅薄，这不利于建立在仿真基础上的发动机优化设计。

仿真是通过数学方法模拟真实世界，其“保真”有两个环节，首先是数学模型是否真正反映了物理过程，其次是求解数学模型的过程是否准确。笔者认为目前计算技术的发展已经可以保证第二个环节正确，喷管性能仿真准确度的提高主要取决于所采用的数学模型是否恰当。因此，本文以典型的液体火箭发动机喷管为例讨论气体模型、化学反应模型等对计算结果的影响，并进一步厘清影响喷管性能的物理因素，以期对发动机设计有所启发和帮助。

1 喷管性能的仿真模型

1.1 理想喷管

喷管性能以理想喷管的性能作为参照。理想喷管是出口压力等于环境压力的一维喷管，能够产生设计条件下的最大推力，其推力系数表示为

(1)

式(1)完全是根据气体等熵膨胀假设得出，可见理想推力系数仅与燃气的比热比和压比/相关。图1以压比为变量，给出了不同比热比所对应的曲线。显然，压比增大会得到较大的推力系数，即(在不发生流动分离的情况下)面积比大的喷管推力系数大。而在同样的压比条件下，如果燃气比热比较小，也可以获得较大的推力系数。

图1 理想喷管的推力系数与压比的关系Fig.1 Relationship between thrust coefficient and pressure ratio forideal nozzle

因为燃气的比热比与推进剂相关，并随化学反应流动而变化(燃气在喷管中流动时，由于温度下降和化学组分变化，比热比也随之变化，一般随面积比或压比增大而增大)，所以工程应用中一般以化学平衡流动所得到的比热比作为理想值。图2是采用一维化学平衡计算得到的某空间发动机喷管中燃气的比热比随面积比的变化。

图2 假设流动处于不同状态下，喷管中燃气比热比和主要组分与面积比的关系Fig.2 Relationship of specific heat ratio and main components to area ratio under different flow conditions

该发动机采用四氧化二氮/一甲基肼作为推进剂，混合比为1.65，室压为0.85 MPa。可以看到若假设燃气处于化学平衡状态，则比热比介于1.24～1.26之间；而若假定燃气冻结，则由于燃气组分不再变化，其比热比随燃气膨胀、降温而增大得较多；若考虑多组分处于化学非平衡，则得到的比热比略低于冻结流假设计算值。对照主要组分的变化，可见在化学平衡计算中，H和CO逐渐增多而CO和HO逐渐减少，但是在实际的反应流中，组分只在膨胀初期(面积比小于10)有明显变化，而后基本冻结。所以，喷管扩张段中的燃气更接近冻结流，其比热比大于平衡流的值。而由图1可知较大的比热比所对应的推力系数较小，故而不容易提高喷管的性能。

1.2 气体模型

由以上分析可知，比热比对准确预示喷管性能起决定性作用，而比热比的计算首先由所采用的气体模型决定。表1对比了喷管流场仿真中所使用的气体模型的特点。

表1 不同气体模型的特点Tab.1 Characteristics of different gas models

各模型的状态方程为

=

(2)

式中为气体常数，且=-。可见对于量热完全气体假设，其定压比热和比热比均为常数，而比热或比热比的确定则完全靠经验；对于喷管流动计算，常采用喉部位置的化学平衡计算值。

对于热完全混合气体假设，其中各组分的摩尔定压比热的计算常采用由JANNAF表拟合的多项式，即

(3)

式中：为通用气体常数；为组分序号。混合气的摩尔定压比热为

(4)

式中：为组分数量；为组分的摩尔分数。因绝大多数气体单质的定压比热都是随温度升高而增大的，所以混合气体的比热也具有同样的特点。

若假设气体组分冻结，则燃气成分的含量不变，故定压比热只与温度有关，一般随温度降低而减小。若假设气体组分处于化学平衡状态，则组分种类和含量都随温度瞬态变化、而与反应过程无关，通常用吉布斯自由能最小的方法求解组分及其含量。在真实的喷管流动中，燃气组分处于化学非平衡状态，必须采用化学动力学的方法求解。

1.3 二维非平衡流动的控制方程

二维非平衡流动的控制方程为轴对称N-S方程，各组分的质量守恒方程为

(5)

式中：为组分的净生成率；坐标和都以喉部半径进行无量纲化处理。对所有组分求和，得到混合燃气的连续方程为

(6)

动量方程为

(7)

能量方程为

(8)

其中

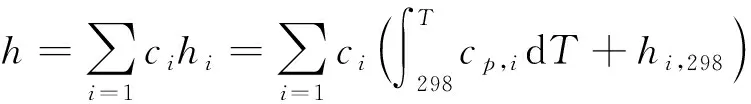
(9)

1.4 化学动力学模型

设混合气体中含有种组分，描述化学反应过程的机理含有个反应，反应机理表达为

(10)

式中:为反应序号;表示组分名称；和′分别为各组分在反应前、后的计量系数。

组分的净生成率为

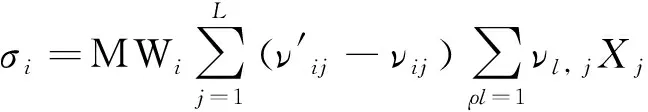
(11)

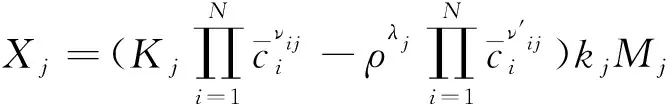
(12)

(13)

式中:为指前因子;为温度系数;a为活化能由反应机理给出。

1.5 湍流模型

对于没有流动分离的喷管流动，湍流模型对计算结果的影响很小。本文采用经典的-两方程模型，近壁处采用壁面函数法处理，在此不赘述。

1.6 控制方程求解

因喷管结构相对简单，可采用结构网格，故在计算程序中对空间差分采用了适用于结构网格的三阶WENO格式，对时间推进采用三阶精度的Runge-Kutta格式。

对于化学反应源项，有

(14)

当只考虑反应引起的质量变化时，有

(15)

其中

(16)

采用如下半隐式梯形公式求解

(17)

边界条件按照如下方法给出：入口边界指定流量，其温度和化学成分组成由化学平衡计算确定；壁面边界为无滑移条件，压强、温度、组分浓度梯度为零；轴线边界只有轴向速度，压强、温度、组分浓度梯度为零；出口边界为无反射条件。

2 典型喷管的性能仿真分析

2.1 喷管参数及计算条件

本文针对3个发动机喷管进行了仿真研究，其参数见表2，其中针对喷管Ⅱ还计算了室压为22.0 MPa的情况，以评估室压对化学动力学的影响。

表2 喷管参数Tab.2 Nozzle parameters

图3给出了喷管Ⅰ的计算网格，其轴向节点数为151，径向节点数为51，在喉部和壁面附近加密。其中壁面第一层网格的≈30～50，与湍流模型适应，不影响摩擦损失的计算。其他两喷管的网格类似。

图3 喷管Ⅰ的计算网格Fig.3 Calculation grid of nozzle Ⅰ

喷管入口温度、组分及其含量由化学平衡计算给出，见表3。采用的反应机理见表4和表5。

表3 喷管入口温度、组分及质量分数Tab.3 Temperature， component and mass fraction at nozzle inlet

表4 CHON系统的反应速率Tab.4 Reaction rate of CHON system 单位:cc，K，mole，sec

表5 CHON反应的三体系数Tab.5 Coefficients of the third body for CHON reaction

2.2 气体模型的影响

首先针对喷管Ⅰ用不同气体模型进行性能计算。采用量热完全气体假设时，燃气的比热值设为2 156.6 J/(kg·K)(该值为燃烧室化学平衡计算结果，对应比热比为1.232 7)，对应的温度为3 042 K。图4对比了按不同气体模型所计算的喷管温度场。

图4 喷管Ⅰ内的温度分布Fig.4 Temperature distribution in nozzle Ⅰ

可以看到采用量热完全气体假设所计算的喷管出口最低温度约为500 K，而采用冻结的热完全气体假设所计算的出口温度则明显偏低，非平衡气体的出口温度则介于两者之间。另外在紧靠喷管喉部的初始膨胀段，采用量热完全气体假设和热完全气体假设计算得到的温度等值线接近，呈更加外凸的形式，而化学非平衡计算的等值线曲率则较小。相应地，因采用量热完全气体计算的喷管出口温度较高，所以对应的马赫数较低(见图5)。

图5 喷管Ⅰ内的马赫数分布Fig.5 Mach number in nozzle Ⅰ

3种气体模型所计算的轴向速度分布见图6，其中冻结的热完全气体所对应的出口速度明显低于其他两种情况。另外，从温度和马赫数分布可以观察到当采用量热完全气体和冻结的完全气体假设时，喷管内从扩张段起始的压缩波较明显，等值线的折转较突然；而实际的非平衡气体流动中，等值线折转比较圆滑，说明组分的变化起耗散作用，而且这种影响起源于扩张段的起始部分。

图6 喷管Ⅰ内的轴向速度分布Fig.6 Axial velocity distribution in nozzle Ⅰ

图7显示了反应中自由基团OH的分布，因OH是反应中的活性组分，其浓度可以反映出反应的活跃程度，所以该图表示喉部附近的流动为非平衡流动，在面积比较大的喷管下游才能视为冻结流动。

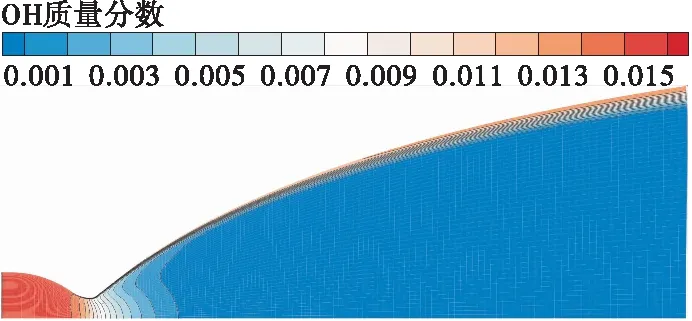
图7 喷管Ⅰ内OH组分的质量分数Fig.7 Mass fraction of OH in nozzle Ⅰ

表6列出了采用不同气体模型计算的喷管Ⅰ的真空比冲与理论值和试车测量值的对比。比较可知，二维化学动力学计算得到的真空比冲与发动机实测值最接近，除燃烧效率之外的综合效率为94%；若考虑实际燃烧效率大于98%，则采用化学动力学计算的发动机比冲将落在试车值范围内，这充分说明了化学动力学计算的准确性；而采用量热完全气体和热完全气体假设所计算的效率都偏高。

表6 计算得到的喷管Ⅰ的性能Tab.6 Calculation performance of nozzle Ⅰ

为了更进一步说明气体模型对计算结果带来的影响，表7给出了采用不同模型计算的喷管Ⅱ的比冲。

比较表6和表7可知，采用量热完全气体假设所计算的比冲高于用热完全气体假设的计算值。这是因为量热完全气体假设比热比不变，而热完全气体的比热比随温度降低而增大，这符合式(1)(图1)对于比热比对喷管性能影响的说明。但是在喷管Ⅰ的计算中，采用量热完全气体或热完全气体假设所计算的比冲比二维化学动力学计算的比冲高，而在喷管Ⅱ的计算中恰恰相反。造成这种差异的原因可能有二，其一是两种发动机所采用的推进剂组合不同；其二正是化学动力学损失的影响，喷管Ⅰ的室压较低，化学动力学损失较大，而喷管Ⅱ的室压较高，化学动力学损失较小。

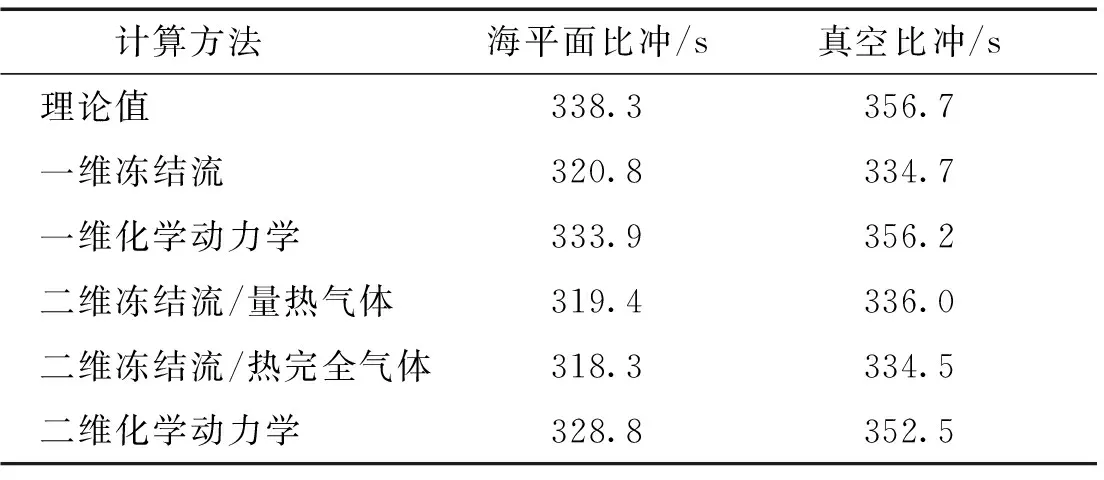
表7 计算得到的喷管Ⅱ(pc=17.7 MPa)的性能Tab.7 Calculation performance of nozzle Ⅱ(pc=17.7 MPa)

目前喷管性能的CFD计算中，很多都采用量热完全气体或热完全气体假设，这显然会造成较大的偏差。

2.3 室压对化学动力学的影响

理论上讲，提高燃烧室压强有助于提高发动机性能。这主要有两方面的原因：其一是提高室压会提高燃烧效率，其二是高室压下喷管的化学动力学损失小。

为了说明第二点，对比了喷管Ⅱ在17.7 MPa和22.0 MPa室压下的化学非平衡流场。计算时给定两个算例的入口组分含量完全相同，相当于燃烧效率相同。计算得到当室压提高到22.0 MPa时，比冲为329.8 s，比表7给出的室压为17.7 MPa时的比冲328.8 s高了1.0 s。

为了解室压增大提高喷管性能的原因，图8对比了用两种室压条件计算的喷管Ⅱ的流场参数。由该图可知，从马赫数是很难分辨出差别的。但是静温的等值线分布说明了高室压下性能略高的原因，高室压下具有相同值的等值线略偏向下游，这说明在喷管相同位置，高室压所对应的静温略高，即混合燃气的能量更高。提高室压可以略提高燃气温度的原因在于碳氢燃料燃烧中的重要基元反应，即CO+O=CO，该反应是主要的放热步骤。因为该反应是聚合反应，反应物的分子数多于产物的分子数，所以增大室压使该反应向偏向于生成CO的方向移动，即放热量增大。图8(c)和图8(d)中CO和CO质量分数的分布证明了这一点，即提高室压使CO消耗得更快一些而CO生成得更多一些。

图8 不同室压条件下喷管Ⅱ内参数对比Fig.8 Comparison of internal parameters of nozzle Ⅱ under different chamber pressures

2.4 喷管型面对性能的影响

喷管Ⅱ和喷管Ⅲ所对应的发动机均采用了液氧/煤油推进剂，混合比也都是2.62，但是室压不同、特征尺寸也不同，喷管内型面曲线均采用Rao方法设计。为了比较两个喷管性能的差异，将两个喷管都用喉部尺寸进行无量纲化处理，使喉部之前的无量纲型面重合。图9显示喷管Ⅱ、Ⅲ的无量纲型面曲线非常接近，在面积比较小时基本重合。

图9给出了两个喷管内的静温等值线，与图8(b)基本一致，这说明喷管Ⅲ在提高室压后燃气具有较高的能量，对应更高的性能。

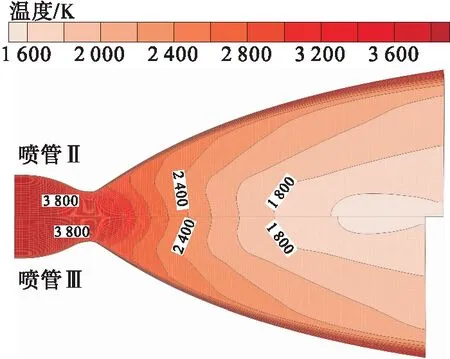
图9 喷管内温度场(喷管尺寸无量纲处理)Fig.9 Temperature field in nozzle (dimensionless treatment for nozzle size)

图10给出了两个喷管在面积比分别为4、9、16、25、32各截面的比冲。为了讨论室压的影响，图中还给出了喷管Ⅱ在室压为22.0 MPa条件下的比冲。对于喷管Ⅱ，当室压提高到22.0 MPa后，各截面的比冲都提高了1.0 s左右，但是仍然比喷管Ⅲ对应(面积比相同)截面的比冲低。

从图10看到，两个喷管的型面在面积比小于4之前基本完全相同，但是计算得到比冲相差0.9 s；在面积比较大的位置，喷管Ⅲ的比冲约高1.0 s左右。产生这种差异的原因在于，针对喷管Ⅱ计算室压22.0 MPa条件时只是增大了入口流量，其他入口参数(组分和总温)与17.7 MPa工况相同，而喷管Ⅲ的入口则用的是22.0 MPa的化学平衡计算结果，这相当于喷管Ⅲ的燃烧效率略高。考虑到这个因素，在相同入口条件下，两个喷管在相同面积比下的比冲基本相同。这也说明，喷管Ⅲ的型面实际是偏瘦的，即在相同性能要求下采用喷管Ⅱ的型面可以略短；换个角度说，这是因为喷管设计采用了Rao方法而没有考虑黏性效应，进行附面层修正后应可以略提高性能。

图10 喷管各截面的比冲(虚线上方的值对应17.7 MPa，下方的值对应22.0 MPa)Fig.10 Specific impulse of each section of nozzle (the values above the dashed line corresponds to 17.7 MPa and the values below corresponds to 22.0 MPa)

3 结论

本文对液体火箭发动机喷管仿真的计算模型进行了详细的分析，并通过3个喷管、4种工况的仿真详细讨论了气体模型对仿真结果的影响，以及室压、喷管扩张段型面对性能的影响。根据分析，本文得到如下主要结论：

1)采用量热完全气体假设所计算的比冲高于用热完全气体假设的计算值；这两种气体模型给出的计算结果偏差较大，可能高于、也可能低于二维化学动力学计算结果，没有规律性；二维化学动力学计算结果比较准确，接近试车测试值。

2)提高室压不仅能提高燃烧效率，也能促进聚合反应、减小流动过程中的化学动力学损失，使喷管性能提高。

3)Rao方法设计的喷管型面偏“瘦”，进行附面层修正可略提高性能，或在同样性能要求下略减小喷管长度。