一种基于串联输入并联输出型LLC的噪声抑制磁集成方法

王议锋 陈 晨 陈 博 朱洪卿 张明智

（1. 天津大学智能电网教育部重点实验室 天津 300072 2. 国网东营供电公司 东营 257091）

0 引言

提高功率半导体器件的工作频率是提高电能变换器功率密度的有效途径，但是传统PWM变换器具有较大的开关损耗，影响了变换器的变换效率[1]。为了兼顾功率密度和工作效率，软开关变换器应运而生[2]。在众多软开关型拓扑中，谐振型软开关变换器以其简单的拓扑结构和易于实现的软开关特性，引起了研究人员的广泛关注。与两元件谐振变换器相比，LLC变换器具有良好的调压特性和软开关特性，因此被广泛应用于各类高频降压变换场合[3-4]。

随着高频磁性材料和平面磁技术的飞速发展，平面变压器已经成为中低功率电能变换器设计的首选[5]。基于磁通抵消原理，文献[6-7]提出了矩阵变换器的概念，显著降低了磁心的磁通密度，其绕组“一次侧串联，二次侧并联”的连接方式大幅降低了二次侧开关器件的电流应力。然而平面变压器采用印制电路板（Printed Circuit Board, PCB）绕组，绕组间的寄生电容更大[8]。

由于高频下平面变压器的寄生参数愈发明显， 而LLC变换器又对谐振腔中各元件寄生参数的作用比较敏感，因此高频平面变压器的使用影响了LLC变换器的调压性能[9]。此外，变换器工作频率的大幅提升引入了较大的电压、电流变化率。较大的dv/dt、di/dt沿着有源线路和变压器的杂散参数进行传导，产生的共模（Common Mode, CM）噪声不容忽视,导致变换器出现较为严重的电磁干扰（Electromagnetic Interference, EMI）问题[10]。

目前针对平面变压器的EMI问题的解决方案大致分为屏蔽法、噪声源抑制法和抵消法三类。文献[11]通过在平面变压器的一次、二次绕组之间嵌入与二次绕组完全相同的屏蔽层，有效地阻碍了噪声的传导；文献[12]基于文献[6]提出的矩阵变压器结构改进了平面变压器的噪声屏蔽方法：通过将部分屏蔽层与一次侧串联，构造出17:1:1的匝比，证明了噪声屏蔽效果不受屏蔽层角度的影响，大幅降低了屏蔽层带来的端接损耗，在实现噪声抑制的同时保证了拓扑的高效率变换；文献[13-14]运用了“成对层”（paired layer）的思想，分别对反激变换器和LLC谐振变换器进行了噪声屏蔽处理，目的在于在相邻的一次、二次绕组端口构造出相同的dv/dt，不需额外引入元件，但是此类方法仅适用于每层单匝绕组的平面变压器，限制了绕组结构的设计。文献[15]提出了一种变压器的串联输入并联输出（Inputs Serious and Outputs Parallel, ISOP）结构以构造多组噪声静态点，使得共模噪声的幅值仅为初始的1/8，继而通过合理控制开关的相位抵消各胞元磁心内部和外部的共模噪声，达到了显著的噪声抑制效果，但是考虑到驱动多组半桥逆变结构开关管对辅助电源要求较高，难以应用于实际工程。

本文在文献[15]所提拓扑的基础上进行了深入研究。首先对拓扑的噪声源、噪声传导路径进行了详细分析，并预测了共模噪声，推导相应的数学公式，总结了变换器噪声的影响因素，解释了拓扑的噪声抵消控制原理；其次，采用磁集成技术，重新设计了拓扑的磁件，并提出了一种二次绕组的优化设计方法；然后，为了验证所提方法的有效性，采用电磁仿真软件Maxwell搭建3D模型进行仿真，验证理论的可行性与正确性；最后搭建了一台额定功率500W的实验样机，实现了较高的变换效率。

1 拓扑的工作原理

采用屏蔽法虽然能改善四柱矩阵变压器的EMI问题，但是此类方法须引入至少2a层屏蔽层（a为变压器一次、二次绕组的交错次数），势必会带来额外的高频损耗，不利于变压器效率的提升。因此屏蔽层的固有缺陷限制了此类屏蔽方法的应用范围，学者们将目光转向其他研究方向：文献[15]采用共模噪声抵消的控制方法，提出了一种新的拓扑结构。但是文献[15]仅考虑了一次侧开关管的电压应力和变换器的工作效率，没有深入探讨共模噪声的传导过程。本文将在此拓扑的基础上详细分析共模噪声的抑制原理，并进一步优化拓扑的磁件设计。

本文借鉴了文献[15]提出的拓扑结构，建立了输入侧串联一组反相半桥结构的拓扑，如图1所示，并详细分析了拓扑的工作模态和噪声抵消原理。为了使每个半桥结构的电压脉动点获得相同的幅值，变换器由两个完全相同的LLC单元组成。除了谐振腔的元件参数和变压器相同，输入侧的分压电容C1、C2、C3、C4也要保持大小一致，而且每个LLC单元都符合LLC拓扑的工作特性：变换器工作时，母线上的直流电压经电容分压后分别进入两个逆变桥，被转换成方波电压加到两个谐振腔两端，由于谐振腔的滤波作用，谐振电流可等效成正弦波，再由整流桥将其还原成直流电，最后并联输出，将电能传递给负载。

图1 拓扑原理图 Fig.1 Schematic of the proposed topology

两个LLC单元开关管的开通次序是不同的：当开关管Q1、Q4导通时，Q2、Q3关断，此时，二次侧的同步整流管SR2与SR3导通；反之开关管Q2、Q3导通，Q1、Q4关断，SR1与SR4开始工作。相当于两个半桥结构采用反相控制策略，因此流过两个LLC单元的谐振电流时刻保持反相，构造出的两个电压脉动点幅值相同，相位相反，且幅值减小了一半，因此产生的噪声电流从理论上能够完全抵消。

2 平面变压器的共模噪声

图1所示拓扑可看成两个LLC单元的组合应用，为了深入研究该拓扑的噪声产生机制和噪声传导途径，首先对LLC变换器进行分析。LLC谐振变换器采用变频控制，为了减小磁性元件体积以实现较高的功率密度，变换器的额定工作频率范围通常设置在500kHz以上，因此在电压脉动点存在非常高的电压变化率dv/dt。此外，由于平面变压器绕组的层与层之间正对面积很大、间距却很小，绕组间高度耦合，虽然减小了漏感，寄生电容的作用变得不容忽视[16-17]。根据式（1），变换器工作时存在严重的共模电流。

2.1 噪声源分析

LLC谐振变换器的噪声源如图2所示，对于采用半桥逆变模块和带中心抽头结构变压器的LLC谐振变换器来说，变换器工作时存在4个电压脉动点和两个静态点。谐振腔中的串联谐振电感Lr与变压器一次侧串联，故可被变压器的漏感替代，这样串联谐振电感Lr左侧的脉动点与变压器一次侧的脉动点合并，如图3所示，化简后的拓扑结构共包含3个电压脉动点，每个电压脉动点的作用等效成对应位置的噪声源。为了简化分析，本文假设噪声源相对绕组长度是线性变化的，即绕组上的电位沿长度方向x均匀分布。

图2 LLC谐振变换器的噪声源 Fig.2 CM noise sources of LLC converter

图3 化简后的噪声源示意图 Fig.3 Schematic of simplified CM noise sources

根据矢量的叠加原理（superposition principle），分别分析图4中一次、二次侧的等效噪声源。

图4 变换器一次、二次侧的等效噪声源 Fig.4 Equivalent CM noises on primary side and secondary side of transformer respectively

图4a所示为变压器一次侧的等效噪声源，变压器一次侧的脉动点产生的位移电流，沿着变压器一次、二次侧之间的耦合路径传导至二次侧地，再传回变压器一次侧，形成了循环，因此对变换器的工作性能造成了较大的影响。

变压器二次侧的噪声源如图4b所示，由于带有中心抽头结构的变压器二次侧上下两侧绕组S1、S2处的噪声源幅值在理论上相等，而相位相差180°，如果S1、S2的位置恰好相对于一次绕组对称排布，那么二者的作用相互抵消，不对变换器的电磁稳定性造成影响。此外，一次绕组位置处的噪声源幅值峰值为dvp/dt（vp为变压器一次侧端口处最大电压），大小是二次侧位置的两个噪声源最大幅值的n倍（匝比为n:1:1）。综上所述，一次噪声源占了变压器整体噪声源幅值的绝大部分。

2.2 噪声路径分析

产生噪声的本质原因是变压器的绕组之间、绕组与磁心之间存在电气上的耦合。由于平面变压器绕组间距小，正对面积大，易受临近效应（proximity effect）的影响，在相邻两层绕组之间感应产生寄生电容，而变换器工作时开关管高频动作引入的dv/dt作用于寄生电容两端，对寄生电容进行快速的充放电，因而产生与工作频率同频的位移电流（displacement current），部分位移电流将沿着各传导路径在变换器内部循环，导致严重的EMI问题[18]。

可以说，传导路径是产生EMI问题的关键因素之一，由于变压器的磁心材料实际具有一定的电导率，因此在高频下，磁心会与变压器一次、二次侧产生电气上的耦合，形成寄生电容Cpc、Ccs，以及对地电容Cce。变换器的噪声传导路径如图5所示。图5中标注了四条主要的噪声传导路径：实线表示的是变压器一次侧噪声源沿一次、二次侧之间寄生电容传导的噪声电流Ip-s，虚线代表一次侧噪声源经磁心传导至变压器二次侧的噪声电流Ip-c-s，由于后者占比较小，因此用Cps表示一次、二次绕组间的噪声传导路径。点画线表示一次侧噪声源经磁心和磁心对地电容直接返回输入侧的噪声电流Ip-c。而二次侧噪声源产生的噪声电流Ic-s则直接传导至输出端，不参与变换器内部的循环，故不会带来电磁干扰问题。

图5 变换器的噪声传导路径 Fig.5 Circulation pass of CM noises on converter

两种绕组排布下的Ip-c传导路径如图6所示，如图6b，当变压器绕组的一次侧被置于中间层时，即采用副-原-原-副结构，由于一次绕组与磁心的正对面积仅为绕组的横截面积，一次绕组与变压器磁心的电耦合明显比采用6a所示的原-副-副-原结构的小，因此等效的寄生电容Cpc也很小，相当于抑制了Ip-c的传导路径。根据式（1），虽然Ip-s和Ip-c都是一次侧噪声源产生的，具有相同的dv/dt，但是Ip-c的传导路径被阻碍，使得Ip-c的值远小于Ip-s，故可忽略不计。综上所述，对于采用了副-原-原-副的绕组排布方式的平面变压器来说，变换器的主要噪声是Ip-s和Ip-c-s，下文用共模电流iCM来表示二者之和。

图6 两种绕组排布下的Ip-c传导路径 Fig.6 Circulation pass of Ip-c with two winding layer arrangements of matrix transformer

2.3 共模噪声的预测

单匝绕组的噪声模型如图7a，定义变压器一次绕组两端电位分别为VA、VB，则第i匝绕组两端的电位分别记作VAi、VBi（i=1,2,···,n，变压器匝比为n:1:1）。同样地，假设绕组上的电位沿绕组长度方向均匀分布，且每匝绕组的长度都等于L，那么位于第i匝绕组位置x处的位移Δx对应的寄生电容ΔC可表示为

式中，Cpsi为第i匝一次绕组与相邻的二次绕组之间的层间寄生电容。式（1）可改写成式（3），即每段位移Δx的电容ΔC都对应产生噪声电流ΔiCM(x)。

图7 变压器共模噪声模型 Fig.7 CM noise model of transformer

由于绕组间寄生电容的充放电过程仅发生在死区时间内，那么寄生电容两端电压相对时间的微分和导数存在关系

将式（4）代入式（3），然后积分得到第i匝一次绕组与其相邻的二次绕组耦合产生的共模电流iCMi的幅值为

式（5）表明，变换器输入侧噪声源对每一对一次、二次绕组之间的电容充放电产生的噪声电流iCMi的幅值取决于该匝绕组两端电压微分之和及寄生电容的大小。式（5）同样可以用于表述整个变压器一次侧向二次侧传导的总噪声电流iCM的幅值，如图7b，变压器一次侧两端电位VA=Vin、VB=0。

如果所用的变压器绕组是严格对称的，那么可化简式（6）得到

LLC变换器的励磁电感Lm和串联谐振电感Lr在死区时间内共同参与谐振，由于Lm的电感值比Lr大很多，故并联谐振频率fm远小于串联谐振频率fr，因此在死区时间内im可看作是恒流源，故im对寄生电容放电的速度是保持不变的，所以电容两端电压的变化率也是不变的，电压脉动产生的噪声电流在死区内幅值不变，如图8所示，每个开关周期iCM的波形可看作交替发生的方波信号。

图8 变压器一次电压脉动和对应产生的共模噪声 Fig.8 Voltage pulsation of primary side and the associated CM noise

由于变压器一次侧直接与半桥的中点相连，且为了保证软开关的实现，变换器的寄生电容在死区结束之前就已完成充放电，共模电流iCM的幅值iCM_max的表达式为

对共模噪声iCM进行傅里叶分解，得到iCM的时域表达式为

近日，工业联接领域专家魏德米勒发布新型LUF及LLF系列直插式电源端子，具有高可靠性，免工具接线，快速高效联接等特点。魏德米勒OMNIMATE®电源端子LUF及LLF系列采用可靠的直插式联接技术，为客户提供完美解决方案，可应对行业应用中出现的各种挑战。该系列端子与导线的触点始终自动保持压接和闭合，确保了高可靠安全联接。而且，LUF及LLF系列端子可免工具接线，接线和释放操作简捷、直观，快速高效。产品符合UL 1059的要求，电压可达UL 1 000 V， 轻松应对苛刻的应用环境。

式（9）表明在变换器的共模噪声除了与一次绕组两端的电压、一次、二次绕组层间的寄生电容有关，还受死区时间和频率的影响，因此工作频率越高，变换器的噪声问题越严重。

3 噪声抵消控制方法

图1所示电路输入侧的等效噪声源和噪声传导路径如图9a所示。采用第2节的分析方法，将输入侧的两个噪声源分开讨论，如图9b、图9c所示，可以看到，构造出的两个噪声源不仅相位互补，而且幅值降为原来的一半，实现了一次侧噪声源的相互抵消。

图9 变换器的等效互补噪声源 Fig.9 Equivalent complementary CM noise sources of converter

由于图1的一次侧相当于两个匝比相同的变压器串联，每个流过变压器的噪声都符合式（6），那么输出侧总的噪声幅值为

式中，i、j分别为两个变压器的第i、j匝一次绕组。如果两个变压器采用完全一致的磁心结构和绕组排布设计，一次、二次绕组层间的寄生电容相等，可进一步化简式（10）得到

但是实际上采用噪声抵消控制方法后的共模噪声仍然无法完全抵消，除了变压器存在固有的制作误差外，还可以从时域的角度解释：为了保证LLC变换器实现软开关，一次侧的所有寄生电容，包括开关管两端的寄生电容、线路的杂散电容、变压器的寄生电容都要在死区结束之前完成充放电，变压器一次电压脉动和对应产生的共模噪声如图10所示，寄生电容的充放电时间即为共模噪声的出现时间。

图10中Vds1、Vds2为开关管Q1、Q3两端的电压，iCM1、iCM2分别为ISOP-LLC的两个LLC变换器单元的共模噪声。在虚线框标注的一个死区时段内，两个LLC单元的共模噪声出现的时间不是完全重合的，因此即使两个LLC单元采用反相控制，一次侧噪声源产生的共模电流也不是完全抵消的。

图10 变压器一次电压脉动和对应产生的共模噪声 Fig.10 Voltage pulsation of primary side and the associated CM noise

因此，为了使ISOP-LLC拓扑的共模噪声尽可能降低，各单元变压器的一次、二次绕组间寄生电容大小应尽量保持一致。

4 变换器的磁集成设计

4.1 磁心的集成

为了实现共模噪声的抵消，需要保证两个LLC单元的一次、二次侧寄生电容Cps相等，因此变压器T1、T2宜采用相同的结构。单个变压器的绕组结构如图11所示。T1、T2各具有两个磁柱，实际是两个变压器单元经磁通抵消得到的矩阵变压器[7]。本节所有虚线皆代表电流方向，实线箭头代表一次电流进出变压器绕组的方向。

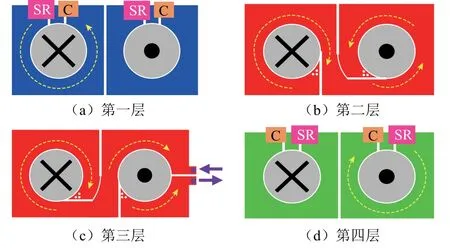
图11 单个变压器的绕组结构 Fig.11 Winding structure of single transformer

综上所述，本文利用ISOP-LLC的特性，实现了两个LLC单元的变压器T1、T2磁心磁集成，集成 后的磁心的磁盘磁通密度降为原来的一半，从而降低了变压器的磁心损耗，有助于变换器效率的提升。

图12 集成前后变压器一次绕组结构 Fig.12 Primary winding before and after integration

4.2 变压器二次绕组的优化设计

由图11a、图11d可知，在变压器单元T1、T2集成之前，两个变压器的二次绕组设计和连接二次侧端口至负载整流元件、滤波电容的排布完全一致。T1、T2集成后，共用同一片磁心，如图12c所示。为了集成后磁心的体积最小，两变压器的绕组须在上、下方向上紧密排布，故中间位置没有放置元件的空间，因此变压器的二次绕组和输出侧元件需要随着磁心的集成相应改动，首先两个变压器单元的二次绕组端口都朝向外侧，集成后变压器的二次绕组结构如图13所示。

图13 集成后变压器的二次绕组结构 Fig.13 Secondary winding structure after integrated

图13中T2的二次绕组是由T1旋转180°得到的，因此T1、T2一次、二次绕组的层间寄生电容仍保持等量关系，不会影响到噪声电流抵消的效果。此外，外部元件的排布使得在每半个周期，每对相邻磁柱的二次绕组均不在同一层导通，保证了变压器磁通的均匀分布。变压器二次绕组的边缘效应如图14a所示，由于高频降压变换器的二次电流比较高，虽然每层导通的绕组旁边的两匝绕组并没有向负载传递能量，但是仍会受到临近效应和边缘效应的影响产生高频损耗。为了尽可能地利用有限的绕组面积，降低二次绕组的电流密度，本文对集成后的二次绕组进行了改进。

根据每个变压器单元的磁通方向，可知二次绕组的电位分布，如图14b所示，图14b中箭头指向 变压器的同名端，可以看出，四个变压器单元二次侧的电位分布是中心对称的，同层的每两匝绕组相邻的部分具有相同的电位，所以图中阴影标注的位置之间的寄生电容不会被充放电。鉴于相邻的二次绕组是交替导通的，从最大程度地利用绕组的导流面积的角度着手，降低二次绕组的等效交流电阻，将相邻绕组的阴影处连接起来，有三种不同的连接方式，如图15a、图15b、图15c所示。由于连接处具有相同的电位分布，连接后阴影位置不会产生环流。

图14 变压器二次绕组的边缘效应和电位分布 Fig.14 Fringing effect and potential distribution of secondary winding

图15 改进的二次绕组结构 Fig.15 Improved secondary winding structure

上述三种连接方式中，方案2、方案3不仅在二次绕组内部构成了连接关系，外部元件也随之连接，造成了不同程度的局部短路，故只有方案1有实际应用价值。

从整个变换器的角度考虑，采用上述方法改进变压器二次绕组，充分地阐释了全波整流结构交替导通的特性，同时结合矩阵变压器的电磁分布规律，在实现文献[15]所提拓扑功能的基础上，合理利用了现有的变压器空间，因此变压器的功率密度不受影响。最重要的是，上述方法使得变压器的铜损降低，有助于提高变换器整体的工作效率。

5 仿真研究

为了验证本文针对ISOP-LLC拓扑提出的变压器磁心集成方法和二次绕组的优化设计，基于电磁仿真软件Maxwell搭建了图16所示的3D模型，并对模型进行了有限元分析。

图16 变压器的3D仿真模型 Fig.16 3D simulated model of the proposed transformer

通过对模型施加外电路激励配合三维瞬态场进行电磁运算，能够较为真实地反映变压器的实际运行情况。图17为仿真得到的变压器的磁通密度分布云图，从图中看到集成后的矩阵变压器的磁通是均匀分布的。

图17 变压器的仿真磁密分布云图 Fig.17 Simulated plot of magetic density distribution

再对改进后的二次绕组涡流场进行仿真，仿真结果如图18所示。可以看到，除了绕组本身，上、下两匝二次绕组连接的部分同样起到了导流的作用，扩大了绕组的实际导流面积，减小了变压器二次侧的电流密度，继而减小了因高频电流产生的等效交流电阻，同时避免了中心抽头变压器的不导通绕组受临近效应影响而产生额外的绕组损耗，能够有效地降低变压器的铜损。

图18 改进后变压器的二次绕组结构的仿真结果 Fig.18 Simulation results of improved secondary winding structure

为了进一步说明本文提出的绕组优化方法的有效性，本文基于同一变压器模型，在不同频率下，对改良前后的二次绕组总损耗进行了仿真。根据仿真数据绘制了额定功率等级下的损耗对比图，如图19所示。

图19 改良前、后二次绕组总损耗对比 Fig.19 Comparison of secondary winding loss between origin and improved

图19表明，在各频率下，改良后的二次绕组损耗明显降低。改良后的二次绕组在1 000kHz下的损耗甚至小于改良前600kHz下的损耗。因此本文提出的优化方法能够缓解同层相邻的两匝二次绕组之间的邻近损耗，有助于变压器整体效率的提升，对变换器的高频化发展有重要的意义。

此外，可以观察到，在频率超过700kHz时，同一工作频率下改良前后的二次绕组损耗差越来越小，即改进后的二次绕组优化效果随频率升高逐步下降。而在500~700kHz的频率范围内改良效果最为显著，变换器额定频率在此范围内选择为宜。最终，本文选择500kHz作为变换器的额定频率，表1列出了变换器的主要参数。

表1 主拓扑的部分参数 Tab.1 The parameters of the proposed prototype

基于表1给出的变换器参数，搭建了一台样机，并给出了实验波形。样机工作于额定500W，输入电压375V、输出电压24V，频率500kHz。实验波形如图20所示，图中，ir1、ir2分别为ISOP-LLC拓扑的两个LLC单元的谐振电流，vGS1、vDS分别为ir1所在LLC单元的上管栅源极、漏源极电压。

图20 实验波形 Fig.20 Experimental waveforms

从图20可以看出，拓扑采用反相控制，由于两个LLC单元在输入侧串联，每个LLC单元的输入电压约为200V，显著降低了一次侧开关器件以及谐振元件的电压应力。此外，变换器能够实现一次侧开关器件的零电压开通，有利于变换器保持较高的变换效率。

需要指出的是，由于高频下，线路、变压器等处存在的寄生电感、寄生电容对变换器的不良影响更显著，以及各模块之间的参数也存在误差，各LLC变压器单元之间的工作状态无法完全一致，因此图20中给出的两个模块的电流波形存在细微差别。未来将针对消除和利用寄生参数，展开研究，使得各单元波形对称性更强。

文献[15]已经证明了四柱磁心结构在提高功率密度和降低磁心损耗方面都更具优势。鉴于文献[15]使用了4个两柱磁心结构的变压器，占用了较大的空间，不利于变压器功率密度的提升。而本文提出的四柱矩阵变压器方案在文献[15]的基础上对二次绕组进行了优化设计，降低了磁心损耗，因此在保证噪声抵消效果的同时，有助于提高变换器的工作效率和功率密度。

6 结论

本文在文献[15]所提拓扑的基础上，提出了一种更为简洁的具有噪声抵消效果的拓扑，并深入研究了噪声源的产生机制和噪声电流的传导路径，进行了共模噪声的预测，并与LLC拓扑的共模噪声进行了对比，证明了该拓扑对变换器噪声控制的抵消作用。为了进一步优化该拓扑的性能，本文采用磁集成技术，对变压器磁心进行了改良。此外，针对二次侧带中心抽头的变压器，提出一种二次绕组的优化设计方法，并利用电磁仿真软件Maxwell搭建变压器的电磁仿真模型和外电路激励模型，进行了仿真对比分析。最后搭建了一台功率500W、频率500kHz的实验样机，验证了所提磁集成方案和二次绕组优化设计的合理性和可行性。