电力系统低模型耦合智能状态估计

赵化时，李 胜，林子杰，何宇斌，周华锋，陈根军，胡斯佳，曹一家

(1.中国南方电网电力调度控制中心，广东 广州 510623；2.湖南大学电气与信息工程学院，湖南 长沙 410082；3.南京南瑞继保电气有限公司，江苏 南京 211102)

电力系统状态估计(state estimation，SE)利用量测系统提供的冗余信息，根据相应估计准则，自动剔除不良量测数据，消除或减少随机干扰、装置故障和人为误操作引入的误差信息，得出当前条件下最逼近量测真值的系统状态，从而达到“提纯”数据的目的，SE是现代能量管理系统的重要组成部分。20世纪70年代，麻省理工学院的F. C. Schweppe教授首次将采用加权最小二乘法(weighted least square, WLS)的SE思想引入电力系统监控体系[1]，随后WLS-SE技术逐渐成为电力系统状态估计的主流，并得到广泛应用[2]。

电力系统潮流计算是状态估计的特例[2]，在潮流计算中，提高迭代的收敛性和鲁棒性一直是它的一个重要研究课题[3-4]。针对大规模交直流电网潮流计算收敛困难的问题，文献[5]引入步长优化因子大幅改善了迭代的收敛性，并能较好地处理病态系统的潮流；在交直流系统的潮流计算中，文献[6]在步长优化乘子中引入了混合乘子，获得了较好的计算性能；文献[7]将最优乘子引入电流注入型保留非线性潮流计算，提高了潮流计算的收敛性与速度。

相对于变步长潮流计算，传统WLS-SE算法的步长因子常设定为1，此外，其修正方程增益矩阵的条件数是其量测方程雅克比矩阵条件数的平方。因此，与潮流计算相比，状态估计在迭代计算的数值结构上“先天不足”[1]。考虑到实践中状态估计常面临量测数据质量偏低、量测缺失、网络条件复杂等情况，传统定步长WLS-SE算法很难在收敛性、估计质量和运算速度上同时获得优良的效果。

为改善SE的收敛性能，文献[8]从解析角度提出了SE最优乘子，获得了较好的收敛性和计算效率；文献[9]进一步验证了该方法对检测、识别和消除坏数据的适应性；文献[10]考虑了目标函数条件预处理的影响。虽然文献[8-10]在SE中采用的最优乘子法各有特点，但这些基于“解析法”的步长调整策略都与电力系统的数学模型紧密联系，每次迭代都必须精确求得与模型高度耦合的步长因子，演算过程较为复杂、计算量偏大；而且，若电力系统结构、参数的变化导致其数学模型发生改变，将直接影响其运算性能。此外，实际系统的数学模型可能会表现出一定“病态”并存在不良数据(如快速发展中的电网)，在该条件下进行状态估计，因网络存在一定数值缺陷且外界输入真假难辨，SE的迭代过程可能会表现出收敛慢、震荡、发散等异常情况。目前尚无文献对上述情况下的SE进行研究。

虽然步长的变化有利于提高SE的收敛性，但仅通过SE本身无法抑制量测系统中不良数据的影响，为提高SE抵御不良数据的能力，基于抗差理论[11]，文献[12-14]通过引入权函数在迭代的过程中对状态变量的权重进行自动调整，取得了较好效果。然而，该类方法一般不具备步长调整能力，其性能还有进一步提高的空间。

为提高SE在上述情况下的数值稳定性、估计质量和电网适配性，考虑采用变权操作可抵御不良数据的影响，本文首先在WLS-SE上建立基于IGG抗差法的变权状态估计模型。受经典逻辑函数图像(logistic function, LF)[15-17]的启发，本文重点研究状态估计的步长调整技术，通过对传统LF进行重构，找到在“形状”上与状态估计高质量数值迭代具有天然适配性的“母函数”，并将其作为步长控制因子，设定母函数的形状控制参数，并使其中部分可通过“迭代效果”进行实时“智能”调整，母函数的“形状”会自动适配调整至符合高质量状态估计数值计算的状态。因该过程无需网络模型的直接“介入”，故该方法对电网的数学模型表现出低耦合性，相对于解析法，其本身也将更易于理解和掌握，并具有更好的可移植性。最后，通过含不良数据和准病态、病态条件的算例分析，验证本文所提方法的有效性。

1 原理简述

1.1 WLS状态估计

在电力系统状态估计中，量测方程表示为

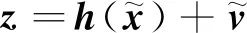
(1)

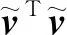
(2)

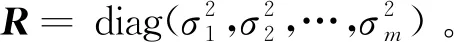
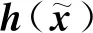
(3)

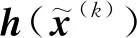
(4)

本文在直角坐标系下对系统进行数学描述和求解。在求解SE问题时，暂不考虑权重的影响(令R为单位矩阵)，从式(3)的第2式可观察到：

(5)

式中κ(*)表示“矩阵*”的条件数。

式(5)说明WLS-SE技术在本质上具有比潮流计算更“脆弱”的数值稳定性[2, 20]；在一定条件下，SE解算过程可能会较潮流计算更易表现出收敛缓慢、估计值不准确甚至不收敛等问题。

1.2 变权重WLS-SE

为提升状态估计在不良数据条件下的估计质量，可在经典WLS-SE算法中植入适当权函数，抗差最小二乘估计[11]是通过等价权将抗差估计理论与最小二乘法紧密结合的算法，能满足上述要求。该类算法在数学格式上与WLS-SE保持一致，仅在权重上有不同含义，即经典WLS-SE的权重是根据量测设备的精度先验确定的，而抗差最小二乘估计的权重是残差的函数。本文基于IGG抗差法对权重进行调整，其权因子函数[14]为

(6)

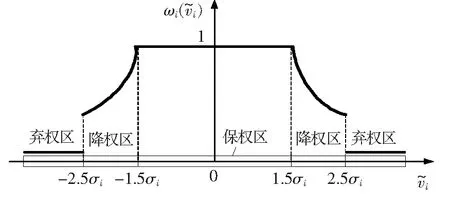
图1 IGG抗差法权因子函数Figure 1 IGG robust method weight factor function

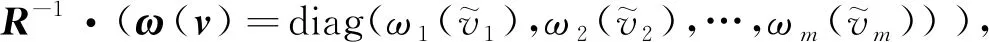
(7)

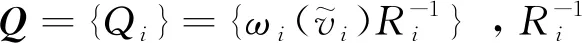
2 步长智能调整

2.1 基本思想

1) 在迭代开端，为加快收敛速度，可选择大于1的步长因子，但步长过大易造成迭代震荡或发散；

基于迭代三原则，本文在式(3)的第1式中引入步长因子λ，即

(8)

在传统方法中，λ是一个与系统模型高度相关的量，为在提高迭代质量的前提下降低运算复杂度，本文提出以下观点：

1) 一个良好设计的λ需在迭代过程中较好地满足迭代三原则；

通过分析发现，LF的形状具有同时满足2个观点的潜力。yLF定义[15-17]为

(9)

该函数关于点(0,0.5)奇对称，在0～1之间取值，形似英文字母S，在深度学习中具有重要应用[22-23]。

2.2 具体策略

Δx=max|Δx|

(10)

为了使yLF更具可控性，进而能较好满足迭代三原则，引入n、a、b、α和β共5个控制参数，将式(9)所示基本yLF“重构”(已将因变量用λ代替，自变量替换为Δx)，并称其为“母函数”，即

Δx∈R

(11)

取n为自由变量，其他4个参数固定为1，式(11)的图像如图2所示，当n>1时，λ与Δx的关系与迭代三原则具有天然适配性。进一步观察，n越大，算法在迭代尾声将获得更小的步长(λ较小)，密集的迭代有利于提高状态估计的收敛性，但也会增加计算时间。鉴于此，对于网络较弱的系统(HTH条件数较大)可适当增大n；对于网络较健壮的系统(HTH条件数相对较小)可通过适当降低n使其迭代尾声的步长缓慢减小，迭代次数和计算时间也会降低。对于本文研究的系统(如图3所示)，通过离线仿真发现n=3可获得较好的迭代性能，因此，后文将暂且将n固定为3进行讨论，当n取其他值时讨论过程类似。

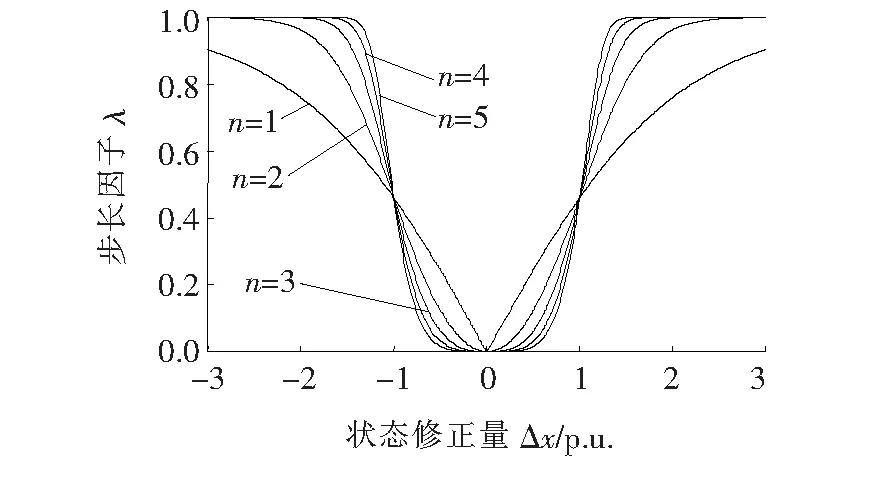
图2 不同n条件下的母函数图像Figure 2 The curves of generating function in different n

图3 IEEE 30节点网络量测配置Figure 3 IEEE 30 node network measurement configuration

在固定n=3的前提下，分别在a为变量、β=b=α=1，β为变量、a=b=α=1，b为变量、a=β=α=1，α为变量、a=β=b=1这4种情况下绘制函数图形，λ与Δx的关系如图4(a)～(d)所示，可以看出，在n=3的前提下，参数a和β主要控制λ的取值范围(图4(a)、(b))，为方便设计，在式(11)中可将a固定为1，仅通过β来控制λ的取值范围。此外，从图4(c)～(d)可以观察到，参数b和α主要控制函数的形状，考虑到α对曲线形状的影响更大，可令式(11)中的b=1，仅通过α来调整函数形状。基于以上分析，式(11)可进一步变化为

Δx∈R

(12)

当第k步状态修正量Δx(k)>Δx(k-1)时，表明状态修正量正在增大，此时第k步的步长因子λ(k)应朝增大的方向变化，以加快收敛速度；当Δx(k)<Δx(k-1)时，λ(k)应缓慢减小，实现算法的稳定收敛。仔细观察图4(d)可知，当Δx固定时，参数α的变化与λ的变化正相关，因此，第k步α的值α(k)也应随着状态修正量的变化而变化，以进一步在迭代的过程中优化λ的调整。令：

(13)

可使迭代过程中的α满足迭代要求。

此外，数字滤波的研究显示，状态修正量的Δx(k)Δx(k-1)能有效去除噪声对估计结果的影响[24]。可引入中间变量p(k)作为自相关Δx(k)Δx(k-1)的估计：

p(k)=γp(k-1)+(1-γ)Δx(k)Δx(k-1)

(14)

其中γ∈(0,1)为权系数，其取值一般接近1，用来控制收敛速度。可使λ的变化根据Δx(k)Δx(k-1)估计的平均值迭代变化。将式(12)中的Δx换成中间变量p(k)，可实现用Δx(k)Δx(k-1)间接调整λ。

图4 控制参数对改进母函数图像的影响(n=3)Figure 4 The influence of the control parameters to the shape of the improved generating function (n=3)

由式(12)～(14)经一定化简计算可得本文所提算法步长因子的迭代格式：

(15)

式中β∈(0,2]可使迭代初始阶段获得较大的λ。

结合式(3)、(7)、(8)、(15)，可得本文所提SE的迭代方程为

(16)

基于以上讨论，所提算法的流程如图5所示，在每次迭代过程中算法先对权重进行调整(“变权操作算法”模块)，当权重调整至最佳状态后，此时系统已较好地削弱了不良数据的影响，再根据“迭代效果”直接对状态估计的步长因子进行智能调整，从而进行高质量数值计算(“智能步长调整算法”模块)，直至状态修正量达到收敛条件(因初值需要，应预先进行一步基于式(3)的基本WLS-SE迭代)。

图5 状态估计流程Figure 5 State estimation flow chart

3 算例分析

IEEE 30节点网络量测配置见图3。为了验证本文所提算法的有效性，基于Matlab平台并以IEEE 30节点系统[25]作为研究对象，分别对比传统固定步长固定权重(fixed step size WLS，FSSWLS)、变步长固定权重(adaptive step size WLS，ASSWLS)、固定步长变权重(weighting fixed step size WLS，WFSSWLS)和本文所提出的变步长变权重(weighting adaptive step size WLS，WASSWLS)WLS-SE算法的收敛性能和估计质量(变权重中权因子函数、ASSWLS和WFSSWLS中变步长的表达式分别见式(6)、(15))。

3.1 量测出现不良数据(算例1)

为读取数据方便，本文将IEEE 30节点系统中的节点1和30互换，并将新的节点30作为平衡节点，其他节点和线路等参数保持不变。设定电压、支路功率、节点注入功率量测的σ分别为0.004、0.008、0.01 p.u.(零功率注入节点的σ为0.000 1 p.u.)，取ε=10-6。以潮流计算结果作为真值，正常量测值是真值1.5个标准差内的随机修改量(见图1保权区边界)。本算例所用不良量测数据的设置如图3标注和表1所示。

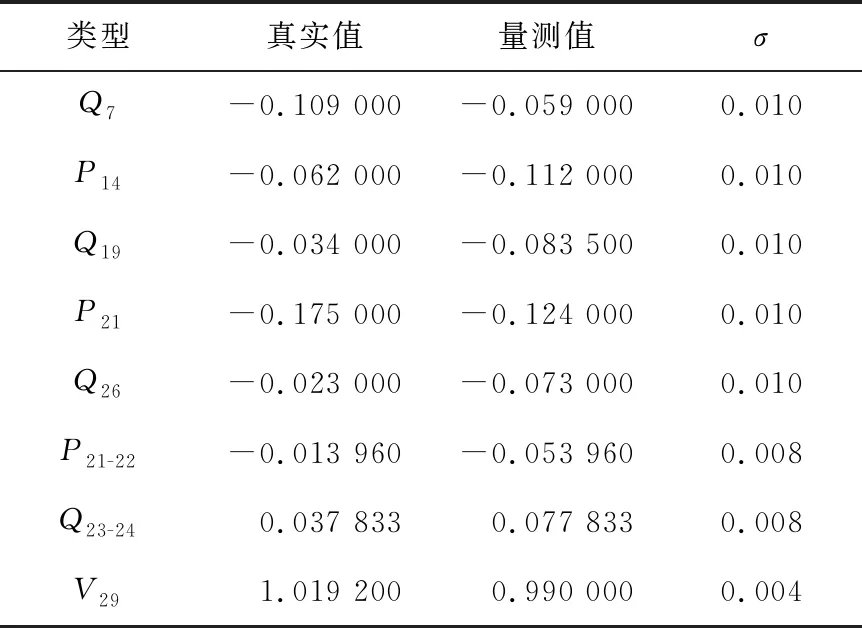
表1 不良数据设置Table 1 Bad data setting p.u.

在具体执行式(16)时，参数β、γ、p(k)初始值p(0)的选取会对迭代性能产生影响。为获得参数的最佳值，本文在主程序外层编写3个for循环对β、γ、p(0)在各自取值范围内进行滚动搜索(参数取值范围：β∈[1,2.5]，γ∈[0.90,0.98]，p(0)∈[1,2.5])。程序每运行到一组β、γ、p(0)都自动记录下算法的迭代次数和估计精度，对应迭代次数最少、估计精度最高者即为3个参数的最佳值。经过程序自动筛选，本文最终确定p(0)=2.0、β=2.0、γ=0.95，这些参数对迭代产生的影响如图6所示(β、γ、p(0)中任何一个参数发生变化，其他2个参数均固定为通过for循环最终确定的最佳值)。

由图6可知，β、γ、p(0)对算法的收敛性能影响较大，适当增大β、γ、p(0)将有利于提高收敛性能，但通过仿真也发现参数的取值过大或过小都不利于收敛。实际上，由式(15)可知β、γ、p(0)与λ表现出正相关特性，因此，β、γ、p(0)的取值在一定程度上反映了λ的大小，由文2.1中的迭代三原则可知，过大或者过小的λ均不利于收敛。因此，β、γ、p(0)的取值也存在一定范围，这将由具体网络条件决定。

图6 不同控制参数下算法的收敛过程Figure 6 Algorithm convergence process with different key parameters

FSSWLS、WFSSWLS、ASSWLS和本文所提WASSWLS算法的收敛过程如图7所示，4种算法的电压幅值和相角的初值分别为1.05、0，对于ASSWLS和WASSWLS算法，Δx(k-1)的初始值为1，p(0)=2.0、β=2.0、γ=0.95。此外，在计算过程中，为防止α变化太大致使母函数的形状变化剧烈，本文对α的限幅措施：当α(k)<0.2时，取α(k)=0.2；当α(k)>10时，取α(k)=10。

由图7可知，ASSWLS的迭代次数小于FSSWLS算法，且其收敛曲线全程低于FSSWLS，这说明本文所提的步长调整策略有利于加快收敛。此外，WFSSWLS的迭代次数低于FSSWLS算法，这说明对于一个存在不良数据但数值结构健壮的网络，通过变权操作筛查量测中的不良数据也有利于加速收敛；对比文中曲线可发现WASSWLS较ASSWLS具有更为优良的收敛特性，这说明在进行步长调整的情况下，调整权重有利于进一步提高SE的收敛性能，同时，也证明了本文提出的步长和权重调整策略是互相兼容的；WFSSWLS的收敛次数略低于ASSWLS(两者收敛曲线接近)，考虑到前者只进行了变权操作，后者只进行了变步长操作，这说明对于一个存在不良数据但数值结构健壮的网络，抑制不良数据和调整步长在提升迭代性能上具有一定等效性，有时前者的作用会更明显(网络趋坏的条件下调步长的作用优于调权重)。最后，WASSWLS和WFSSWLS的收敛曲线比较接近(实际上如表2所示，WASSWLS的收敛性能略好于WFSSWLS算法)，这一方面再次证明了上述论断；另一方面，WASSWLS算法所对应的Δx较ASSWLS以更为

表2 估计质量(不良数据条件)Table 2 Estimation quality (bad data condition)

“缓和”的方式趋于收敛门槛值，这与文2.1中所提的“迭代三原则”是相匹配的，有利于提高迭代质量(表2)。

FSSWLS、ASSWLS、WFSSWLS和WASSWLS这4种算法中λ与迭代次数的关系曲线如图8所示(因初值需要，WASSWLS中仅在首次迭代中使用了式(3)的格式，后续过程均采用式(16)的格式进行迭代)，在初始阶段ASSWLS和WASSWLS的λ明显大于1(WASSWLS第1次迭代除外)，有利于加快收敛。随后，λ随Δx的减小逐渐降低，当迭代进行到第3或者第4次时，两者的λ开始小于1；当迭代进入尾声，λ逐渐趋于平缓，与之对应，图7中的Δx也平缓变化，这有利于提高估计质量(分别对比表2中数据)。

图8 步长因子变化过程Figure 8 Variation process of step size factor

分别引入平均估计误差S1和平均最大估计误差S2，对所提算法的估计质量进行综合评估[26]，S1和S2的数值越小说明估计精度越高。

(17)

(18)

图9 迭代过程中WASSWLS不良数据点的权重(算例1)Figure 9 The weight of bad data point during iteration in case1 by using of WASSWLS

通过20次状态估计(对应20个随机输入数据断面)，FSSWLS、ASSWLS、WFSSWLS和WASSWLS所对应的S1、S2见表2，可知在20个数据断面中，采用本文所提的WASSWLS算法，其S1、S2、平均迭代次数以及平均迭代时间是4种算法中最优的。进一步观察会发现，WASSWLS算法平均仅需迭代8.1次就使S1较其他3种算法高出一个数量级，这充分证明了本文所提方法在估计质量和运算效率上的优势。

某一典型输入数据断面下30个节点(图3)电压幅值的估计结果如图10所示，可以观察到，采用变权操作的WASSWLS和WFSSWLS所对应的估计值更接近真值(表2的数值指出WASSWLS最接近真值)，该图从直观上验证了本文所提算法在估计质量上的优势。

图10 某一典型数据断面节点电压幅值估计结果Figure 10 Voltage magnitude estimation result of a typic input data section

需要说明的是，与经典不良数据检测、辨识技术(如“J检测法[2]”)不同，所提算法在每一步迭代中都采用了变权重的方法来剔除(或削弱)“不良数据”对状态估计结果的影响。所以本算例也验证了量测“不良”时本文所提WASSWLS算法的有效性。

3.2 准病态条件(算例2)

在电力系统接近病态条件下(“准病态”)，为了验证本文所提算法的性能，对算例1中IEEE 30节点的支路参数进行修改(保持X不变，增大线路的R/X值[27])，如表3所示，用以模拟系统在准病态条件下的状态估计。算例1中FSSWLS迭代方程的条件数为1.622 1×106(式(5))，按表3修改线路参数后其条件数增加至2.54×108，这说明系统已处于更差的数值计算状态。在该条件下，采用FSSWLS、ASSWLS、WFSSWLS和WASSWLS算法进行状态估计得到如图11所示的收敛特性。

观察图11可知，采用FSSWLS算法，系统的迭代次数从线路参数修改前的11次(图7)增加到了此时的15次，WFSSWLS从修改前的8次(图7)增加到了此时的12次，这是系统数值稳定性变差后的必然结果。然而，采用对步长进行智能调整的ASSWLS、WASSWLS算法，其迭代次数仅较图7略有增加(1次)。进一步观察还会发现，采用变步长的ASSWLS和WASSWLS其收敛次数都比只有变权操作的WFSSWLS低，这与图7是不同的，说明在网络数值条件趋坏的条件下，本文所提的步长调整策略在提高SE解算过程的鲁棒性上较变权操作更具优势。此外，在图11中，WASSWLS和ASSWLS算法在迭代初始阶段Δx较大，迭代进入尾声时Δx趋缓收敛于停止条件，这与文2.1中所提的理想迭代三原则相吻合，有利于提高迭代质量(分别对比表4所示数据)。

表3 修改前、后线路的参数配置Table 3 Line’s parameter before and after modification

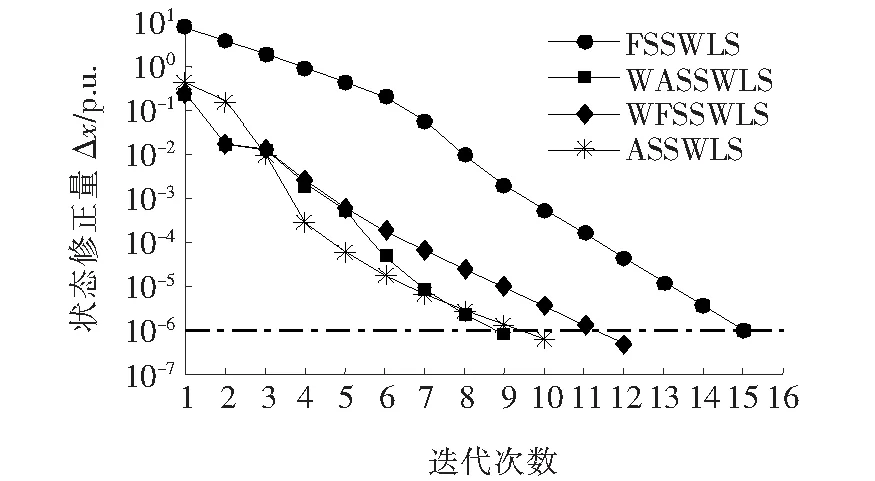
图11 准病态条件下的收敛过程Figure 11 Convergence process under quasi-ill-condition

表4 估计质量(准病态条件)Table 4 Estimation quality (quasi-ill-conditioned)

算例2中λ的变化特性如图12所示。与算例1不同的是，ASSWLS和WASSWLS算法的λ开始小于1时的迭代次数均较图8增加了1次；类似之处是，当进入迭代尾声，2种算法λ的减小趋于平缓，与之对应，Δx也在此阶段平缓变化(图11)。算例2中WASSWLS不良数据点的权重与迭代次数的关系与算例1完全相同(图9)，如图13所示，这说明在网络趋坏的条件下，本文所提算法对不良数据的筛选能力没有发生变化。

图12 步长因子变化过程Figure 12 Variation process of step size factor

图13 迭代过程中WASSWLS不良数据的权重Figure 13 The weight of bad data point during iteration by using of WASSWLS

按表3变更网络参数后20个数据断面下系统的估计质量见表4。对比表2、4可知，当网络数值条件进入“准病态”后，其所对应的S1、平均迭代次数以及平均迭代时间较表2中的对等项都有明显的增加，其中，WASSWLS算法增加得最少、ASSWLS次之、WFSSWLS最多。同时，WASSWLS算法的S1、S2均小于其他3种算法，迭代质量较为满意。

通过分析准病态条件下的估计结果可知，步长固定的FSSWLS和WFSSWLS算法对系统数学模型的变化表现出了较强的敏感性，相较之下，WASSWLS和ASSWLS算法因解算过程步长的变化由状态修正量决定而不与系统模型产生直接联系，在整个迭代过程中仍保持了较好的稳定性和较高的估计质量。另外，表4显示，虽然WFSSWLS的平均迭代次数远高于WASSWLS，但其S1、S2却与WASSWLS差距不大且明显小于FSSWLS算法，说明：①变权操作在提高SE估计准确性上作用明显，这是因为权重的调整抵御了大部分不良数据对估计精度的影响，可从图14中WASSWLS、ASSWLS对应曲线较为接近也可以得到验证；②变步长操作在抵御电力系统模型的“趋坏”、提高状态估计的收敛性上起主要作用。

图14为与算例2对应的某一典型输入数据断面下各节点电压幅值的估计值，与算例1中的图10相比，FSSWLS、ASSWLS、WFSSWLS和WASSWLS算法的估计结果均在一定程度上进一步远离了真值，但总体来说，WASSWLS所对应的曲线更接近真值曲线。在系统处于准病态条件下，该图从直观上进一步验证了本文所提WASSWLS算法仍具有良好的估计质量。

图14 某一典型数据断面节点电压幅值估计结果Figure 14 Voltage magnitude estimation result of a typic input data section

3.3 病态条件(算例3)

为进一步展示本文所提算法的特性，在表3的基础上进一步修改部分线路的电阻参数，如表5所示，将HTH的条件数进一步提高到6.810 7×1012。

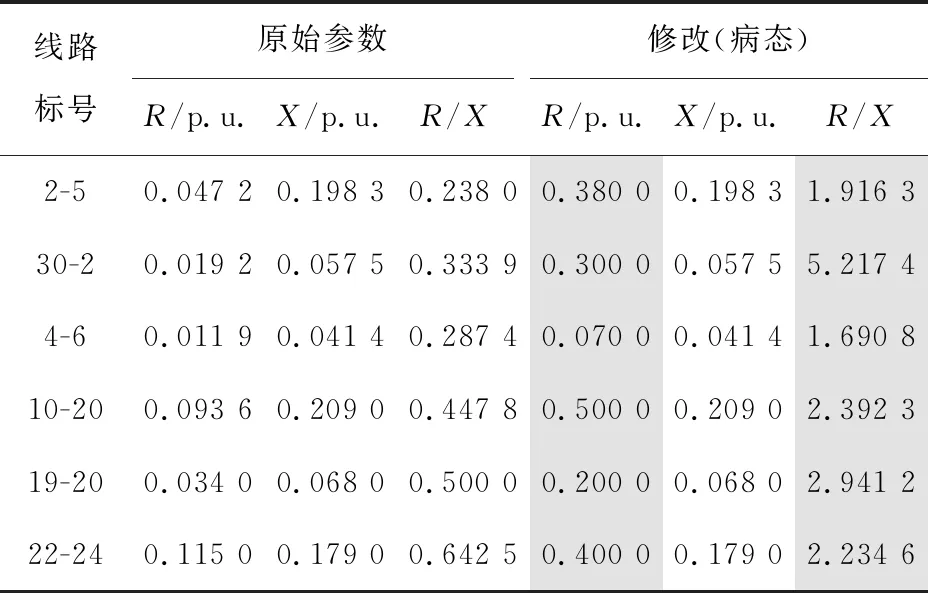
表5 修改前、后线路的参数配置Table 5 Line’s parameter before and after modification

在病态条件下，采用FSSWLS、ASSWLS、WFSSWLS和WASSWLS的收敛过程如图15所示，显然，采用FSSWLS算法迭代已不再收敛，系统进入数值上的“病态”。采用WFSSWLS算法时迭代过程表现出大幅震荡和收敛迟缓，计算过程在某种程度上趋于临界不收敛状态，最终需要17次迭代；ASSWLS需要15次迭代能够收敛，而此时的WASSWLS算法只需13次迭代即可收敛，且从图15、16可知，即使在这种“恶劣”的条件下，采用WASSWLS和ASSWLS算法的Δx和λ仍然表现出符合理想迭代的变化趋势，计算的鲁棒性较好(因WFSSWLS和WASSWLS的权重调整情况与图9、13完全相同，不再赘述)。

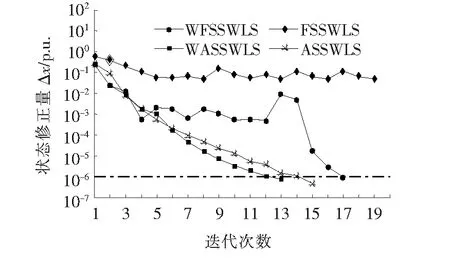
图15 病态条件下的收敛过程Figure 15 Convergence process under ill-conditioned

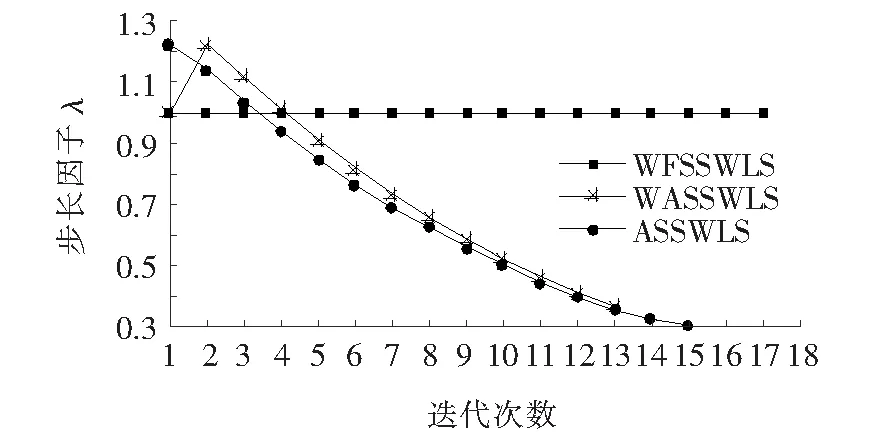
图16 步长因子变化过程Figure 16 Variation process of step size factor

在病态条件下，ASSWLS、WFSSWLS以及WASSWLS这3种算法在某一典型数据断面的节点电压幅值估计结果如图17所示(因FSSWLS不收敛，故未绘制在图17中)，基于20个随机数据断面的估计质量如表6所示。

图17 某一典型数据断面节点电压幅值估计结果Figure 17 Voltage magnitude estimation result of a typic input data section

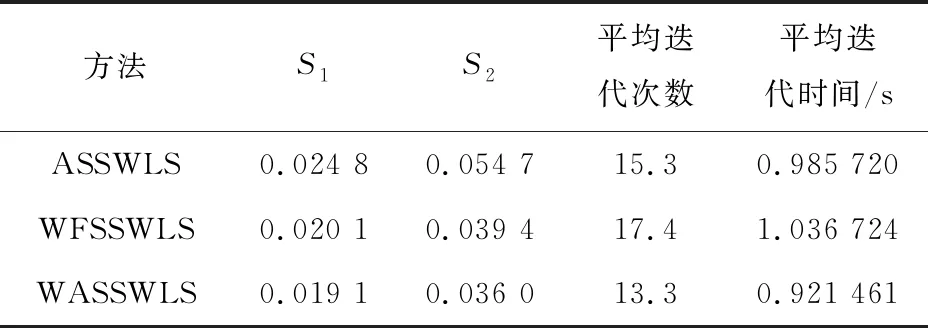
表6 估计质量(病态条件)Table 6 Estimation quality (ill-conditioned)

综合图15、17和表6可知，WASSWLS算法的S1、S2、平均迭代次数以及平均迭代时间说明：在系统处于病态条件下，其迭代速度和估计质量均较ASSWLS、WFSSWLS优良。与算例2类似，观察表6可知，虽然WFSSWLS算法的平均迭代次数高于WASSWLS，但它们的S1和S2差别不大，说明权重的调整在控制估计精度上起主要作用，这从图17中WFSSWLS、WASSWLS对应曲线较为接近也可以得到验证，而步长的智能调整则对状态估计的收敛性起主要作用，这与算例2所得结论一致。

通过算例2、3可以证实本文所提WASSWLS方法在网络准病态、病态条件下具有较好的数值稳定性和估计质量。本文所提步长调整算法对电力系统数学模型的耦合性较低，步长因子只取决于当前和历史迭代效果(式(16))；同时，权重的调整又降低了不良数据对估计结果的影响。因此，可以说所提算法对网络条件的变化具有较强适应性。

4 结语

通过所构建的母函数，本文提出并重点研究了一种对模型耦合性较低且可进行权重自动调整的电力系统状态估计方法。基于IEEE 30节点系统分别讨论了当量测出现不良数据、系统准病态和病态3种情况下的状态估计结果，得到如下结论：

1) 因迭代过程会根据迭代效果“智能”调整至符合健壮数值计算的状态，在收敛性、估计质量和运算效率上，本文所提算法均明显优于传统方法；

2) 本文所提算法具有低模型耦合性，在维持优良迭代性能的前提下，其迭代过程对电力系统数学模型的“趋坏”表现不敏感，数值稳定性高、估计质量优良；

3) 本文所提步长调整策略与变权操作具有兼容性，能在获得较高数值运算性能的条件下抵御不良数据的影响，估计结果精度高。