基于注意力机制与深度学习算法的机床主轴系统故障辨识
王伟平, 王琦,2, 于洋
(1.沈阳工业大学 信息科学与工程学院, 辽宁 沈阳 110870; 2.辽宁工业大学, 辽宁 锦州 121001)
0 引言
数控机床是工业母机,是整个装备制造业的核心基础装备,在国防武器、航空航天、航母舰船等军事工业领域以及民用工业领域的零部件加工中发挥着重要的基石作用。
智能时代下,智能化检测分析在机床故障诊断研究方面的重要作用日益凸显。主轴系统是机床最重要的组成部分,做好针对主轴系统的故障辨识研究,有助于提升机床整体切削能力和使用可靠性。
机床等机械设备的振动往往会影响其工作精度,加速机器的磨损。对振动进行控制是机械管理中不可或缺的部分。故障诊断是得到关于装备运行和故障状况综合评价结果的过程。杨周等基于潜在失效模式与后果分析,提出一种考虑故障相关性的综合方法。王福元等提出一种基于多系统集成的控制策略与故障诊断方法。邓超等建立了基于阈值分布的机床剩余寿命预测模型和概率密度函数。林滨等针对薄壁件切削颤振问题研究了主轴转速变化规律,总结出系统稳定性极限图。常丽萍等研究了轴承内圈倾斜角对轴承振动故障的影响。Prabhu Raja等通过建立机床主轴箱有限元模型,进行了主轴箱热误差最小化策略研究。邱继伟等提出一种自适应共轭非线性近似方法以解决结构可靠性问题。Sheng等利用有限元分析软件对数控机床主轴的静、动态特性进行了分析。Zhao等研究了如何能够准确地模拟主轴热误差的方法。高峰等通过设计转子偏心振动方程探究了由于电主轴偏心所导致的转子机械振动特性问题。
上述对于数控机床主轴系统的分析、诊断及健康管理研究,多数是基于理论设计方面或固有机械特性方面,难以满足动态、复杂非线性主轴系统实际在线研究的需要。
近年来,随着机器学习在振动检测分析方面的应用,机械振动非线性检测领域出现了基于深度学习方法的新的研究发展趋势。Tian等提出基于局部均值分解和奇异值分解以及极限学习机的变工况滚动轴承故障诊断。Lu等提出基于层次卷积网络的滚动轴承智能故障诊断及健康状态分类。Ding等提出基于深度Q网络健康状态分类的旋转机械智能故障诊断方法。Lu等提出基于叠加去噪自编码器的旋转机械部件故障诊断方法。Tran等基于支持向量机和人工神经网络提出了齿轮损伤检测策略。Sharma等通过声发射建模进行了轴承故障诊断。朱敏等基于优化核超限学习机的方法提升了故障诊断准确率。Yang等采用二元免疫遗传算法对滚动轴承进行了故障诊断。
然而,上述对单一机械部件的研究也无法反映多部件组合体的故障特点。主轴系统是由多部件组成的复杂非线性组合体,该特点决定其与普通单一旋转机械部件有很大的差异。
为从动态变化、全局特点、局部特征、复杂性、非线性兼顾的角度研究机床主轴系统的故障辨识问题,本文设计了将全局纵向相关度推理感知,与局部横向关键细节的细粒度准确分析有机结合起来的注意力机制研究框架。在框架内,根据主轴系统特有的多部件动态连续性特点,建立了基于循环神经网络的动态推理诊断模型;针对精加工时对机床主轴系统精度要求高、故障辨识难度大的特点,使用分类辨识度高的卷积神经网络进行局部的细粒度辨识。最后,通过机床主轴系统实际使用中的平行不对中、共振等典型故障,以及负载加工状态下的故障辨识,验证了所提框架及模型方法的有效性与优越性。
1 机床主轴系统的故障特征
1.1 主轴系统的非线性特点
机床的主轴系统是由多个部件组成的复杂机电系统(见图1)。其组成部件的固有频率各异,且实际使用中固有频率、机电特性会随使用情况和退化情况发生变化,因此,主轴系统的复杂性、非线性特点决定了其故障诊断研究的难度非常大。
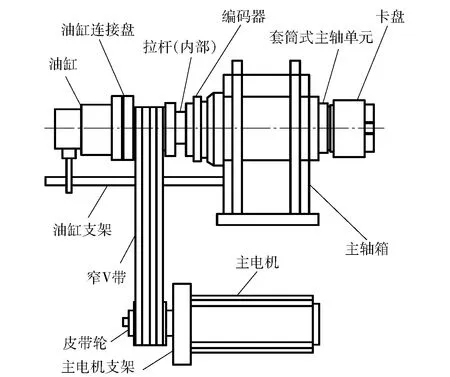
图1 主轴系统Fig.1 Spindle system
1.2 故障特征
主轴系统动态回转特征的变化是其故障特征研究的核心,也是该领域故障诊断的难点。与普通回转类机械结构相比,主轴系统的典型故障特征如下:
1)转速连续性:主轴系统转速数值上具备连续性,使其各转速的动态故障特征具备强相关性。
2)故障区段性:根据主电机的恒功率区、恒扭矩区特点、机械设计特点以及机床加工需要,通常将转速区间划分为粗加工区间、精加工区间等功能区段,进而形成各功能区段的故障区段性特征。
3)故障的分散性:主轴系统因其组件的复杂耦合性、故障的随机性,会在不确定的某一或某几个转速区间段出现局部共振等故障,但在其他转速段该故障消失,表现出故障的分散性与不确定性。
4)故障的整体性:主轴系统会因其组件的不同轴或轴承研伤等结构变化损伤,出现全局性故障,此时会表现出故障的整体性。
5)精度的差异:主轴系统的实际使用要求,决定其各功能区间段对主轴精度的要求存在差异,对故障的辨识也存在关注度、侧重点的差异。
2 算法建模与特征值提取
2.1 基于注意力机制的研究框架建模
1)注意力机制。注意力机制,是解决图像识别、语音信号识别、自然语言处理等领域问题的一种分析技术。其原理源于人类视觉系统的选择性关注机理。人类的视觉系统可以快速地扫描整个图像,并快速地定位期待的主要区域,即先了解全貌,再关注重点,面与点的结合可以更加精准、快速地辨识事物。细粒度是对分析对象的精细化分,目的是更加科学准确合理地深入把握研究的目标,细分出更多的对象细节。
注意力机制、细粒度划分对于认识问题,具有全局辨识和细节关注的双重优势。
2)本文研究框架。本文基于注意力机制的理论特点,结合主轴系统在全局、局部研究的需要,利用所使用深度学习算法的推理、辨识特点,创新性地将图像处理领域中的注意力机制引入到复杂非线性主轴系统的研究中,设计了本文的研究框架(见图2)。力求从纵向全局渐变趋势辨识和横向局部细粒度辨识两个相互关联维度,提高主轴系统故障辨识的效率和准确性。
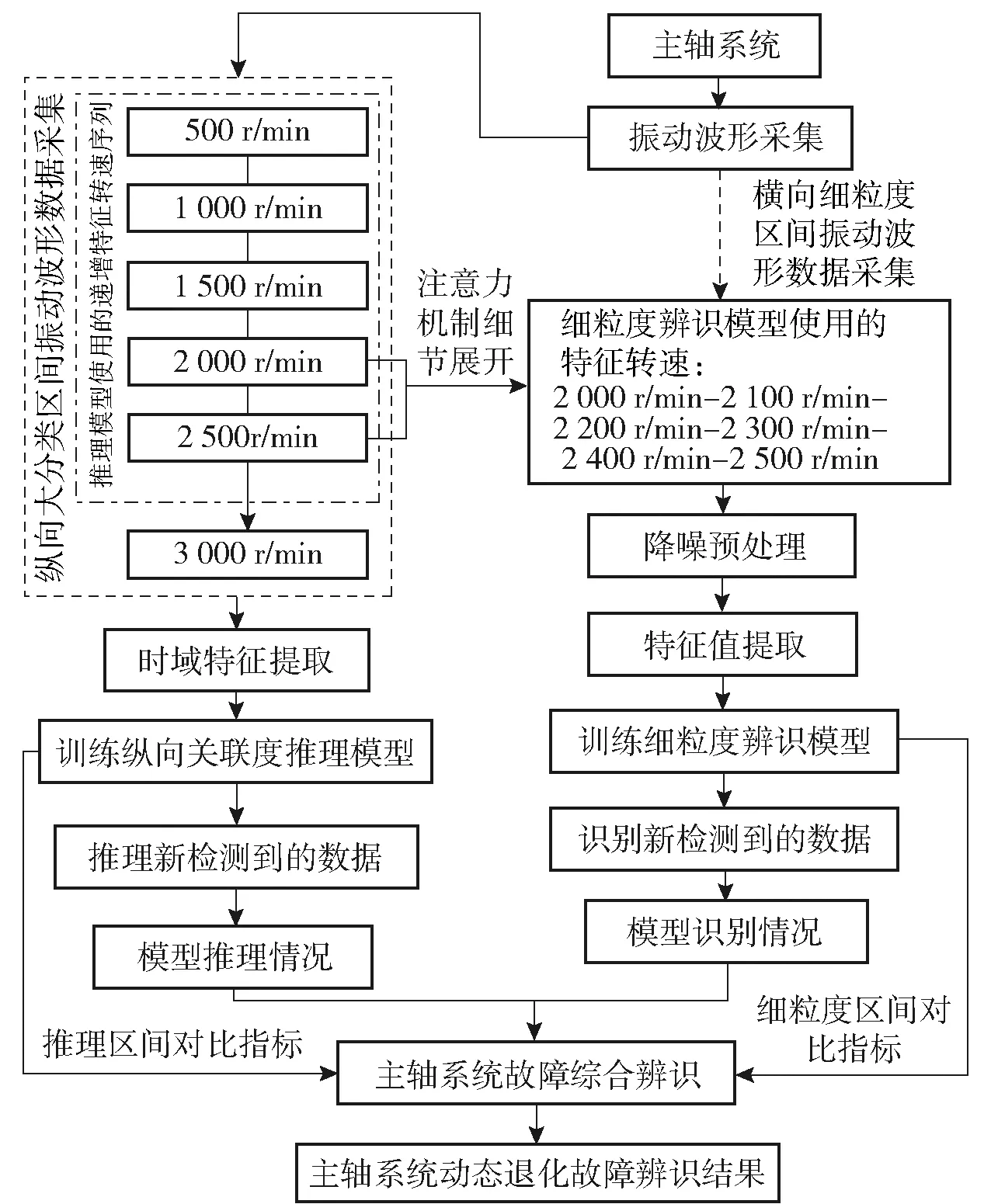
图2 注意力机制算法研究框架Fig.2 Research framework of attention mechanism algorithm
3)划分全局大分类与局部细粒度区间的目的。基于1.2节主轴系统区别于普通回转类机械结构的典型故障特征,本文进行全局大分类与局部细粒度两类区间划分的目的如下:
研究维度方面:全局大分类区间的诊断在于从整体变化趋势角度进行类间记忆递推以发现故障,对于低维度数据在模型时间展开步数低的情况下,运行效率较高。局部细粒度分析在于从保障设备最关键区间精度的角度诊断故障,采用高维度数据及复杂模型区分细节特征优势明显,但运行效率较低。如果对设备整体上全部进行细粒度分析,会产生大量非关键退化故障状态的冗余诊断。而仅使用全局大分类区间、不使用细粒度区间,则不利于辨识故障对重点关注的功能区段的具体影响程度。
研究方法方面:循环神经网络,具备记忆与特征推理能力,应用它的目的是挖掘按照一定间隔递增数据序列的前后记忆递推特征变化,但在区分数据序列因类间差异过小而产生的记忆递推特性不明显的细微差异数据辨识方面不具备优势。基于细节差异比较的卷积神经网络,具备良好的细节辨识能力,特别是通过优化模型结构和增加模型训练深度,能最大限度地区分细微特征,但在探究记忆递推数据序列整体特征变化趋势方面不具备优势。
因此,从整体故障相关性变化趋势及细节辨识的角度,本文划分了全局大分类区间与局部细粒度区间两个维度,并依各区间特点匹配深度学习算法。
2.2 多种波形数据的选取
根据同一机床的主轴系统在同一条件下连续特征转速的内在关联性强的特点,采用振动传感器检测主轴系统在特征转速段所产生的振动数据作为研究数据。以转速500 r/min为递增量,测试常用转速段的主轴系统振动波形,形成大分类推理研究区间。根据对应机床的加工特性,分析其在实际使用中对精车加工纹理要求较高的重点、敏感区间,以转速100 r/min为递增量,确定细粒度辨识研究区间(见图2)。
2.3 特征值选取
为更好保留波形特征,对大分类区间直接在时域内提取波形的最大值、峰- 峰值、绝对值的平均值、方差、标准差、峭度、均方根、波形因子、峰值因子、脉冲因子、均方差、裕度因子,共12项时域特征。对于细粒度区间,采用自适应软阈值降噪,再进行离散小波包变换,获取特征系数矩阵。
离散小波包变换是具有理论依据的多分辨率波形特征提取算法,它可基于小波包变换的高、低通分解特性,将给定波形数据段所含信息,以小波包变换后所得到的特征系数形式提取出来。将小波包变换后第4层(=4)的16个子频带4,(=0,1,…,15)各自的数据分别作为1行,可以构成小波包特征系数矩阵,如(1)式所示。
=[…]
(1)
2.4 本文深度学习算法模型
2.4.1 全局大分类区间算法模型
门控循环单元(GRU)模型是深度学习循环神经网络的一种,它将长短时记忆(LSTM)模型的忘记门以及输入门进行合成,产生了一个更新门。与LSTM模型相比,GRU模型单元更简单,效果更优,其训练参数量缩减到LSTM模型的2/3,并可有效地抑制过拟合。
如图3所示,本文在充分研究GRU的基础上,对应用于本文全局纵向大分类区间的GRU模型的结构及参数进行反复优化调优,最终采用2个GRU层,分别包含80个GRU和100个GRU,并分别使用舍弃率为20%的舍弃层,构成本文整体GRU模型,经过验证获得了非常好的实际效果。图3中,为当前时刻隐藏层计算出来的输出,为当前时刻的输入,为重置门,为更新门,为激活函数,-1为上一时刻的隐藏层输出,′为当前记忆状态。
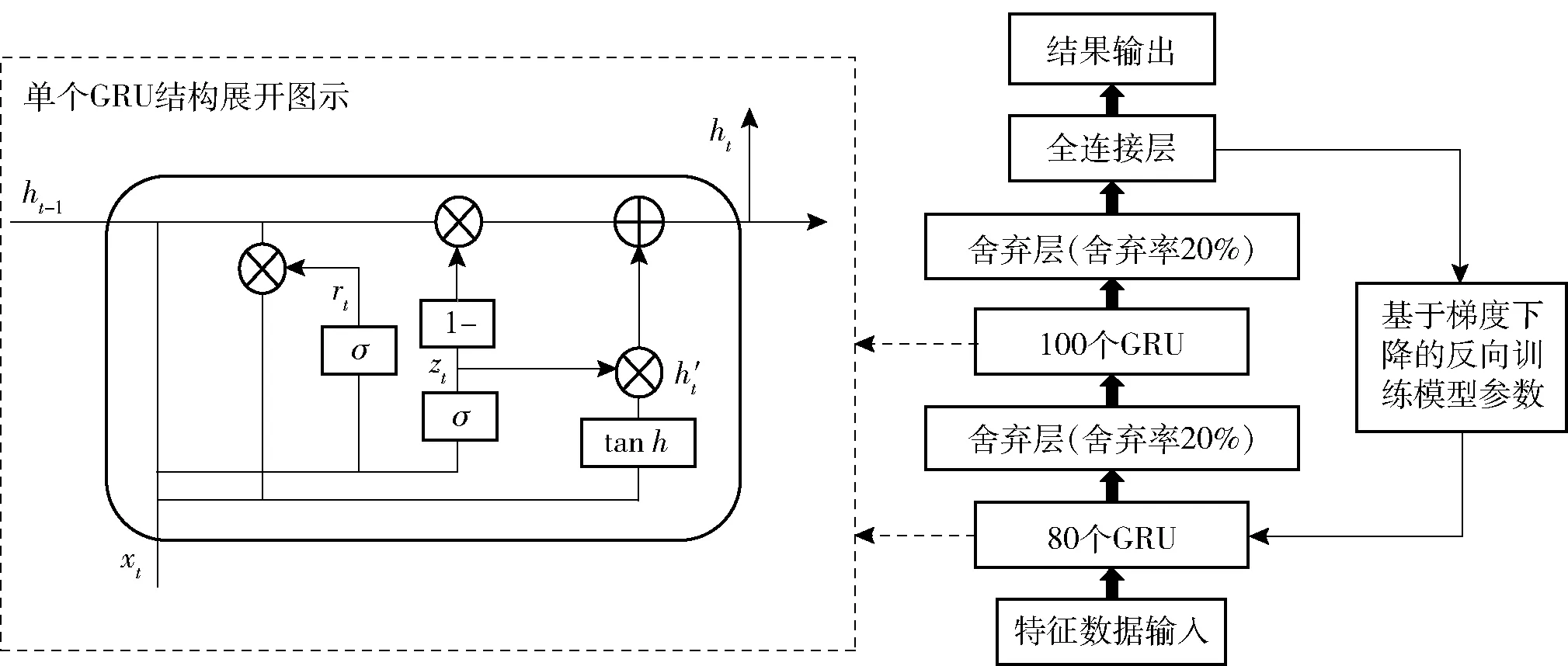
图3 全局大分类区间算法模型(基于GRU模型)Fig.3 Global classification algorithm model (based on GRU model)
2.4.2 局部细粒度区间算法模型
ResNet模型是深度学习算法中卷积神经网络的一种。因其创新的采用残差跳连结构,使其最高可以训练152层深度学习网络,且具有极低的错误率,因此非常适合深度细节差异比较。ResNet18模型是ResNet模型近年来发展出的一种优异的改进架构,包括卷积层和全连接层在内,共含有18个权重层(见图4),其模型感知力、模型识别率较原有网络有大幅提升。
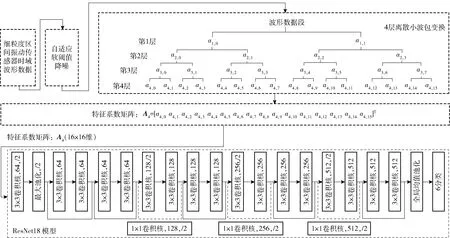
图4 局部细粒度区间算法模型(基于ResNet18模型)Fig.4 Local fine-grained interval algorithm model (based on the ResNet18 model)
如图4所示,根据研究需要,选用ResNet18模型作为细粒度区间故障辨识模型,设计算法流程,优化模型参数,并与Inception等多种卷积神经网络模型对比关于本文问题的解决效果。
3 实验验证及数据分析
为深入分析本文研究方法的机理,验证其有效性、优越性与解决实际问题的能力,下面围绕实际机床装备展开实验验证与数据分析。
徐浡君的风景油画的创作思想,深度建立在荒野哲学的基础之上。所谓荒野哲学,就是以其对生命和自然的深刻体悟、对美丽荒野的细致描绘、对家园毁损和生存危机的忧患意识、对现代生活观念的历史性反思,也被誉为“绿色哲学”。正是荒野哲学在一定意义上改变着整个人类的思想观念和生活方式,它在伦理学与自然、自然中的价值、实践中的环境哲学,以及体验中的自然等诸多方面,渗透出人与自然、人与环境、人与生态的全方位思考,对极端的人类中心主义无限掠夺自然的错误行径,予以深刻的叩问与批判,这就是徐浡君风景油画的哲学意蕴与文化学内涵。
3.1 实验装置及测试的数据
3.1.1 实验对象装置
以一台机床行业内常规普及类4050规格的标准卧式数控车床主轴系统为实验验证对象(见图5(a)、图5(b)、图5(c))。该机床的主轴转速范围0~4 000 r/min。

图5 实验装置Fig.5 Experimental device
1)该机床转速500~3 000 r/min为常用加工转速区间,对应所提算法的全局大分类研究区间。
2)该机床转速2 000~2 500 r/min为主要精加工转速区间,对应所提算法的局部细粒度研究区间。
3)该实验机床主轴系统(见图5(b)、见图5(c))各构成组件的名称描述与本文图1所示的标注相同。
3.1.2 实验检测装置
如图5((a)、图5(d)、图5(e))所示,实验检测装置采用丹麦B&K公司生产的B&K数据采集分析仪、PULSE采集分析软件及振动加速度传感器,具体型号如表1所示。振动加速度传感器1安装于主轴系统前部(见图5(d)),用于采集本文算法研究所需的主轴各转速对应的振动加速度数据。

表1 实验检测装置
3.1.3 实验方法与测试的数据
1)根据图2的算法架构,以该机床装备实际运行的多段目标转速振动检测数据为分析对象,研究验证本文算法的特点。本文主要研究主轴系统侧的1号传感器数据,滑板侧2号传感器作为辅助研究,测试方式同1号传感器(见图5(c))。
2)对于检测获得的各特征转速对应的振动加速度数据,通过B&K数据采集分析软件存储为多组独立的.txt文件,再批量读出文件,在数据分析电脑(台式机CPU i7-9700K;显卡RTX2070;内存32 GB)上按照本文算法进行运算分析验证。
3)测试数据如表2所示。

表2 测试数据
3.2 数据预处理研究
针对细粒度区间的特点,对比基于sym8、coif3、db2、haar小波基自适应软阈值的数据降噪效果(见图6、表3)。最终选出效果最好的sym8小波基进行降噪重构,完成对采集数据的预处理。同样,通过研究2、3、4层离散小波包变换分解特点,选出效果最好的基于db3小波基的4层离散小波包分解系数构成细粒度区间16×16特征值矩阵。
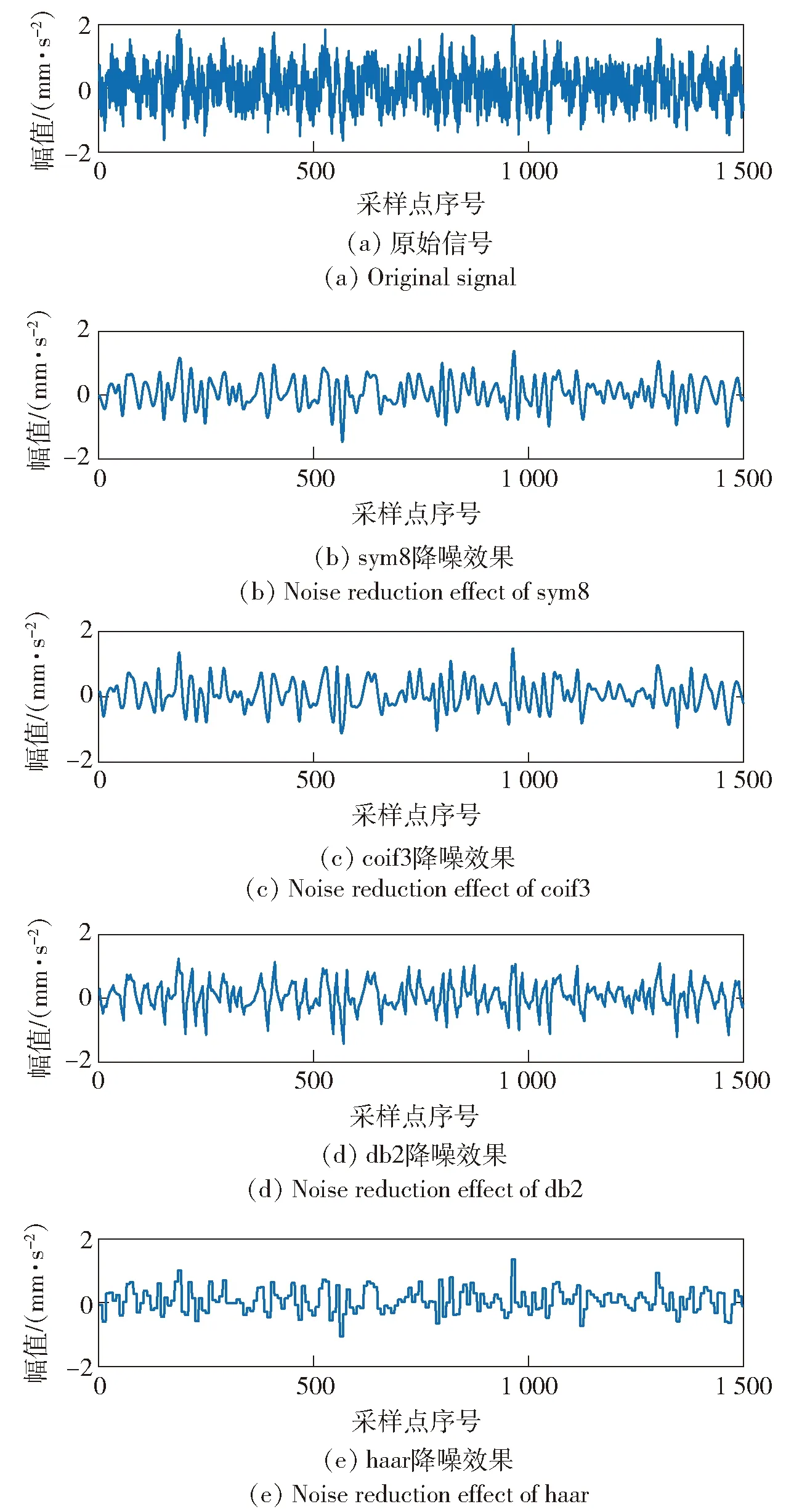
图6 原始信号与多种小波基降噪效果的对比Fig.6 Comparison between original signal and multiple wavelet basis noise reduction

表3 不同小波基降噪效果
3.3 基于GRU的数据分析研究与算法优势对比
本文对全局大分类区间研究采用的方法是基于大分类区间内机床正常状态时采集的500 r/min、1 000 r/min、1 500 r/min、2 000 r/min、2 500 r/min、3 000 r/min连续多段特征转速对应的振动数据特征值,训练模型达到模型稳定。此时使用模型由转速 500~2 500 r/min推理出的转速3 000 r/min与实际转速3 000 r/min的特征数据平均绝对误差等于某一数值。在此后的定期故障推理辨识研究中,针对该机床获得新的大分类区间波形特征数据集,如果在此已经训练好大分类推理模型上的推理辨识结果突然变低,即准故障集模型的推理平均绝对误差明显低于该机床同样测试条件下的正常状态时的模型原验证集的对应数值,即认为出现动态振动状态改变,出现全局大分类区间的故障退化倾向。这里对于12项时域波形特征数据采用每一项数据单独训练比较的方式。
图7、图8所示为针对大分类区间波形标准差特征数据的推理效果对比,其他类同(数据见3.1.3节)。从图7、图8中可以发现,在同样训练参数和输入同样特征数据的情况下,GRU模型推理的转速3 000 r/min 波形特征数据与实际转速3 000 r/min波形特征数据的一致性效果非常好,即模型运行的平均绝对误差较小(达到0.028 7),远优于普通RNN模型(见表4),验证了本文使用GRU模型推理波形特征数据方法的合理性和优越性。
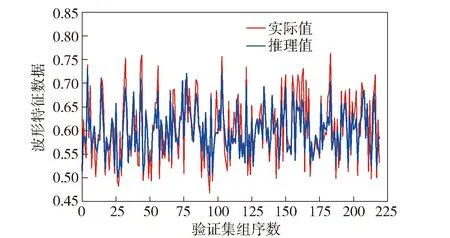
图7 基于GRU模型推理3 000 r/min波形特征数据的效果Fig.7 Effect of reasoning 3 000 r/min waveform feature data based on GRU model

图8 基于RNN模型推理3 000 r/min波形特征数据的效果Fig.8 Effect of reasoning 3 000 r/min waveform feature data based on RNN model
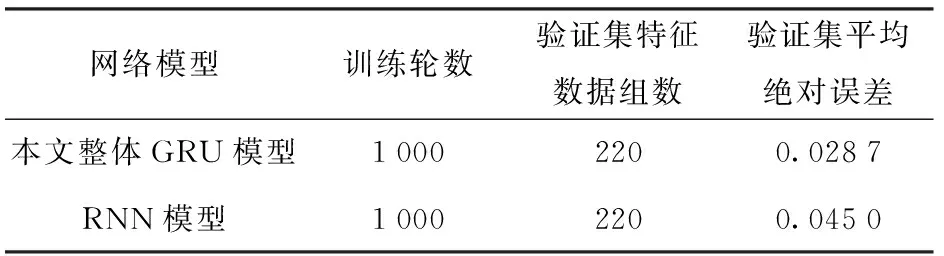
表4 GRU模型与RNN模型对比
3.4 基于ResNet18模型的研究与算法优势对比
本文对局部细粒度区间的研究,是基于小波包特征提取和ResNet18模型的良好识别能力,细分识别2 000 r/min、2 100 r/min、2 200 r/min、2 300 r/min、2 400 r/min、2 500 r/min转速下振动特征数据的类内差异变化特点,训练模型,其原理是对该机床在同样动态条件下训练好模型。在以后定期故障辨识时,针对该机床在细粒度区间获得的准故障波形特征数据集,如果在此已经训练好的细粒度辨识模型上的识别准确率结果突然变低,即明显低于该机床在同样测试条件下原来正常状态训练模型时的验证集(与训练集同步划分)的辨识准确率,即认为出现动态振动状态改变,出现局部细粒度区间故障。
为验证ResNet18模型的优越性和合理性,基于3.1.3节特征数据,进行其与Inception、基本卷积神经网络(BConvNet)、LeNet、VGG模型的准确率和损失率辨识效果对比,结果如图9~图13及表5所示。

图9 基于ResNet18模型的识别效果Fig.9 Identification effect based on ResNet18 model
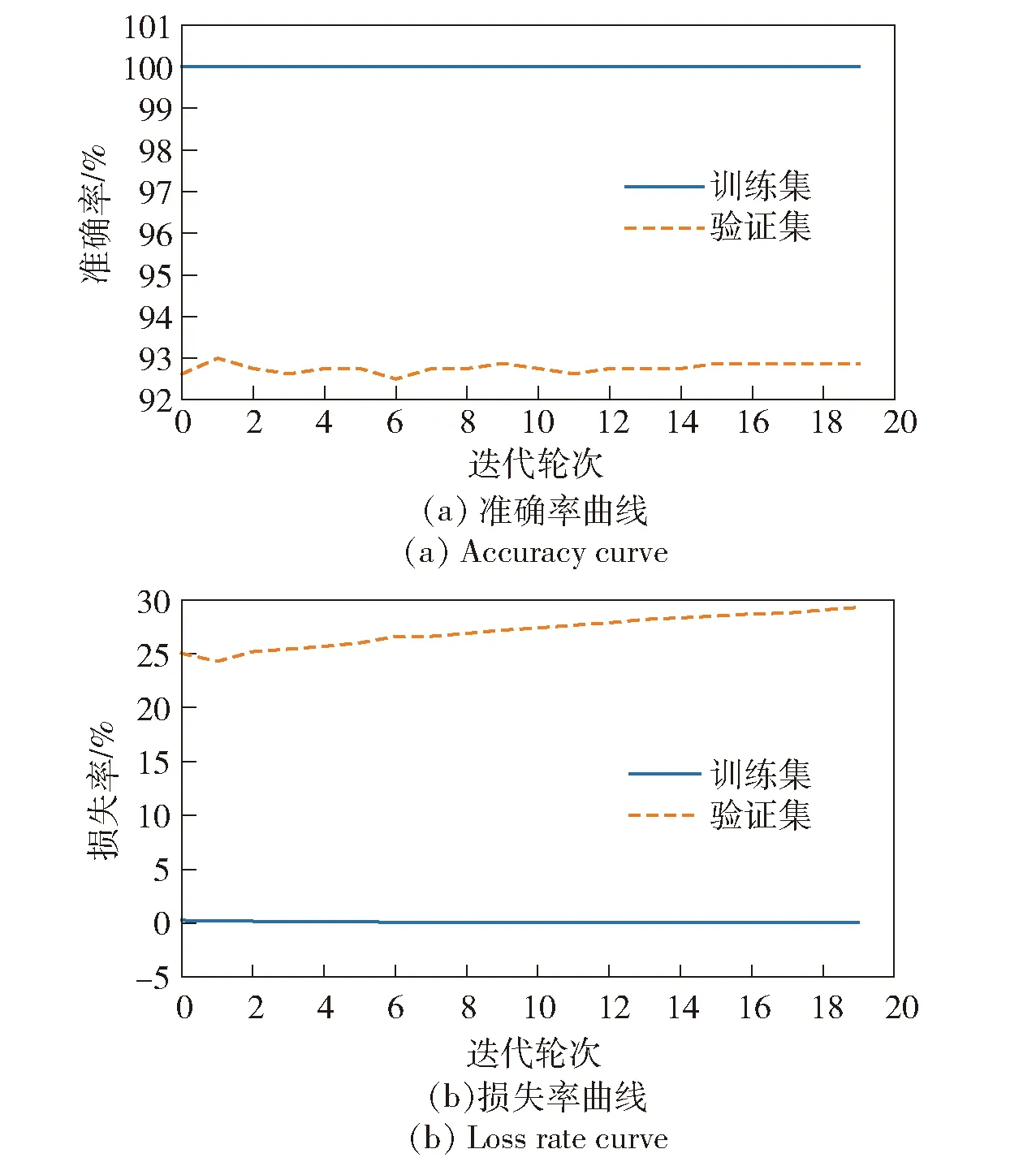
图10 基于Inception模型的识别效果Fig.10 Identification effect based on Inception model

图11 基于BConvNet模型的识别效果Fig.11 Identification effect based on BConvNet model

图12 基于LeNet模型的识别效果Fig.12 Identification effect based on LeNet model
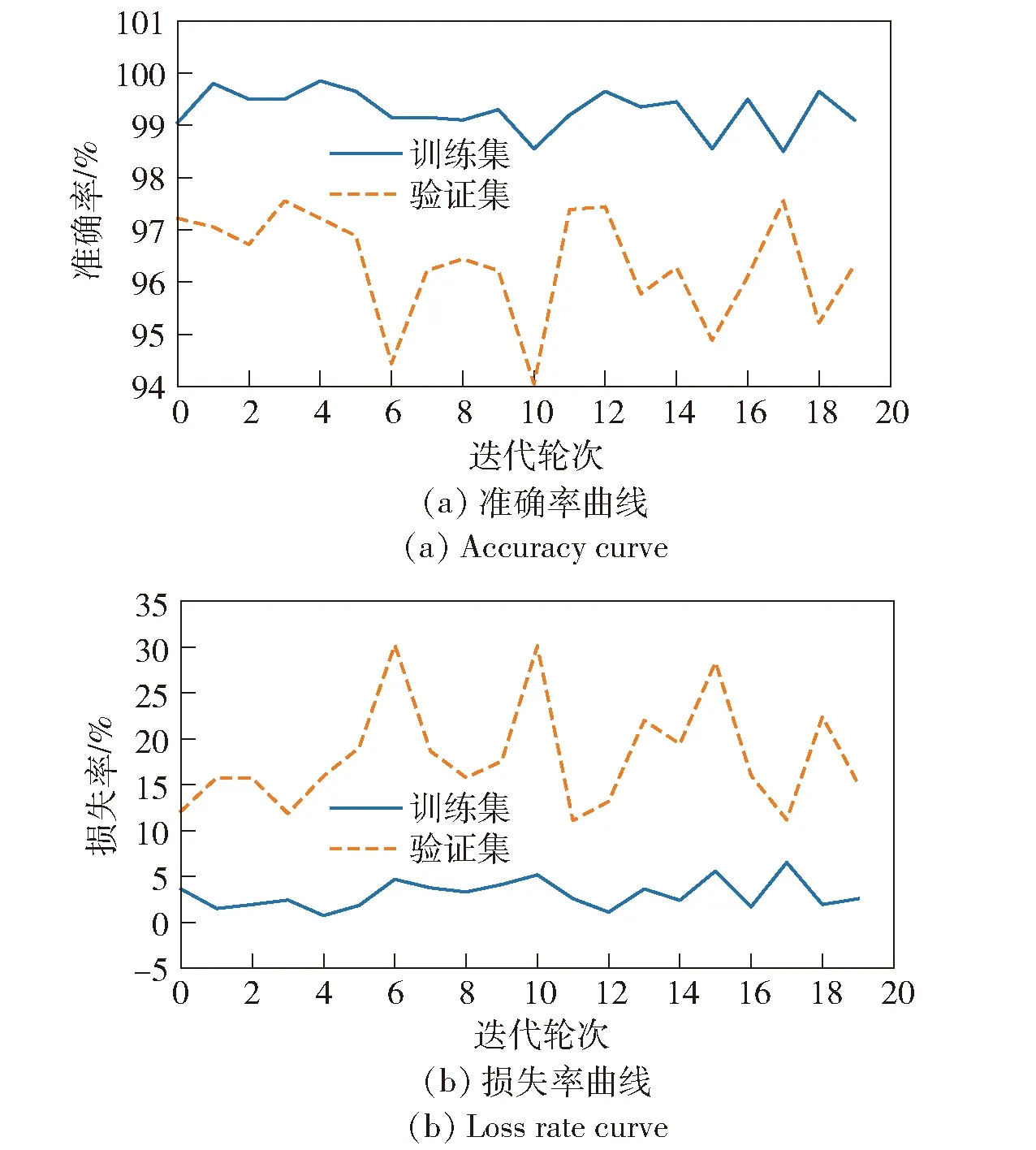
图13 基于VGG模型的识别效果Fig.13 Identification effect based on VGG model
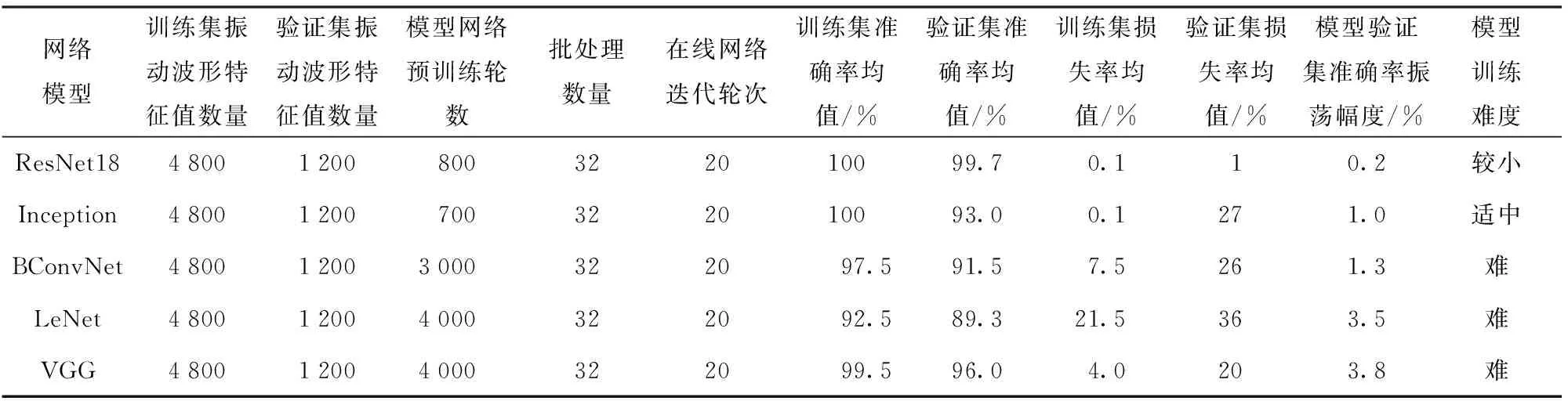
表5 ResNet18模型与其他模型数据对比
从图9~图13及表5中发现:ResNet18模型对验证集的辨识准确率达99.7%,损失率仅为1%,均优于其他模型;其模型验证集准确率数值分布振荡幅值相比最小,表明其泛化能力更好,鲁棒性更强;其预训练轮数较少,训练难度较小(预训练的目的是获得稳定的网络结构)。
4 实际故障验证
为有效验证本文模型及方法对于实际故障的分析解决能力,基于FMECA思想,即故障模式、影响和危害性分析,进行基于实际故障数据的主轴系统空载、负载状态下的故障辨识研究。
4.1 对主轴系统平行不对中典型实际故障的空载验证
机床在实际使用中,按照故障产生方向,主轴系统故障可分为径向故障和轴向故障。其中,主轴系统平行不对中故障(见图14,图中Δ为不对中偏差量),是一类典型且常见的径向故障。故障原因为主轴连接组件不同轴。故障损害为造成油缸、拉杆、卡盘不同心,产生主轴系统异常振动,影响加工。根据该台机床(3.1节中的研究对象机床)在一段时间实际使用中出现的带有主轴系统径向不对中故障时的检测数据,按照与3.1.3节中对应数据集相同的方式提取出故障集进行相应模型算法的空载故障辨识。图15所示为主轴系统在无故障情况下2 100 r/min转速时波形,图16所示为主轴系统在含有不对中故障情况下2 100 r/min转速时波形。

图14 平行不对中Fig.14 Parallel misalignment
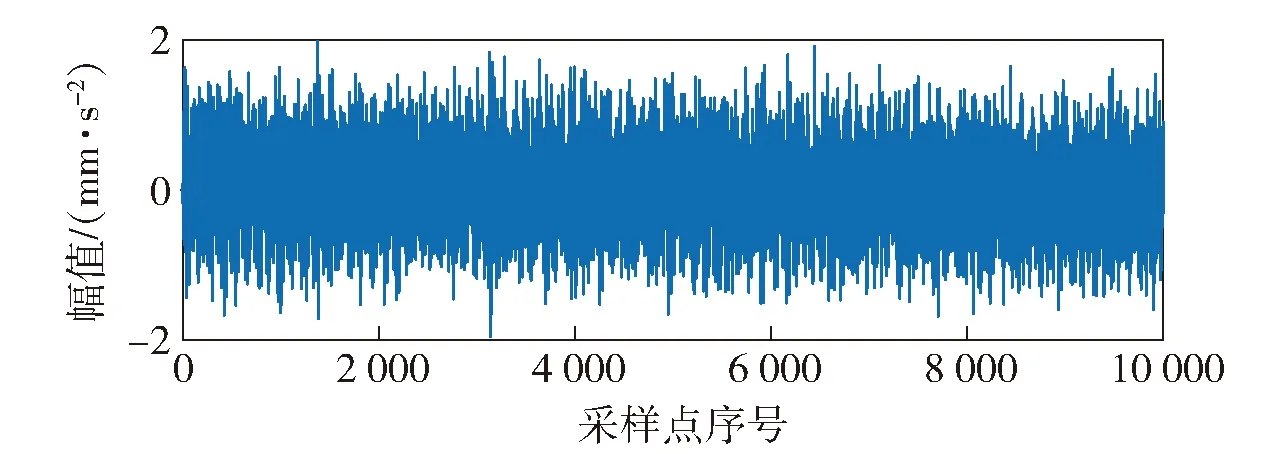
图15 主轴系统在无故障情况下2 100 r/min转速时波形Fig.15 Vibration waveform of spindle system at 2 100 r/min without fault
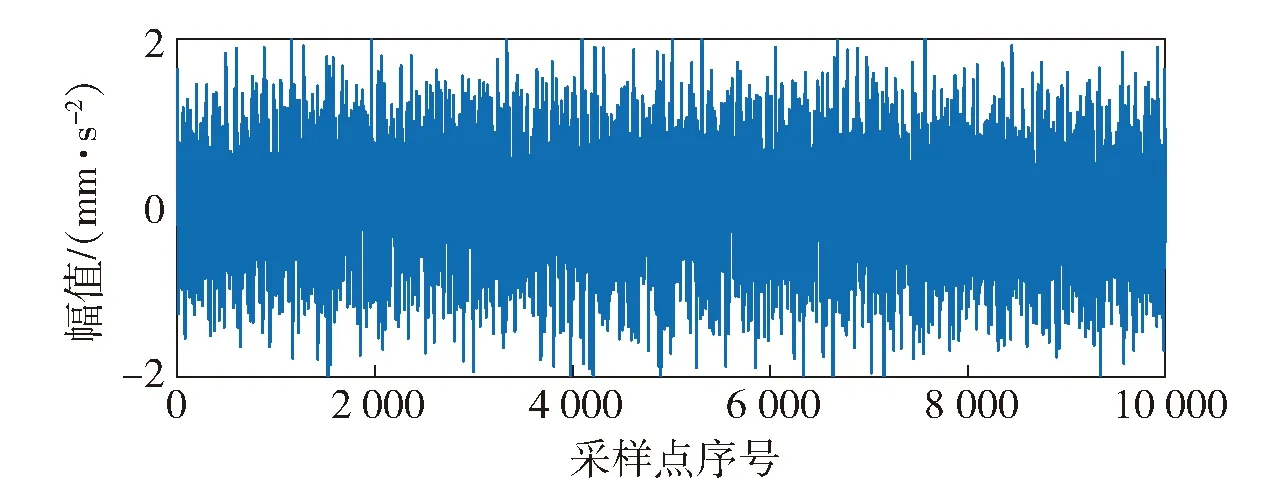
图16 主轴系统在含有不对中故障情况下2 100 r/min转速时的波形Fig.16 Vibration waveform of spindle system with misalignment fault at 2 100 r/min
比较图15、图16可以发现,相同转速下平行不对中故障会带来主轴振动波形幅值变化程度的增加,但仅凭观察者经验较难准确量化辨识。为验证本文大分类推理模型算法对于不对中故障的推理辨识能力,使用本文算法中的调优后GRU模型对该故障进行辨识研究。大分类区间正常波形的GRU模型推理效果如图17所示。
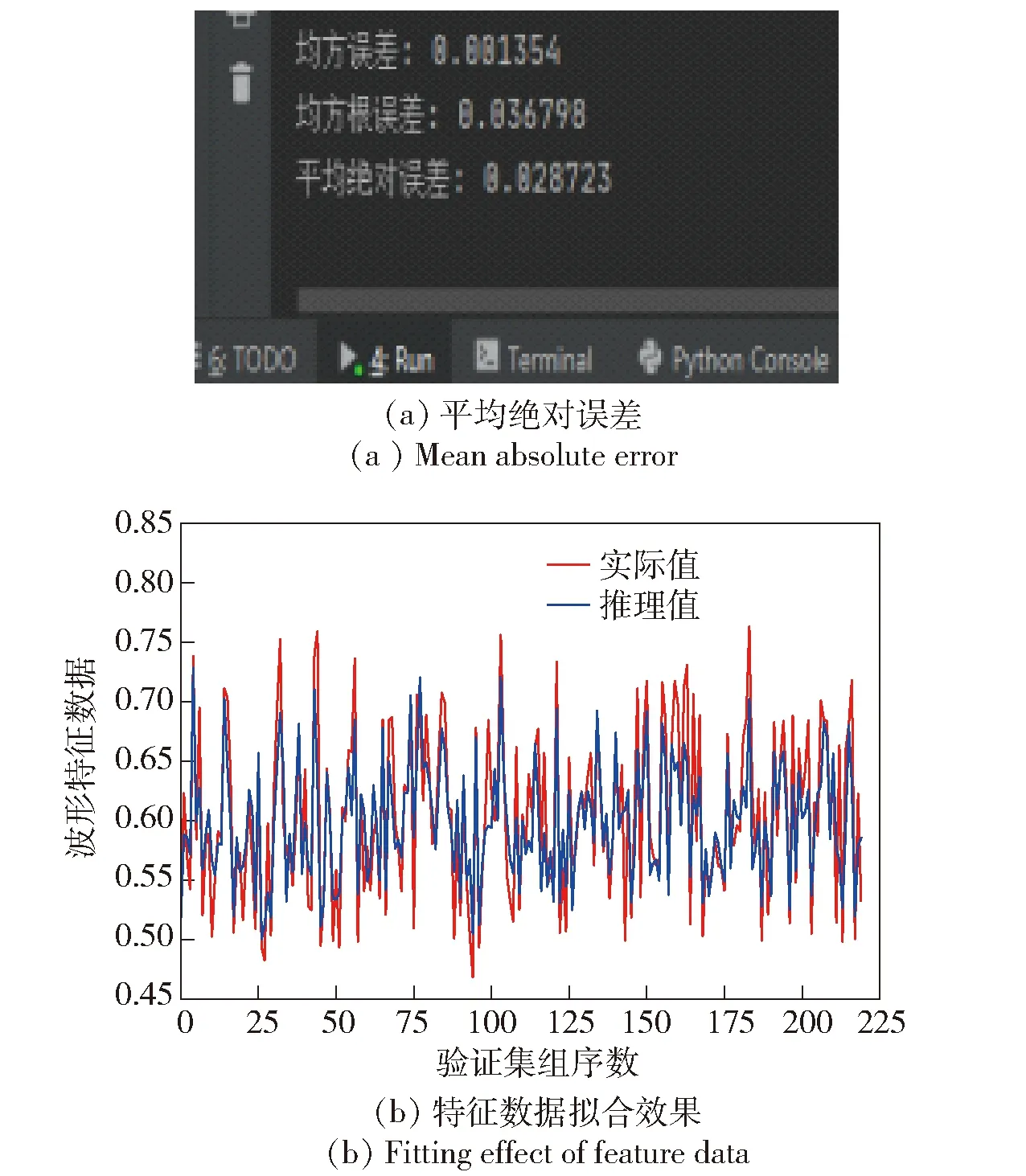
图17 大分类区间正常波形的GRU模型推理效果Fig.17 GRU model reasoning effect of normal waveform in large classification interval
大分类区间含不对中故障波形的GRU模型推理效果如图18所示。
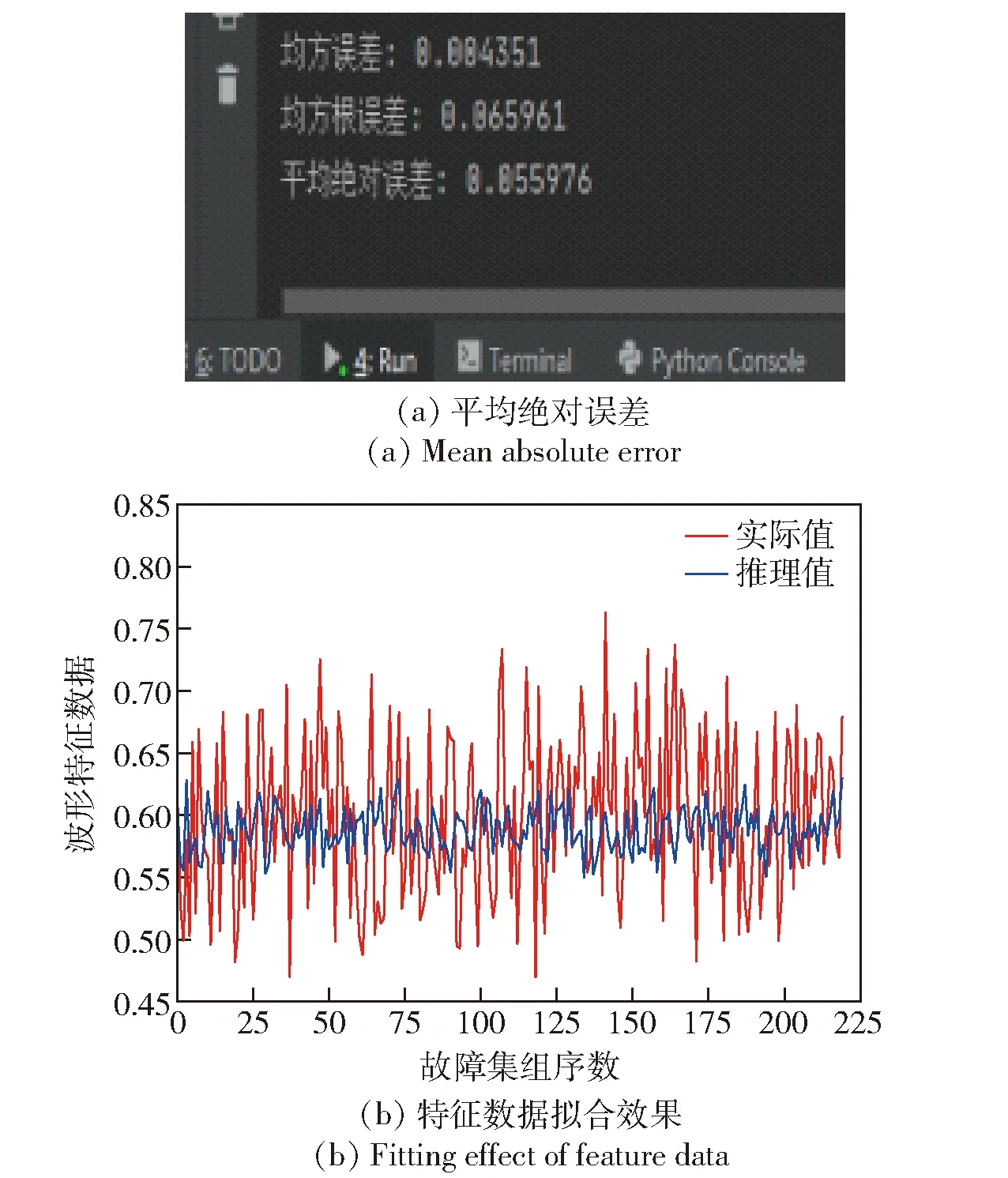
图18 大分类区间含不对中故障波形的GRU模型推理效果Fig.18 GRU model reasoning effect of waveform with a symmetric fault in large classification interval
为验证本文提出的局部细粒度辨识模型算法对于平行不对中故障的辨识能力,采用已训练好的ResNet18模型,在3.1.3节的数据获取条件下,对于出现的该故障进行空载辨识,结果如图19所示。
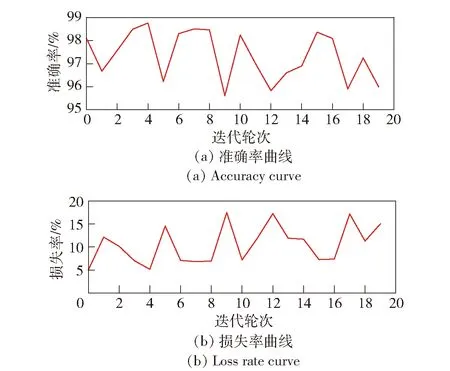
图19 细粒度区间ResNet18模型对出现不对中故障的辨识Fig.19 Identification of faults in ResNet18 model with fine-grained interval
4.2 对主轴系统某转速段共振典型故障的空载验证
共振故障是对机电系统特别是回转类主轴系统影响较大的一类故障,一般出现在个别转速区间。故障状态为机床装配后或长期使用中出现个别转速区间的主轴系统共振,故障损害为造成加工振纹、损伤刀具、加速主轴系统退化。产生的原因有主轴系统连接件松动、连接件外形损伤、固有频率改变、机床地脚松动等。根据该台机床(3.1节中的对象机床)在不同时期实际使用中检测到的在2 000 r/min转速时出现的共振,以及随着主轴结构件损伤加剧,在一段时间后在2 000 r/min、2 500 r/min转速时同时出现共振两种情况的故障数据,按3.1.3节方式提取故障集进行相应模型算法的空载辨识。
验证GRU模型对2 000 r/min及2 000 r/min、2 500 r/min 转速都出现共振故障的模型推理辨识能力,结果如图20、图21所示。

图20 大分类区间2 000 r/min转速时含共振故障的波形的GRU模型推理效果Fig.20 GRU model reasoning effect of waveform with resonance fault in large classification at 2 000 r/min
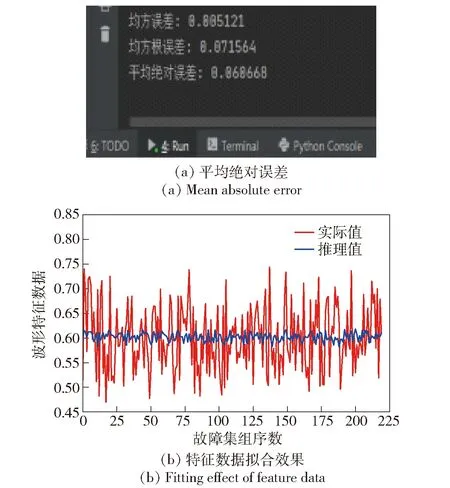
图21 大分类区间2 000 r/min和2 500 r/min转速都含共振故障的波形的GRU模型推理效果Fig.21 GRU model reasoning effects of waveform with resonance fault in large classification at 2 000 r/min and 2 500 r/min
验证ResNet18模型对2 000 r/min及2 000 r/min、2 500 r/min 转速都出现共振故障的辨识,结果如图22、图23所示。

图22 细粒度区间ResNet18模型对2 000 r/min转速下出现共振故障的辨识Fig.22 Identification of resonance at 2 000 r/min by ResNet18 model of fine-grained interval
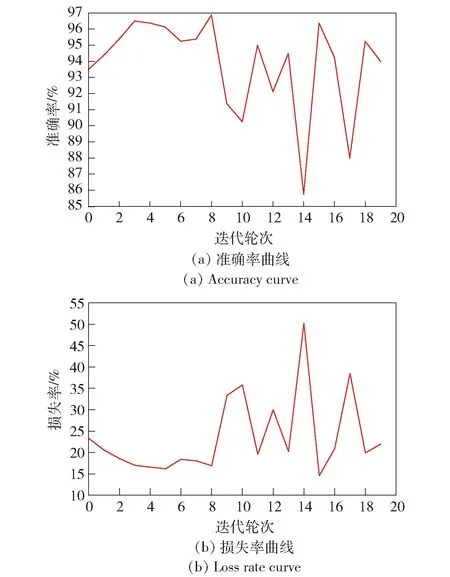
图23 细粒度区间ResNet18模型对2 000 r/min和2 500 r/min转速下都出现共振故障的辨识Fig.23 Identification of resonance faults at 2 000 r/min and 2 500 r/min by ResNet18 model of fine-grained interval
4.3 空载故障辨识综合分析及注意力机制结果分析
表6所示为空载状态下故障辨识效果对比。根据表6对4.1节、4.2节结果数据的汇总,可从相关数据上印证本文两类区间研究的各自算法有效性与准确性。同时,在应用大分类区间进行“粗健康体检”时发现,共振故障时GRU推理模型对转速 2 000 r/min 单一状态与转速2 000 r/min、2 500 r/min两种状态同时出现共振故障的问题,推理结果差别不大,数据增长梯度仅为6.6%,如果细分故障,就要针对重点关键转速区间进行展开研究,应用注意力机制进行细粒度横向细节辨识。随后ResNet18细粒度辨识模型的研究结果验证了细粒度研究的必要性和故障区分的准确性,相关结果数据增长梯度为43.8%。由6.6%到43.8%的变化增加了对单一共振故障与两项共振故障辨识时的类间区分度。以上结果验证了针对复杂非线性多组件耦合的机床主轴系统,使用本文提出的基于注意力机制和深度学习算法进行研究的必要性和重要实际意义。
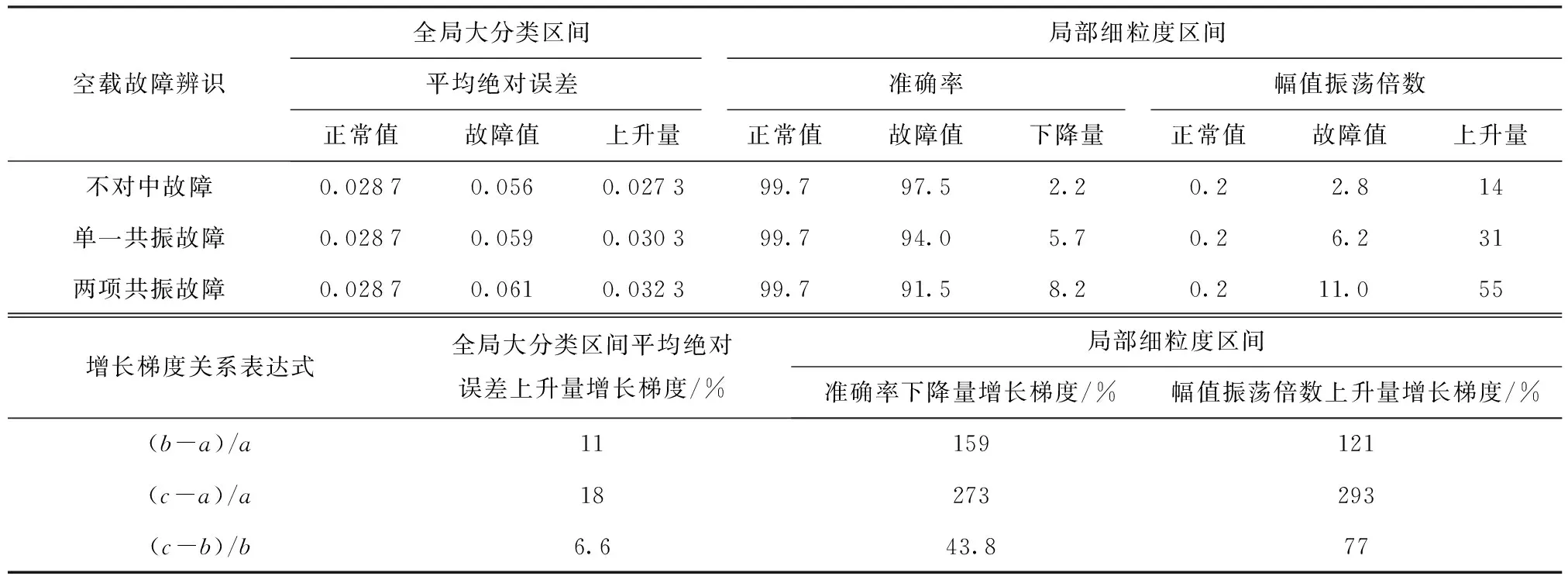
表6 空载状态下故障辨识效果对比
4.4 对于主轴系统在负载加工状态下的故障辨识验证
为进一步验证所提模型算法的适应性,下面研究注意力机制及其算法模型对主轴系统在负载加工时的故障辨识效果。
采取在该型号正常机床、故障机床上各精车加工一批同样尺寸零件的方案(见图24),创造一致的负载加工条件。选取该机床在卡盘油缸连接盘出现径向窜动偏心时所产生的主轴系统不同轴故障作为机床故障状态。同时,为最大限度地减少切削条件等因素的影响,在切削过程中严格控制切削参数及切削条件,如表7所示。

图24 主轴系统负载加工Fig.24 Load processing of spindle system
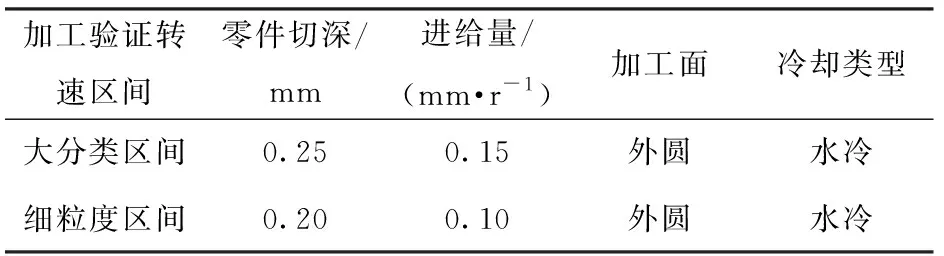
表7 加工参数及条件
数据获取方式如下:采集在各加工验证转速区间内,零件切削中平稳状态时主轴系统的振动传感器数据,经过滤波去噪处理,获得稳定的波形数据。根据切削状态下振动波形数据具备的高频特征,除进行与2.3节空载研究相同的时域特征数据提取外,还增加了通过快速傅里叶变换频谱分析方法获得频域特征数据,包括频谱幅值平均值、频谱幅值标准方差特征数据。应用2.4节全局大分类区间的整体GRU模型(对应特征数据为频谱幅值平均值)和局部细粒度区间ResNet18模型(对应特征数据为时域波形小波包变换分解系数矩阵)进行运算验证,结果如图25~图28所示,汇总模型运算结果如表8所示。
从图25~图28及表8中发现,本文模型对于负载加工复杂状态下的机床故障状态具有很好的辨识效果,进一步验证了本文算法的有效性及实际意义。
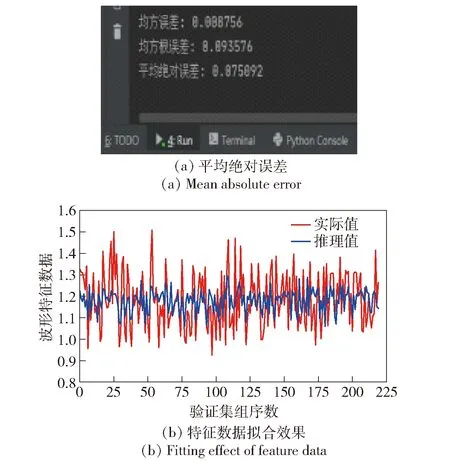
图25 负载加工状态大分类区间正常时GRU模型推理效果Fig.25 Reasoning effect of GRU model under the condition of large classification interval in processing state
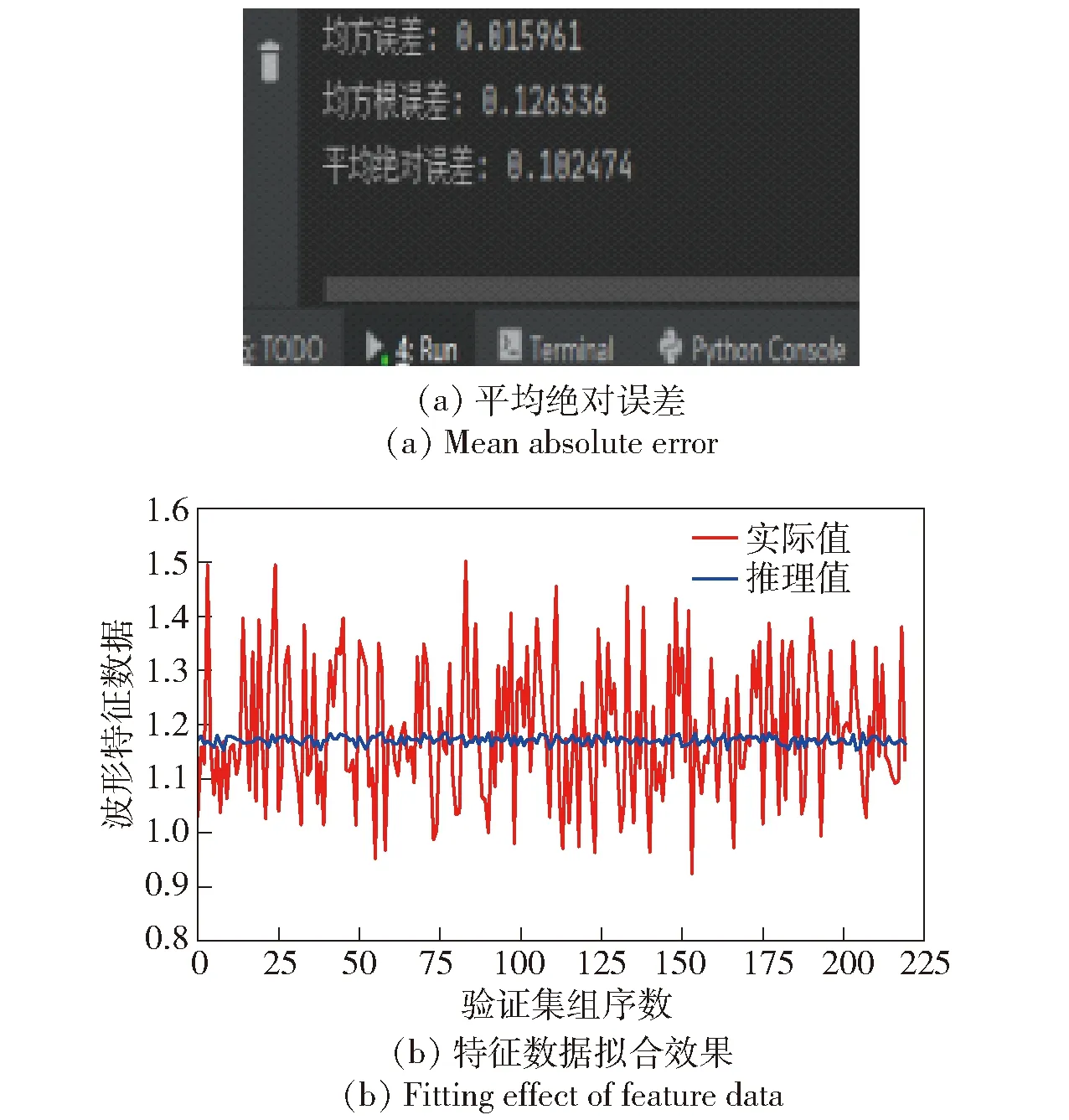
图26 负载加工态大分类区间不同轴故障时GRU模型推理效果Fig.26 GRU model reasoning effect of axial misalignment faults in large classification interval in load processing state
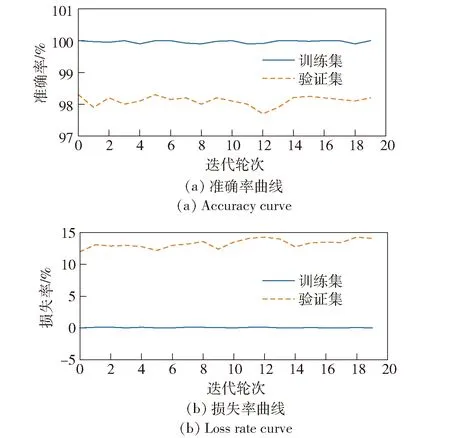
图27 负载加工状态细粒度区间正常时ResNet18模型辨识效果Fig.27 ResNet18 model identification effect in normal fine-grained interval of load processing state

图28 负载加工态细粒度区间不同轴故障时ResNet18模型辨识效果Fig.28 ResNet18 model identification effect of axial misalignment faults in fine-grained interval of load processing state

表8 负载加工状态下故障辨识效果对比
5 结论
本文设计了解决实际机床主轴系统整体故障辨识问题的注意力机制研究架构,实现了基于GRU模型的纵向全局渐变故障趋势记忆递推辨识和基于ResNet18模型的横向局部细粒度细节辨识两个相互关联维度的有机结合。得到主要结论如下:
1)使用sym8小波基的自适应软阈值降噪,可有效滤除干扰,利于提高模型的辨识能力。
2)提出的GRU模型对大分类区间数据特征的记忆推理辨识能力优于RNN模型。ResNet18模型的细节数据特征差异辨识能力、鲁棒性均优于Inception、BConvNet、LeNet、VGG模型。
3)通过平行不对中、共振等实际典型故障,验证了本文所提方法在空载条件下的有效性和准确性。通过对实际负载加工态故障辨识的研究,进一步验证了所提模型的辨识能力及研究的实际意义。
4)提出的注意力机制优势明显,满足了主轴系统故障辨识的高效性和准确性(推理模型“粗健康体检”体现了高效性,细粒度研究体现了聚焦故障的准确性),为相关问题研究提供了借鉴。

