最优切割问题研究

王奕为

摘 要：该文主要研究了在给定条件下如何对二维矩形木板的最优切割问题，重点研究分析了在完成要求的生产任务和木板利用率最高的前提下单一产品和多个产品的最优切割方案，在此基础上进一步讨论了不同要求下总利润最大的木板切割方案，并通过建立相关数学模型进行求解，计算结果表明建立的数学模型有效可靠且寻优能力较好，能够有效解决木板最优切割问题。

关键词：最优切割  原材料利用率  产品利润率  枚举法

中图分类号：TS652    文献标识码：A文章编号：1672-3791（2022）03（b）-0000-00

Study on the Optimal Cutting Problem

WANG Yiwei

（Yancheng Polytecnic College， Yancheng， Jiangsu Province， 224005 China）

Abstract： This paper mainly studies the optimal cutting problem of wood under given conditions， the optimal cutting schemes of single product and multi-product are studied and analyzed under the demand of required production tasks and the highest utilization rate of wood board. On this basis， the cutting scheme with the maximum total profit under different requirements is further discussed and solved by establishing relevant mathematical models. The numerical results show that the mathematical model is effective， reliable and has a good searching ability， the new model can effectively solve the problem of the optimal cutting of wood.

Key Words： Optimal Cutting; Raw material utilization; Product profit margin; Enumeration method

1 问题描述

“木板最优切割问题 ”是把相同形状的一些原材料分割加工成若干个不向规格大小的零件的问题，此类问题在工程技术和工业生产中有着重要和广泛的应用.工厂中经常会碰到一些材料切割的优化问题，为了节省材料，减少废料对环境的污染，必须选择最优的切割方案，实际上也是一类特殊的布局排样优化问题[1-4]。这里的“木板最优切割问题”主要考虑某企业的实际条件限制下的单一材料切割问题。即在加工过程中，木板被切割成不同形状和面积，分别加工成不同的产品。在木板的面积和数量有限的情况下，安排木板切割使得在完成生产任务的基础上，使木板利用率最大化和企业利润最大化，这是企业亟需解决的问题。简化和优化切割操作，对提高企业的经济效益和增大产品竞争力具有极为重要的意义。

1.1 问题背景

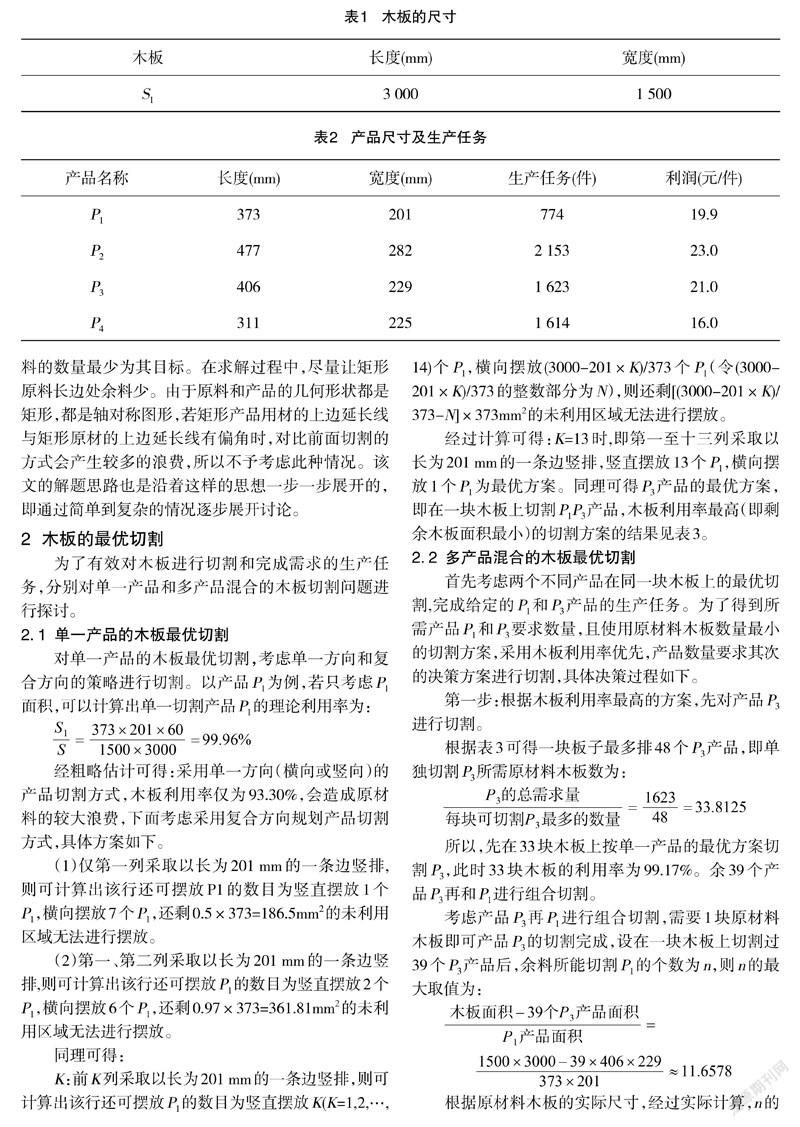
某企业新进一批木板，其相关数据如表1所示，在家具加工的过程中，需要使用切割工具生产产品，其生产的产品相关数据如表2所示，上述内容则为该企业设计木板的最优切割方案。

基本假设如下。

木板厚度和割缝宽度忽略不计。

每次切割都很精确，不会出现意外损耗。

切割產品的长和宽与原材料的长和宽平行。

不考虑切割方式增加所带来的成本增加。

符号说明：

为矩形板材的长边; 为矩形板材的宽边; 为矩形板材的长宽比; 为矩形板材的面积;

Si为第 种产品用材的面积 ;Hi为第 种产品的单位利润（i=1，2，3，4）。

1.2问题分析

论文主要研究的是木板的最优切割问题，此问题实质上是一个下料问题[5-7]，在进行切割时涉及到不同类型产品长和宽同时改变，是两个变量在变，所以在建立模型时以剩余原材料的余量面积最小和使用的原材料的数量最少为其目标。在求解过程中，尽量让矩形原料长边处余料少。由于原料和产品的几何形状都是矩形，都是轴对称图形，若矩形产品用材的上边延长线与矩形原材的上边延长线有偏角时，对比前面切割的方式会产生较多的浪费，所以不予考虑此种情况。该文的解题思路也是沿着这样的思想一步一步展开的，即通过简单到复杂的情况逐步展开讨论。

木板的最优切割

为了有效对木板进行切割和完成需求的生产任务，分别对单一产品和多产品混合的木板切割问题进行探讨。

单一产品的木板最优切割

对单一产品的木板最优切割，考虑单一方向和复合方向的策略进行切割。以产品P1为例，若只考虑P1面积，可以计算出单一切割产品P1的理论利用率为：

S_1/S=（373×201×60）/（1500×3000）=99.96%

经粗略估计可得：采用单一方向（横向或竖向）的产品切割方式，木板利用率仅为93.30%，会造成原材料的较大浪费，下面考虑采用复合方向规划产品切割方式，具体方案如下。

（1）仅第一列采取以长为201 mm的一条边竖排，则可计算出该行还可摆放P1的数目为竖直摆放1个P1，横向摆放7个P1，还剩0.5×373=186.5mm2的未利用区域无法进行摆放。

（2）第一、第二列采取以长为201mm的一条边竖排，则可计算出该行还可摆放P1的数目为竖直摆放2个P1，横向摆放6个P1，还剩0.97×373=361.81mm2的未利用區域无法进行摆放。

同理可得：

K：前K列采取以长为201 mm的一条边竖排，则可计算出该行还可摆放P1的数目为竖直摆放K （K=1，2，…，14）个P1，横向摆放（3000-201×K）/373个P1（令（3000-201×K）/373的整数部分为N），则还剩[（3000-201×K）/373-N]×373mm2的未利用区域无法进行摆放。.

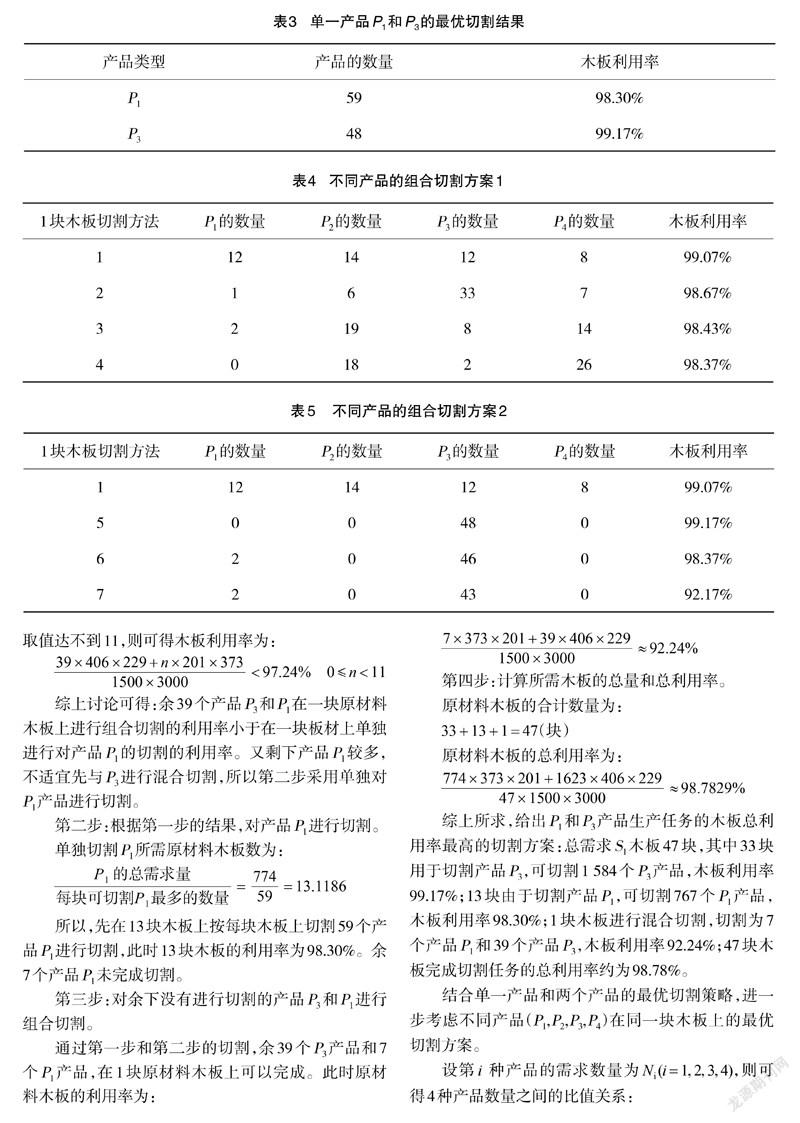
经过计算可得：K=13时，即第一至十三列采取以长为201mm的一条边竖排，竖直摆放13个P1，横向摆放1个P1为最优方案。同理可的P3产品的最优方案，即在一块木板上切割P1 P3产品，木板利用率最高（即剩余木板面积最小）的切割方案的结果见表3。

2.2多产品混合的木板最优切割

首先考虑两个不同产品在同一块木板上的最优切割，完成给定的P1和P3产品的生产任务。为了得到所需产品P1和P3要求数量，且使用原材料木板数量最小的切割方案，采用木板利用率优先，产品数量要求其次的决策方案进行切割，具体决策过程如下。

第一步：根据木板利用率最高的方案，先对产品P3进行切割。

根据表3可得一块板子最多排48个P3产品，即单独切割P3所需原材料木板数为：

（P_3 的总需求量）/（每块可切割P_3 最多的数量）=1623/48=33.8125

所以先在33块木板上按单一产品的最优方案切割P3，此时33块木板的利用率为99.17%。余39个产品P3再和P1进行组合切割。

考虑产品P3再P1进行组合切割，需要1块原材料木板即可产品P3的切割完成，设在一块木板上切割过39个P3产品后，余料所能切割P1的个数为n，则n的最大取值为：

（ 木板面积-39个P_3 产品面积）/（P_1 产品面积）=（1500×3000-39×406×229）/（373×201）≈11.6578

根据原材料木板的实际尺寸，经过实际计算，n的取值达不到11，则可得木板利用率为：

综上讨论可得：余 个产品P3和P1在一块原材料木板上进行组合切割的利用率小于在一块板材上单独进行对产品P1的切割的利用率。又剩下产品P1较多，不适宜先与P3进行混合切割，所以第二步采用单独对P1产品进行切割。

第二步：根据第一步的结果，对产品P1进行切割：

单独切割P1所需原材料木板数为：

（P_1 的总需求量）/（每块可切割P_1 最多的数量）=774/59=13.1186

所以先在13块木板上按每块木板上切割59个产品P1进行切割，此时13块木板的利用率为98.30%。余7个产品P1未完成切割。

第三步：对余下没有进行切割的产品P3和P1进行组合切割。

通过第一步和第二步的切割，余39个P3产品和7个P1产品，在1块原材料木板上可以完成。此时原材料木板的利用率为：

综上所求，给出P1和P3产品生产任务的木板总利用率最高的切割方案：总需求S1木板47块，其中33块用于切割产品P3，可切割1584个P3产品，木板利用率99.17%;13块由于切割产品P1，可切割767个P1产品，木板利用率98.30%;1块木板进行混合切割，切割为7个产品P1和39个产品P3，木板利用率92.24%;47块木板完成切割任务的总利用率约为98.78%。

结合单一产品和两个产品的最优切割策略，进一步考虑不同产品（P1，P2，P3，P4）在同一块木板上的最优切割方案。

设第i 种产品的需求数量为N_i （i=1，2，3，4），则可得四种产品数量之间的比值关系：

即在优选组合方案时，可以按N_1：N_2：N_3：N_4≈1：3：2：2的比例进行考虑选取求解，对于方案确定后进行切割所产生的产品多余或剩余部分再进行单独考虑。按上述方法的思路进行组合求解，可得如下最优组合方案，具体内容见表4和表5。

对方案1，根据要求的具体数量和比例关系，测算可得：为完成所有产品的生产任务，各类切割方法所需要进行切割的木板数为：方法1需要切割51～54块左右：方法2需要切割13～14块左右;方法3需要切割60～63块左右;方法4需要切割8块左右。

设完成任务后，方法1至少需要切割y_1块木板，方法2至少需要切割y_2块木板，方法3至少需要切割y_3块木板，方法4至少需要切割y_4块木板，则有：

按上述方案确定的木板数进行切割，可得：

即P1产品全部切割完成，剩余5个P2产品、13个P3产品、16个P4产品没完成切割。

第二步：对第一步剩余产品完成切割。

根据第一步的结果，剩余5个P2产品、13个P3产品、16个P4产品可以在一块原材料木板上即可切割完成，且木板有剩余。即全部完成4类产品的生产切割任务需138块木板。同理根据方案2的切割方式，全部完成4类产品的生产任务需139块木板。综合可得最优切割方案为方案1。

如果不考虑产品P1，P2，P3，P4的需求数量，给定S1木板的数量（假设木板数量为100块），求解总利润最大的切割方案。根据给出的产品利润，求每种产品的单位利润，按单位利润对产品进行排序，然后结合每块木板切割产品的利用率给出每块木板不同切割的利润，最后给出总利润最大的切割方案。

即四种产品的单位利润率大小顺序为：H_1>H_4>H_3>H_2.先考虑以产品的单位利润高的产品进行切割方案的确定，寻找利润率最高的切割方案。

设每块木板可切割x_i （i=1，2，3，4）块第 产品，每件产品的利润为r_i （i=1，2，3，4），则每块原材木板切割产生的最大利润为

其中k_i （i=1，2，3，4）为每块木板最多可切割的第 种产品的个数。

对一块原材料木板进行切割，按木板利用率从大到小给出如下切割方案，计算在不同切割方案下单块木板有效切割产品所产生的利润，则可对不同方法的单位原材料木板有效切割所产生的利润进行从大到小顺序，然后再按照单位原材料木板进行有效切割所产生的利润和这4种产品的单位利润进行综合排序，考虑以单位原材料木板进行有效切割所产生的利润所对应的方案进行切割木板，综合可得总利润最高的切割方案。

3模型的评价

3.1模型优点

在建立过程中，充分考虑了在解决此问题当中的工业生产的实际意义;模型的求解不需要高深的数学知识，更适宜在工业生产中进行推广。

3.2模型的缺点

模型的最后一问根据题意不考虑产品的数量，进一步可考虑在确定产品数量基础上扩展模型。

参考文献

[1]张鹏程.基于BIM体系的钢筋施工深化与下料优化研究[D].福州：福建工程学院，2018.

[2]肖海华.矩形件下料问题的创新线性规划布局方法研究与应用[D].广西：广西大学，2017.

[3]罗强.基于灰狼算法的矩形优化排样及其在板式家具开料中的应用[D].武汉：华中科技大学， 2019.

[4]饶昊.板材切割问题的求解与应用[D].南昌：江西财经大学，2019.

[5]万德福.基于遗传蚁群算法对不定长一维线材切割优化[D].南昌：南昌大学，2020.

[6]郭百海，隋毅.基于排样矩形的直角边零件下料算法[J].计算机系统应用，2021，30（1）：162-167.

[7]季君，邢斐斐，黄敦华.等.解决二维下料问题的最优两阶段排样方式[J].现代制造工程，2021（3）：81-86.