信号干扰条件下超宽带精确定位问题研究

余 丹, 彭博钧, 彭思瑾, 谢文武

(湖南理工学院 信息科学与工程学院, 湖南 岳阳414006;湖南理工学院 南湖学院, 湖南 岳阳 414006)

0 引言

随着移动互联网的发展, 出现了基于位置的定位服务(LBS).定位技术又分为两种, 一种是室外定位技术, 另一种是室内定位技术.全球定位系统(GPS)是目前比较成熟的室外定位技术.我们可以通过这项技术实现移动设备上的各类定位导航服务, 例如驾驶导航、APP 中的定位查找等.室内定位不能采用GPS定位, 因为GPS 系统是测量已知位置的卫星到用户接收机之间的距离, 然后综合多颗卫星的数据计算接收机的具体位置.而在室内, 卫星信号无法穿透建筑物, 且无法确定目标所处楼层.室内定位的方法有多种, 例如基于光学的室内定位、基于声波的室内定位、基于无线电波通信技术的室内定位.

在多障碍物的室内环境下, 超宽带(UWB)信号易受到遮挡干扰而造成定位误差[1,2].UWB 定位主要解决两个核心问题: (1)信号无干扰情况下的定位, 即视距(LOS)定位; (2)信号有干扰情况下的定位, 即非视距(NLOS)定位.本文在给定定位场景的基础上, 围绕上述两个核心问题进行研究.

1 基于粒子群优化算法和卡尔曼滤波的正常数据的定位

针对正常数据建立一个粒子群优化算法(PSO)[3]和卡尔曼滤波[4]相结合的算法模型.首先使用PSO求出靶点位置.由于每个位置有多组数据, 故能得到多个解.卡尔曼滤波是一种递推算法, 其本质是通过前一时刻预测出当前时刻的值, 并使估计值的均方差最小.同一位置采集了多组不同时刻的距离数据, 对各组距离数据使用PSO 求解, 再将各组数据的坐标解使用卡尔曼滤波算法融合, 以获得更精确的距离值.

1.1 粒子群优化算法

PSO 是通过模拟群体协作使种群完成最优目标而建立起来的一种随机搜索算法.PSO 初始化为一群随机粒子, 每个粒子都是极值优化问题的一个潜在解.粒子个体在解空间中计算得到的适应度最优位置被称为个体极值Pbest, 而种群中所有粒子得到的适应度最优位置被称为群体极值Gbest.粒子群通过迭代的方式来寻找最优解.每次迭代过程中, 粒子通过跟踪两个“极值”来更新自己, 并通过位置、速度和适应度值来表示该粒子特征.PSO 算法流程如图1 所示.

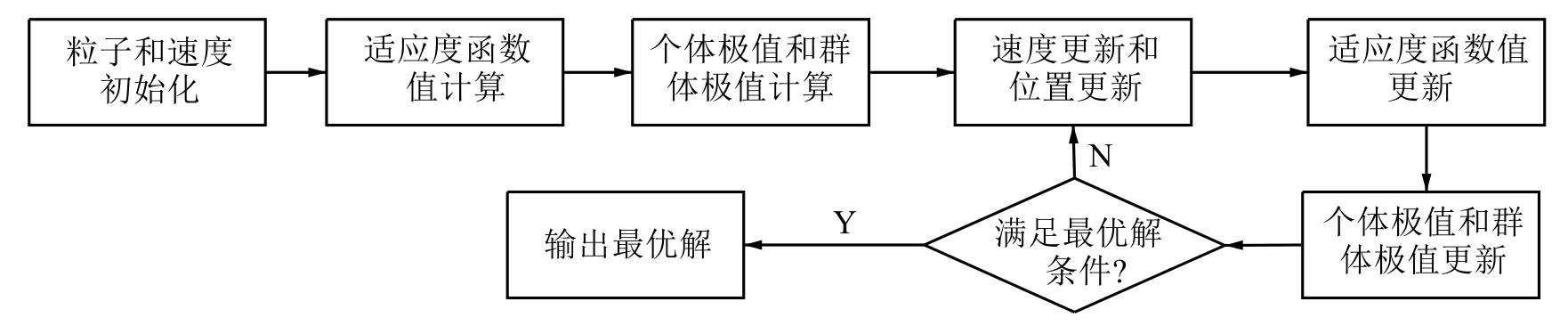
图1 PSO 算法流程

在每次迭代过程中, 粒子的Pbest 和群体的Gbest 更新自身位置:

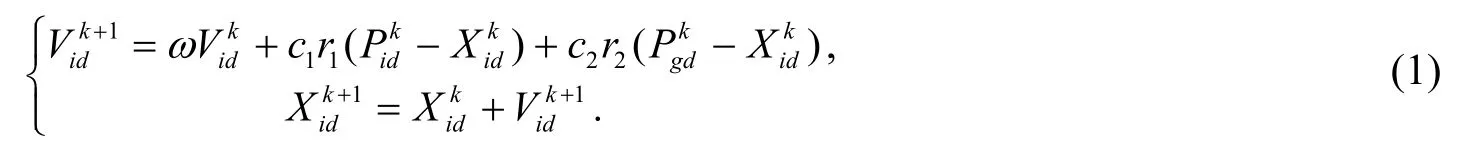
PSO 的目标函数为最小化靶点到锚点距离和测量距离的差的绝对值, 搜索空间为实验场景的三维坐标, 即使得

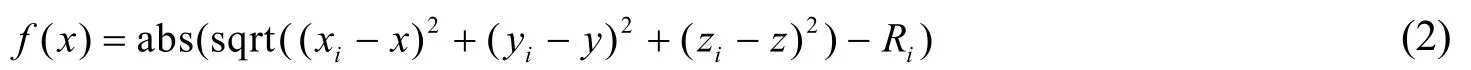
的值最小.其中(x,y,z)为靶点位置坐标; (xi,y i,zi)为锚点位置坐标, 对于正常数据取i= 1,2,3,4, 异常数据取i=1,2,3或i=1,2,4或i=2,3,4或i=1,3,4;Ri为各锚点到靶点的测量距离.

1.2 卡尔曼滤波

在各组数据定位期间, 靶点位置始终不变, 在锚点到靶点距离的测量过程中, 靶点的位置受到加性噪声n(k) 的干扰, 且不同时刻不同数据的噪声互不相关.系统状态方程和观测状态方程为

其中X(k) 表示k时刻靶点的真实位置,Z(k) 为k时刻由PSO 得到的观测值.故X(k) 的最佳估计可由卡尔曼滤波方程得到.

状态一步预测为

状态更新为

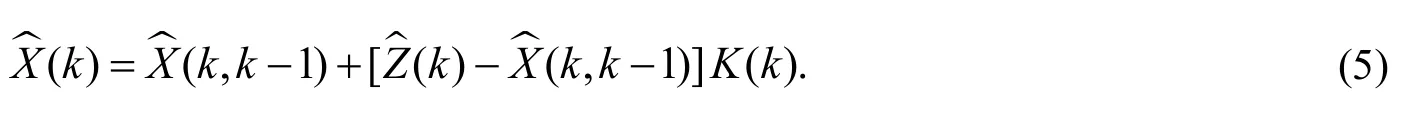
滤波增益矩阵为

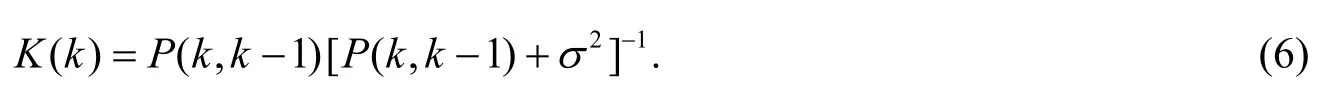
一步预测误差协方差阵为

误差协方差阵更新为

2 基于粒子群优化极限学习机算法的异常数据的定位

UWB 采集信号时通常无法分辨是哪个数据受到了干扰.在异常数据中, 每个位置的数据均存在受干扰的情况, 而此数据在某一时刻只有一个锚点受到干扰.受到干扰后会导致数据偏离正常值的大小, 从而导致定位失败.为了降低干扰, 使用基于粒子群优化极限学习机算法(PSO-ELM), 剔除每组数据中的干扰值, 使用其他的三个锚点进行定位, 从而在受到干扰的情况下也能实现定位功能, 规避在锚点受到干扰时会导致重大定位失误的可能.异常数据算法流程如图2 所示.在求出每组数据的最优解后, 对每个位置所有数据的解取均值, 即可得到最后的位置.

图2 异常数据算法流程

极限学习机(ELM)[5]是一个前向传播的单隐层神经网络, 包括输入层、隐含层和输出层, 可以随机初始化输入权重和偏置.

设有N个样本(X i,ti), 其中Xi=(xi1,xi2,… ,xin)T∊Rn,ti=(t i1,ti2,… ,tim)T∊Rm, 隐含层输出函数满足

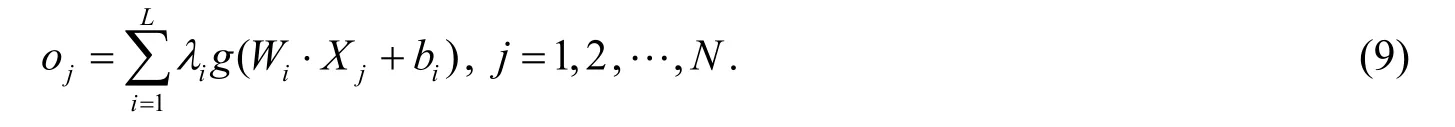
其中Wi为输入权重,λ为输出权重,g(x) 为激活函数.

其目标是使得输出误差最小, 即

即存在λ,W和b, 使得

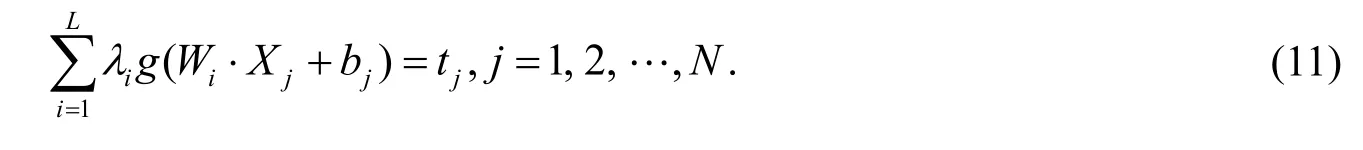
故可表示为

其中T为期望输出, 而

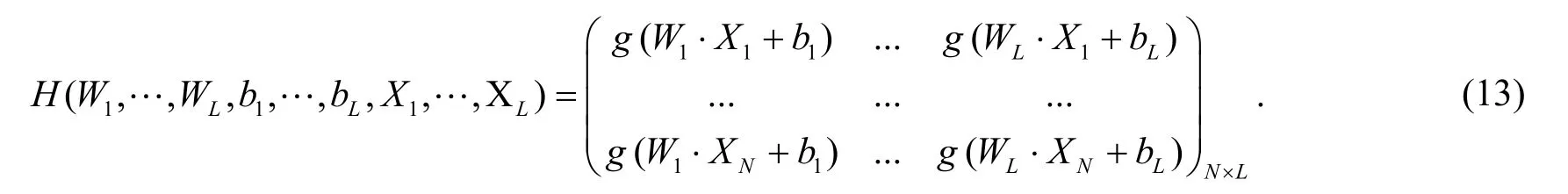
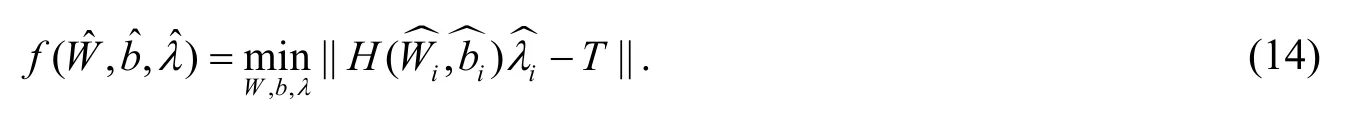
于是其最小化损失函数为

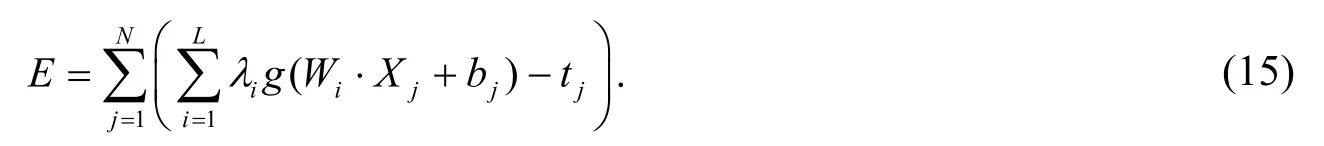
算法基于极限学习机(ELM),主要流程如图3所示.

图3 算法流程

在经过预处理的数据中,取70%作为训练集,30%作为测试集,算法测试结果的正确率为93%, 证明该分类算法有效.图4为对随机抽取的数据进行测试得到的结果.

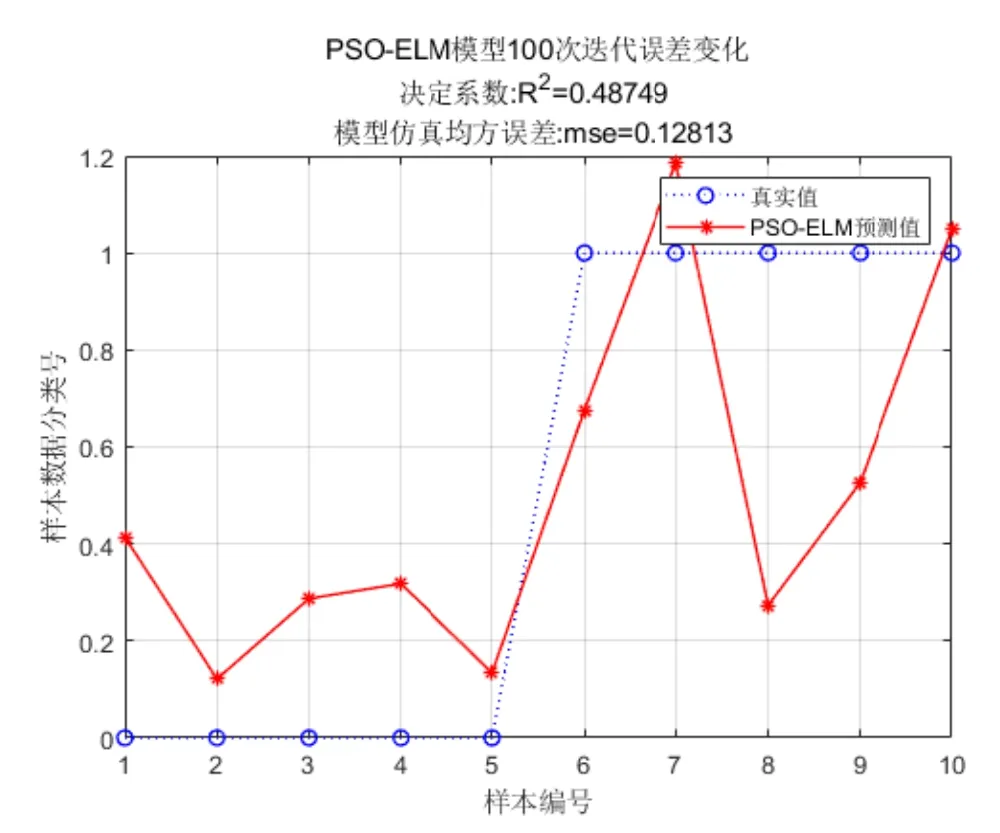
图4 EL M 算法测试结果

3 仿真实验与结果分析

3.1 定位精度评价指标

均方根误差(RMSE)是均方误差的算术平方根,能够切实反映测量结果和真实结果之间的偏差程度.三维坐标下的均方根误差计算公式为

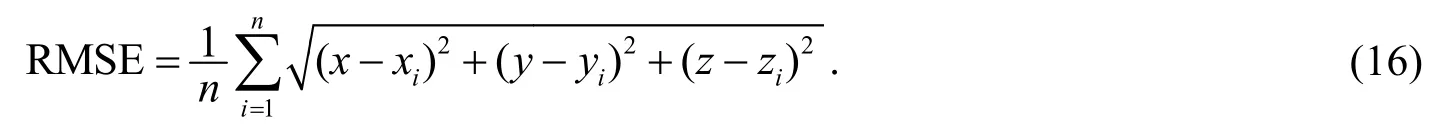
3.2 正常数据的定位结果

对于LOS 环境下的定位(即在4 个锚点均无遮挡的情况下),使用粒子群优化算法求解最优坐标值,再使用卡尔曼滤波融合得到最后位置.二维平面(X-Y)定位结果如图5所示.

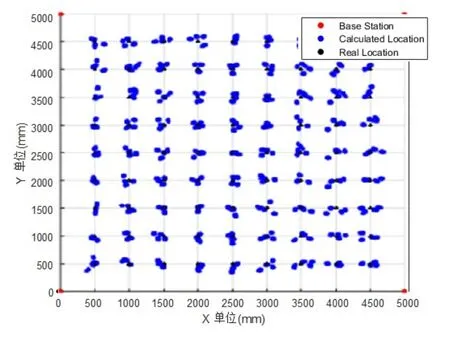
图5 正常数据二维平面定位

一维、二维和三维精度分别如图6、图7和图8所示,单位为毫米(mm).

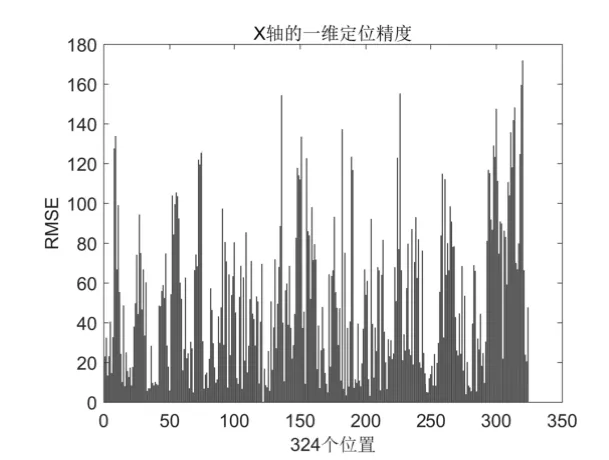
图6 正常数据一维精度

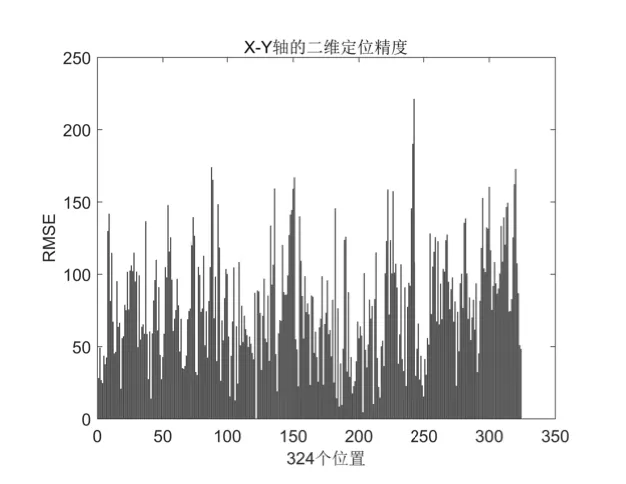
图7 正常数据二维精度

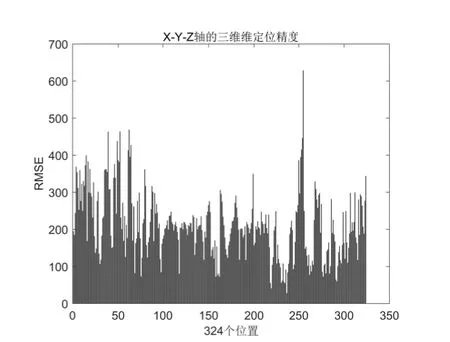
图8 正常数据三维精度

由三维定位精度可知,即使是在LOS环境下采集的数据,在高度通道的定位结果仍不理想,324个位置三维平均误差达到了211.49mm,误差主要体现在高度通道.一维和二维定位精度略好于三维精度,平均均方根误差分别为50.44mm 和78.16mm.

3.3 异常数据的定位结果

对于NLOS环境下的定位(即在4个锚点部分有干扰的情况下),将四组数据三三分组,使用粒子群优化算法分别求解最优坐标值,再使用卡尔曼滤波融合得到最后位置.

异常数据的二维平面(X-Y)定位结果如图9所示.一维、二维和三维精度分别如图10、图11和图12所示.

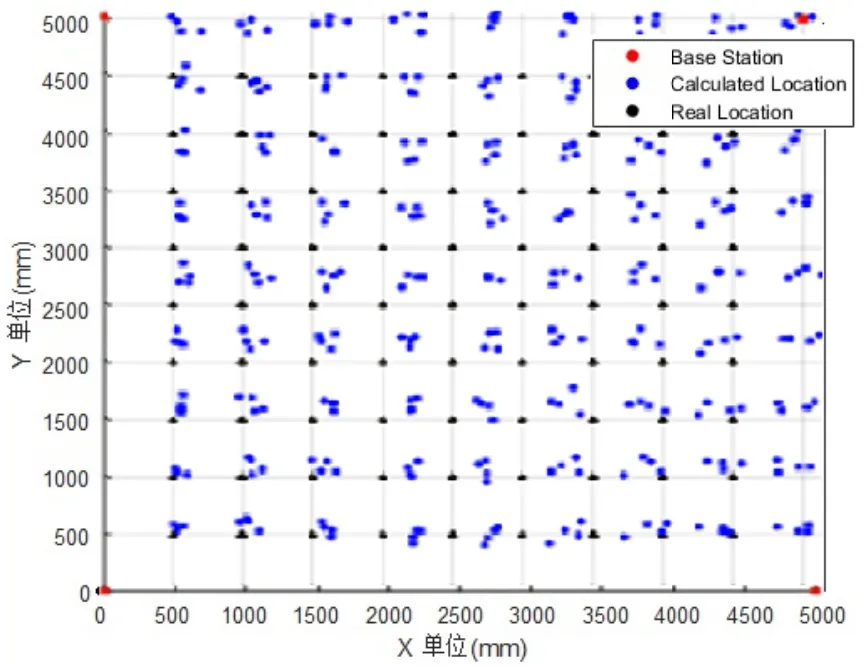
图9 异常数据二维平面定位

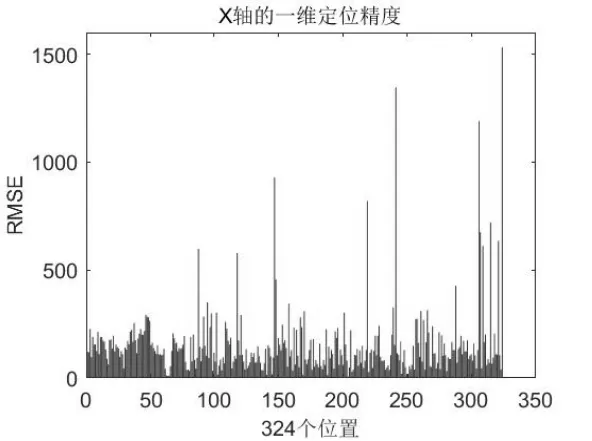
图10 异常数据一维精度

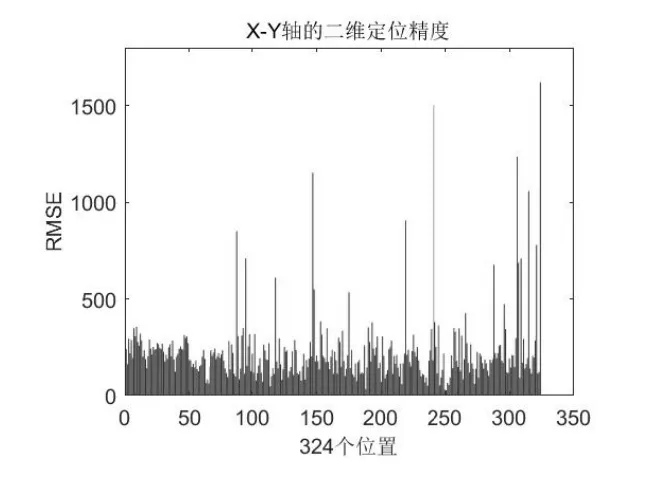
图11 异常数据二维精度

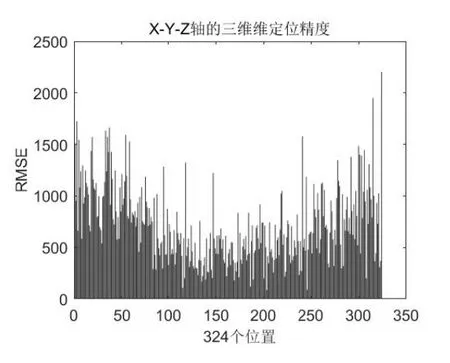
图12 异常数据三维精度

由于有异常数据的存在,当剔除异常数据时,仅有三个点参与定位,故定位的高度通道误差变大情有可原,同样也会对一维和二维精度造成一些影响.324个位置三维平均误差达到了709.15mm,一维和二维定位精度强于三维定位,平均均方根误差分别为153.75mm 和225.85mm.

4 结束语

本文提到的PSO和卡尔曼滤波结合的模型,可以推广至所有基于测量距离的二维平面定位,基于粒子群优化的极限学习机可推广至基于传感器信息融合的室内定位中的姿态和动作识别.