基坑开挖爆破振动信号的小波包分析
何 梦,诸 洲,李贺龙
(1.中核华辰建筑工程有限公司,陕西 西安712000;2.西南交通大学 土木工程学院,四川 成都610031)
0 引言
随着我国经济建设的蓬勃发展和爆破技术的不断进步,工程爆破广泛应用于矿山、水利水电、交通、建筑等领域,成为了一种不可或缺的工程施工手段[1]。 在带来巨大社会经济效益的同时,工程爆破也给周围的人员、设备、建(构)筑物以及环境带来了不可忽略的负面效应。 振动的破坏作用是工程爆破负面效应中最重要的问题之一,已引起众多学者的广泛关注[2-3]。
爆破振动信号具有持时短、突变快等特征,是典型的非平稳信号[4-5]。 得益于信号分析数学方法的进步,小波分析已经成为非平稳信号分析与处理的有力工具。 与小波分析相比,小波包算法在采用小波分析中的尺度和位置参数的基础上,还增加了频率参数,它能随尺度的增大把变宽的频谱窗口进一步分割变细,实现对信号的等带宽分解。 小波包分解的基本思想是将小波分析没有分解的高频部分也同样划分为高频、低频两部分,并依次进行多层分解,它能根据爆破振动信号的特征以及分析的要求来选择与信号频谱相匹配的相应频带,是一种更加精细的分解方法[6]。 鉴于此,为分析不同爆破条件下振动信号的频带能量分布特征,选择满足分析要求的爆破振动信号,对其进行小波包及能量分析。
1 小波包分析基础
1.1 小波基的选择
小波包分析方法中,同一个爆破振动信号采用不同的小波基分析会产生不同结果,因此,选择适合的小波基十分重要。 研究表明,sym8 小波基具有良好的紧支撑性、光滑性和近似对称性,是分析爆破振动非平稳信号的最优小波基。
为了检测sym8 小波基的信号重构精度,选择现场测试得到的一个爆破振动信号的径向速度时程曲线作为分析样本,爆破条件,如表1 所示。 利用sym8小波基对其进行小波包分解与重构,原始信号、重构信号以及信号误差,如图1 所示。

表1 所选信号对应测点的爆破条件
观察图1 发现,原始信号和重构信号的误差数量级为10-12,误差较小,因此确定采用sym8 小波基作为基函数来进行爆破振动信号的小波包分析。
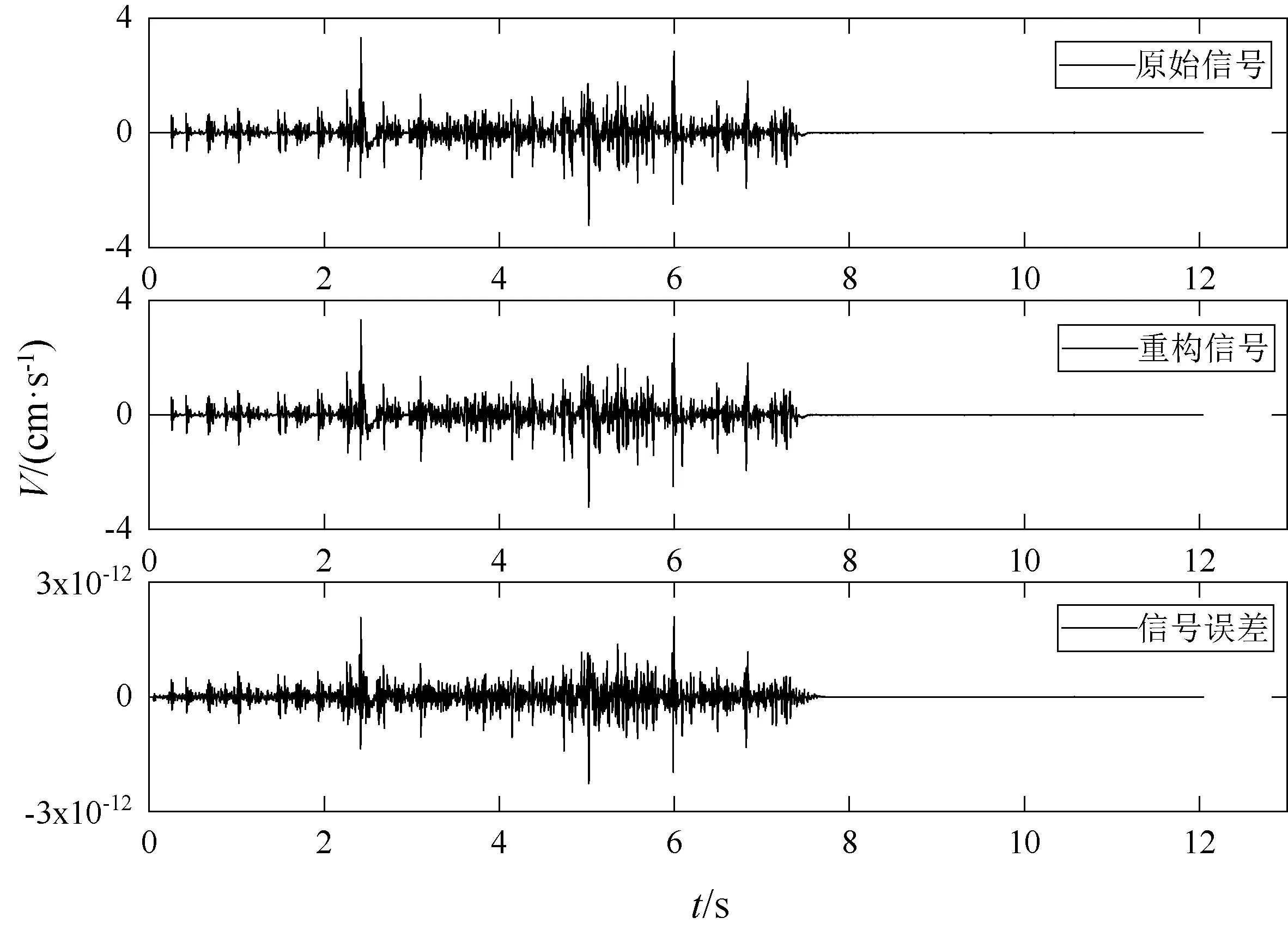
图1 原始信号、重构信号以及信号误差时程曲线
1.2 分解层数的确定
爆破振动信号的小波包分解层数受爆破振动测试传感器最小工作频率的影响,当分解频率小于记录仪的最小工作频率时,信号可能会失真,所以爆破振动小波包分解层数取决于记录仪的最小工作频率。 本次爆破振动现场测试选用的记录仪最小工作频率为5 Hz,采样频率设置为5 000 Hz,由香农采样定理可知,奈奎斯特频率取2 500 Hz。所以,根据小波包分解原理,此处将爆破振动信号进行尺度为9 的小波包分解,得到的频带宽度依次为: 0 ~ 4. 883 Hz, 4. 812 5 ~ 9. 766 Hz, …,2 495. 117 ~5 000 Hz。
2 爆破振动信号的各频带能量分布计算方法
由1.2 节可知,爆破振动信号的小波包分解深度为9 层,第9 层小波包重构信号各频带f9,j对应的能量E9,j可按下式计算:
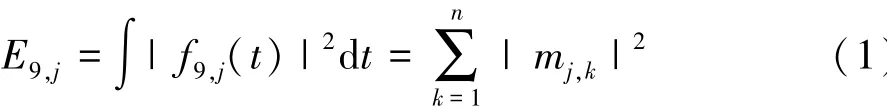
式中:mj,k(j=0,1,2,…,29-1;k=1,2,…,w;w为信号离散采样点数)为第9 层重构信号离散采样点对应的幅值。
所以,信号总能量Ea可表示为:

第9 层重构信号各频带能量所占比例可表示为:

式中,j=0,1,2,…,29-1。
由式(1)~(3)可求得小波包分解和重构后的爆破振动信号各频带能量、总能量和各频带能量百分比,各频带能量分布计算程序框图,如图2 所示。
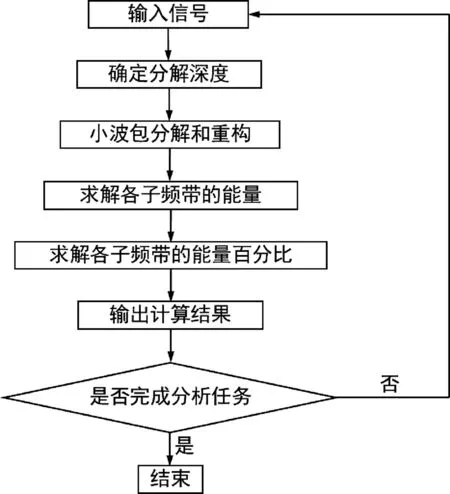
图2 爆破振动信号各频带能量分布计算的程序框图
3 不同爆破条件对信号能量分布特征影响分析
3.1 爆心距对能量分布的影响
本小节分析爆心距对振动信号频带能量分布的影响,为排除最大段药量和爆破排数的干扰,此处选取最大段药量均为210 kg,爆破排数均为25 排的3 条爆破振动信号进行分析,其爆破条件,如表2 所示。

表2 所选信号的爆破条件
根据小波包分析原理和各频带能量计算方法,在MATLAB 软件中编制程序,对所选择的爆破振动信号分别进行尺度为9 层的小波包分析,得到各个频带的能量分布,如图3 所示。 由图3 可知,310 Hz 以上的能量很少,所以此处仅统计310 Hz 以内的各频带能量百分比作为分析依据,各频带能量分布百分比如表3 所示。
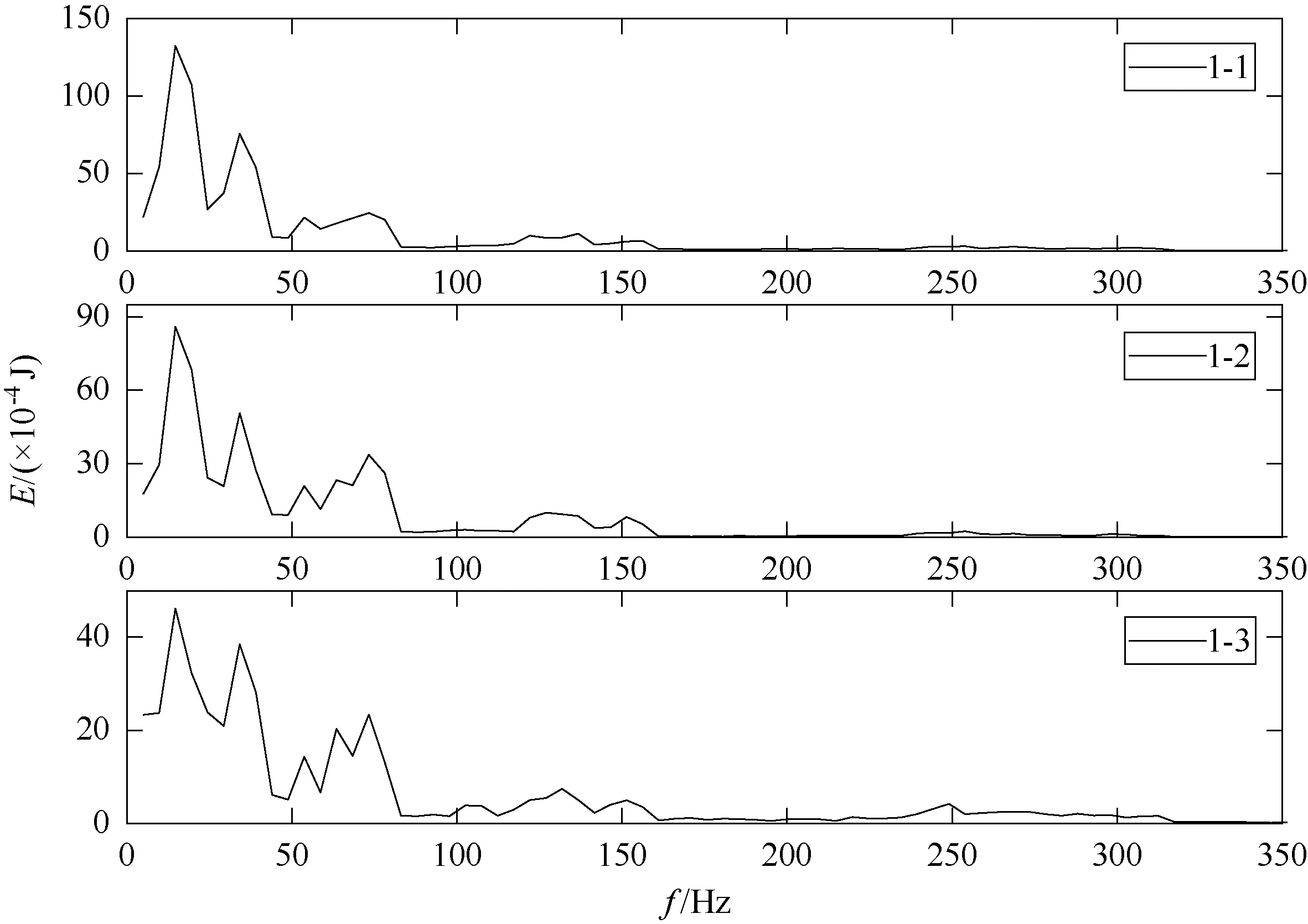
图3 所选信号各频带的能量分布
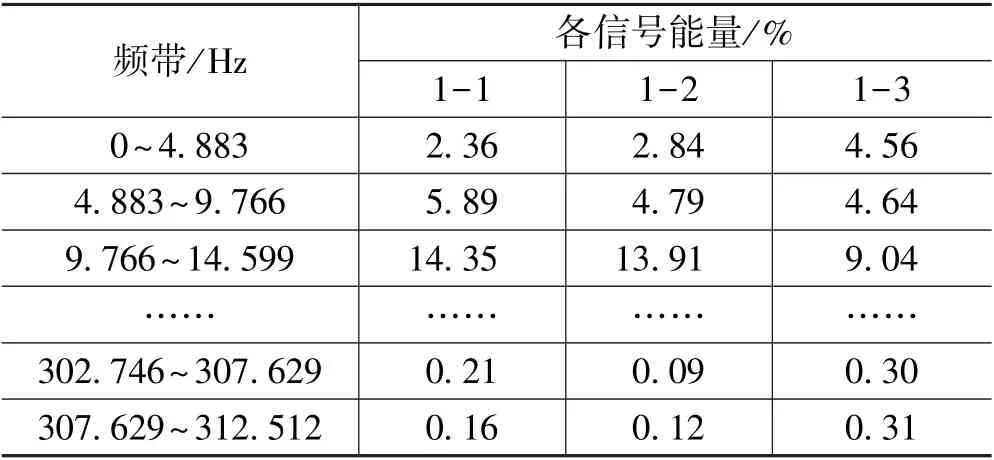
表3 爆破振动信号频带能量分布百分比
观察图3 发现,爆破振动信号的频带能量整体呈现出随频率的增大而逐渐减小的趋势。 各爆破振动信号的能量主要分布在中低频带(0 ~80 Hz)以内,中低频带的能量峰值高,其能量幅值随频率的变化而迅速变化;中高频带(80 ~310 Hz)的能量分布较少,能量峰值低,其能量幅值随频率的变化而缓慢变化。 爆破振动信号的频带能量分布随爆心距的增加主要表现出以下特点:(1)随着爆心距的增加,爆破振动信号1-1,1-2,1-3 的总能量不断衰减,能量峰值逐渐降低;(2)爆破振动信号1-1,1-2,1-3 的中高频带(80~310 Hz)能量分布逐渐增多,说明爆心距越大,信号的能量分布越发散,其主振频带宽度越有增大的趋势。
观察表3 发现,信号1-1,1-2,1-3 的极低频0 ~4.883 Hz 能量占总能量的百分比分别为2.36%,2.84%,4.56%,中高频(83.011 ~312.512 Hz)的能量占比分别为14.46%,16.33%,20.32%。 随着爆心距的增加,爆破振动信号的极低频能量和中高频能量所占比例增大,说明爆心距越大信号能量分布越发散。
3.2 最大段药量对能量分布的影响
为分析最大段药量对爆破振动信号能量分布的影响,此处选取爆心距和爆破排数满足要求的3 条信号进行分析,其爆破条件如表4 所示。
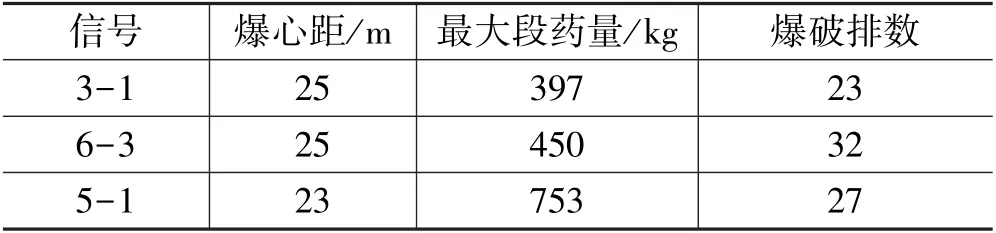
表4 所选信号的爆破条件
对所选择的爆破振动信号分别进行尺度为9 层的小波包分析,得到各个频带的能量分布如图4 所示。 由图4 可知,310 Hz 以上的能量很少,所以此处仅统计310 Hz 以内的各频带能量百分比作为分析依据,各频带能量分布百分比见表5。

表5 爆破振动信号频带能量分布百分比
由图4 可知,爆破振动信号的频带能量分布较分散,中低频带(0 ~80 Hz)能量分布较多,能量峰值大,能量幅值随频率的变化而快速变化;中高频带(80 ~310 Hz)能量分布较少,能量峰值低,能量幅值随频率的变化而缓慢变化。 随着最大段药量的增加,爆破振动信号的频带能量分布主要表现出以下特点:(1)信号3-1,6-3,5-1 的能量峰值对应频率逐渐降低,说明爆破振动信号的能量峰值对应频率随着最大段药量的增加而降低。 由于建(构)筑物的自振频率较低,当爆区附近有被保护的建(构)筑物时,应当严格控制最大段药量,以确保爆破过程中建(构)筑物的安全。 (2)随着最大段药量的增加,爆破振动信号3-1,6-3,5-1 的能量分布逐渐向中低频带(0 ~80 Hz)集中,其主振频带宽度有减小的趋势。

图4 所选信号各频带的能量分布
由表5 中的统计数据可知,信号3-1,6-3,5-1的中低频带(0 ~83.011 Hz)能量占总能量的百分比分别为49.85%,58.48%,60.11%,极高频带(大于312.512 Hz)的能量占比分别为25.43%,19.66%,16.01%。 随着最大段药量的增加,信号的中低频带能量增大,极高频带能量减小,说明最大段药量增加会导致信号能量向中低频集中,使爆破振动信号的主振频带减小。
4 结论
利用小波包分析技术对爆破振动信号进行分析,分别探讨了爆心距、最大段药量以及爆破排数对爆破振动信号能量分布特征的影响,从能量的角度分析了爆破地震波的传播机制,得到的主要结论如下:
(1)爆破振动信号在由近及远的传播过程中,总能量不断衰减,能量峰值逐渐降低,信号的能量分布发散,其主振频带有增大的趋势。
(2)随着爆破最大段药量的增加,信号能量峰值对应的频率逐渐降低,能量分布向中低频带(0 ~80 Hz)集中,其主振频带宽度有减小的趋势。

