汽车装配车间流水线物料问题配送研究*

张若冰，田 博，孙源龙，常 亮※

（1.西藏大学理学院，拉萨 850000；2.西藏大学信息科学技术学院，拉萨 850000）

0 引言

汽车制造有冲压、焊接、涂装和总装四大关键工艺，其中总装车间的占地面积最大、工人数量最多，迫切需要数学建模技术帮助降本增效。总装指将内外全部饰件装配到车身上的一种工艺，通常围绕流水线展开，线上的每个工位负责装配固定的物料。为防止停线影响生产效率，需要及时补充工位上的物料，此物料补充工作称为运输，一般由拖车完成。拖车接收到任务指令后，需要进行如下操作。（1）取料：前往目标物料的存储位，将物料装载至拖车；（2）配送：将物料运送至目标工位和卸载。需要注意的是，在不超过小车容量的情况下，多个任务可同时进行。

刘奎武等［1］研究的组合药装盒多向输送生产线的问题，较好地解决了多条流水线之间的货物运输问题，但不适合原料到生产工位之间的运输问题。厦门大学的杨钰琳[2]以0-1整数规划问题研究的汽车公司总装混流装配线平衡问题，使得混流总装线的运行更加平稳和高效。但是没有满足本题目中的工位分区和仓储点到生产工位的约束条件。

本文研究的问题假设将两条流水线上的工位分成若干个区域，并由一个小车负责此区域的货物搬运，将III区对应序号的货物搬运至I区和II区对应编号的工位进行生产，具体分布如图1所示。

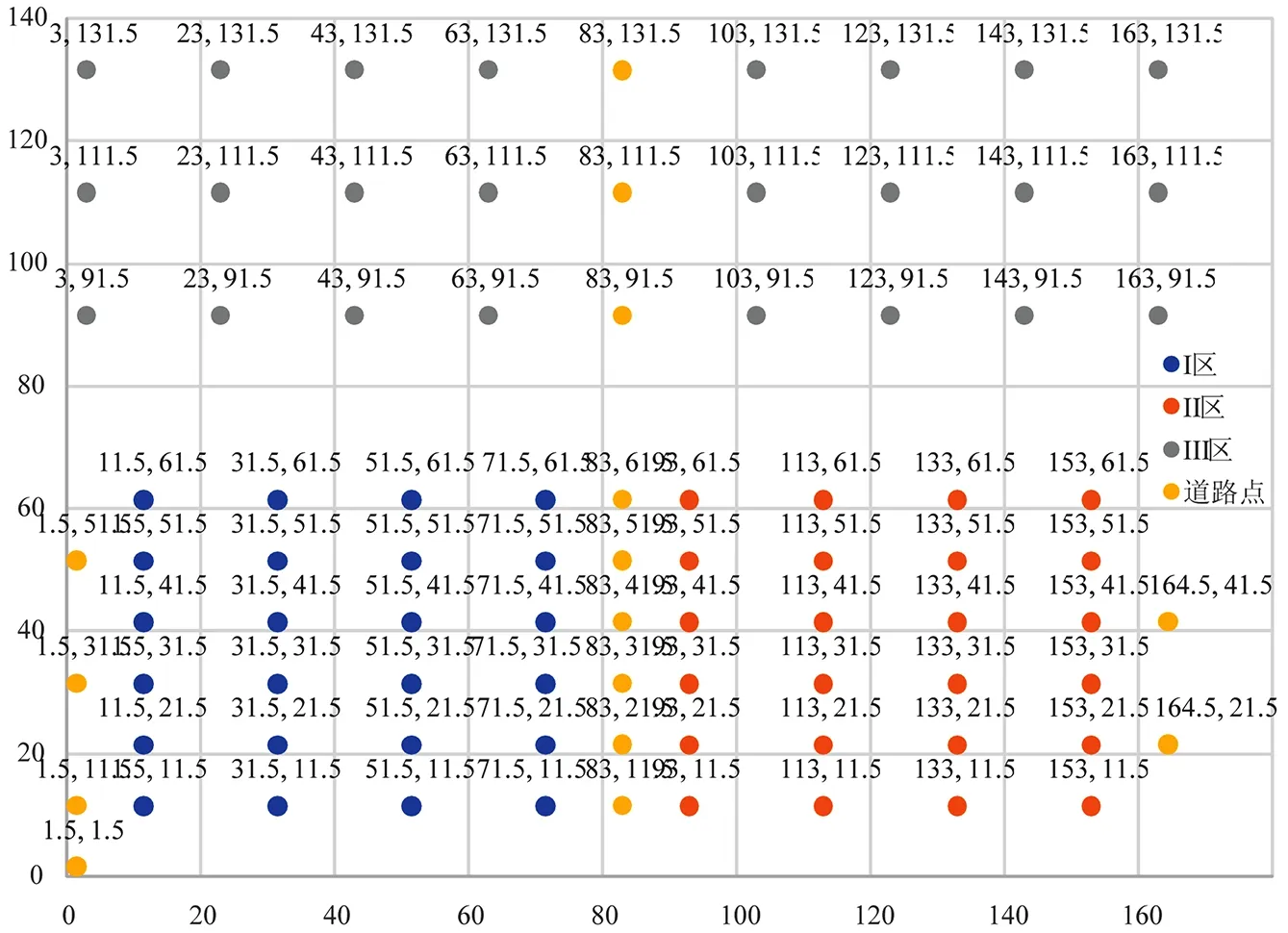
图1 有效点分布

在规划配送路线较短的方法中，本文采用蚁群算法，将搜索的过程不断收敛，直至找到最优解，在搜索路径问题上具有优势。多项活动同时运算，极大地提高了运行效率。并对传统蚁群算法进行了改进，在约束条件中添加了时间窗，降低了流水线停线的可能。

1 转运车辆分组

由于流水线区域可使用的拖车数量有限，为了避免拖车路线可能出现的情况过于复杂繁琐，需要首先对拖车进行分组后再进行流水线货物调配。

1.1 广度优先搜索分配方案

广度优先算法是图搜索算法中常见的一种，以客观的方法搜索图中数据的所有顶点，并计算从起始点到各顶点所需遍历得到的最小边数值[3-4]。其属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止[5]。

在I区域和II区域，相隔两个工位点的距离在水平方向上为20 m，两个工位之间的距离在垂直方向上为10 m；在III区域，相隔两个工位点的距离在水平方向上为20 m，两个工位之间的距离在垂直方向上为20 m。故在计算过程中，可认为其为矩形区域进行计算，最后通过计算其在横向和纵向的行走步数来计算其距离，具体流程如图2所示。根据图中所示流程，对48个工位分别进行路线规划，途径工作点和路线如表1所示。

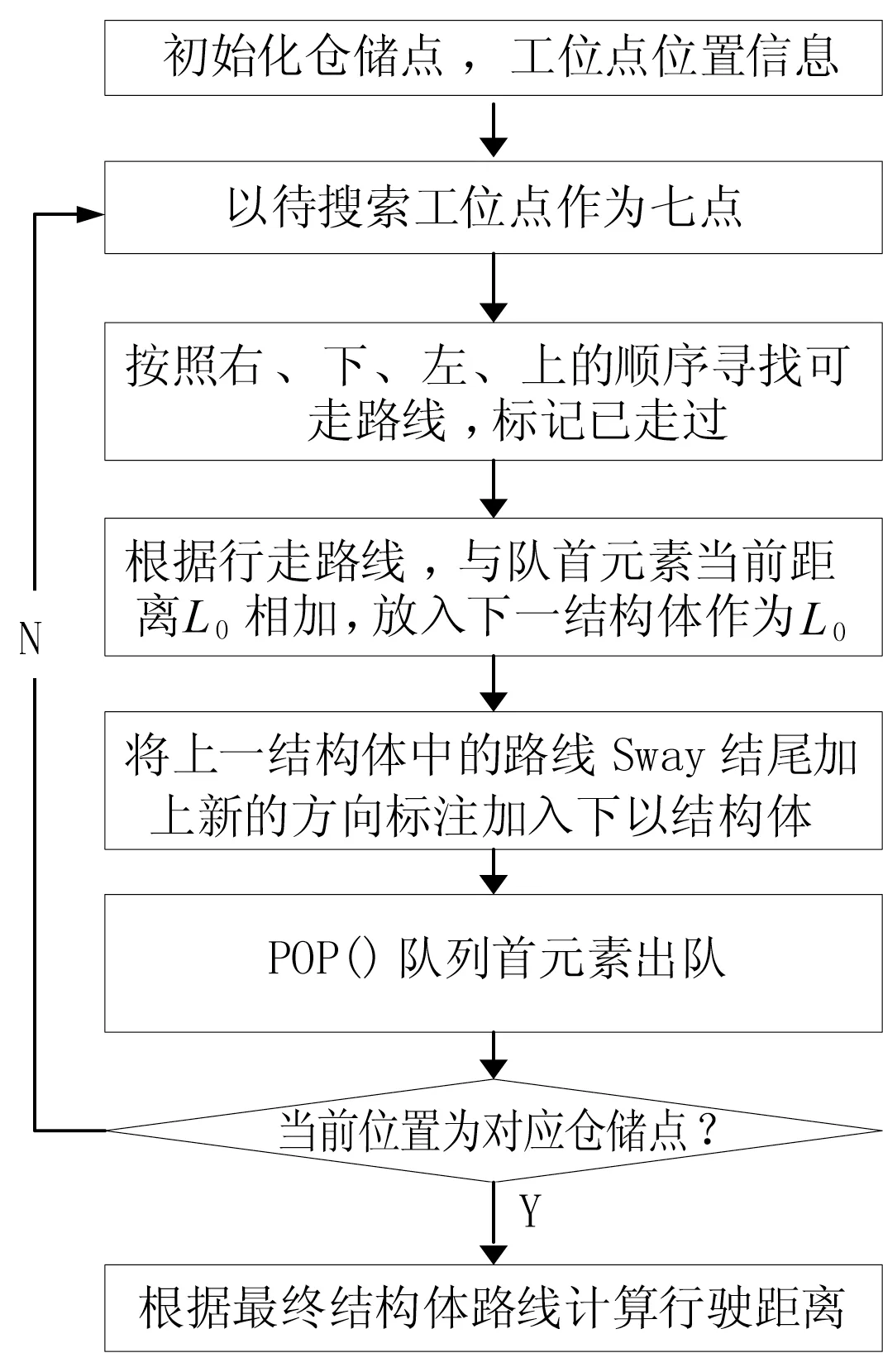
图2 车辆调度路线最短距离计算方法流程

表1 路线规划结果（部分）

1.2 TSP模型分配方案

TSP问题是在信息学竞赛问题中，常见的图论经典组合优化问题。

问题假设有72个点（48个工位点和24个储货点），点i和j之间的距离Ci,j，目标是找到一条闭合的路线，并保证这条路线的总距离最短。这个问题就可以描述成将若干个点认为一个集合V={1,2,3,…,n}。顶点之间的距离为：

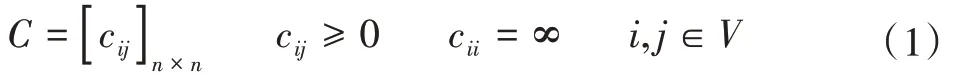
事实上，对于任何两个点i和城市j来说，要么这条旅行路线包含该路线，要么不包含该路线。故引入0-1变量xij，1表示包含该路线，0表示不包含该路线。即目标就是在求：

而在本模型中，由于货物调配过程中，走得不一定是闭环路线，因此在建模中，可以去除TSP模型中的消除约束。从而引入了DFJformulation模型对问题进行了求解。则TSP的整体规划模型为：

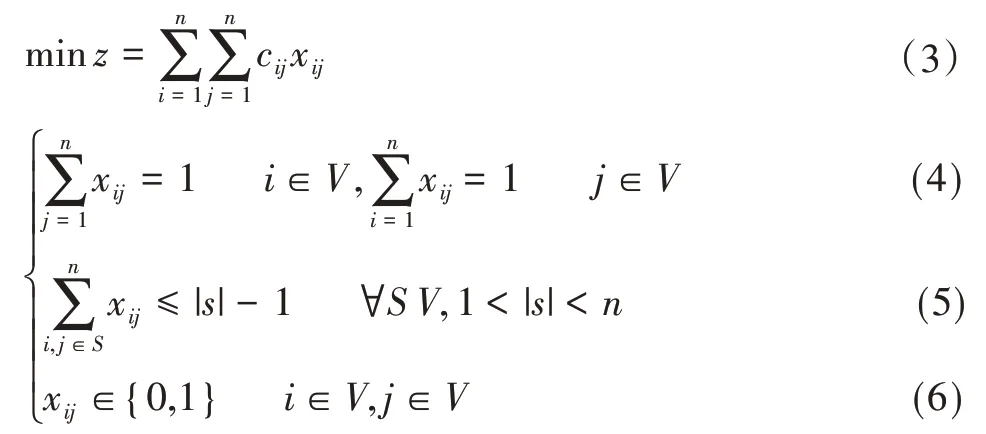
经过DFJ进行处理，以拖车的行驶路线最短为试探性条件，对其承包区进行划分，得到结果如表2所示。

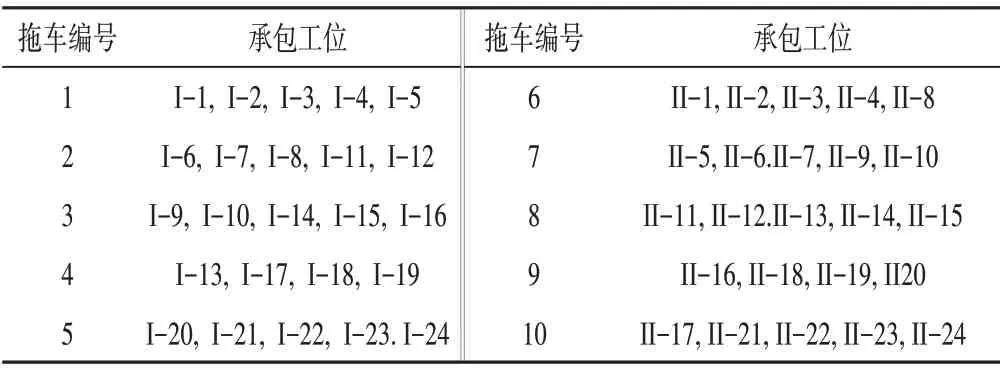
表2 基于TPS的承包区划分结果Tab.2 Division results of contracting area based on TPS

1.3 结果分析和检验

经过对比，发现两种方案得到的结果中，只有I-7和II-6的划分区域存在差异，说明模型合理、结果准确。经过实际分析，推测可能差异来自于路线行驶方案中，方法二并未考虑每辆车到达其目标的对应仓储点的最优路径，而是单纯考虑了整个闭环路线的距离和最短造成的。所以最终以BFS得到的分配方案为最终方案。

2 物料调配方案规划

在本文研究的汽车组装车间物料配送问题中，设R={r1,r2,…,r24}代表24个工作位点以O为坐标原点的位置，而S为道路关键节点的点集，记为S={sA,sB,…,sN}，先有24个不同配料的仓库，要进行物料配送的工作点记为N(i=1,2,…,N)以及所需的拖车数量，每量拖车装载4个工作点的物料量，且每辆小车可以运送多个工位，同时每个工位可以由不同车辆进行运送即不采取承包制运行，当工作位得到足够原料后即为配送任务结束，在物料运送过程中。在尽量减少停线现象的发生并满足约束条件的情况下，建立以配送总成本最低为目标的配送拖车路径优化模型。

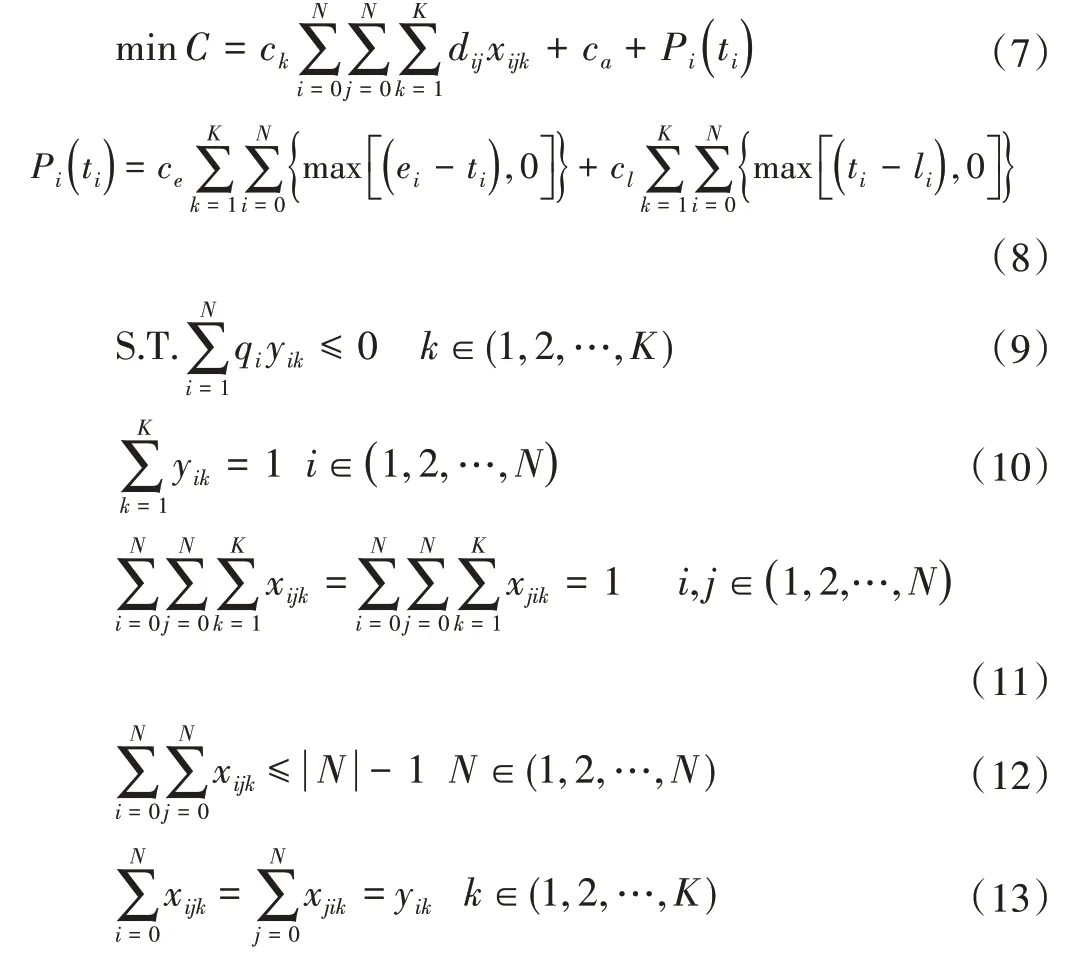
决策变量为：

以上构建的关于路径优化的数学模型中，式（8）中包含了配送拖车的行驶成本与软时间惩罚成本，将其作为本次规划模型的总成本；式（9）表示配送小车能够配送的物料量小于最大限度，在本题中以最多运载4个工作点的物料量为准，即Q≤4；式（10）表示只能由一辆小车完成一个工位其工作点物料的物料配送，排除两辆车同时为一个工作点配送物料的情况；式（11）表示仅从仓库到达工作点完成装卸即为完成整个配送流程；式（12）表示将支路进行消除；式（13）表示到达的配送拖车与离开工位的为同一辆；最后式（14）～（15）为决策变量。

Maro Dorigo模拟自然界中蚁群觅食过程中搜寻可行路径的方式提出蚁群算法，其全局优化能力较强，因此非常适合用于优化sink移动距离[6-7]。而本题目中和传统的蚁群算法还存在着时间窗和路线的限制，因此在蚁群算法训练过程中，还加入了时间窗时序限制和广度优先搜索算法对其路线的是否联通进行判断，避免出现由于连通性问题导致的路线无法行驶，出现的路程差造成了结果的错误。

蚁群算法是基于自然界中蚁群的觅食活动建立的[8-9]。蚂蚁寻找食物的运动过程中会释放一种信息素，蚁群根据信息素可以确定从蚁巢到食物的路线。在单位时间内，路径越短，到达的蚂蚁越多、信息素浓度更高，蚁群趋向于信息素浓度更高的路径，即可以找到到达食物的最短路径。这个过程的本质可以概括为以下几点：（1）信息素浓度越高，被选中的几率越大，以此作为蚁群算法中路径的选择机制；（2）更新后的路径越短，该路径上的信息素增长越快；（3）蚂蚁个体之间通过信息素交流，以此作为蚁群算法中的协同工作机制。

2.1 计算方法的设计和计算机实现

将本题目需求与蚁群算法相结合，以48个工位、24个仓储点为限制条件，按照问题一中划分的承包区结果。图3所示为调度方案生成流程。

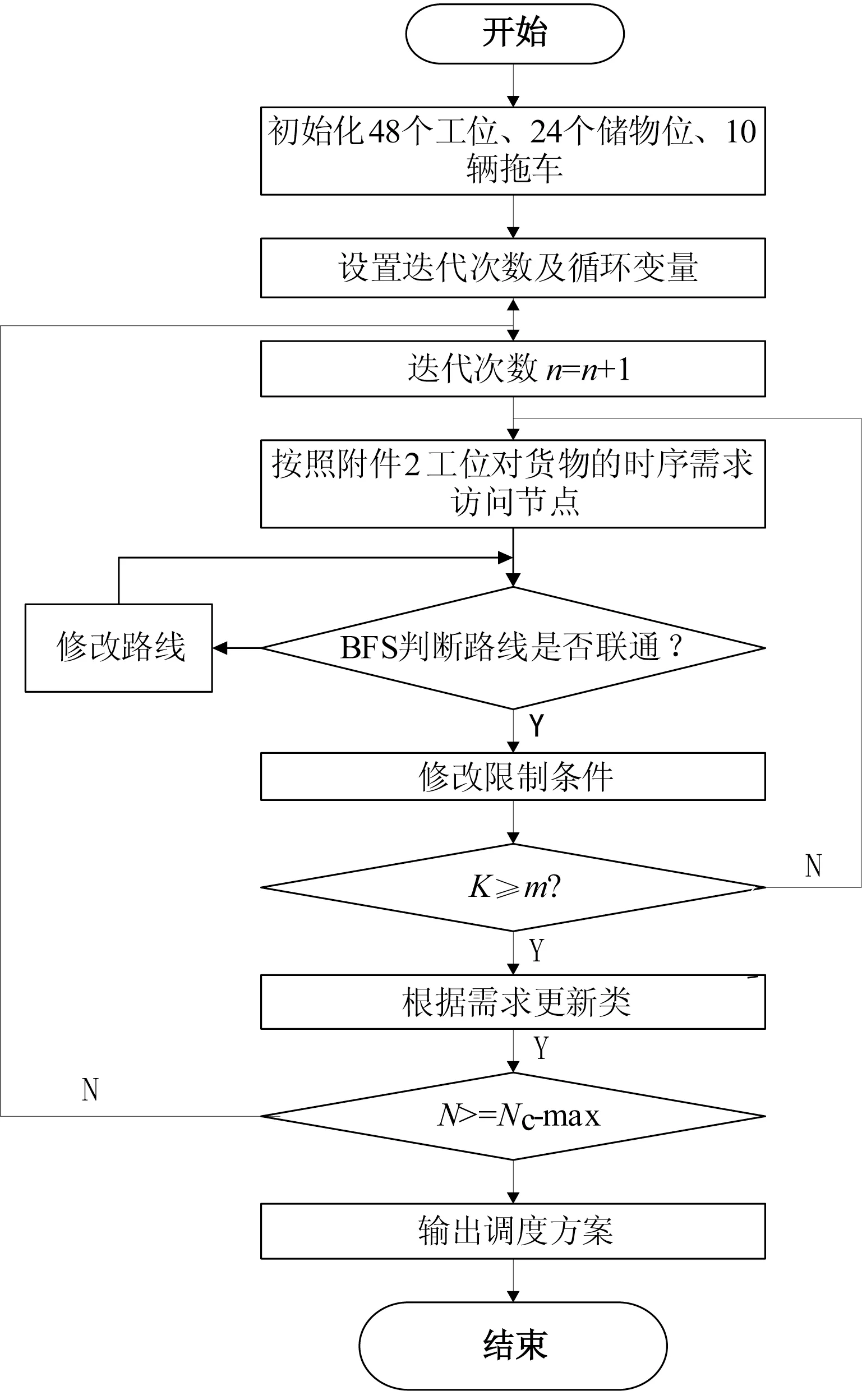
图3 调度方案生成流程

2.2 方案测试结果

假设有6辆可用拖车，23个节点有货物需求，具体需求用例如表3所示。

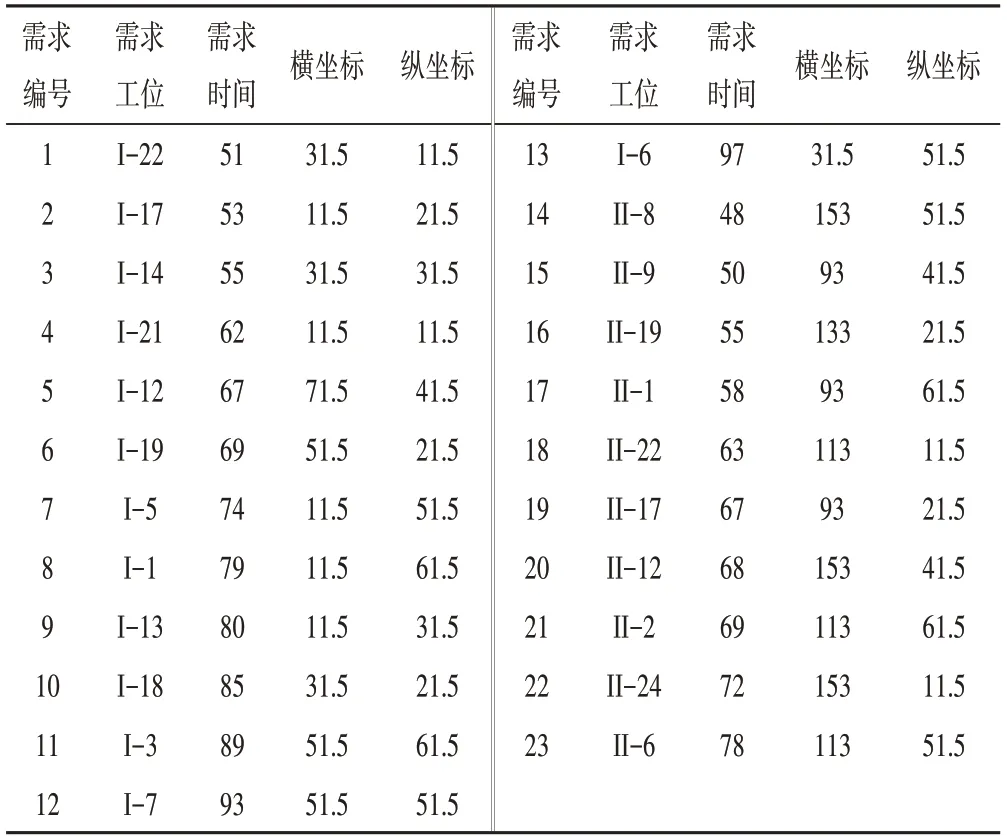
表3 任务训练测试集

根据上述方法及其限制条件，得到了如表4所示的规划方案。由表可知，拖车1出现了在第72 s完成工位I-19的配送后，无法在79 s前顺利达到I-1位置，导致了I-1工位缺少原料，出现2 s的停线情况。通过分析是由于在模型中对时间窗宽度较小的工位进行转移导致的。

表4 任务结果

3 停线问题优化

随着工作的进行，设工位点i其时间窗宽度为widthi=li-ei，在该转移规则下，配送拖车会优先选择配送时间窗宽度差相对较小的工位点，其中pkij(t)表示蚁群算法中蚂蚁k从工位点i转移到工位点j的状态转移概率，则转移规则如下：

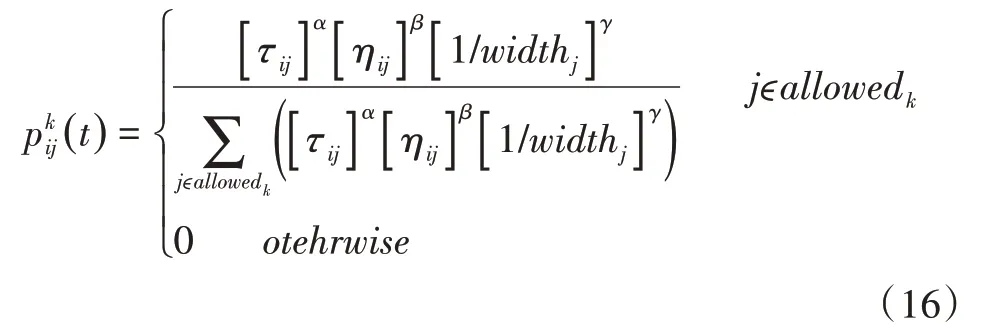
式中：τij为信息素浓度；ηij为启发式因子，ηij与dij的关系为；α为该轨迹的相对重要性，即为信息素的加权值；β为能见度的相对重要性，即为能见度的加权值；γ为等待配送的工位服务顺序，也就是时间窗跨度的重要因子。其为随机变量并在[0，1]上服从均匀分布；allowedk为蚂蚁k在下一步移动中可以选择的点的集合[10]，从而求出状态转移概率，选用轮盘赌法计算选择下次移动的工位点j的概率，直至配料运送完毕，之后使另一辆车继续上步，直至所有配送工位点被访问完成为止。

除此之外，本团队还在蚁群算法中添加了所有蚂蚁完成移动返回原起点后，对残留于路径上的信息素再进行不断更新，因此路径（i，j）在时刻t+1时的信息量可进行进一步调整为：

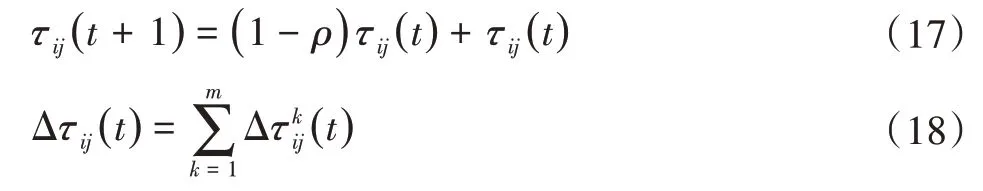
式中：信息素在路径（i，j）上的增量是信息素蒸发因子；ρ为信息素蒸发因子；(1-ρ)为信息素残留因子[11-12]；Δτij(t)为信息素在路径（i，j）上的增量；在初始时刻，Δτij(0)=0，Δτkij为在这个循环中，第k只蚂蚁在路径（i，j）上留下的信息量，若蚂蚁没有经过次路径，则Δτij=0，Δτij表示为：

将上述转移规则进行调整后，本模型再次对上述假设进行方案分配，测试结果如表5所示。通过对转移规则改进对任务的配送方案分配结果可见，改正后的新方案，最终分配的方案避免了停线的情况，也降低了停线的风险。

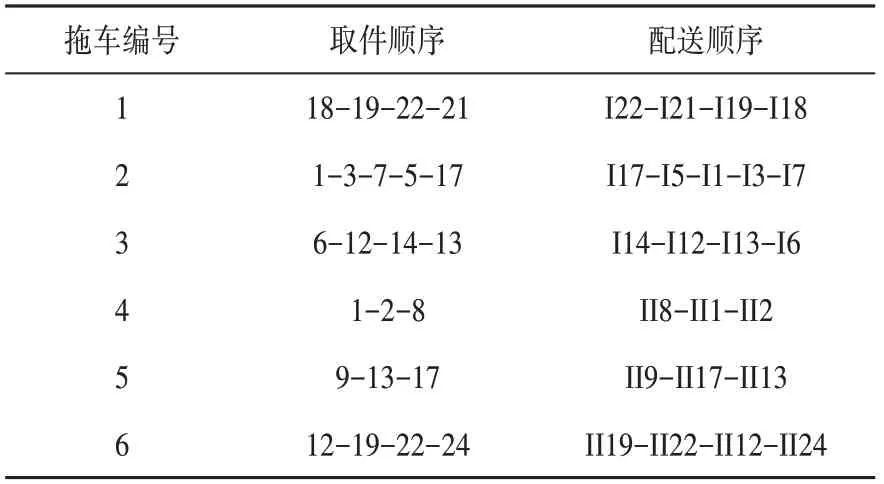
表5 任务3结果（基于改进模型）

4 结束语

本文通过对有限转运条件和储存位置固定的生产流水线进行问题假设，并针对问题将有限的转运能力分配到不同的生产工位，从而更好地利用优先的转运能力；并针对有限的转与能力，通过多模式优化和动态规划模型，规划物料仓储点最少的储存方案，采用蚁群算法进行了转运方案的规划，同时针对停线的风险，引入软时间惩罚成本进行了针对性的优化，增添了路径信息素不断更新的机制。在贴近实际的同时，通过模拟任务需求表明该方法对于流水线的配送问题存在较好的解决能力。