基于双目手眼相机的自动化精度测试系统

唐艳慧，任 宏，刘巧元，姜金辰，王 帅，孙海江

（中国科学院长春光学精密机械与物理研究所，长春 130033）

0 引言

视觉测量技术根据相机获取视觉测量的信息从而对目标的位置和姿态进行测量。通过相机获得目标图像生成匹配的像对，再利用目标在相机左右目的视差及模型参数反推其在三维坐标及位姿。相机和双目模型就是对上述过程的数学描述。在执行空间操作任务时，首先需要获取的就是目标航天器与服务航天器的相对位姿和运动等信息。视觉测量精度有精度高、隐蔽性强、体积小、设备相对简单、成本低等优势，成为首选测量方法。机器视觉因具有灵活性被广泛应用在各种控制系统中，而视觉位姿测量作为核心的视觉技术得到广泛关注。

近些年，航测相机在航天航空任务中占有核心地位，相机性能指标直接影响获取信息的准确性。在航测相机研制过程中需要对其内外参进行严格校准，测试相机精度从而实现精确定位[1]。位姿测量精度是相机重要指标之一。现有的精度测试方法多为单点测量，不仅慢且覆盖面小。精度测试的指标应在使用前进行严格检测，保证其达到设计要求[2-3]，为后续执行任务做好保障工作。本实验提供了自动化位姿测量相机精度测试平台，克服现有的精度测试问题，可以多点，多位移，多角度，全视场进行精度测试。且可以调节目标运动速度同时进行视觉捕捉实验。为今后同类型的平台提供参考价值。

1 手眼相机平台

随着航天、航空事业发展，机械臂成为无人机或辅助航天员出舱工作的重要设备，位姿测量手眼相机作为机械臂视觉引导，视觉伺服的重要组成部分[4-6]，根据实际需求设计了手眼相机自动化精度测试系统。视觉模块如图1所示。

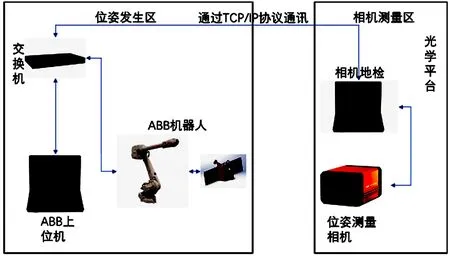
图1 视觉模块示意图

工业机器人选用不确定度为15μm的IRB-2600型号的ABB工业机器人，通过上位机指令控制机械臂运动，手眼相机实际应用如图2所示。通过上位机机械臂与相机采集的位姿互相通信，从而达到自动化测试的效果。

图2 手眼相机实物

2 手眼相机自动化测试系统

2.1 相机标定

双目立体视觉是基于三角原理进行三维信息的获取，基于视差原理的一种方法。该过程可以模拟人眼的立体感知过程。目标是求出三维空间中目标物体相对于相机坐标系的三维坐标，用来进行后续的坐标变化以及机械手控制。

图3所示为双目立体视觉系统三维模型图，相机左右目的投影中心连线的距离为基线，用B表示。相机左右目同时观看物体P时在相机的成像点分别为(pleft=Xleft,Yleft)；(pright=Xright,Yright)。将相机放置同一平面上，成像点P的Y轴坐标是相同的，故Yleft=Xleft=Y。由三角关系可以得到如下关系式：

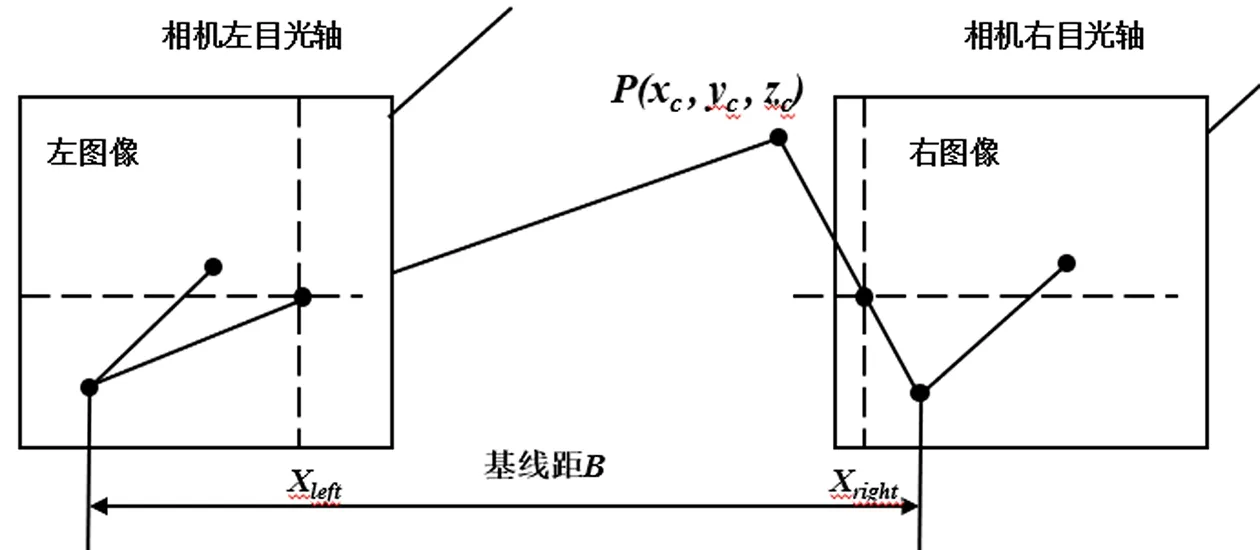
图3 双目立体视觉系统三维模型

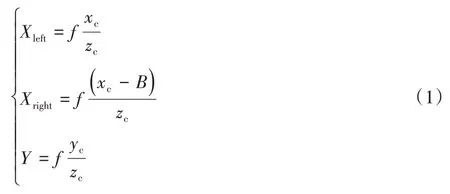
视差被定义在相同点相机左右目X轴向的偏差，即：

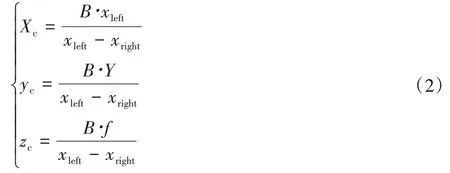
通过上式即可求出空间中任意一点三维空间中的坐标。

张正友相机标定方法选用棋盘格作为相机的标定板。在标定的过程中，假定标定棋盘格所在的平面为世界坐标系中Zw=0的平面上，将棋盘格上的某个角点设置为原点，理论上只要知道棋盘格每一个格子占据的尺寸，就能得出所有棋盘格内角点的世界坐标。同时棋盘格内角点的像素坐标可以通过图像处理的方法计算得出，从而借助于平面单应性、非线性优化等理论求解出相机的内外参数，相机标定后得到了内参和外参进而得到了物点和像点间的映射关系，所得参数如表1所示。表中参数A表示相机的内部参数矩阵；fx、fy为像平面中的有效焦距，u0、v0为图像的主点坐标，γ为相机的坐标轴之间的不垂直因子；k1、k2、k3、p1、p2为径向、切向畸变参数；矩阵R和矩阵T为相机的旋转矩阵和平移变量，表示相机左目坐标系转换到相机右目坐标系的旋转矩阵和平移向量。

表1 相机标定的参数

本质上来说双目立体视觉，是相机左目和右目再看同一个目标点时，连接探测器上的像点和相机投影中心进行反投影，两条光纤的交点位置实际就是目标的位置。

2.2 机械臂末端执行器坐标系与基座坐标系的转换

机械臂运动的姿态一般是XYZ三轴旋转方向，欧拉旋转变化矩阵是由3个非交换的旋转矩阵相乘计算，旋转次序不同共分为12种不同类型的欧拉角。该机械臂末端执行器坐标系与基座的坐标系转换的欧拉角顺序为ZYX型，转换的关系用旋转矩阵R zyx(α,β,γ)表示，转换示意图如图4所示。

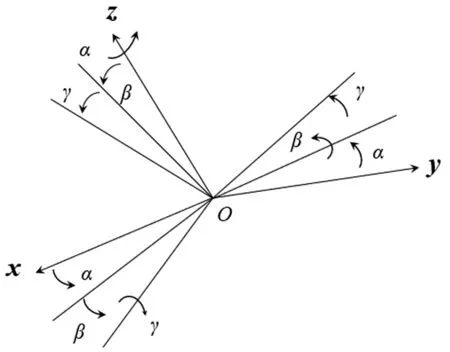
图4 欧拉角旋转示意图

图4所示为机械臂末端执行器坐标系先绕着z轴旋转α角，再绕y轴旋转β角，最后绕x轴旋转γ角，得到了基座的坐标系，转换公式为：

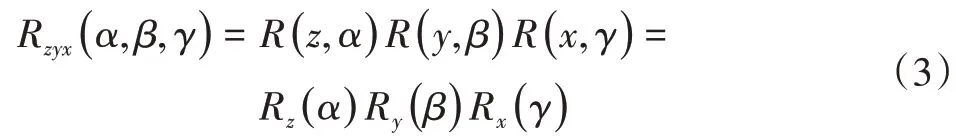
由式（3）可计算出机械臂末端执行器坐标系和基座坐标系旋转矩阵的结果：

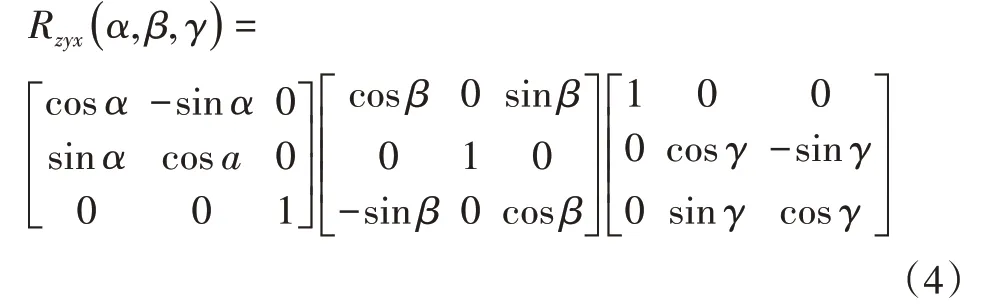
通过式（4）可知手眼相机标定前需要知道机器人坐标系旋转矩阵的旋转顺序。

2.3 手眼相机精度测试坐标转换关系

坐标系转换关系如图5所示。坐标系转换用4×4矩阵描述，欧拉角采用ZYX顺序，即旋转矩阵R=rotz×roty×rotx。箭头指向标识源坐标系与目的坐标系，X为法兰坐标系和目标外部基准坐标系转换关系，T1为关节测量臂测量目标及其工装外部基准转换关系，T2为相机外参，相机与相机外部基准转换关系，T3(n)为相机输出位姿，T4(0)为初始相机外部基准坐标系与目标外部基准坐标系转换关系，T4(n)为相机外部基准坐标系与位移后目标外部基准坐标系转换关系，T3'(n)为通过下式解算出相机测量目标位姿真值。

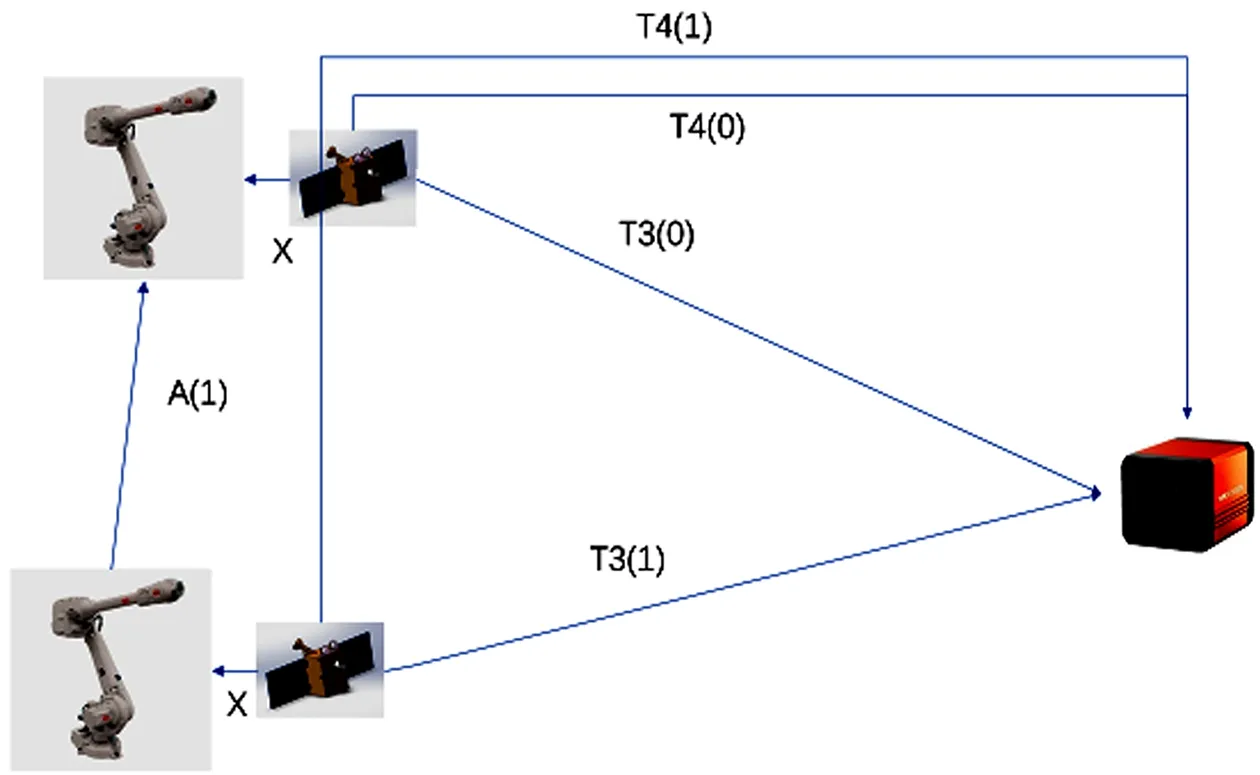
图5 手眼相机关系转换

以初始点为外部基准，运用Matlab随机生成ABB运动轨迹，轨迹文件记录轨迹点与初始点六自由度偏差A（n），上位机控制机械臂逐点运动并记录输出位姿T3作为测量值，外参T2作为已知量，根据下式子求解T3'(n)；

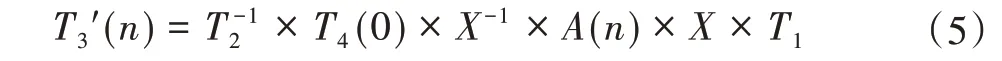
3 软件设计实现

在vs2017作为上位机软件开发平台，结合C++与其他的库函数进行控制程序的二次开发，界面如图6所示。运用张正友标定法选用5×5的圆点标定板作为校准物体，选用圆形标定板是因为圆的确定相对精准，可以使用圆外围的像素减少了图像噪声的影响。标定板上25个已知特征点如图7所示，可以采用最小二乘法求解降低误差的影响。本实验搭建了自动化标定平台，将机械臂末端法兰上采集的标定板图像输入到上位机软件中进行计算，由图所示可以获得相机的内参数和外参数，为后续精度测试提供保障工作。

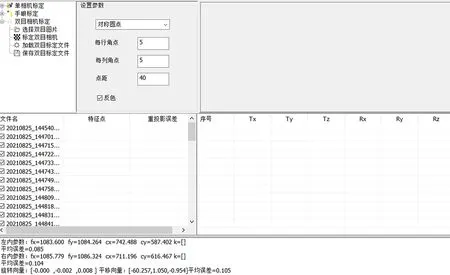
图6 标定MFC界面

图7 标定板

4 实验结果及分析

手眼相机测量精度前的标定的本质是AX=XB的求解过程，在实际的应用中，A和B都会不可避免的存在误差。对于本文研究的手眼系统，A的误差表示机械臂的相对运动误差，B的误差表示相机运动的估计误差，影响手眼相机标定方法的精度。所搭建的手眼相机自动化标定平台测试精度结果如表2所示，RMS表示均方根，公式不再赘述。

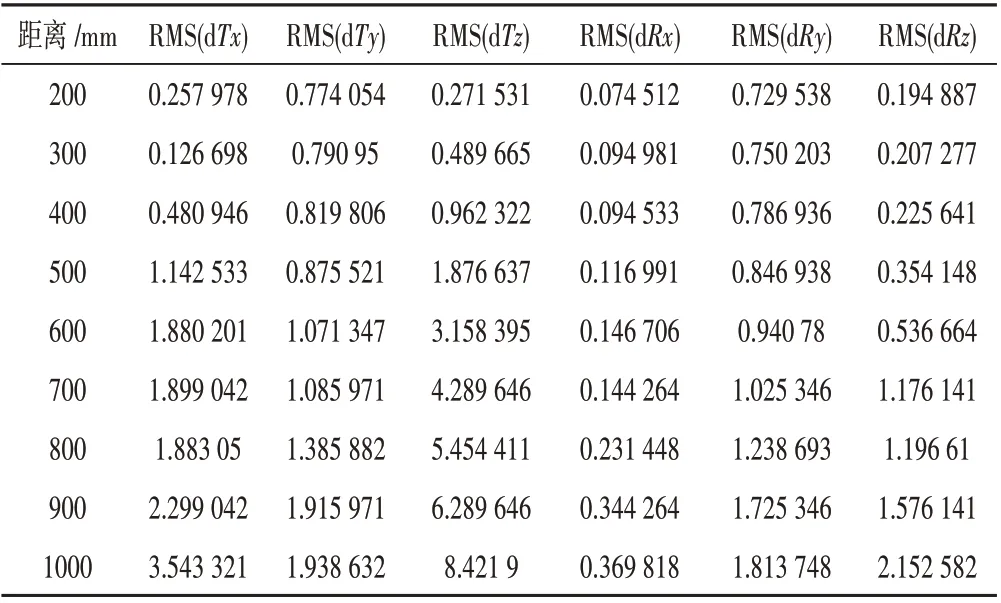
表2 双目精度测试结果

为验证标定的精度，将标定的结果代入相机模型进行误差分析得到了如图8～9的误差分布曲线。

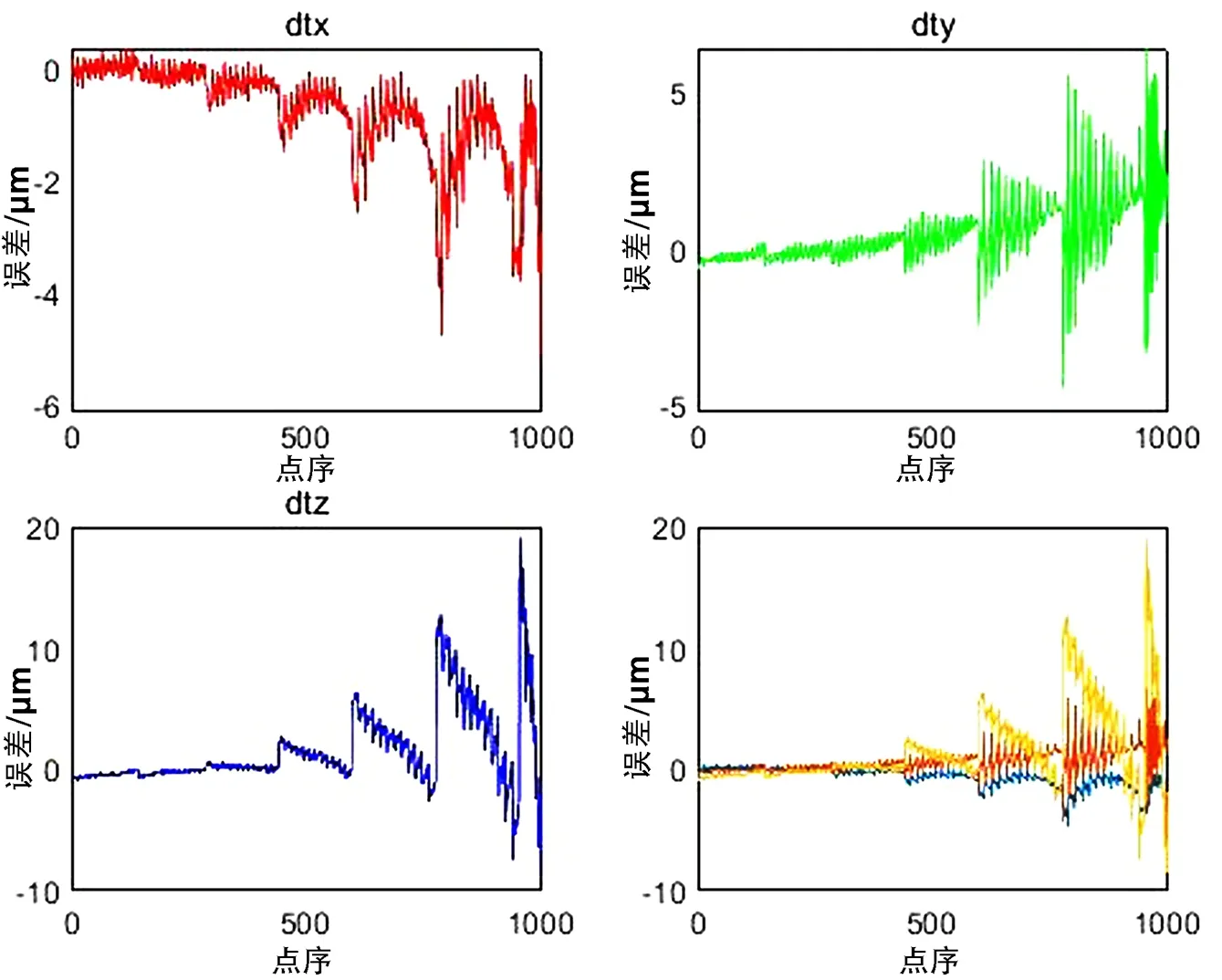
图8 双目平移误差

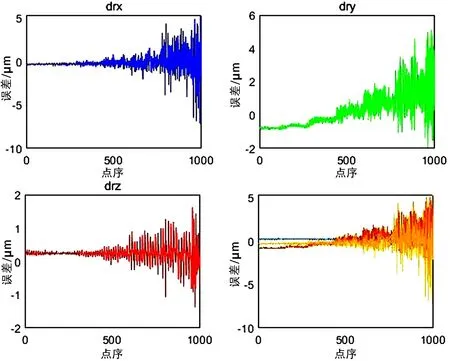
图9 双目角度误差

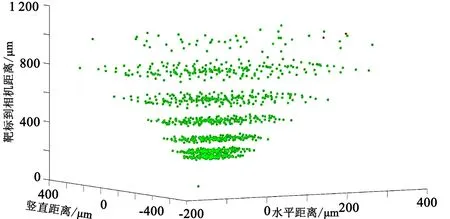
图10 双目测试点三维分布（绿色点不超差、红色点超差）

5 自动化标定平台的不确定度分析

手眼相机自动化精度测量存在不确定误差，由于关节测量臂定位误差23μm，工业机器人重复定位误差15μm，在标定过程中标定板不可避免会存在1个像素的误差。因此用不确定度μc来评估系统误差，由下式各个不确定度分量合成，μ1表示关节测量臂误差，μ2表示机械臂误差：

由式（6）可算自动化平台的不确定度误差约为27.5μm，由此可知自动化测试平台的精度高，试验的重复性良好，满足了测量精度的要求，满足实际的使用需求。

6 结束语

本文根据机器视觉高精度应用要求，在实际应用的手眼相机中，搭建了一套自动化精度测试平台，开发出兼顾精度和低人力成本的双目自动化精度测量平台，从实验中对位姿测量精度进行验证，对手眼相机系统进行标定试验并验证视觉定位的精度分析，实验结果表明，在此平台下手眼相机系统定位精度达到了27.5μm，且解放双手，通过上位机之间的相互通讯减少人为操作，此平台具有较高精度及稳定性，满足实际航空航天的应用需求，具有很大的实际使用价值。