磨损形貌特征对套管承载性能影响的有限元分析

满振峰，窦益华※，秦彦斌，刘君林，万志国

（1.西安石油大学机械工程学院，西安 710065；2.青海油田钻采工艺研究院，甘肃酒泉 736200）

0 引言

随着石油工业的发展，开采难度的增加导致复杂井数量与日俱增，高难度复杂井作业周期长、摩阻大、套管所受的侧向力大，因此套管磨损现象十分严重，威胁着井筒的完整性。如新851井技术套管多处严重磨损，套管对内压载荷的承载能力降低，在高压气体作用下技术套管破裂，最终封井。套管磨损问题已成为制约油气井安全高效生产及经济效益不可忽视的影响因素。

因此，国内外许多学者对套管磨损问题进行了研究。叶翠莲等[1]基于ABAQUS软件在套管塑性变形分析时引入屈曲特征值，建立了磨损套管的剩余强度分析方法。金春玉等[2]建立了弯曲套管力学模型，研究了复合磨损对套管抗挤强度的影响，研究表明套管抗挤强度与弯曲曲率呈负相关关系。谭雷川等[3]基于几何关系和能量耗散原理，建立了考虑钻柱正弦屈曲的套管磨损预测模型，该模型应用于涪陵页岩气套管磨损预测。刘书杰等[4]基于White和Dawson的“磨损-效率”模型，建立了大位移井况下套管月牙形磨损缺陷深度的计算模型，提供了大位移井中套管磨损的预测方案。连吉弘[5]、高德利等[6]基于动态的套管磨损累积特征及能量原理，建立了预测月牙形磨损缺陷深度的非线性模型。孙连忠等[7]基于套管全尺寸磨损试验，研究了接头尺寸和磨损时间对磨损因子的影响规律，其研究结果表明非线性模型[6]中随磨损缺陷宽度和深度的增大磨损因子减小。Kuma等[8]考虑井眼曲率和挠率对套管磨损的影响，并通过“比能”修正了套管磨损因子，提出了“磨损-能量”模型。宋学锋等[9]基于Bradly的磨损模型[10]研究了油管滑动诱导套管产生的磨损，且通过数值方法分析了磨损缺陷影响套管应力分布的规律。窦益华[11]、王小增等[12]针对套管磨损缺陷深度及剩余强度分析，基于双极坐标系法建立了套管磨损深度的计算模型，研究了月牙形磨损套管承载性能。正常钻、修井作业过程中不可避免都会对套管造成磨损，且连续性接触是造成套管磨损的主要因素，套管磨损形式主要表现为“月牙形”、“偏心筒”形式。因此，本文采用有限元方法建立了不同形貌特征月牙形磨损套管的有限元模型，并引入应力集中比值的概念，研究月牙形磨损缺陷的形貌特征对套管安全性的影响规律。本文研究可为现场应用及套管安全性评价提供一定参考。

1 三维有限元模型建立

1.1 几何模型

在油气井生产作业过程中，由于狗腿度、钻具组合等因素作用，钻杆接头及钻杆本体与套管发生连续性接触，使得套管发生偏磨，对套管造成月牙形磨损。本文采用SolidWorks软件建立产生月牙形磨损后套管三维模型，如图1所示。

图1 磨损套管

本文中“月牙形”磨损套管模型的磨损量采用偏磨率ε来度量，偏磨率为套管壁厚最大磨损量与套管初始壁厚的比值，如图2所示，其公式为：

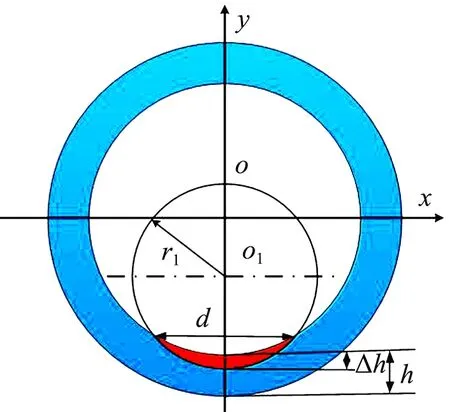
图2 月牙形磨损缺陷示意图

式中：Δh为套管壁厚最大磨损量；h为套管初始壁厚。

1.2 套管有限元模型

实际工况下套管处于高温高压作用，而高温环境和内部压力会对套管的材料参数和力学性能产生影响。同时考虑到套管生产制造过程中初始的性能缺陷，为便于模型建立和计算，本文做以下假设[7-12]：

（1）不考虑套管的壁厚不均度及不圆度等初始制造缺陷的影响；

（2）不考虑热力学效应与化学协同作用的影响；

（3）磨损前后套管材料是各向同性的均匀弹性体，始终处于小变形范畴；

（4）考虑套管无限长，故忽略实际工况下套管残余应力的影响。

本文所建立的三维磨损套管模型，套管钢级选用P110，套管外径为177.8 mm，套管原始壁厚为12.65 mm，套管总长度采用300 mm，模型的材料参数如表1所示。

表1 材料参数

套管磨损前承受载荷作用属于对称问题，套管产生磨损缺陷后由于磨损缺陷不具有对称性，故磨损套管承受载荷作用不属于对称问题，未磨损套管为偏磨率ε=0的情况，为了更好地与磨损后套管承受载荷作用下应力情况形成对比同时避免对称约束导致的应变、应力情况不够真实，故本文未对建立的未磨损套管模型作对称简化，而是建立完整的未磨损套管模型。

未磨损套管网格使用线性完全积分单元C3D8，整个模型划分六面体结构化网格，六面体结构化网格既可以提高模型计算的准确性，同时缩短计算时间，三维模型及网格划分如图3所示。

图3 三维模型及网格划分

本文套管模型未对称简化，为了限制应力奇异及刚体位移，需在套管模型上选一点施加3个坐标轴（X、Y、Z）方向的约束，使有限元模型计算更加准确。模型约束施加情况如图4所示。

图4 约束条件施加

1.3 磨损缺陷对套管承载性能影响的判定

磨损套管的失效主要为套管磨损区域的局部塑性失效，即认为磨损区域的von Mises应力达到屈服极限后，就判定为套管发生失效，因此前人的研究大多采用失效准则来判定磨损缺陷对套管承载性能的影响。套管产生磨损缺陷后会在磨损缺陷区产生应力集中现象，应力集中是磨损区域的局部塑性失效最直接的原因，本文引入应力集中比值α来表征磨损缺陷对套管承载性能的影响，应力集中比值α公式为：

式中：σ1为磨损套管最大Mises等效应力；σ2为未磨损套管最大Mises等效应力。

2 套管承载性能有限元仿真

2.1 未磨损套管分析

套管除受重力作用外，还需施加其他类型外载作用。本文主要研究套管受内压载荷及外压载荷两种受载情况下磨损缺陷对套管承载特性的影响规律。

未磨损套管受到10 MPa外压载荷作用时，计算所得应力云图如图5所示。

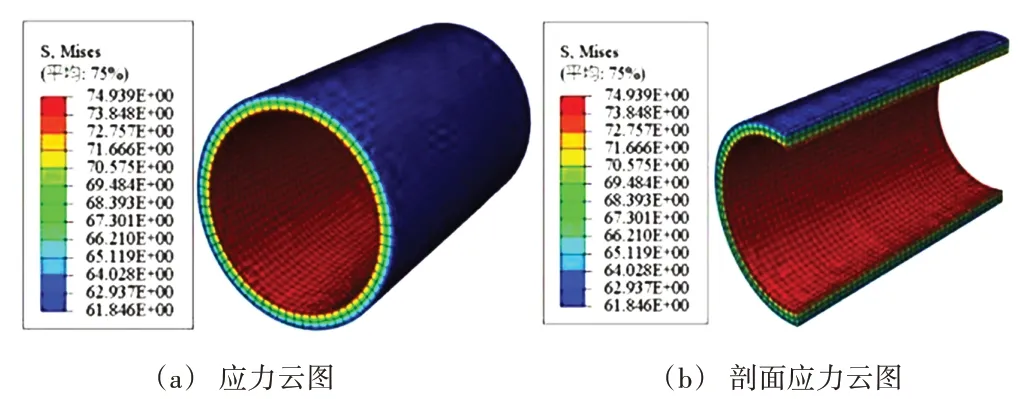
图5 未磨损套管受外压应力云图

从剖面应力云图可以发现，未磨损套管模型应力过渡较为均匀，即说明计算结果较为准确。通过计算得到的最大等效Mises应力74.939 MPa。

未磨损套管受到10 MPa内压载荷作用时，计算所得应力云图如图6所示。通过计算得到的最大等效Mises应力70.184 MPa。

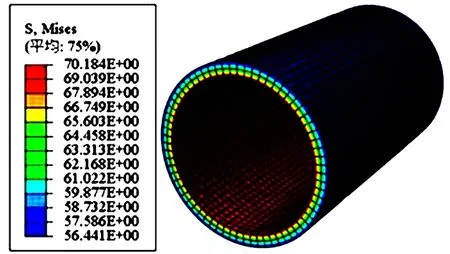
图6 未磨损套管受内压应力云图

2.2 偏磨率对套管承载性能的影响分析

由于狗腿度、钻具组合等原因油气生产作业过程中不可避免地对套管造成月牙形磨损，而月牙形磨损缺陷的形貌特征不同（图7）对套管承载性能的影响可能不同，即由于狗腿度、钻杆接头尺寸不同等原因导致磨损缺陷的偏磨率、开口大小不同进而对套管承载性能的影响不同，因此本文建立了具有不用偏磨率、不同开口大小磨损缺陷的套管有限元模型，研究其对套管承载性能影响规律。

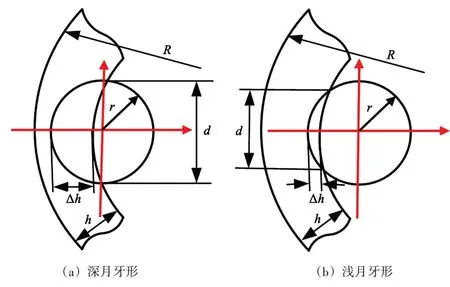
图7 不同形貌特征磨损缺陷

令月牙形磨损缺陷开口大小d固定，取不同的偏磨率ε，得到该条件下应力集中比值α，从而分析月牙形磨损缺陷的深度（偏磨率ε）对套管承载的影响。考虑到实际工况下套管壁厚最大磨损量小于50%，偏磨率ε取10%、20%、30%、40%，取偏磨率20%时磨损套管受到10 MPa外压及内压载荷作用时的应力云图如图8所示。由图可知，磨损套管模型受外压及内压载荷作用时在月牙形磨损区域附近出现了应力集中。

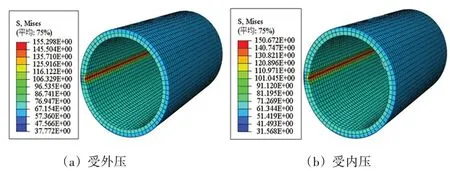
图8 偏磨率20%时受载荷应力云图

由仿真计算结果可得应力集中比值随偏磨率ε变化的规律如图9所示。由图可知磨损缺陷开口大小d固定，改变偏磨率的值，对套管模型施加外压、内压载荷作用时，随着偏磨率逐渐增大，应力集中比值逐渐增大，即应力集中情况加剧。因此可得缺陷开口大小d固定，随着磨损缺陷偏磨率增大磨损套管对外压和内压载荷的承载能力降低。

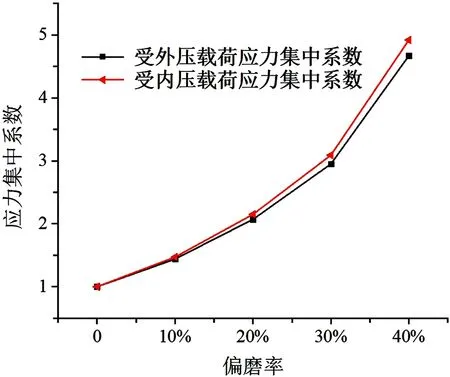
图9 应力集中比值随偏磨率变化

2.3 开口大小对套管承载性能的影响分析

令月牙形磨损缺陷∆h固定，改变开口大小d的值，得到该条件下应力集中比值α，从而分析月牙形磨损缺陷的开口大小对套管承载性能的影响。开口大小取10 mm、20 mm、30 mm、40 mm，开口大小取20 mm时磨损套管受到10 MPa外压及内压载荷作用，应力云图如图10所示。

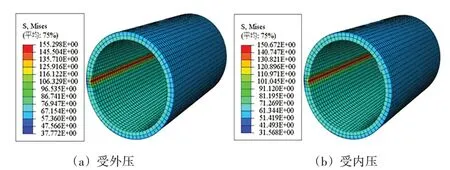
图10 开口20 mm时受载荷应力云图

由仿真计算结果可得应力集中比值随磨损缺陷开后大小d变化的规律如图11所示。由图可知缺陷∆h固定，改变开口大小d的值，对套管模型施加外压、内压载荷作用时，随着磨损缺陷开口大小逐渐增大，应力集中比值逐渐减小，即应力集中情况减缓。因此可得磨损缺陷∆h固定，随着磨损缺陷开口大小d的减小磨损套管对外压和内压载荷的承载能力降低。

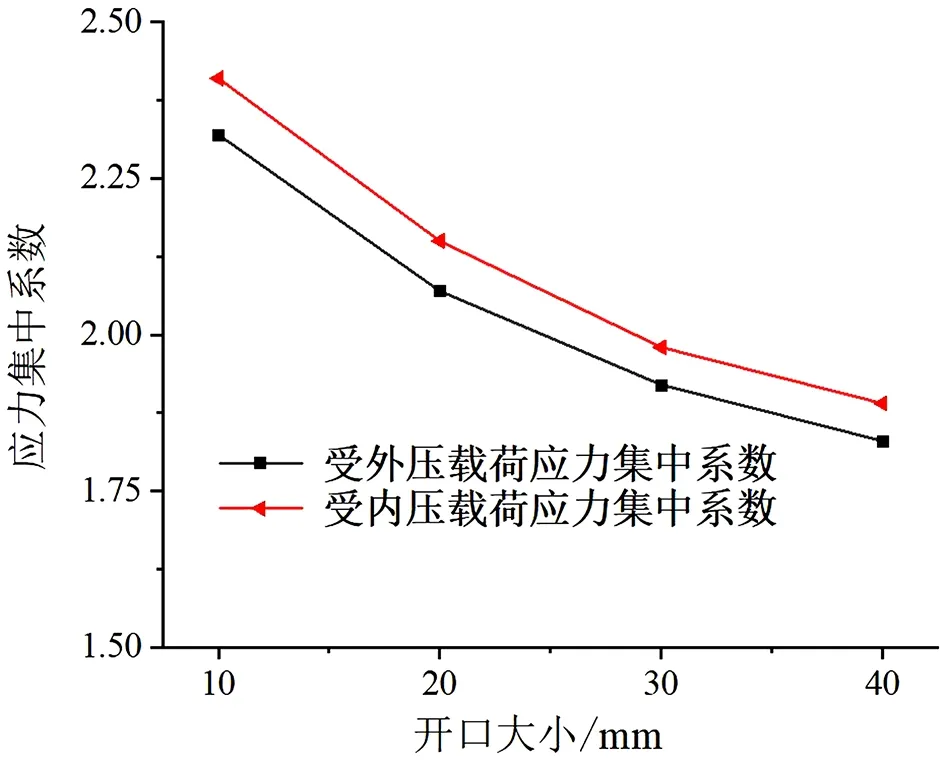
图11 应力集中比值随开口大小变化

2.4 缺陷数量对套管承载性能的影响分析

在实际钻、修井作业过程中随着作业工况的变化，钻杆本体、钻杆接头与套管的接触位置会发生变化即磨损点的位置会改变，从而会对套管造成不止一处的磨损如图12所示，因此磨损缺陷的数量也是影响套管承载性能的因素之一，本文针对月牙形磨损缺陷数量分别为1、2、3、4、5五种情况进行研究，选择磨损缺陷偏磨率10%，开口大小d=20 mm进行建模，载荷情况同样选择受内压作用10 MPa和受外压作用10 MPa的两种情况。得到各磨损缺陷数量情况下的应力集中比值，从而分析磨损缺陷的数量对套管承载性能的影响规律。

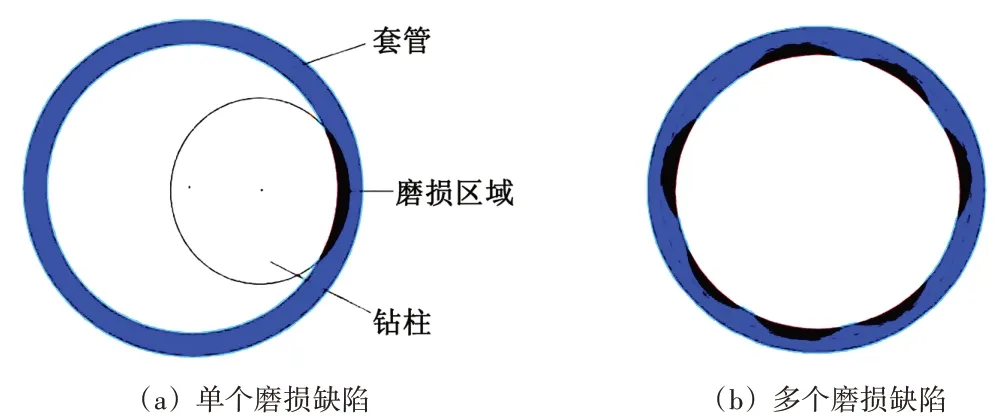
图12 磨损缺陷数量示意图

取偏磨率ε=10%开后大小为20 mm，磨损缺陷数量为2、3、4、5，磨损缺陷数量为4时磨损套管受到10 MPa外压及内压载荷作用时的应力云图如图13所示。

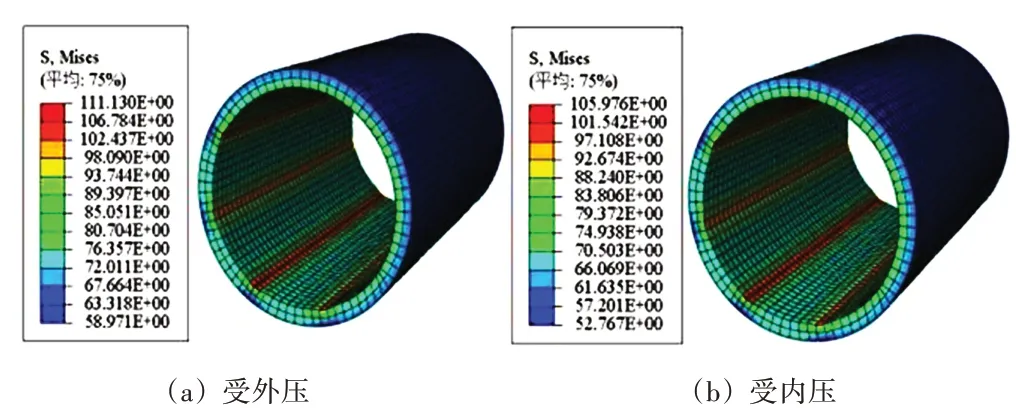
图13 磨损套管受外压应力云图

由仿真计算结果可得应力集中比值随磨损缺陷数量变化的规律如图14所示。由图可知取磨损缺陷偏磨率10%，开口大小d=20 mm，且假设磨损缺陷都处于套管的同一个截面位置上，磨损缺陷之间无交叉重叠，随着磨损缺陷数量的增多，对套管模型施加内压、外压载荷作用时，应力集中比值变化较小，即应力集中情况变化不明显。因此可得磨损套管承受外压和内压载荷作用时对缺陷数量的变化不敏感。

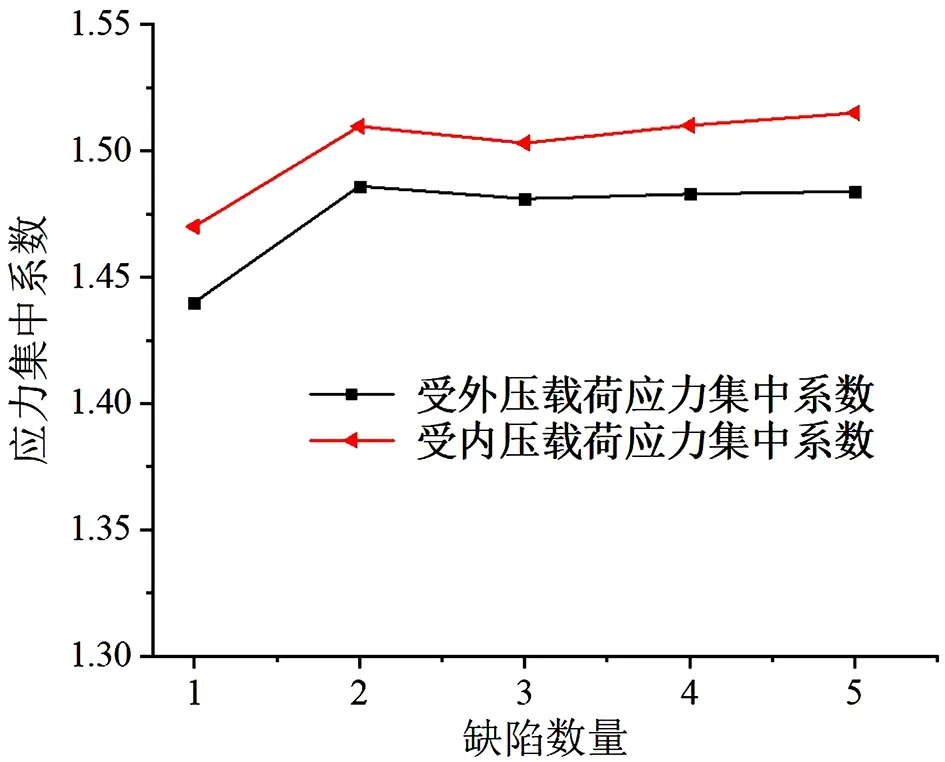
图14 应力集中比值随缺陷数量变化

3 结束语

为研究月牙形磨损缺陷对套管承载性能的影响规律，本文应用ABAQUS软件建立了未磨损套管及不同磨损程度套管三维有限元模型，并施加10 MPa外压载荷和10 MPa内压载荷作用，通过引入应力集中比值研究了磨损缺陷的偏磨率、开口大小及磨损缺陷数量对套管承载性能的影响，得到如下结论。

（1）内压载荷和外压载荷作用下不同形貌特征的月牙形磨损缺陷周围都会产生应力集中，应力集中程度越剧烈，套管承载能力越低。

（2）内压载荷和外压载荷作用下，偏磨率与应力集中比值呈正相关关系，即随着偏磨率增大，套管对外压和内压载荷的承载能力下降。开口大小与应力集中比值呈负相关关系，即磨损缺陷开口大小越小，套管对外压和内压载荷的承载能力越低。

（3）假设磨损缺陷都处于套管的同一个截面位置上，且缺陷之间无交叉重叠，随着磨损缺陷数量的增多，应力集中比值波动幅度较小，应力集中情况变化不明显，即套管承载能力对缺陷数量的变化不敏感。