车载动中通天线跟踪技术的研究

潘良勇 沈桂鹏 陆海帆

（南京熊猫汉达科技有限公司，江苏 南京 210000）

当前，卫星通信被全球广泛使用，这种通信方式相较于短波通信，一是通信质量高，受低频信号干扰小；二是通信距离远，范围广；三是系统容量大，易扩展，灵活性高等等，这些特点也使得卫星通信系统的整体性能必须严苛、可靠。

“静中通”系统，安装位置固定。在安装后，通过手动或者自动控制天线方位轴、俯仰轴、极化轴转动到指定位置，捕获卫星信标信号后，就可以长期稳定对准卫星并通信。目前在某些固定站、大型“动中通”系统，即安装在舰船、汽车、飞机等移动载体上的天线设备在运动过程中能够稳定跟踪，并实时、稳定地传输多媒体信息。目前广泛运用于各类军用场合、民用场合[3]。不同的场合，受地理位置、环境影响，收到的扰动也各不相同。为保证天线始终指向卫星，天线控制必须满足相当高的精度，才能确保天线稳定捕获信标信号。

在目前的车载动中通天线中，跟踪精度指标尤为重要，是影响动中通通讯性能的关键指标。目前跟踪精度包括导航信息测量精度、天线角测量精度、天线角度跟踪精度三个方面。

1 天线控制精度分析

1.1 天线角度测量精度

天线角度测量精度作为影响天线跟踪精度的重要因素，测量传感器选型尤为重要。本文选用高分辨率正交光电式编码器作为角度测量传感器，光电式编码器凭借自身体积小、精度高、无接触无磨损和抗干扰能力强等特点被广泛应用于各种高精度测量场合。

编码器中，光电转盘转动时，光敏元件产生A、B 相，相差90°的脉冲，并且根据两相的相位差得知转动方向，依据脉冲数得知转动位置。

1.2 天线角度跟踪精度

良好的角度跟踪精度离不开高性能的执行机构和优质且匹配的跟踪算法。

传统天线一般选用步进电机作为传动的执行器件，但是步进电机普遍存在高转速下扭矩急剧减小和低速共振等缺点。所以本方案放弃了传统步进电机方案，选用高性能直流无刷伺服电机，相比之下，直流无刷伺服电机具有扭矩不随转速升高下降和低速运转更稳定等明显优点。

在跟踪算法方面，可采用陀螺、角度解算和卫星信号三级反馈稳定跟踪技术。首先利用导航信息中陀螺角速率反馈信号进行前馈控制，确保系统的及时性；其次使用卫星信息和导航相关信息完成天线指向角度解算，通过对比各轴解算角度与当前时刻的实际角度进行二级反馈，确保天线指向角的准确性；最后将卫星信号引入闭环控制系统，用于三级反馈确保天线指向角始终处于信号最大位置，再次确保指向精度，可在导航信息准确性下降的情况下保证系统工作的稳定性及可靠性。

1.3 导航信息测量精度

传统动中通天线，天线导航信息测量一般采用内部BD/INS 组合导航方案，但对于要求重量轻、体积小的小孔径天线则无法选用较大型的高精度惯导，因此普遍存在姿态测量精度低，航向漂移等问题。

鉴于上述原因，本天线采用车载高精度导航系统作为导航信息输入源，有效解决了姿态测量精度低和航向漂移等问题。但是由于引入了外部车载导航系统，车载导航坐标系可能与天线坐标系存在一定的安装偏差，需要再通过算法对安装偏差进行补偿，使导航信息转换到天线坐标系后无限接近于真实测量值。

1.4 快速对星和遮挡恢复设计分析

对星时间表征为天线由待机状态转入稳定跟踪状态需要的时间。本项目使用天线自带惯导，惯导对准后，天线根据接收到的对星信息迅速解算出需要转动的方位角、俯仰角和极化角，为达到对星时间最短，控制系统会同时驱动方位电机、俯仰电机和极化电机以各自最大速度和加速度进行高速响应，使三轴以最短时间到达指定位置。

遮挡恢复指标主要考验天线在没有信标闭环条件下导航信息的测量精度。一般情况下，遮挡存在部分遮挡和完全遮挡两种。部分遮挡时，如树木、矮小建筑物遮挡，时间短，当发现AGC 值低于阈值且不为0 时，判定存在部分遮挡情况，停止圆锥跟踪；信号超过时，启动圆锥跟踪，这样操作可以最大限度避免遮挡干扰导致的错误调整，影响跟踪。完全遮挡时，控制器界面上AGC 值为0，通信中断，时间较长时，则进入纯粹依赖惯导的跟踪阶段[4]。

本文中天线导航信息由天线高精度导航系统提供，天线通讯链路中断并不会对车载导航系统产生影响，此时天线控制系统会进入陀螺加角度解算的二级反馈稳定跟踪状态，一旦链路恢复天线可在极短时间内完成信号重捕获，重新进入陀螺、角度解算和卫星信号三级反馈稳定跟踪状态，并通过卫星信号闭环使信号达到最大[6]。

2 天线测姿方案

从系统上电开始到天线稳定锁定卫星、数据建链成功的时间，是系统成败的关键因素之一。为实现天线快速准确对星，需要获取较为精确的横滚角、俯仰角、方位角，代入姿态解算矩阵，得出天线实际的指向角。而在实践中，俯仰与横滚角度值均较小，在模型推导中影响不大，方位角的可靠性和精度尤为重要。

定向测姿有惯性导航、卫星导航，以及组合测姿，各有优缺点和应用环境，需要用户根据实际情况决定[1]。为保证测姿准确性，本文提出采用组合测姿方式，优势互补，并信息融合、滤波的解决方案。推导出状态误差模型与信息融合模型，提高系统估算精度。

组合测姿系统的原始数据来源为两个部分，卫星导航系统的速度位置测量值和惯性仪表的测量值。惯性仪表的原始数据频率高，也包含了随机噪声，通常为高频部分[2]。利用小波降噪的方法将其减小，将惯性仪表的初始值通过小波变换整理，获得对应的小波系数，在通过选择合适的阈值，筛选出原始信号对应的小波系数，同时将噪声对应的系数减小，这样原始信号就得到了保留而噪声信号就得到了消除。再将所有数据信息小波逆变换，从而获得去噪效果明显的信号[7]。

2.1 状态误差模型建立

搭建惯性和卫星组合的高精度测量系统需设计状态误差模型。考虑到工程实践中容易实现且适合产品的大批量生产，选用速度组合模式。此模式结构较简单，且运算量要求低，还可提高系统的可靠性，增强了系统冗余度。当北斗和惯导系统中的任何一种失效时，组合系统仍然可以继续提供姿态信息，从而保证了系统姿态测量的连续性。因此选择5 维状态变量的误差方程和2 维速度的观测方程。具体如下所示：

2.1.1 选择速度误差和姿态误差作为状态变量，如下所示：

2.2 卡尔曼滤波算法数据融合

一般来说，惯性导航存在误差，如零偏、敏感轴失调角偏差等等，对正常测姿有干扰。选用卡尔曼滤波算法将二者的测量信息进行数据融合，解算出姿态误差值。Kalman 计算过程包括滤波计算和增益计算两个回路，如图1 所示。

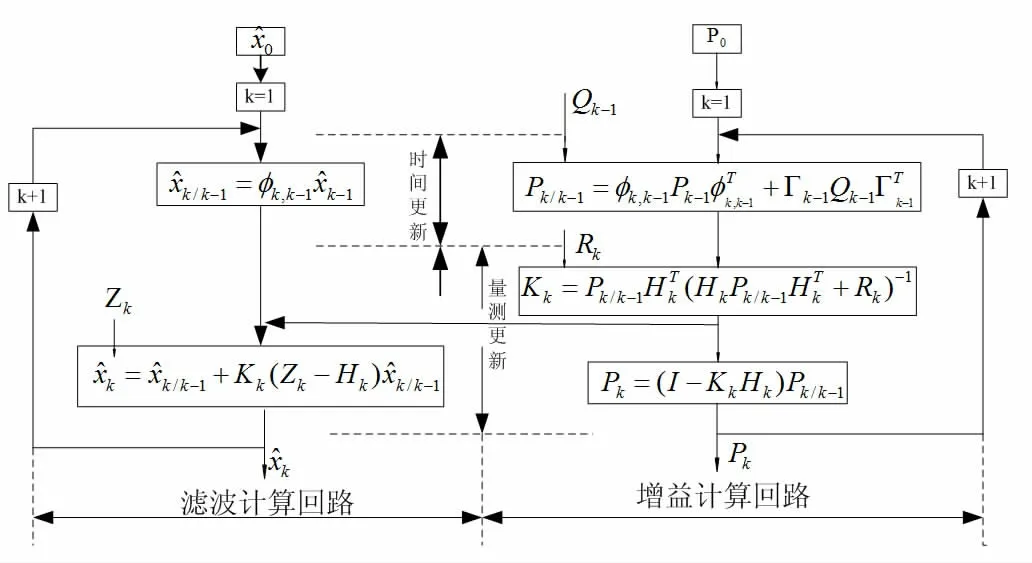
图1 卡尔曼滤波的两个计算回路

滤波选择合适的估计误差方差阵P、观测误差方差阵R 及状态误差方差阵Q，组合周期选取为1s，估计出姿态误差的大小。

误差补偿校正有两种：开环校正、闭环校正。对惯性解算出的姿态需要进行误差补偿校正，如图2 所示，获得高精度的姿态值。选择输出校正应依据设计的系统而定，根据本系统的特点，选择反馈校正方式。

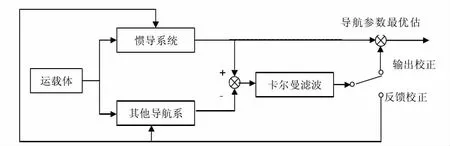
图2 卡尔曼滤波的两个计算回路

卡尔曼滤波算法解算过程中，误差方差阵的参数调节大大影响着误差值的估计效果。误差方差阵包括估计误差方差阵P、观测误差方差阵R 及状态误差方差阵Q，P 阵是随系统实时变化的，Q 阵属于系统误差阵，因设计的系统模型而定，R 阵取决于观测量的统计误差即北斗系统的速度观测量误差。一般情况下，R 阵可选用定值用于整个系统，考虑到北斗的量测误差在不同的路况如上下坡、转弯、遮挡等环境下的误差值是变化的，因此可根据实时测量值来估计此阵，达到自适应调节的目的，进而可提高系统的估计精度，如图3 所示。

图3 惯性卫星组合导航系统框图

通过对惯导、卫星导航、组合导航的航向角信息的仿真解算，取一定时间段内的数值，并辅以图形化处理，最终得到图4 所示的航向角误差曲线图。

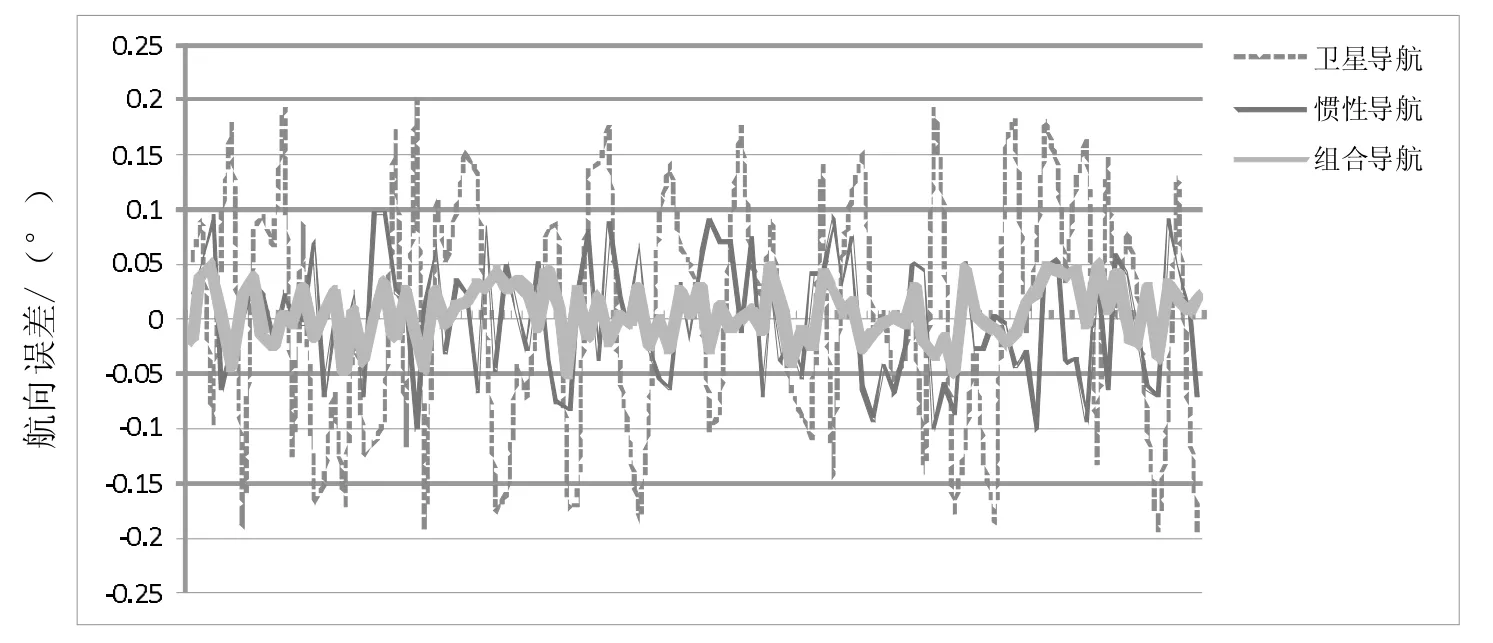
图4 航向角误差图

从误差图可以明显看出，单单使用卫星导航数据，航向角精度在0.4°左右；使用惯性导航时，航向角精度在0.2 度左右；使用组合导航时，精度约在0.1 度。数据分析表明，组合测姿算法更能有效提高测姿精度。

通过地理系下的卫星指向角可生成天线系(a 系)与地理系（n 系）之间的坐标转换矩阵，加上组合导航系统提供的融合后的姿态及航向信息可生成载体系与地理系之间的转换矩阵，由二者即可得到载体系与天线系之间的转换矩阵，根据载体系与天线系通过天线转台方位、俯仰和极化三轴的转动关系，即可求得天线对应的方位、俯仰及极化转动指令角，从而得到精准的指向精度。

3 结论

跟踪精度是影响动中通通讯性能的关键指标。而导航信息中的航向角在卫星通信天线稳定跟踪、动态开通等功能上极其重要。采用单惯导方案时，无法克服零偏、发散；使用卫星导航，连续性差，可靠性不足；采用组合测姿时，建立模型，并将惯导数据和卫星导航数据融合滤波，得到较为精确的姿态数据，精度提高两倍以上。因此，采用此种组合测姿结果可靠。由此经过矩阵转换，产生方位轴、俯仰轴、极化轴准确的指向角，从而可以大大提升天线跟踪精度。