基于最大信息系数和多目标Stacking集成学习的综合能源系统多元负荷预测

崔树银，汪昕杰

（上海电力大学 经济与管理学院，上海 200090）

0 引言

能源是人类社会发展的关键因素。据预测，2030年能源需求将增长50%以上［1］。在传统能源子系统单一运行模式下，电、热、冷等能源之间无法得到充分转化，导致能源利用效率低下以及清洁能源无法被充分消纳等［2］。因此，综合能源系统IES（In-tegrated Energy System）和能源互联网EI（Energy Internet）被相继提出。IES 作为EI的物理载体，包含电力供应、热力供应、天然气供应等［3］。多元负荷预测的精度直接关系到IES 的能源调度和运行规划是否合理有效。传统负荷预测只需考虑单一能源负荷，而IES 负荷预测需综合考虑电、热、冷等多类型能源之间的耦合关联，使得IES 多元负荷预测的难度增大。

目前，针对传统单一能源子系统负荷预测研究已取得较好的研究成果，例如：在传统的电力负荷预测方面，文献［4］考虑天气条件、电价、日历信息和历史负荷数据，采用联合概率密度方法进行预测；在热负荷预测方面，文献［5］将灰狼优化算法和差分进化相结合来对支持向量机进行优化，该预测方法同样适用于换热站和热源；在冷负荷预测方面，文献［6］针对冰蓄冷空调中冷负荷预测存在数据关联度低的情况，提出了一种组合神经网络模型来解决这一问题。

相较于单一负荷预测，IES多元负荷预测相关研究仍处于初级阶段。近年来，机器学习等人工智能技术广泛应用于负荷预测领域，针对IES 多元负荷间复杂的耦合关系，无需建立准确的数学模型，仅通过非线性映射分层学习就能得到数据之间的关系。文献［7］利用混沌理论进行变量空间重构，并采用卡尔曼滤波对电、热、冷负荷进行预测；文献［8］将多任务学习和长短时记忆网络相结合，通过共享层来模拟各能源子系统负荷之间的耦合特性；文献［9］通过构建深度结构的多任务学习模型，考虑热、电、气之间的耦合性，建立了“离线+在线”的预测模式；文献［10］基于多层径向基函数神经网络模型实现了电、气、热多元负荷预测；文献［11］利用核主成分分析法对原始数据进行降维，并分别用深度双向长短期记忆神经网络和多元线性回归模型进行多元负荷预测，然后对采用这2 个模型预测的结果进行重构得到最终结果。上述文献针对多元负荷预测大多采用单一预测模型或将几个模型相组合的方法。近年来，多模型融合算法在负荷预测领域取得了一定的成就，文献［12］在Stacking 集成学习框架下融合多个机器学习及深度学习算法，通过实际算例证明多模型融合算法相较于单一模型或简单的模型组合方法有着更高的预测精度。目前将多模型融合算法用于多元负荷预测领域的研究较少。因此，本文借助Stacking集成学习的思想，同时引入多目标回归来解决传统Stacking 集成学习模型无法进行多变量预测的问题。

综上，本文提出一种基于多目标Stacking 集成学习模型的多元负荷协同预测方法。首先，引入最大信息系数MIC（Maximal Information Coefficient）理论，对多元负荷及天气因素进行相关性分析；其次，引入负荷耦合形态指标，深度挖掘多元负荷间的耦合关系，并通过计算得到的MIC 值进行输入变量筛选；然后，将多目标回归的思想与Stacking 集成学习模型相结合，建立多元负荷协同预测模型；最后，通过实际算例验证所提模型的可行性。

1 多元负荷及天气因素相关性分析

IES是一个以电力系统为核心，具有各种信息化设备的能源平衡系统，可以实现电、热、冷、气的多能互补。具体的IES 交互图［13］如附录A 图A1 所示。从图中可以看出，IES各能源子系统之间可以通过某种能源转换装置进行能源二次利用。不同负荷之间能通过特定形式实现相互转换，表明了多元负荷之间存在复杂的耦合关系。因此，深度挖掘多元负荷之间的耦合特性，同时分析多元负荷及天气因素之间的相关性，这对于提高模型预测精度起到了重要的作用。

1.1 MIC

MIC［14］于2011 年首次被提出，不仅可以衡量2个变量之间是否存在线性关系，还可以观测变量间是否具有正弦性、周期性等非线性关系，而且MIC对于含有噪声的样本具有较好的鲁棒性。MIC 值的取值范围在0～1 之间，MIC 值越大，表明2 个变量间的关联程度越高。

MIC 的基本原理为：如果2 个变量之间存在相关性，则可以在由2 个变量组成的散点图上绘制网格，并利用互信息MI（Mutual Information）和网格划分来计算MIC。利用MIC 进行相关性分析的具体步骤如下。

1）设天气因素变量A={ai}(i=1，2，…，n)和多元负荷B={bj}(j=1，2，…，m)，其中n和m分别为天气因素和多元负荷变量的数量。即MI 值fMI(A，B)的计算公式为：

式中：B(δ)为关于δ的函数，设为δ0.6。

根据上述方法，对实际美国亚利桑那州立大学Tempe 校区的全年IES 数据及天气数据进行相关性分析。

1.2 多元负荷之间的相关性分析

在IES 内部中，不同能源之间可以通过某种特定的形式进行相互转化，这表明多元负荷之间存在一定的相关性。多元负荷曲线如附录A 图A2所示。从图中可以看出，电、冷负荷的曲线波动较为接近，都呈现“夏高冬低”的趋势，而热负荷曲线波动正好与之相反，呈现“夏低冬高”的趋势，这表明电、热、冷负荷之间有较强的季节互补性。为了更加直观地量化多元负荷之间的关系，选择采用MIC值来测量电、热、冷负荷间的关联程度。由于电、热、冷负荷的季节互补性，在不同季节电、热、冷负荷存在不同程度的相关性，其量化结果如表1所示。

表1 在不同季节多元负荷之间的MIC值Table 1 MIC values among multiple loads in different seasons

由表1 可知，在不同季节电、热、冷负荷之间的相关程度存在明显差异。本文将MIC 值大于0.3 的变量作为强相关变量，MIC 值小于0.1的变量作为弱相关变量。夏季电负荷与热负荷间的相关程度最低，而电负荷与冷负荷间的相关程度最高，而冬季与夏季正相反；春季和秋季的电、热、冷负荷间的MIC值均大于0.3，表明其具有较强的相关性。上述分析表明在进行多元负荷预测时，不能忽略负荷间的相关性。

1.3 多元负荷与天气因素的相关性分析

电、热、冷负荷除了受到负荷之间的相互耦合影响之外，对于天气因素也较为敏感。不同季节的天气因素对于电、热、冷负荷的影响程度不同。因此，深度挖掘电、热、冷负荷与天气因素之间的相关性，对提升模型的预测精度起到重要的作用，具体结果见附录A 表A1。从表中可知，不同季节的天气因素与多元负荷之间的相关程度存在明显差异。如在春季，温度与多元负荷间的MIC均大于0.3，具有较强的相关性，而降雨量与多元负荷间的MIC 均小于0.1，相关程度较弱。因此，根据附录A 表A1所示的季节差异性分析可知在不同季节应选取不同的天气因素作为输入变量。

1.4 负荷耦合形态指标的相关性分析

由于IES 特有的交互结构，其多元负荷间具有较强的耦合特性，深度挖掘其耦合关系对于提升模型的预测精度起到重要作用。因此，为了反映多元负荷间的耦合特性，提出电冷比、电热比、冷热比这3 个负荷耦合形态指标，以充分利用IES 多元负荷间的耦合信息来提升多元负荷协同预测的准确性。为了验证负荷耦合形态指标能增强多元负荷的可预测性，利用MIC 值来量化负荷耦合形态指标与多元负荷间的相关程度，结果如表2所示。

表2 负荷耦合形态指标与多元负荷间的MIC值Table 2 MIC values between load coupling morphological indexes and multiple loads

由表2 可知，负荷耦合形态指标与多元负荷间具有较强的相关性。在夏季，电冷比、冷热比与多元负荷间的相关程度较高，其中冷热比与冷负荷间的MIC 超过0.8；在冬季，冷热比、电热比与多元负荷间的相关程度较高，其中电热比与热负荷间的MIC 超过0.7。由此可知，负荷耦合形态指标可以很好地反映多元负荷间的耦合关系。因此，选取负荷耦合形态指标作为模型的输入变量来提升多元负荷协同预测的精度，具有一定的可行性。

2 基于多目标Stacking 集成学习的多元负荷协同预测模型

2.1 多目标回归

多目标回归［15］也可以被称为多变量预测和多输出回归。多目标回归是基于多标签分类的思想演化而来的，可以同时预测多个相互关联的连续型变量，通过深度挖掘多个输出变量之间的关联性来提升模型的预测精度。

多目标回归算法目前有堆叠单目标回归SST（Stacked Single-Target）算法和集成回归链ERC（Ensemble of Regressor Chains）算法这2 种。SST算法主要分为以下2 个阶段：第一阶段，针对每个输出变量，先进行单目标的回归预测；第二阶段，将第一阶段每个输出变量的预测值扩充至原始输入空间，组成新的输入变量，再输入同一个多目标回归模型进行多输出预测。ERC算法为每个输出变量建立一个单独的回归模型，与SST 算法不同的是，其在扩充原始输入空间时，采用的是对先前输出变量的实际值进行扩充，再随机生成多条回归链，每个输出变量基于链的不同位置得到其预测值，最后通过计算平均值得到最终的预测结果。

2.2 双向门控循环单元原理

双向门控循环单元BiGRU（Bidirectional Gated Recurrent Unit）［16］将具有相反传输方向的2 个隐藏层连接到同一输出层，以便于输出层从过去和将来的状态中获取信息。这意味着BiGRU 神经网络能够从2 个不同的数据方向学习信息，从而进行更准确的预测。BiGRU 的思路是将规则的GRU 神经元分为前向传播和后向传播。BiGRU 的结构如图1所示。

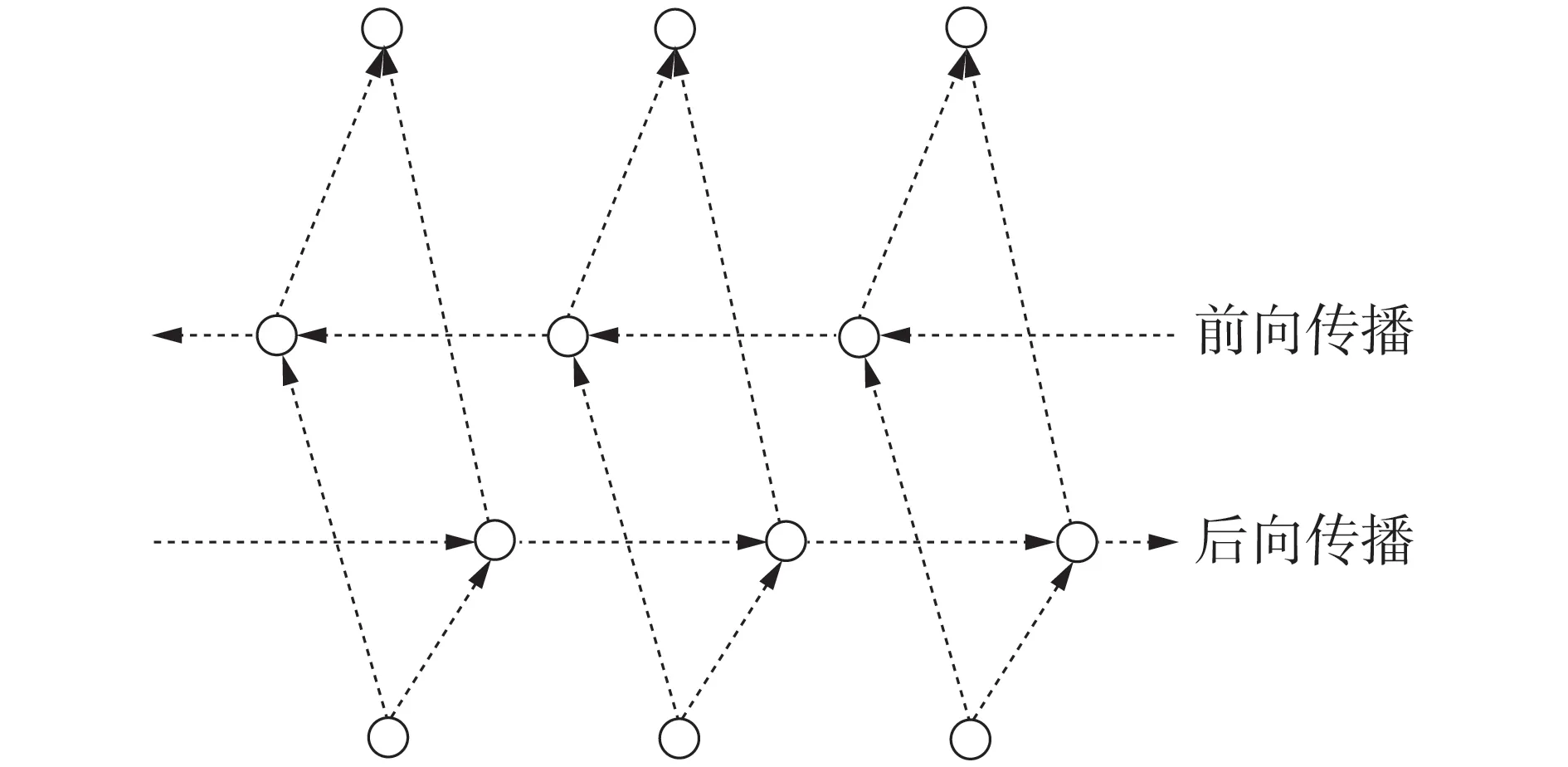
图1 BiGRU结构图Fig.1 Structure diagram of BiGRU

2.3 正则化贪心森林算法

正则化贪心森林RGF（Regularized Greedy Forest）算法［17］于2014 年被提出，目的是为了应对传统梯度提升决策树GBDT（Gradient Boosting Decision Tree）收敛速度较慢、容易过拟合等不足之处。RGF算法与GBDT 不同，在每次迭代时需对整个决策森林进行学习，并在新增树后对全局进行参数优化，同时引入正则项来防止过拟合现象。

2.4 多目标Stacking集成学习

传统Stacking 集成学习算法通过将不同的机器学习算法融合在一起，并通过K折交叉验证来进行基学习器训练集的划分，再将基学习器训练后得到的结果作为元学习器的输入，从而得到最终预测结果。具体预测流程如图2所示。

从图2中可以看出，传统Stacking 集成学习模型是对单一任务进行预测的，预测结果也是单一结果输出的。考虑到IES 特有的结构特性，电、热、冷负荷之间有较强的耦合关系，将多元负荷单独进行预测往往会忽略多元负荷之间的关联性，从而影响预测精度。针对这类问题，将多目标回归的思想融入Stacking集成学习模型中，充分考虑电、热、冷负荷之间的耦合性，从而进行多元负荷协同预测。多目标Stacking集成学习预测模型主要分为以下2个阶段。

图2 传统Stacking集成学习模型预测流程图Fig.2 Forecasting flowchart of traditional Stacking ensemble learning model

1）第一阶段：基于传统Stacking 集成学习模型的多元负荷单独预测。

在第一阶段中，仍使用传统Stacking 集成学习模型的基学习器与元学习器训练模式，对电、热、冷负荷分别进行预测。首先，采用5 折交叉验证划分训练集，并在第一层基学习器算法选取轻量级梯度提升机LightGBM（Light Gradient Boosting Machine）、极限梯度提升XGBoost（eXtreme Gradient Boosting）、随机森林RF（Random Forest）这类预测性能较好的决策树算法。同时考虑到多元负荷的时序特点，引入BiGRU，在第一层选取不同类型的基学习器，目的是使模型能从不同的空间结构去训练数据，从而达到更高的预测精度；在第二层元学习器模型选取LightGBM模型，以增强模型的泛化能力。

2）第二阶段：扩充原始输入变量。

对原始输入变量进行扩充，将第一阶段单独预测得到的电、热、冷负荷结果扩充至原始输入空间，组成新的输入变量，并且在传统Stacking 集成学习模型基础之上再引入一层多目标回归模型。为了防止出现过拟合现象，本文选取RGF 算法作为最终多元负荷协同预测模型，并同时输出电、热、冷负荷预测结果。

3 预测流程

本文提出的基于MIC 和多目标Stacking 集成学习的多元负荷预测方法的具体预测流程图如图3所示。

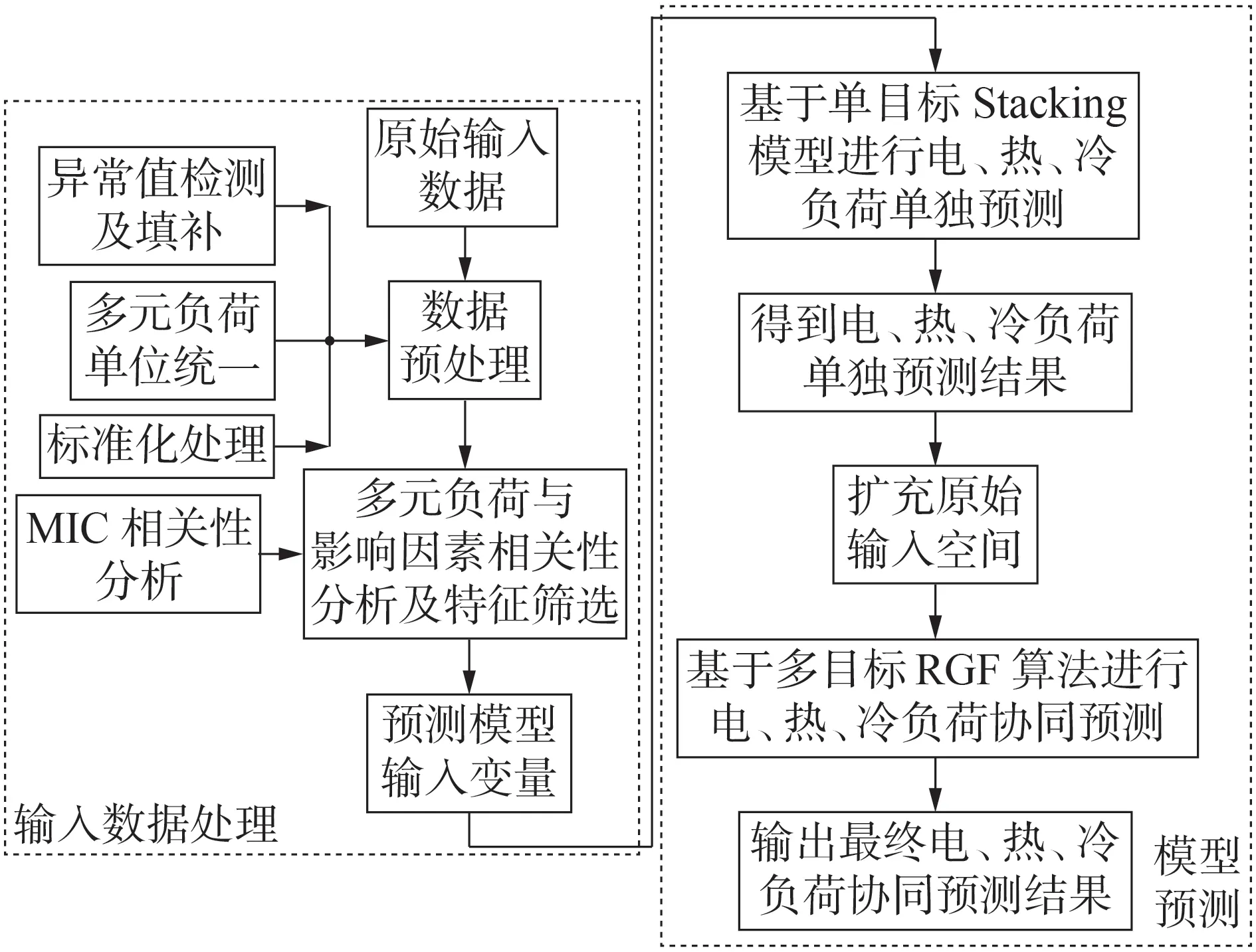
图3 所提预测方法流程图Fig.3 Flowchart of proposed forecasting method

4 算例分析

本文采用的实际数据为美国亚利桑那州立大学Tempe 校 区2019 年1 月1 日 至2020 年2 月29 日 的IES电、热、冷负荷数据，采样间隔为1 h，负荷数据来源于该校CAMPUS METABOLISM 项目网络数据库，天气数据来源于Dark SKY 网站。该校区拥有288 座建筑物、52 255 名师生，同时拥有冷热电联供CCHP（Combined Cooling，Heating and Power）、电锅炉、燃气锅炉以及电转气P2G（Power-to-Gas）等能量转换设备。

为了验证本文模型在一年不同季节下的适用性，根据气象学定义的四季，对美国亚利桑那州立大学Tempe 校区的IES 负荷数据进行四季划分，并以夏季和冬季为例，选取2019 年6 月1 日至8 月27 日的电、热、冷负荷数据及天气因素作为夏季预测的训练集样本，8月30日作为夏季典型工作日预测样本，8 月31 日作为夏季典型周末预测样本；选取2019 年12 月1 日至2020 年2 月22 日作为冬季预测训练集样本，2 月25 日作为冬季典型工作日预测样本，2 月24日作为冬季典型周末预测样本。

本文使用的硬件设施为Inter Core i5-9300H 处理器、NVDIA GTX1660Ti 6 G GDDR6独立显卡，软件平台为Python3.7.1和MATLAB R2020a。

4.1 输入变量与数据预处理

1）考虑到在实际负荷数据记录工程中，人工失误会导致某一时刻负荷数据出现异常情况，因此本文采用3σ准则［18］来进行异常值检测，将检测得到的异常值当作缺失值处理，并采用K-最近邻KNN（K-Nearest Neighbor）算法进行缺失值填补。

2）由于采集到的电、热、冷负荷数据单位不统一，为了不影响模型的鲁棒性，将采用不同单位的负荷进行标准化处理，先根据能源转换计算公式［19］全部将单位统一为kW，再与其他天气因素数据进行标准化处理，标准化计算公式如下：

式中：μ为原始数据样本均值；σ为原始数据样本的标准差。

3）考虑到多元负荷的时序特性，在进行多元负荷协同预测时，不仅要考虑预测日t-1时刻和预测日前一天t-1／t／t+1 时刻的实际温度、湿度等天气因素，还要考虑预测日前一天t-1／t／t+1时刻的电、热、冷负荷数据。因此，结合上文多元负荷及天气因素的相关性分析，本文选取的输入变量如附录A 表A2所示。

4.2 评价指标

本文使用平均绝对百分比误差EMAPE、平均精度MA和加权平均准确度WMA来评价预测结果，在WMA的权重分配中，考虑到电力负荷的主导地位，将电、热、冷负荷的权重值分别设为0.6、0.2、0.2，计算公式分别如下：

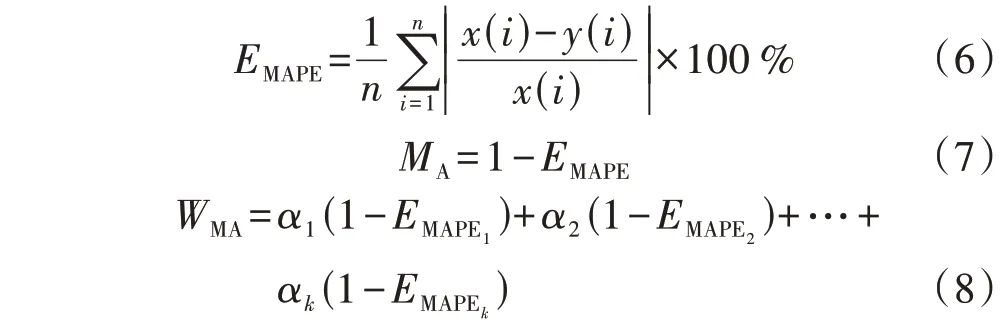
式中：n为样本数；x(i)为i时刻负荷实际值；y(i)为i时刻负荷预测值；αj(j=1，2，…，k)为第j类负荷的权重值；EMAPEj(j=1，2，…，k)为第j类负荷的平均绝对百分比误差值；k为负荷类型的数量。EMAPE值在0～100%之间，EMAPE值越小，预测误差越低；MA和WMA值在0～100%之间，MA和WMA值越大，预测精度越高。

4.3 参数选取

本文采用贝叶斯优化算法［20］对各模型进行参数寻优，各模型参数选取如表3所示。

表3 参数选取Table 3 Selection of parameters

4.4 预测结果对比分析

4.4.1 考虑负荷耦合形态指标前后的对比分析

为了验证本文所提出的负荷耦合形态指标能够提升模型的可预测性，设置以下2 种案例进行对比分析：案例1 考虑负荷耦合形态指标，采用本文模型进行电、热、冷负荷协同预测；案例2 不考虑负荷耦合形态指标，采用本文模型进行电、热、冷负荷协同预测。夏季和冬季考虑负荷耦合形态指标前后的电、热、冷负荷预测精度分别如表4和表5所示。

表4 夏季考虑负荷耦合形态指标前后的预测精度结果Table 4 Forecasting accuracy results before and after considering load coupling morphological indexes in summer

表5 冬季考虑负荷耦合形态指标前后的预测精度结果Table 5 Forecasting accuracy results before and after considering load coupling morphological indexes in winter

从表4 和表5 中可知，案例1 的预测精度优于案例2。在夏季典型工作日场景下，案例1的电、热、冷负荷预测误差EMAPE相较于案例2 分别减少了1.94%、1.22%、2.80%，预测精度WMA提升了1.97%；在冬季典型工作日场景下，案例1 的电、热、冷负荷预测误差EMAPE相较于案例2 分别减少了2.51%、3.73%、5.37%，预测精度WMA提升了3.33%。这表明本文所提出的负荷耦合形态指标增强了模型的可预测性。

4.4.2 多元负荷协同预测与单一负荷预测对比分析

为了验证多元负荷协同预测在不同时间步长下的普适性和优越性，将预测步长分别取1、6、12 h，并与单一负荷预测进行详细对比分析，以夏季为例，对比结果如表6 所示。从表中可知，随着预测步长的增大，多元负荷协同预测和单一负荷预测的预测误差EMAPE都逐渐变大，但在不同预测步长下，多元负荷协同预测模型都始终优于单一负荷预测模型。在典型工作日场景下，当预测步长为12 h时，多元负荷预测误差区间为［1.73%，3.74%］，而单一负荷预测误差区间为［5.33%，7.24%］，误差明显增大。这是因为多元负荷间具有较强的耦合关系，而单一负荷预测忽略了多元负荷间的耦合关系。

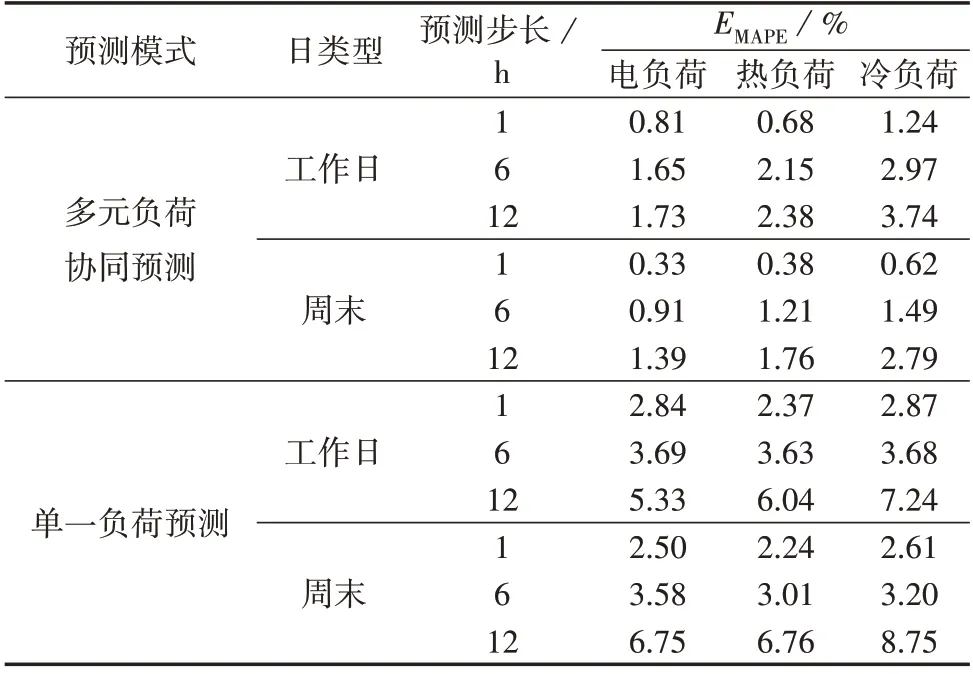
表6 不同预测步长下的多元负荷协同预测与单一负荷预测精度对比结果Table 6 Comparison results of forecasting accuracy between multivariate load collaborative forecasting and single-load forecasting in summer with different forecasting step sizes

在同一预测步长下多元负荷协同预测所花费的时间为35.38 s，而各负荷单独预测所花费的时间分别为电负荷32.92 s、热负荷33.03 s、冷负荷32.00 s，多元负荷协同预测的训练时间仅为单一负荷预测训练时间总和的1/3 左右。以上分析充分验证了多元负荷协同预测模型的优越性。

4.4.3 多模型融合与单一模型对比分析

为了验证本文采用的多模型融合的协同预测模型在预测精度方面的优势，将本文模型与集成学习中各单一模型算法进行对比，进行对比的单一模型算法包括RGF、XGBoost、BiGRU算法，为了保证实验的公平性，仍采用相同数据进行分析，并以夏季为例，具体实验结果如附录A图A3、A4和表7所示。

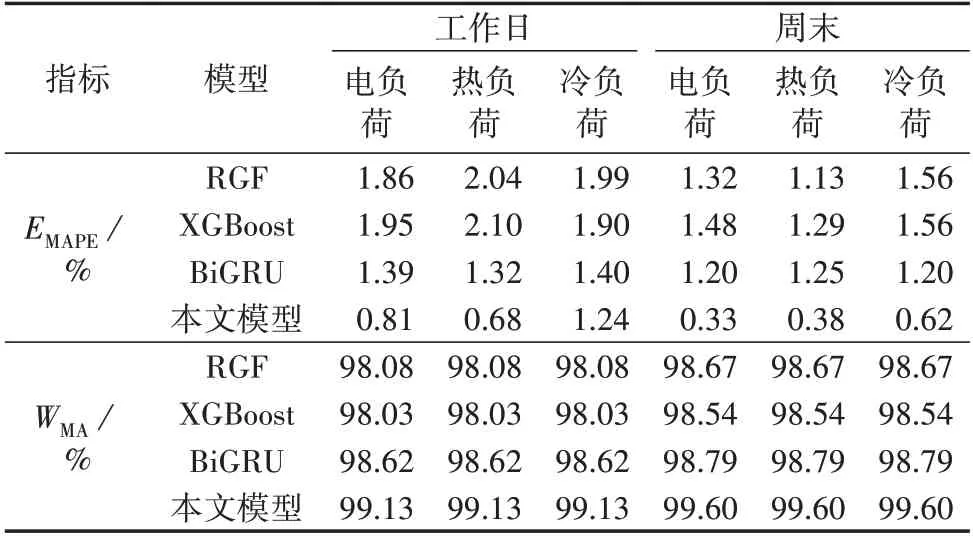
表7 多模型融合与单一模型预测对比结果Table 7 Comparison of forecasting results between multi-model fusion and single model

从表7 中可知，在不同日类型场景下，本文所提出的多模型融合的协同预测模型在预测精度WMA上均优于各单一预测模型。在典型工作日场景下，本文模型的电、热、冷负荷的预测误差EMAPE分别为0.81%、0.68%、1.24%，而基于XGBoost 的模型预测结果最差，EMAPE分别达到了1.95%、2.10%、1.90%，分别为本文模型预测误差的2.41 倍、3.09 倍、1.53倍；在典型周末场景下，本文模型的电、热、冷负荷的预测误差EMAPE分别为0.33%、0.38%、0.62%，而基于XGBoost的模型预测结果仍为最差，EMAPE分别达到了1.48%、1.29%、1.56%，分别为本文模型预测误差的4.48 倍、3.39 倍、2.52 倍。通过与各单一预测模型进行对比，再次验证了多模型融合的协同预测的优越性。

4.4.4 不同多元负荷预测模型对比分析

为了进一步突出本文所提出的多元负荷协同预测模型的优势，选取多目标回归和多任务学习算法来进行对比分析。其中多目标回归选取的学习器为LightGBM 算法，多任务学习算法的共享层选取BP神经网络来进行共享学习，以冬季为例，对比实验结果如图4、5和表8所示。

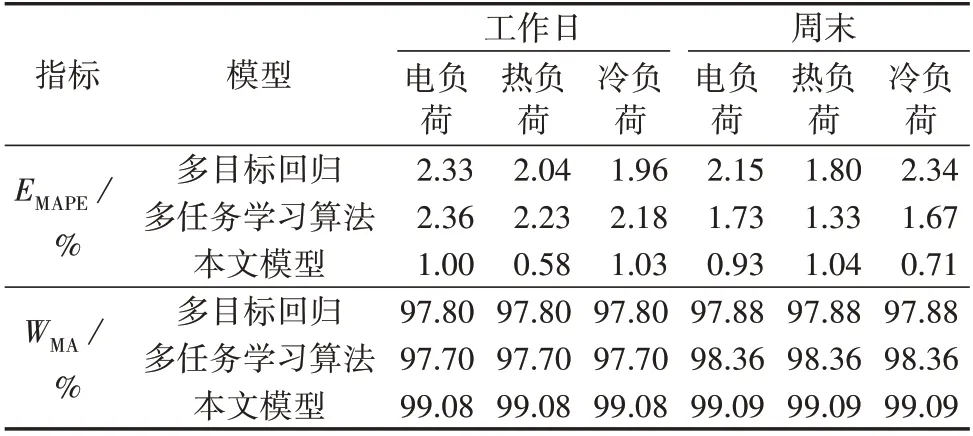
表8 不同多元负荷预测模型的预测结果Table 8 Forecasting results of different multivariate load forecasting models

从图4 和图5 中可知，在冬季典型工作日场景下，电、热、冷负荷预测相对误差最大值主要集中在工作时段，即08:00—19:00时段；在冬季典型周末场景下，电、热、冷负荷预测相对误差最大值主要出现在00:00—05:00、20:00—24:00 时段。本文所提出的多元负荷协同预测模型总体误差波动较为平稳，而其他2 种多元负荷预测模型误差波动则较为剧烈，主要有以下3点原因。

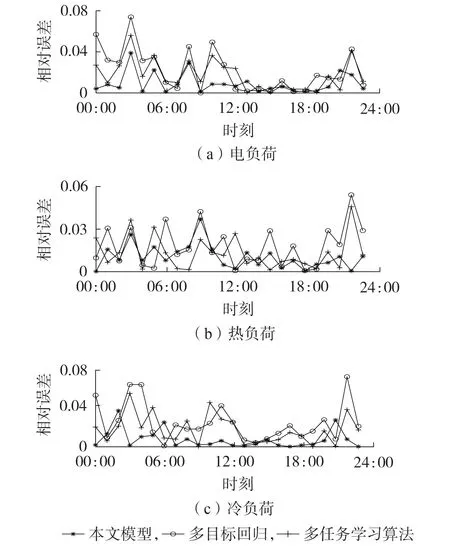
图5 冬季典型周末多元负荷预测模型相对误差对比图Fig.5 Relative error comparison diagram of multivariate load forecasting model on typical weekends in winter

1）本文采用的多模型融合下的多元负荷协同预测模型，通过选取不同类型的算法来达到互补的作用，其中树模型算法可以很好地学习多元负荷及天气因素之间的非线性关系；BiGRU 可以从不同方向全面地对数据进行学习；RGF 算法可以在单一负荷误差波动较为剧烈时，能从不同数据结构空间去学习多元负荷间的耦合信息，防止发生过拟合现象。

2）多目标LightGBM 算法不具有处理时间序列的功能，因此在处理时序特点较为明显的数据时具有明显的劣势。

3）多任务学习算法虽然在共享层学习了多元负荷间的耦合关系，但BP 神经网络的网络层较为简单，无法更深层次地挖掘多元负荷间的耦合信息。

从表8 中可知，在预测精度方面，本文采用的协同预测模型的预测误差EMAPE在［0.5%，1.1%］区间之内，而其他2 种多元负荷预测模型预测误差EMAPE在［1.3%，2.4%］范围内，可见本文模型明显优于其他2种模型。对于预测精度WMA值，本文模型也优于其他2种模型。

综上所述，本文所采用的多元负荷协同预测模型，在Stacking 集成学习框架下进行多模型融合，同时引入BiGRU 神经网络和RGF 算法作为学习器模型，前者可以从不同方向对数据进行全面的学习，后者能防止过拟合现象的发生。为了充分利用多元负荷间的耦合关系，将多目标回归思想与多模型融合相结合来实现多元负荷协同预测。

5 结论

本文考虑IES 中电、热、冷负荷之间的耦合关系，提出负荷耦合形态指标来深度挖掘多元负荷间的耦合性，并引入MIC 的相关性分析来进行特征筛选，再将多目标回归与Stacking 集成学习相结合，建立电、热、冷负荷协同预测模型，最后通过实际算例得出以下结论：

1）在考虑负荷耦合形态指标的情况下，协同预测模型较好地利用了多元负荷间的耦合信息，本文模型的预测精度得到了明显提升；

2）本文模型解决了传统Stacking 集成学习模型只能进行单一目标预测的问题，并在不同预测步长下证明了多元负荷协同预测相较于单一负荷预测受到预测步长的影响较小，预测精度和训练时间明显优于单一负荷预测；

3）在Stacking 集成学习模型中，分别引入RGF算法和BiGRU，前者能够防止过拟合现象的发生，后者能够从不同的数据方向学习信息，并且与其他多输出预测模型相比，其具有更高的预测精度且相对误差曲线波动较为平稳，模型的稳定性更强。

在之后的研究中，笔者将进一步考虑多元负荷时序耦合特性，挖掘更深层次的耦合特征，从而进一步提升预测精度。

附录见本刊网络版（http：//www.epae.cn）。