树形双边贯通供电方案及其应用研究

晏 寒，解绍锋，王 辉，刘 炜，张继雄，冯文杰

（1. 西南交通大学 电气工程学院，四川 成都 611756；2. 神华新朔铁路有限责任公司，内蒙古 鄂尔多斯 010300）

0 引言

我国现行电气化铁路为减小三相电压不平衡对电力系统的影响，多采用循环换相的异相供电方式［1］，该方式在牵引变电所和分区所处存在电分相。电分相是牵引网上的薄弱环节，会造成列车速度和牵引力的损失［2-3］，对于长大坡道，情况尤为严重，若列车无法靠惯性驶出无电区，将造成“坡停”事故。在重载、长大坡道线路或铁路枢纽站所，列车再生制动能量可达牵引能量的10%～30%，然而由于电分相的存在，相邻供电臂无法实现功率交换，导致线路列车的再生制动能量难以被直接利用，造成能量浪费［4］。长期以来，为解决电分相问题，多种自动过分相方案被提出［5］，这些方案虽然提高了列车通过电分相的自动化程度，但在过分相期间仍然存在断电过程。这一过程往往伴随着过电压、过电流、弓网电弧等暂态过程［6］，严重时会导致牵引网或列车故障，影响高速、重载列车的安全可靠运行。

我国电气化铁路正向着高速化、重载化的趋势发展，这对牵引供电系统的供电能力提出了新的挑战。电气化铁路双边供电可作为解决上述挑战的技术手段之一，其不仅可以提高牵引网电压，减小牵引网损耗，提升牵引网供电能力，还能够取消分区所处的电分相，提高系统的供电可靠性和再生制动能量利用率。目前，双边供电在俄罗斯等国家有广泛应用，其方式视为一种平行双边供电，存在均衡电流问题，会造成额外的电费计量，增加电气化铁路运营成本。随着组合式同相供电技术越来越多地被成功应用，可以在消除一半电分相的同时治理电能质量问题［7-10］。为了进一步提高供电能力，解决当前牵引供电系统中存在的不足，将组合式同相供电和双边供电结合的全线无分相贯通供电受到越来越多的关注［4，11］。文献［12］提出了一种树形双边供电方案，在满足参与双边供电的两牵引变压器变比相等的情况下，不存在均衡电流。针对树形双边供电，文献［13］介绍了其供电方案，但仅对单线牵引网模型进行了分析。目前国内电气化铁路多为复线牵引网，其等效模型更加复杂，需进一步建立模型分析。

本文对树形双边贯通供电方案进行了研究，以复线直接供电方式为例，建立了复线双边贯通供电的牵引网模型，分析其在不同并联方式下的牵引网等值阻抗；构建了树形双边贯通供电系统的通用链式电路模型，给出了潮流计算方法；将树形双边贯通供电方案应用于某重载铁路贯通供电改造，通过仿真分析对比既有供电方案与贯通供电方案的供电能力和能耗情况。

1 树形双边贯通供电方案

树形双边贯通供电方案外部电源如图1 所示，牵引供电方案如附录A 图A1 所示。正常供电时，2个牵引变电所SS1和SS2的外部电源来自同一电网的220 kV 或110 kV 电力变电站同一母线的不同分段，由于牵引供电系统为一级负荷，需由2 个独立的外部电源S1和S2供电（图中S1投运，S2作为备用）。在牵引变电所SS1和SS2分别设置由单相牵引变压器TT 和同相补偿装置CPD 组成的单相组合式同相供电装置［11］，每个所内设2 套装置互为备用，在取消牵引变电所出口处电分相的同时治理了电能质量问题；分区所SP 连通，形成树形双边供电，取消分区所处电分相，实现无分相贯通供电。图A1 中：牵引网为直接供电方式；T1和T2分别为上、下行接触网；R1和R2分别为上、下行钢轨。

图1 树形双边贯通供电方案的外部电源示意图Fig.1 Schematic diagram of external power supply source of tree bilateral continuous power supply scheme

2 树形双边贯通供电系统牵引网等值阻抗

单线牵引网不存在上下行电磁耦合，其结构和分析方法较为简单。复线牵引网由于上下行的电磁耦合，电气特性更加复杂，分析方法也与单线牵引网有所不同。复线牵引网通常进行上下行末端并联或全并联，为对比分析，下面将以直接供电方式为例，对双边供电区间上下行不并联、末端并联和全并联3种形式的牵引网阻抗进行分析［14-15］。另外，考虑当列车驶出双边供电区间后，类似于传统的单边供电，仅从端头牵引变电所的一侧供电臂取电，也对该情形的单边供电模型进行分析。

2.1 双边供电区间不并联直供牵引网

双边供电区间不并联直供牵引网归算到牵引侧的等值电路如图2所示。图中：E为电力系统归算到牵引网侧的电动势；I1和I2分别为左侧和右侧牵引变电所馈线电流；U1和U2分别为左侧和右侧牵引变电所处上行接触网对钢轨的电压；U＇1和U＇2分别为左侧和右侧牵引变电所处下行接触网对钢轨的电压；A为列车所在位置到其左侧牵引变电所的距离；L为构成双边供电的两牵引变电所之间的距离；IT11和IT12分别为列车处左、右两侧接触网电流；IR11和IR12分别为列车处左、右两侧钢轨电流；IT2为下行接触网电流；IR2为下行钢轨电流；I为列车取流；ZT1和ZT2分别为T1和T2的自阻抗；ZR1和ZR2分别为R1和R2的自阻抗；ZT1R1和ZT2R2分别为T1和R1之间、T2和R2之间的互阻抗；ZT1T2为T1和T2之间的互阻抗；ZR1R2为R1和R2之间的互阻抗；ZT1R2和ZT2R1分别为T1和R2之间、T2和R1之间的互阻抗；ZS1和ZS2为两牵引变电所折算到牵引网侧的电力系统阻抗，其值见式（1）。

图2 双边供电不并联直供牵引网等值电路Fig.2 Equivalent circuit of bilateral no-parallel direct power supply network

对图2 所示的等值电路进一步简化，并且进行Y／△变换，可得到图3 所示的简化电路。从图3 中电流I处看进去的不并联牵引网等值阻抗ZP1为：

图3 双边供电不并联直供牵引网简化电路Fig.3 Simplified circuit of bilateral no-parallel direct power supply network

2.2 双边供电区间末端并联直供牵引网

双边供电区间末端并联直供牵引网归算到牵引侧的等值电路如附录A 图A2（a）所示，在分区所处设置并联线。将图A2（a）进一步简化并经Y／△变换可得如图A2（b）所示的简化电路。从图A2（b）中电流I处看进去的末端并联牵引网等值阻抗ZP2为：

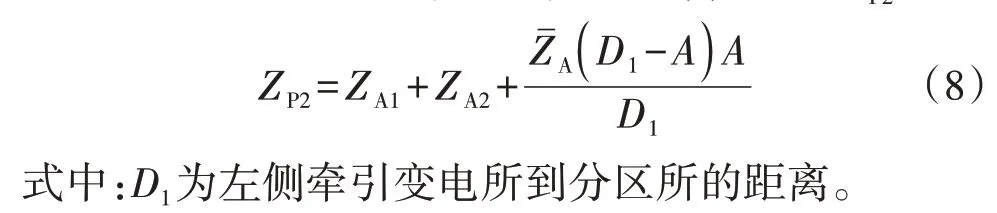
2.3 双边供电区间全并联直供牵引网

双边供电区间全并联直供牵引网归算到牵引侧的等值电路如附录A 图A3（a）所示，在区间内每隔一定距离设置一次并联线。将图A3（a）进一步简化并经Y／△变换可以得到如图A3（b）所示的简化电路。从图A3（b）中电流I处看进去的全并联牵引网等值阻抗ZP3为：

式中：D2为列车所在并联区段的长度；x为列车到其左侧并联线的距离。

2.4 单边供电直供牵引网

列车驶出两牵引变电所之间的双边供电区间后，仅从一侧供电臂取电，即单边供电。该情形的模型与双边供电模型类似，但2 个电源都在列车的同一侧，可沿用前述戴维南等效电路的方法分别对端头供电臂末端并联及全并联方式进行分析。

2.4.1 末端并联

端头供电臂末端并联，其归算到牵引侧的等值电路如附录A 图A4（a）所示。将图A4（a）进一步简化，得到的简化电路如图A4（b）所示。从图A4（b）

3 树形双边贯通供电系统链式电路建模及潮流计算

为使模型能够在双边供电与单边供电之间、末端并联与不并联之间灵活可调，将以牵引变电所为单元构建全线的链式电路模型［16］，相邻牵引变电所之间以分区所π 型等值电路连接，进而将整条线路描述在一个矩阵中，形成全线的节点导纳矩阵和电流矩阵［17］。

全线链式电路模型如图4 所示。图中：Zsp为纵向连接阻抗矩阵；Ysp为横向连接导纳矩阵；设牵引变电所左、右供电臂切面数量分别为hk和wk（k=1，2），IL1（i）（i=1，2，…，hk）和IR1（j）（j=1，2，…，wk）分别为SS1左、右供电臂切面处的电流矩阵；ZL1（i）和ZR1（j）分别为SS1左、右供电臂相邻切面之间的阻抗矩阵；YL1（i）和YR1（j）分别为SS1左、右供电臂切面的对地导纳矩阵；Iss1为SS1牵引变压器电流矩阵，其所在切面为牵引变压器切面；Zss1为牵引变压器切面到右侧供电臂第一个切面之间的阻抗矩阵；Yss1为牵引变压器切面对地导纳矩阵，Yss1除含有原对地导纳矩阵外，还有一附加矩阵YS1，用于反映系统侧阻抗对牵引网模型的影响。

图4 全线链式电路模型Fig.4 Chain circuit model of all line

以复线直供牵引网为例，导线排列顺序为上行接触网、上行钢轨、下行接触网和下行钢轨，则YS1为：

式中：δ为很小的实数（如10-6），表示牵引网导线之间存在纵向连接；Δ为很大的实数（如106），表示导线之间存在横向连接。

将Zsp中上下行接触网对应的自阻抗设置为Δ，即可将双边供电模型转换为单边供电模型。将Ysp中接触网和钢轨之间的自导纳和互导纳分别设置为δ和-δ，即可将末端并联模型转换为不并联模型。对于2.3 节及2.4.2 节所述的复线牵引网全并联模型，在图4 对应的存在横向并联线的切面中附加导纳矩阵Ysp即可。

第k（k=1，2）个牵引变电所单元的节点导纳矩阵Yk和电流矩阵Ik可分别表示为式（14）和式（15），进而，全线的节点导纳矩阵Yall和电流矩阵Iall可分别表示为式（16）和式（17）。

设Uall为全线的节点电压矩阵，则基于全线的节点电压方程为：

根据链式电路模型的特点，在负荷过程仿真中，每个时刻的牵引网潮流计算只需要形成1 次牵引供电系统节点导纳矩阵，然后根据设定的初始电压和电流进行迭代。具体迭代步骤如下。

步骤1：读取牵引计算数据，生成运行图文件，确定每个时刻t牵引网上所有列车的位置。

步骤2：获取仿真条件和线路参数，包括牵引变电所数量和位置、当前时刻线路列车的数量和位置、牵引网导线线型和数目。

步骤3：根据牵引网长度、牵引变电所和牵引负荷分布位置，划分牵引网切面，计算各切面之间的节点导纳矩阵。

步骤4：对各切面进行处理，根据式（14）和式（16），形成全线节点导纳矩阵Yall。

步骤5：根据初始电压计算牵引变电所和列车切面的电流向量，并根据式（15）和式（17）形成全线电流矩阵Iall。

步骤6：根据式（18）求解全线节点电压矩阵Uall，设各节点电压向量为Ui。

步骤7：将列车视为功率源，设Stri为第i辆列车的功率，Utri为所在切面的节点电压，则列车的修正电流为Itri=(Stri/Utri)*。

步骤8：重新形成新的全线电流矩阵I＇all，根据式（18）求解出新的全线节点电压矩阵U＇all，从而得到新的各节点电压向量U＇i。

步骤9：设收敛精度为ε，若满足||U＇i|-|Ui||≤ε则迭代收敛，转入下一步；否则用新的全线节点电压矩阵U＇all代替之前的Uall，转至步骤7，继续迭代，直至收敛。

步骤10：保存当前时刻各切面的支路电流和节点电压，仿真进入下一时刻，t＇=t+Δt，其中Δt为仿真时间步长。

步骤11：若仿真时刻达到了设定的仿真时长T，则保存这一时间段的负荷过程仿真结果，仿真结束；否则，转至步骤2。

4 应用研究

将树形双边贯通供电方案应用于某实际复线重载线路贯通供电改造。该重载线路全长约130 km，既有方案供电示意图如附录B 图B1（a）所示，全线设置4 个牵引变电所和3 个分区所，共7 处电分相，各供电臂均设置末端并联。采用树形双边贯通供电方案后，全线由同一相序供电，其示意图如附录B 图B1（b）所示，根据现行负荷情况，线路上设置两牵引变电所进行无分相贯通供电，原有SS0、SS3以及SP1—SP3改为开闭所。电力系统短路容量为1 000 MV·A，两牵引变电所均采用单相组合式同相供电方案，牵引变电所的外部电源来自同一个110 kV 电力变电站母线的不同分段，满足树形双边供电条件。

仿真参数中，设置接触线型号为CTAH-150，承力索型号为JTM-150，钢轨型号为P60。相关电气参数如附录B表B1所示［18］。列车车型为HXD4D，运行速度为80 km／h，功率因数为0.98，载重为10 300 t，牵引功率为14.4 MW。按发车时间间隔35 min 连续发车，运行图如附录B图B2所示。

4.1 阻抗模值对比分析

根据式（7）—（11），设全并联方式并联区段的长度D2分别为10 km 和5 km，绘制既有方案和贯通供电方案牵引网阻抗随距离变化的曲线如图5所示。

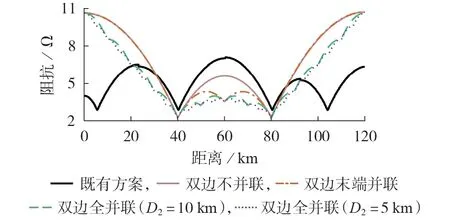
图5 牵引网等值阻抗曲线Fig.5 Equivalent impedance curves of traction network

由图5 可知，SS1和SS2的双边供电区间内，既有供电方案与双边供电不并联方案的牵引网阻抗最大值分别为7.14 Ω 和5.62 Ω，后者约为前者的79%。并且，双边供电牵引网上下行并联后，其阻抗最大值将进一步减小。

双边供电区间不同并联方式牵引网阻抗最大值之比随双边供电区间长度变化的曲线如图6 所示。由图可知，双边供电区间长度为40 km 时，末端并联、全并联（D2=10 km）和全并联（D2=5 km）牵引网阻抗最大值分别为不并联牵引网阻抗最大值的77%、71%和67%。并且随着双边供电区间长度的增长，该比例还将进一步减小。

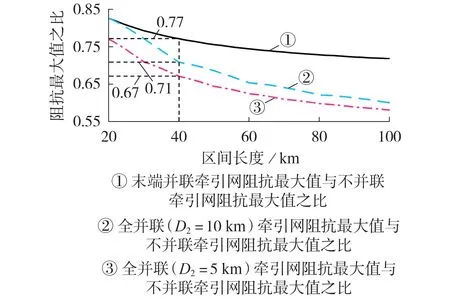
图6 双边供电牵引网阻抗最大值之比曲线Fig.6 Ratio curves of maximum impedance in bilateral power supply traction network

4.2 仿真结果对比分析

通过第3 节所述的仿真模型和潮流仿真算法对树形双边贯通供电方案进行仿真。仿真结果如图7和图8 所示，统计数据如表1 所示。图8 中，位置代表供电臂的具体里程。

图7 2种供电方案有功功率曲线Fig.7 Active power curves under two power supply schemes

图8 2种供电方式牵引网最低电压曲线Fig.8 Lowest voltage curves under two power supply schemes

表1 仿真结果统计对比Table 1 Statistical comparison of simulative results

由图8 可知：对于牵引网最低电压曲线，既有供电方案下为每个牵引变电所最低电压时刻该变电所供电范围内的电压曲线；树形双边贯通供电方案下为全线最低电压时刻的全线电压。

式中：n为牵引变电所数量，既有供电方案下n=4；树形双边贯通供电方案下n=2。

既有供电方案下，由于牵引供电臂之间存在电分相，列车再生制动产生的能量不能被其他供电臂处于牵引状态的列车利用，导致再生制动能量利用率较低。树形双边贯通供电方案下，全线牵引网无电分相，列车再生制动产生的能量能被牵引网其他供电臂上的列车利用，其再生制动能量利用率高，仿真结果显示，此方案下再生制动能量利用率为100%。

将2种供电方案对比后可知，树形双边贯通供电方案在减少牵引变电所数量的前提下，依然能满足供电能力的要求。设每个发车间隔（35 min）内，既有供电方案的再生制动能量利用量为SRU1，树形双边贯通供电方案的再生制动能量利用量为SRU2，则每个发车间隔通过再生制动可节省的电量ΔSRU为：

5 结论

在考虑复线牵引网上下行各导线电磁耦合的基础上，推导树形双边贯通供电牵引网数学模型，得到以下结论。

1）树形双边贯通供电牵引网上下行并联可以减小牵引网单位阻抗。减小并联区间长度可以进一步减小牵引网阻抗，减少电能损耗，延长供电距离。但并联过于密集将导致成本和维护难度增加，牵引网的可靠性也将受影响。因此实际工程应用时，并联间距应视发车间隔、线路条件等实际工况而定。

2）双边供电区间长度越长，并联与不并联牵引网单位阻抗之比越小，设置上下行并联对减小牵引网单位阻抗的效果越显著。这说明在长距离供电的情况下，适当对牵引网进行并联是有必要的。

3）以某实际重载铁路改造方案为例，对既有供电方案及树形双边贯通供电方案进行了仿真对比。结果显示，相较于既有方案，树形双边贯通供电方案的牵引网阻抗小，供电能力强，再生制动能量利用率达到100%，每年通过利用再生制动能量可节约电能约10.2 GW·h，节省电费约460.58 万元，具有良好的经济效益。

由于实例中进行贯通供电改造的重载铁路的牵引网供电方式为复线直接供电，本文主要对复线直接供电的树形双边贯通供电系统进行了研究，没有涉及其他的牵引网供电方案。在高速铁路中，自耦变压器供电方案被广泛应用，因此将树形双边贯通供电方案应用于高速铁路需要在以后的工作中进一步分析。

附录见本刊网络版（http：//www.epae.cn）。