竖向地震动峰值加速度作用下波纹板桥涵的变形特征
张永新
(六安市公路管理处,安徽 六安 237000)
0 引言
预制波纹钢结构与现浇混凝土结构相比具有诸多优点,如施工周期短、施工简单、使用寿命长、环保等。1992年,一条直径2.5m、总长3.2km预制波纹钢地下管廊在德国瓦豪工业园建成,被认为是最有代表性的波纹管地下管廊隧道之一。
部分学者已对波纹管施工展开了研究。例如,尹航等[1]采用有限元仿真方法对混凝土简支箱梁及波纹钢腹板PC 组合简支箱梁的力学性能进行了分析,研究表明混凝土结构的抗扭刚度能力强于组合简支箱梁结构; Kunecki 等[2]为验证波纹板结构的长期性能和巨大的承载能力,对1个跨度为2.99m、高度为2.40m 的波纹管涵洞进行了全尺寸静力试验;Yeau[3]介绍了俄亥俄州39 个在役波纹钢公路涵洞的现场性能测试结果,涵洞的跨度为3.23~7.04m,覆土高度为0.27~7.47m,通过驾驶重型卡车穿过涵洞进行静态和动态荷载测试;李祝龙等[4]通过现场试验对波纹管涵洞的力学性能进行了多方面研究,观察到波纹管涵洞顶部和两侧的应力和应变有不同的发展趋势,沿切线方向和轴线方向、波峰和波谷、内部和外部的应力和应变呈现相反的变化规律;针对重载铁路涵洞病害频发的现状,赵海军[5]提出了应用波纹板加固涵洞的方法,并对其加固效果进行了评估,研究发现波纹板加固对涵洞结构承载能力提高显著,能有效减少病害的发生。
预制波纹板结构的蓬勃发展促进了地震下动态特征研究的必要性,但目前相关研究较为缺乏。此外,国内目前还没有预制波纹钢结构的抗震设计相关规范。文献[6]~[9]对由波纹板建成桥梁结构进行研究,讨论了动力作用下波纹板桥梁结构的动力性能,但关于地下桥涵结构的动力响应研究还较为缺乏。
为此,本文将依托某实际工程,采用大型有限元软件ABAUQS 建立土层-结构作用的数值计算模型,探讨地震竖向分量对波纹板桥涵变形特征的影响规律,分析不同峰值加速度的地震竖向分量对钢波纹板桥涵结构变形的作用机制,为波纹板桥涵初步设计提供借鉴。
1 工程概况
某桥涵工程拟采用屈服强度为345MPa的波纹板(Q345钢材),波纹板波形尺寸为200mm×55mm×4mm(长×高×厚)。桥涵截面形式为管拱形,跨径5m,管顶填土高度4m。波纹钢桥涵结构如图1所示。本文选取典型断面作为研究对象,工程地址区的土体力学参数见表1。
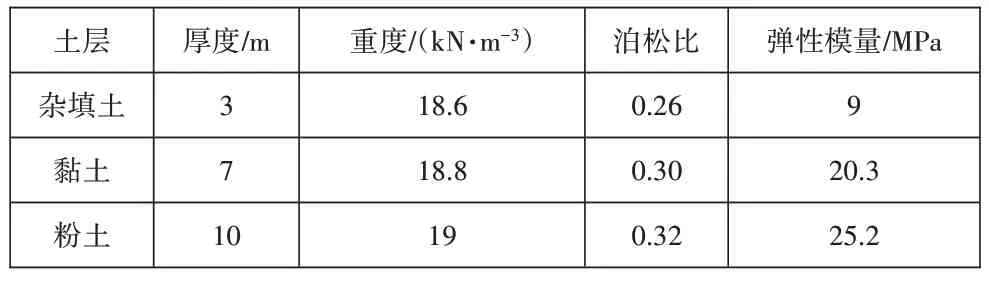
表1 土体物理力学参数

图1 波纹钢桥涵结构
2 有限元模型
为保证截取的人工边界能够满足地震响应需求,应使截断边界不影响波纹板结构的动力计算,截断边界一侧宽度应不小于结构宽度的3~5 倍,本文截取人工边界范围为35m×20m(长度×高度),所建有限元数值模型如图2所示。

图2 有限元模型
在截断人工边界处采用黏弹性人工边界,弹簧刚度及阻尼系数按式(1)~式(2)计算:
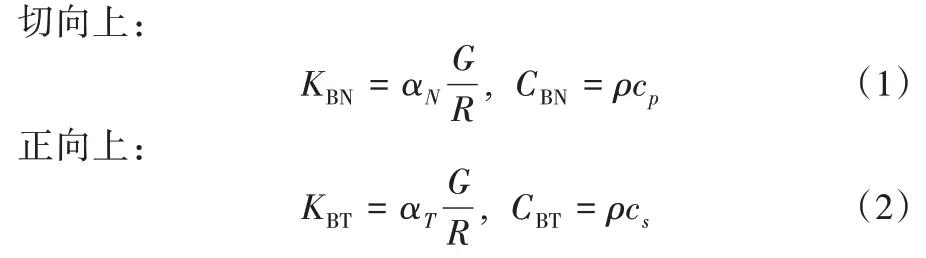
式(1)~式(2)中:KBN,KBT,CBN,CBT分别为人工边界法线方向和切线方向的弹簧刚度及阻尼系数;G为远场土体的剪切模量;ρ为远场地基的质量密度;R为波源到人工边界的距离。cp,cs分别为远场土体的压缩波和剪切波速度;参数αN,αT分别取1.33,0.67。
本文考虑地震作用下土体的非线性行为及循环特征,采用等效线性化的方法计算土体的非线性特征。通过EERA软件将地震波与土体的剪切波速作为初始条件,计算土体的等效剪切模量及阻尼比。在波纹板桥涵结构动力分析中,采用瑞利阻尼来模拟循环动荷载作用下土体的滞后性和非线性。黏性阻尼矩阵如式(3)所示:
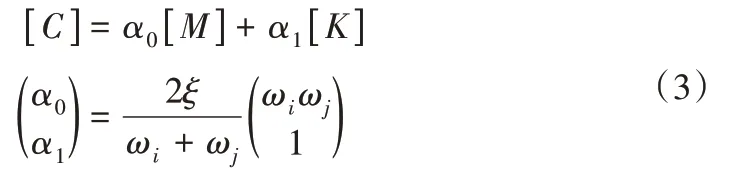
式(3)中:α0和α1为比例系数;ξ为阻尼比(本研究中为5%);ωi为土层的一阶固有频率;ωj是输入地震波主频;C,M,K分别为土体的阻尼矩阵、质量矩阵及刚度矩阵。
波纹板与周围土体相互作用特征采用基于ABAQUS 软件中的“罚函数”来模拟,分为法向和切向两个方向,其中法向采用硬接触,允许波纹板结构与土体发生分离;切向采用摩擦接触,摩擦系数取0.4。
3 地震波的输入
现以日本阪神地震的Kobe 地震波(如图3、图4 所示)数据为基础,对结构在地震作用下的力学响应进行分析。此次地震波的水平分量加速度最大值为0.3g,地震波的竖向分量加速度峰值范围为0.1g~0.7g。
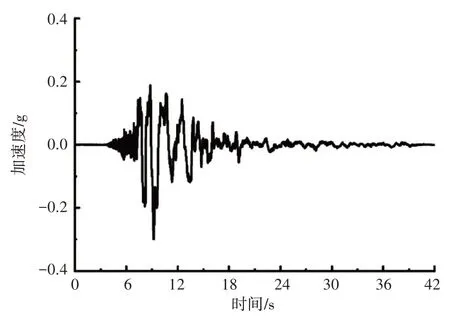
图3 Kobe地震波水平分量
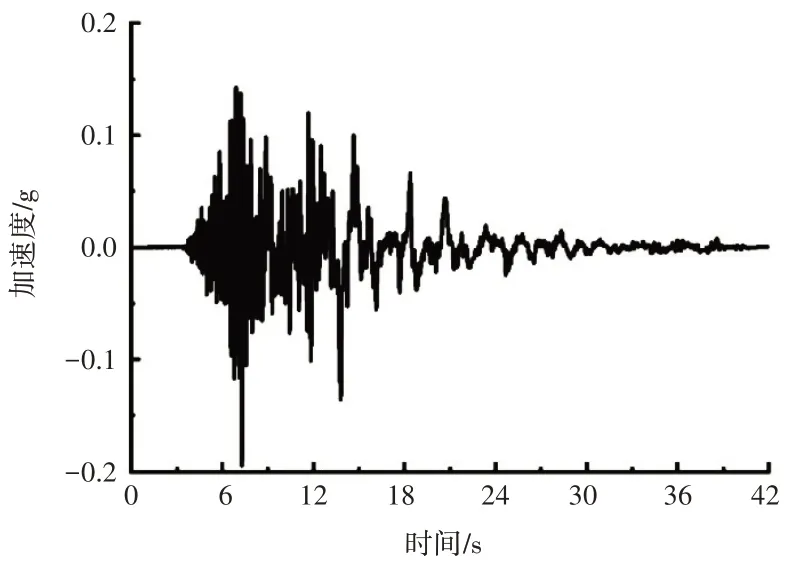
图4 Kobe地震波竖向分量
4 波纹板受力及变形特征分析
为更好地对计算结果进行分析,本文对波纹板结构角度进行划分,见图5。
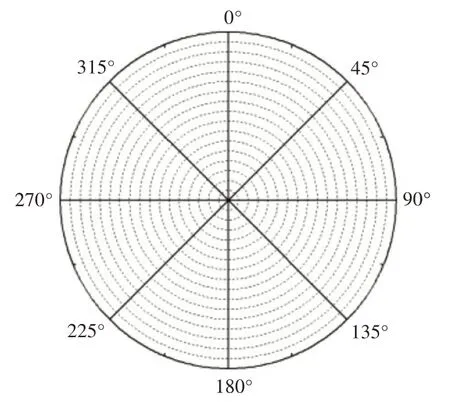
图5 波纹板角度标定
4.1 地震分量对波纹板结构力学响应特征影响分析
4.1.1 受力特征
不同地震分量作用下波纹板结构的应力云图如图6所示。

图6 地震作用下应力特征
由图6可知,地震竖向分量的存在使波纹板结构的最大Mises 应力减小了9.5%,但应力分布规律变化不大,最大应力均出现在124°左右。
4.1.2 变形特征
地震作用下波纹板结构变形特征如图7所示。
由图7结果可知,地震竖向分量的存在,使波纹板结构的变形模式发生巨大变化,由水平收敛变形转变成水平张开变形;在地震水平分量作用下,波纹板结构最大水平收敛变形为5.15mm,但在地震分量耦合作用下,波纹板结构的最大张开变形为23.45mm。
4.2 地震竖向分量对波纹板结构力学响应特征影响分析
4.2.1 受力特征
不同地震竖向分量峰值加速度作用下波纹板结构的应力分布如图8所示。可知,波纹板结构的应力分布特征受地震竖向分量峰值加速度的改变影响不显著,Mises 应力值在Amax=0.2g时出现转折点,最大Mises应力为2.9MPa。
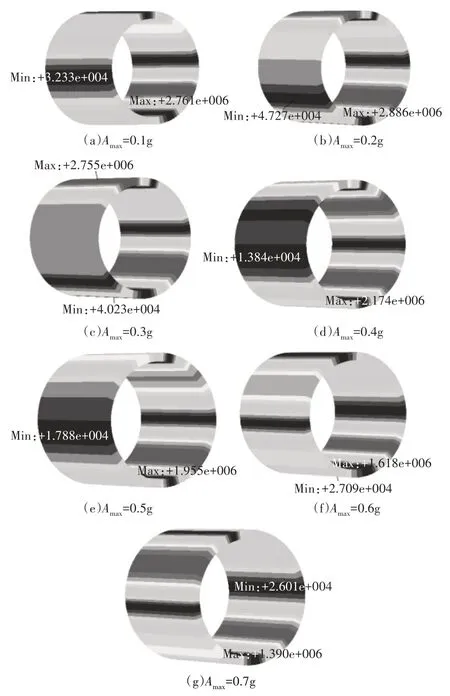
图8 波纹板结构应力特征
4.2.2 变形特征
不同峰值加速度地震竖向分量条件下,波纹板结构的水平、竖向变形规律如图9所示。可见,波纹板结构的水平张开量及竖向收敛量均随地震竖向分量峰值加速度的增大而增大,而竖向收敛变形值在Amax=0.3g 时出现最大变形值0.52mm。
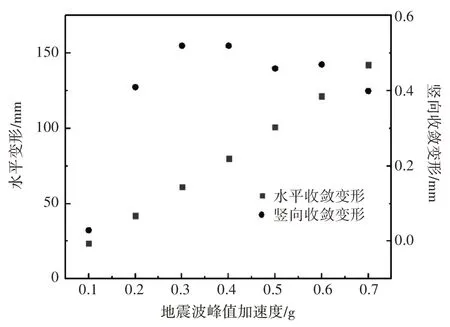
图9 不同地震竖向分量条件下变形特征
4.3 地震竖向分量强度与波纹板结构水平收敛变形的关系
基于上述分析获取了波纹板最大水平相对变形量与不同峰值加速度地震竖向分量的关系,通过回归拟合建立了两者的数据关系,如图10所示。
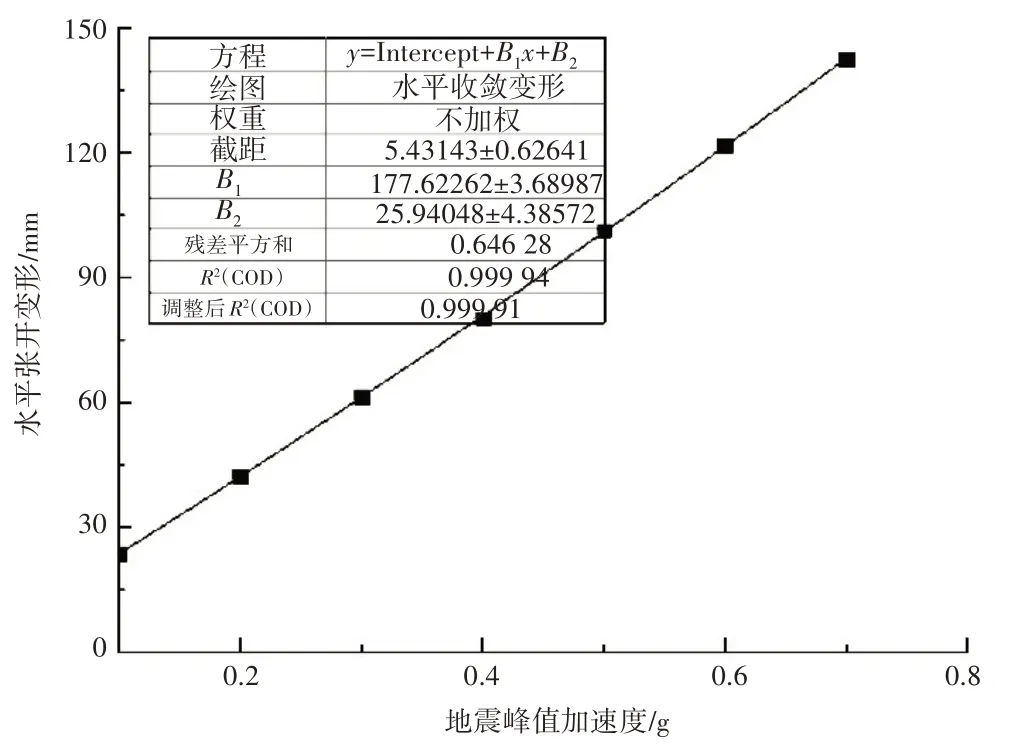
图10 波纹板结构水平收敛变形关系曲线
5 结论
本文依托大型有限元数值仿真软件,对土-波纹板结构之间的地震响应特征进行了研究,分析了钢波纹板桥涵结构的受力及变形受不同峰值加速度地震竖向分量的影响规律,进一步建立了波纹板结构水平变形量与地震竖向峰值加速度的关系式,所得结果如下:
(1)当地震竖向分量峰值加速度为0.1g 时,波纹板结构的最大Mises应力减小了9.5%,但应力分布规律受峰值加速影响较小,而波纹板应力分布基本不受地震竖向分量的影响;
(2)在地震水平分量作用下,波纹板结构水平收敛变形量可达5.15mm,而波纹板结构的变形模式受地震分量耦合作用影响显著,由水平收敛变形转变成水平张开变形,最大张开变形为23.45mm;
(3)随着地震竖向分量峰值加速度的增加,波纹板结构的竖向变形及应力在Amax=0.2g 时出现转折点,最大Mises应力为2.9MPa,但水平变形规律变化不大,且随着峰值加速度的增加而增大;
(4)本文建立的波纹板结构水平变形量与地震竖向峰值加速度的关系式可较直观地表征地震作用下结构的变形规律,可为波纹板桥涵设计提供借鉴。

