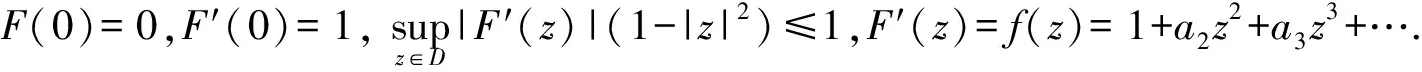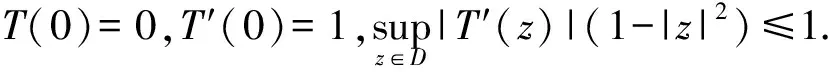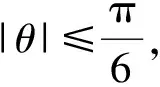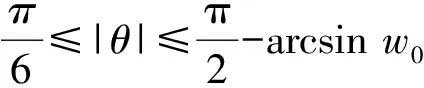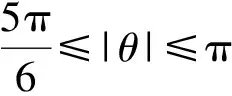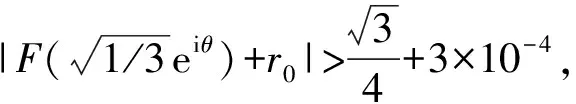Bloch常数的下界估计
王朝祥
(华侨大学 数学科学学院,福建 泉州 362021)
1 预备知识
单位圆盘D={z||z|<1}内的解析函数类记作H(D),对给定的F∈H(D),设BF表示F(D)包含的所有单叶圆盘的半径的上确界.Bloch常数B定义为B=inf{BF|F∈H(D),且F′(0)=1}.

2 主要结果
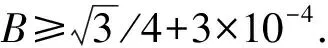
设F(z)∈B(D),且F′(0)=1,F′(z)=f(z)=1+a1z+a2z2+….由文献[8]可知a1=0,|a2|≤1,|a3|≤21/5.还需要用到如下的一些结论,即
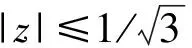
命题2[8]设F∈B(D),且F′(z)=f(z)=1+a2z2+a3z3+…,并假设ai∈R(i=2,3,…),则有

命题3[8]设F∈B(D),且F′(z)=f(z)=1+a2z2+a3z3+…,并设ai∈R(i=2,3,…),则当a3≥0时,有
2 引理及其证明
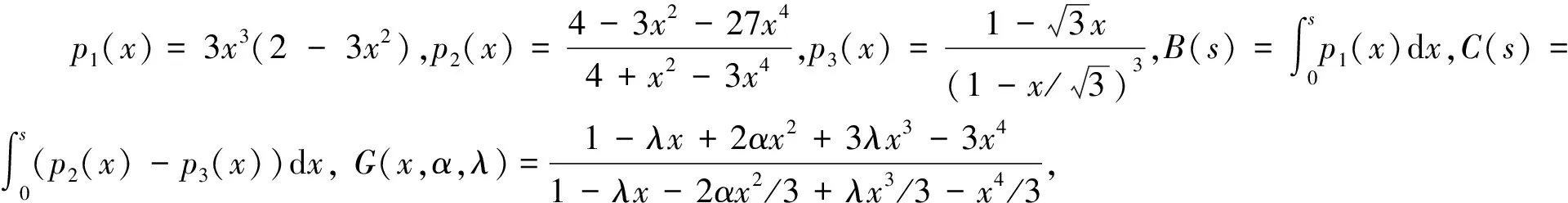
引理1设F(z)∈B(D),且F′(0)=1,F′(z)=f(z)=1+a1z+a2z2+…,则有
a1=0,|a2|≤1,|a3|≤21/5-|a2|2/2.
证明:Bonk[7]证明a1=0,|a2|≤1及|a3|≤5.Chen等[8]进一步证明了|a3|≤4.2.以下证明|a3|≤21/5-|a2|2/2.
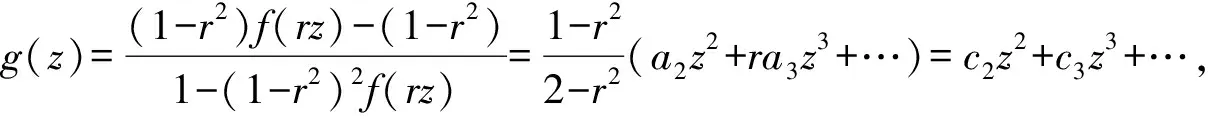
引理2设0≤x≤1,0≤θ≤1/5,令σ(θ,x)=(1-x)2(2arg(eiθ-x)-θ),则
(1)
式(1)中:k=407/625-(149ln 5)/5 625=0.608 5….
证明:只需证明0<θ≤1/5的情形.由于
所以有
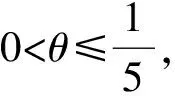
上式中:k=407/625-(149ln 5)/5 625=0.608 5….
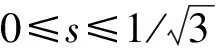
(2)

因此有
由命题2可知,当a3≤0,0≤t<1时,有
(3)
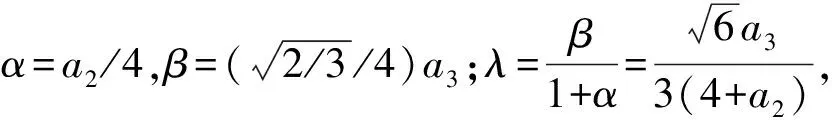
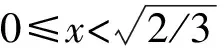

于是有
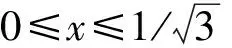
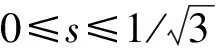
(4)
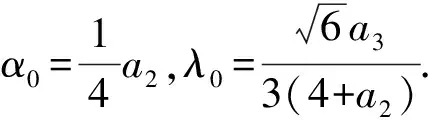
(5)
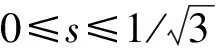
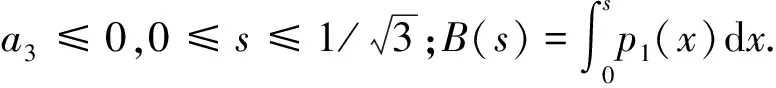
引理4设F∈B(D),且F′(z)=f(z)=1+a2z2+a3z3+…,并假设ai∈R(i=2,3,…),则有
(6)
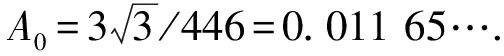
文[8]的引理2中估计式(6)得到的是A0=0.01 09,显然,文中的估计更优.

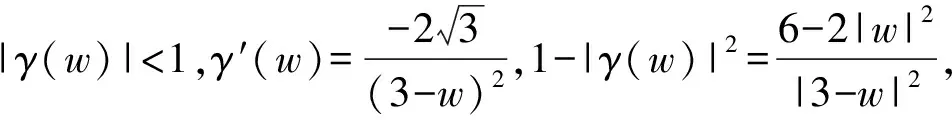
(7)
经积分可得
于是可得
(8)
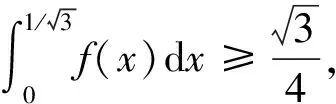
以下证明当-1 当|w|=r时,有 而由H(w)的定义可知其在|w|≤r上解析,因此,当|w|≤r时,|H(w)| 由此可得到 从而有 这说明当z=ρeiτ∈Γ且0≤ρ≤ρt时,总有Re(Φ(z))≥(1-t2)α成立. 因为对于∀z∈γt,总有0≤|z|≤ρt,且有Re(Φ(z))≥(1-t2)α,因此对于w∈ct总有Re(H(w))=Re(RΦ(z))≥R(1-t2)α. 上式中:k1=0.648 4…是找到的一个绝对常数.下面将对式(8)的积分进行估计. (9) 至此,引理4证毕. 引理5设F∈B(D),F′(z)=f(z)=1+a2z2+a3z3+…,并假设a3≥0,a2=|a2|eiθ0,|θ0|≤π/3.若0≤r<1,θ∈[-π,π],则有 上式中:|θ0|≤π/3;a3≥0;A2=|a2|cos(2θ+θ0),A3=a3cos 3θ,…,An=|an|cos(nθ+argan),…均为实数. 由Fθ(z)的定义可知 (10) 即可.在式(10)中,有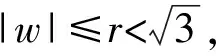
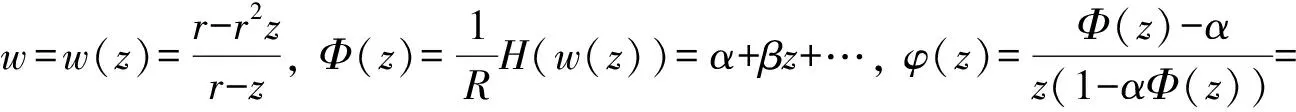
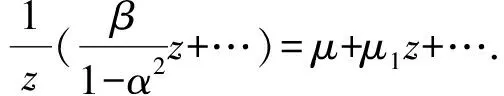
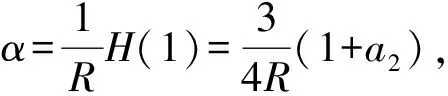
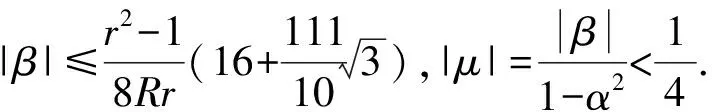

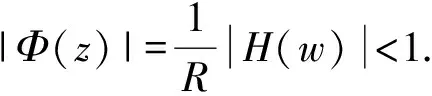
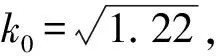
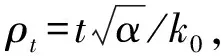
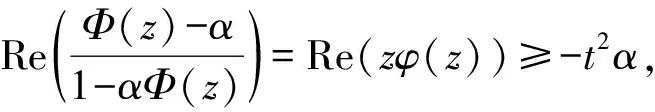
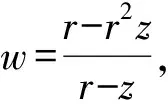
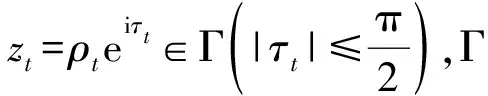


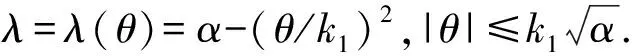
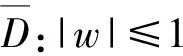
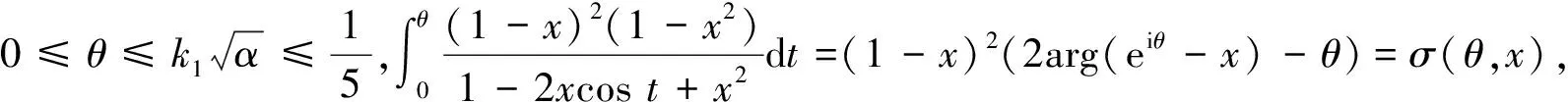
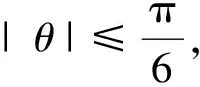
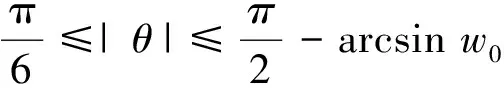
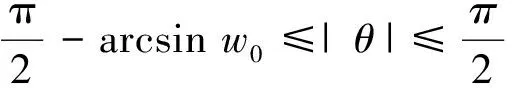
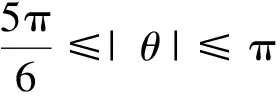
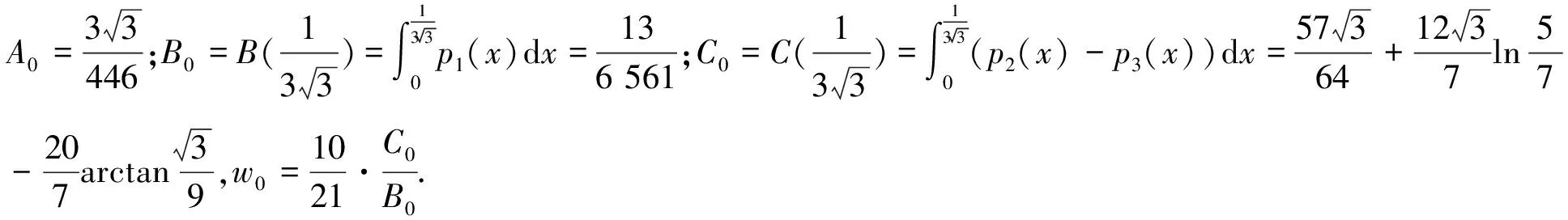
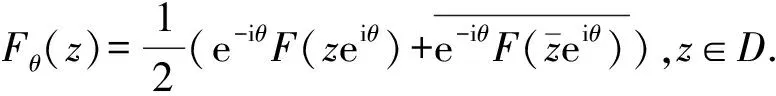
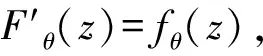


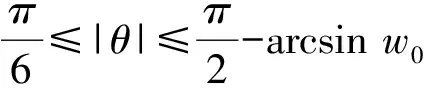

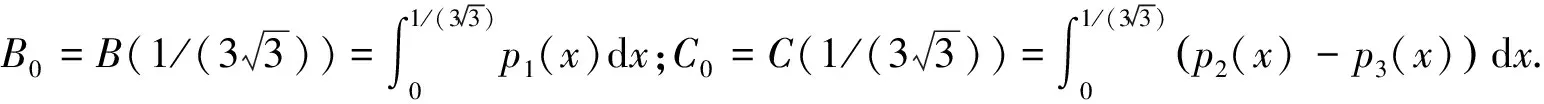
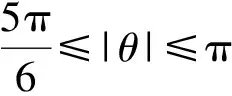
3 定理1的证明