轴心受压高强焊接圆钢管局部屈曲性能研究

郭伟涛,黄 斌,张文福,

(1. 安徽建筑大学土木工程学院, 安徽 合肥 230601；2. 南京工程学院建筑工程学院, 江苏 南京 211167)

高强焊接钢管由于具有良好的韧性、加工性和可焊性,被广泛应用于输电塔结构.在输电塔的设计中常采用三维桁架模型,其中杆件均为轴向受力.对于大直径钢管,在截面强度失效前出现局部屈曲现象不容忽视,这将导致材料利用率下降.为了避免钢管的局部屈曲采用一定径厚比(D/t)限值,而D/t超过限值的钢管,在不同规范中给出了不同的处理方法,DL/T 5154—2002[1]、ASCE/SEI 48—05[2]和AISC 360—10[3]采用考虑局部屈曲影响降低材料强度的方法；AS 4100—1998[4]采用等效直径的概念.对于高强度钢管,考虑到杆件的弹塑性局部屈曲和屈服强度有密切关系,应重新评估局部屈曲对其极限承载力的影响.近年来,一些学者对高强钢管短柱轴向受压的局部屈曲性能进行了研究.文献[5]进行了屈服强度为1 350 MPa(Q1350)的圆管短柱材料试验和局部屈曲试验；文献[6]研究了钢管的几何缺陷和残余应力,讨论了高强焊接圆钢管局部屈曲的长细比限值；文献[7]通过24根轴压柱试验研究了屈服强度为420 MPa(Q420)的高强焊接钢管柱的屈曲性能；文献[8]对42个样本进行轴向受压试验,得出现有的设计标准对于Q690钢管的设计都相对保守的结论；文献[9]对5根钢管和7根套管加固钢管进行了单调加载静力试验；文献[10]提出了槽口缺陷影响系数,并给出考虑槽口缺陷的圆钢管短柱极限承载力计算公式；文献[11]通过试验与有限元研究提出了高强圆钢管轴压构件整体稳定承载力的设计建议.通过这些文献可以发现,现有的关于高强度圆钢管轴向受压下局部屈曲研究主要集中在Q420、Q690、Q1 350的钢材试验上,但可以使用的精确数值分析并不多.本文在考虑初始几何缺陷和残余应力的情况下,采用有限元软件ANSYS建立轴压圆钢管的有限元模型,并对Q550、Q690、Q800、Q960轴压圆钢管的D/t限值和抗局部屈曲计算方法进行研究.

1 有限元模型

利用有限元软件ANSYS进行几何非线性和材料非线性分析,得到有限元计算结果.采用shell181单元对圆管进行离散,为了实现截面内外层残余应力分布的不同,将壳单元分为两层,沿着每层厚度方向设置一个积分点.初始残余应力在积分点处定义,初始状态条件用ISFILE命令写入ANSYS程序中的适当文件中.将圆管沿圆周方向离散为32个单元,每个单元均为方形,保证计算结果的收敛性和计算效率.构件一端固定,另一端约束沿截面方向的横向位移.使用ANSYS提供的CERIG命令形成刚周边,以确保构件端部均匀压缩.采用弧长法对构件的平衡路径进行跟踪,得到轴压作用下荷载与位移曲线的峰值.

1.1 初始缺陷

1.2 有限元模型的验证

在文献[8]中选取了24个用于研究Q690焊接圆管局部屈曲承载力的试件,有限元分析结果和现有试验数据的比较如图1所示,有限元的计算结果分别表示为N0.1、N0.03和N0.009,分别对应0.1E0、0.03E0和0.009E0.由图1可见：N0.03的结果与计算结果最相近,平均值(AVE)为1.01,标准差(SD)为0.02；N0.009的AVE和SD分别为0.93和0.46;在研究短柱的极限承载力时，Et是一个需要考虑的因素.本文使用与表1数据一致的0.009E0来扩展分析结果的通用性.

图1 有限元结果与试验结果的对比

2 有限元结果分析

2.1 有限元试件设计

目前,大多数设计规范都采用限制D/t或相关指标的方法来避免圆管的局部屈曲破坏,但具体的数值相差不大.根据文献[6]对屈服强度为1 350 MPa圆钢管的研究,表1根据D/t、λe=(D/t)(σy/250)和α=(E/σy)/(D/t)分类,总结了Q550、Q690、Q800和Q960钢的三种不同限值,其中AS4100的限值最严格, DL/T5154—2012的限值最为宽松.

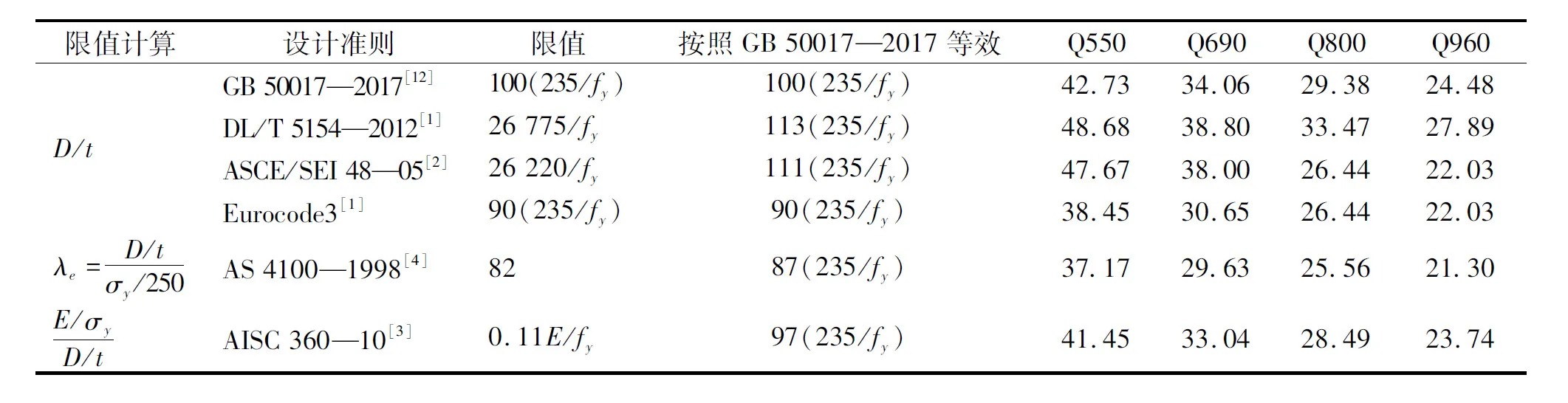
表1 圆钢管径厚比限值的估计值

对于Q690钢材,两者之间差异高达31%.本文基于有限元的计算结果,对局部屈曲的极限承载力重新进行评估.为了明确D/t限值,选用每个钢材型号30个试件,共120个有限元模型对试验数据进行扩展和补充,如表2所示.以CT89×4为例说明,其中CT表示圆管、89表示直径、4表示厚度.长度Le设为3.5D,以防止整体屈曲破坏,消除端部效应.

表2 有限元试件的参数

2.2 残余应力的影响

将三种不同的残余应力模式Shi[8,15]、Wagner[10,16]、Chen[11,16]分别引入有限元分析,分别计算每种钢材的3个截面(CT89×4、CT480×12和CT680×10).如图2所示, Wagner模式对极限承载力的影响最为显著,Chen模式对极限承载力的影响最小.总的来说,随着D/t的增大,残余应力效应变得更加突出;随着钢材等级的提高,同一截面的极限承载力折减程度增大,这与残余应力幅值与钢的屈服强度之比的减小正好相反.在之后的有限元分析中,数值计算主要集中在考虑残余应力Shi模式下进行.

(a) Q550

2.3 局部屈曲破坏全过程分析

以Q690圆管CT660×12为研究对象,探讨局部屈曲过程应力分布和变形的发展规律.CT660×12的荷载-轴向压缩位移曲线如图3所示,其呈现出典型的极值型破坏特征：当荷载达到最大值时,极限承载力迅速下降,变形过程中没有表现出明显的塑性.曲线上的5个监测点标记了柱体的变形模式,以监测破坏的形成过程.为了便于观察,放大图3的变形云图.在初始荷载(α=0.015)下,由于初始几何缺陷,构件的局部呈现菱形突起,除了两端截面设置刚周边外,其余截面在竖向压缩下沿径向膨胀,导致圆周拉伸；随着荷载进一步提高到α=0.575,截面的圆周不断扩大,构件的变形逐渐重新分布；当荷载达到极限承载力α=0.970时,由于偏心荷载和极限承载力的作用,在靠近两端的区域出现D/5左右的不对称局部屈曲,极限荷载急剧下降.参照监测点α=0.755,为了保持平衡,外力继续加载,短柱CT660×12受压时在端部出现明显的局部屈曲破坏,俗称象脚.根据监测点的变形形式,提出一个简化的力学模型(如图4所示)来解释象脚形成的力学机制：端部截面设置刚周边限制了端部的周向膨胀,而刚周边下方截面沿圆周向变形不受限制,考虑变形的连续性,构件表面形成一个斜平面,竖向压力沿着斜平面的水平方向的分力进一步促进了象脚的形成.因此,可以推断象脚形成的根本原因为：在竖向压力作用下,靠近端部的圆周膨胀程度不同且与初始缺陷无关(包括几何缺陷和残余应力),如图5所示.图5中,h≈5lelem=D/5，lelem为单元尺寸，D为钢管直径.图5中比较了命令NLGEOM打开或关闭情况下的变形情况,可见仍然可以观察到象脚现象.

2.4 D/t和局部屈曲极限的影响

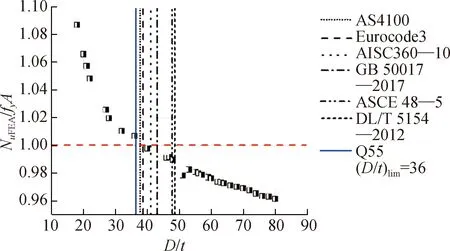
D/t用于定义截面分类并判断是否可以在局部屈曲之前实现全截面屈服.基于有限元结果建立圆钢管极限承载力和D/t的关系,如图6所示.当D/t超过一定极限时,圆钢管承载力小于整个截面的塑性承载力(fyA),而随着D/t的增大,承载力逐渐减小.将不同钢材等级的D/t限值标注在图6中,Q550的D/t限值为36,略小于AS 4100—1998给出的值；Q690的D/t限值为32,接近于AISC 360—10中给出的值； Q800、Q550的D/t限值分别为27和22,接近于欧洲规范3中给出的值.各国规范给出的径厚比限值如表1所示.

图3 荷载-轴向压缩位移曲线

图4 象脚现象的力学分析模型

图5 受压圆管的变形

3 设计指导

局部屈曲对构件承载力影响的计算方法可分为两类：1) 直接强度法(DSM),是将材料强度乘以折减系数,如DL/T 5154—2012、ASCE/SEI 48—05；2) 等效直径法,通过减小计算直径,如AS 4100—1998.

(a) Q550

3.1 直接强度法

为了弄清数量关系,然后估计局部屈曲对极限承载力的影响.根据有限元的计算结果,建立表示折减系数的公式为：

(1)

式中：mN为NuFEM/fyA的局部屈曲折减系数；fy为钢材的屈服强度；D为钢管直径；t为钢管厚度.

将有限元结果与DL/T 5154—2012、ASCE/SEI 48—05建议的公式进行比较,如图7所示,试验结果、有限元计算结果和规范设计计算结果有明显差距.以试验数据ZS-φ420×6[8]为例,试验数据的局部屈曲折减系数0.966比本文提出的公式大0.6%,比DL/T 5154—2012、ASCE/SEI 48—05分别大10.27%和10.62%.由于有限元分析中的变形模量Et明显低于试验数据的对应值,因此当fyD/t小于40 000(对于Q690,D/t=45)时,建议公式的结果和试验数据的差异大于11.8%,考虑到有限元模型中所用材料的本构关系具有良好的通用性,仍然可以认为该公式具有参考意义.

图7 强度折减系数mN和fyD/t

3.2 等效直径法

由于残余应力和几何初始缺陷的影响,部分截面的应力首先超过屈服强度而不能抵抗外荷载.对于圆钢管,截面的损坏通过等效直径De反映,在本文研究范围内建立计算公式：

(2)

试验数据、有限元计算结果和建议公式结果如图8所示.由图8可见,当λ>180时,试验结果与建议公式之差仅为0.2%,当λ<120(对于Q690,D/t=45)时,两者相差高达18%.当D/t非常小时,截面进入全截面屈服状态,两者之间的差距并不显著,式(2)用来计算圆钢管的极限承载力是可行的.

图8 有效直径De和λ计算结果

基于等效截面概念,在本文的研究范围内,圆管短柱的极限承载力计算公式为：

(3)

4 结论

本文在现有试验数据的基础上,对四种钢材等级的120个试件进行了有限元验证,阐明了残余应力、钢材等级的影响,同时对整个破坏过程进行了跟踪,探讨了圆管短柱局部屈曲的力学机理,并验证了现有计算方法对圆管短柱的适用性.研究结果表明：

1) 研究Chen、Shi、Wagner三种残余应力模式对极限承载力的影响,Wagner模式对极限承载力的影响最为显著,Shi的模式次之,Chen的模式对极限承载力的影响最小；

2) 通过对变形全过程的跟踪,发现象脚的形成主要是因为在轴向压力下靠近端部每个部分的圆周膨胀程度不同；

3) 为Q550、Q690、Q800、Q960圆管推荐了D/t限值,即为36、32、27、22,随着钢材等级的提高,应采用较小的D/t限值,以保证材料的利用率,对于相同截面,由于局部屈曲的影响,钢材等级越高,截面强度的降低越明显；

4) 考虑到DL/T 5151—2012、ASCE/SEI 48—05和AS 4100—1998中的公式计算结果过于保守,基于本文的研究范围提出了新的极限承载力计算公式.