基于梅尔频率倒谱系数的音频分类研究
屈晓渊,崔 青
(1.榆林学院 信息工程学院,陕西 榆林 719000;2.榆林学院 艺术学院,陕西 榆林 719000)
随着大数据技术的发展,越来越多的音频资源存储于网络平台之上,面对这些海量的资源,有效的资源检索技术显得尤为重要。如何在大量的音乐数据中快捷且准确地检索到所需的信息,对充分利用这些资源有着很重要的研究意义。
音乐的流派分类研究就是要求设计的分类系统能够根据所输入的音频,提取音频特征信息,从而识别出音乐的所属流派。这一研究对音乐信息检索(Music Information Retrieval,MIR)有着至关重要的作用[1]。在音频特征提取方面,根据不同的应用场景有诸多的提取方法,虽然在语音提取方面可以根据余弦相似度进行语音识别[2],或者基于PIFA 的语音识别[3]等方法,但是在音乐特征方面,这些算法的效果并不是特别理想。
文中从采样的音频数据提取出梅尔倒谱系数(MFCC)特征,并对MFCC 特征进行数据归一化处理。通过选择合适的神经元激活函数、损失函数计算方法,对优化器、训练精确度等参数进行设定,构建多层卷积神经网络模型,设计出一种音频数据分类模型。
1 音频特征提取
1.1 音频数据预处理
在音乐流派的分类过程中,可能存在着由于音乐数据来源不同而产生的音乐存储格式或采样频率不统一,且可能存在无用的干扰噪音等问题[4],因此需要对音频信号进行预处理操作。音频预处理的主要工作包括统一音频信号的存储格式、采样量化、加窗、分帧等操作,能够为音频分类研究中的特征提取步骤提供标准化、可靠的音频信号样本[5]。
1.1.1 音频信号的预处理
音频的数字化处理过程中有着两个重要的指标,分别为采样率与采样大小[6]。采样率定义为每秒钟从连续的音频信号中提取并组成离散的音频信号的采样个数,其单位为Hz。采样大小表示量化的过程,将该频率的能量值量化,用于表示信号强度。
文中采用22.05 kHz 的采样率对原始音频数据进行重采样,并将信号转换到单声道,同时设定合适的采样偏移量与持续时间。以蓝调、金属、流行风格音频为例,重采样后的波形图如图1 所示。

图1 重采样后音频波形图
对数据集中的歌曲样本进行分析,每个样本均为30 s 左右的播放时长,根据采样率进行重采样后,每一个歌曲样本均设定650 000 个采样点。
1.1.2 数据归一化处理
重采样后,需要对数据进行归一化处理,使训练集、测试集和验证集数据都具有相同的空间分布。针对音频特征,使用min-max 标准化方法进行处理,使结果分布于[-1,1]区间,公式如下:

其中,x为当前采样点,max 为样本数据的最大值,min 为样本数据的最小值。通过min-max方式标准化后,经测试可知,所有样本数据位于[-0.840 240 5,0.885 376]区间。
1.1.3 音频信号转换为单声道
音乐数据的规模是十分巨大的,且不能直接用于音乐检索系统。为了方便计算,需要对所有的音频数据统一格式,将多声道转化为单声道,统一用相同的采样率与采样大小进行采样等处理。
1.1.4 音频信号的预加重处理
为了增加语言的分辨率,去除环境对音频的干扰和影响,设定一定的滤波器对语音信号进行预加重处理。一般采用一阶FIR 高通数字滤波器来实现预加重处理,该滤波器的主要作用是加强高频信息、避免FFT操作中的数值问题、增加信噪比,见公式(2)。

其中,x(n)表示音频信号在某采样时刻的采样值,a∈[0.9,1],y(n)表示预加重处理后的结果。
1.2 梅尔频率倒谱系数特征提取
梅尔倒谱系数MFCC 是在Mel 标度频率域提取出来的倒谱参数,Mel 标度描述了人耳频率的非线性特性,即依据人的听觉实验结果来分析音频的频谱[7]。通过对音频信号进行的一系列数据转换得到便于分析的梅尔频率倒谱系数,其流程如图2 所示。

图2 梅尔频率倒谱系数提取流程
1)音频信号在宏观上和微观上显示出极大的差异,体现为宏观上的不平稳性和微观上的平稳性。在图1 音频波形图中可见音频信号宏观上的不平稳性,但是在每30 ms 左右音频显示出相对平稳的特点。在此情况下,将部分连续的n个采样点{xj,xj+1,…,xj+n-1}合并为一个帧Chunki,每个帧所涵盖的时间为Ti∈[20,30]ms。为避免相邻的帧之间数值差过大,设定合适的帧移k,用一定的重合采样点来解决此问题,相邻两帧的采样点分布可分别由式(3)和式(4)表示:

2)音频加窗。因为计算机只能处理有限长度的音频信号,所以需要把长时间序列的信号截断,获取音乐的时域信号。对音频信号使用长度相同且固定大小的窗口进行处理,从而得到等长且较短音频的信号。对分帧后的每一个帧信号Chunki通过加窗函数δ(n)进行加窗,通过增大音频信号中的高频分量的衰减以避免高频分量的影响,降低频谱能量泄露的风险[8],从而得到音乐的时域信号wi(n),通过加窗使每一帧的音频均映射在一段频谱中,用式(5)表示:

3)使用快速傅里叶变换(Fast-Fourier-Transform,FFT)对加窗分帧后的信号进行转换得到傅里叶频谱,wi(n)是输入信号w(n)的第i帧,Chunki是第i帧采样点的数量,FFT 可用式(6)表示如下:

通过FFT 处理后,将时域信号转换为频域信号,过滤了高于采样信号中最高频率的影响,同时实现了降维。
4)通过三角形滤波器组将能量谱定义在有M个滤波器的滤波器组中,设中心频率为f(m),m=1,2,3…,M,各区域的大小随m的值而变化,如图3所示。
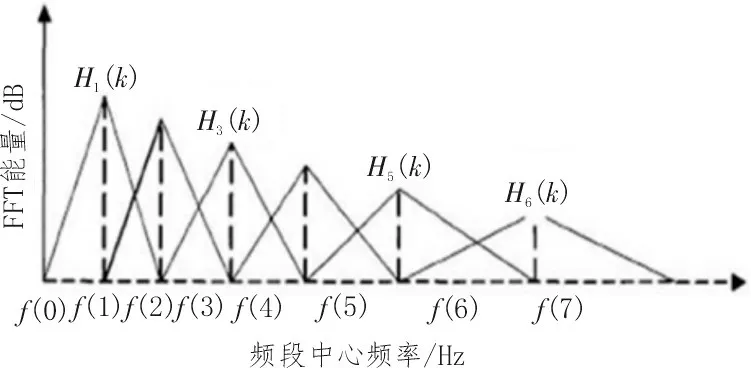
图3 梅尔频率滤波器组
三角滤波器的定义见式(7):

通过三角滤波器,实现了频谱的平滑化,强化了原信号中的共振峰,用较少的运算实现谐波消除[9]。
5)通过滤波器将实际频率f映射到梅尔频率Mel(f)中,以实现频率的统一化转变。将所有的滤波器输出进行对数运算,获取对数频谱,如式(8)所示,然后获取谱线能量的值。

数学信号频率与梅尔频率转换见图4。

图4 数学信号频率与梅尔频率转换
文中以GTZAN 数据集中的蓝调类型随机样本和流行类型随机样本为例,图5 和图6 分别描述了原始音频和梅尔频谱的对应关系。

图5 蓝调类别音频声谱图和梅尔频谱图

图6 流行类别音频声谱图和梅尔频谱图
6)对每一个对数运算结果进行离散余弦变换(Discrete Cosine Transform,DCT),由于滤波器通常都有交叠,因此滤波器能量彼此相关[10];DCT 需要对能量进行去相关性操作。
最终得到音频的梅尔倒谱系数特征MFCC 系数,如式(9)所示:

其中,i是音频信号,m表示滤波器个数,n为DOC(离散余弦先换)谱线。图7 为流行类型某样本的MFCC13 个特征层和20 个特征层的示例图。

图7 13个和20个特征层MFCC图例
2 多层卷积神经网络构建
项目中使用GTZAN 数据集进行音频分类研究。首先依次获取GTZAN 数据集的音频数据相应音频的MFCC 特征图谱,并对GTZAN 数据集中的数据添加one-hot 编码标签,通过深度卷积神经网络对模型进行训练,最终得到可用于音频分类的深度神经网络模型。
2.1 GTZAN数据集及标签编码
GTZAN 数据集是一个经典的音频数据集,具有十类音乐,分别为蓝调、经典、乡村、迪斯科、嘻哈、爵士、金属、流行、雷鬼乐及摇滚。每类音频都有100 个数据,每个数据时长均约30 s,采样率为22 050 Hz,包括16位单声道音频文件。
按照上述十类音频文件,对应进行one-hot编码。

表1 GTZAN数据集音频one-hot编码表
2.2 网络模型
卷积神经网络(Convolutional Neural Network,CNN)是一种前馈型神经网络,相比传统的神经网络,CNN 能有效减少数据前期的处理环节,具有准确度高、参数少等优点。文中使用深度卷积神经网络进行建模,使用了输入层、卷积层、池化层、全连接层以及输出层5 种层次机构。
1)输入层接收进入网络的数据,需设定输入的数据维度。该网络中的输入层接收标准化后的MFCC特征数据,按照预先设定好的采样率和采样点个数,以20 个特征层的MFCC 图谱作为输入数据。
2)卷积层用于提取数据特征。定义好卷积核的大小尺寸、深度、跨度后,也确定了卷积过程中的感受野和卷积运算的规则。卷积核在工作时,会有规律地扫过输入特征,在感受野内对输入特征作矩阵元素乘法求和并叠加偏差量[11],其计算公式为:

Zl和Zl+1分别表示第l+1 卷积层的输入向量和输出向量。i和j分别表示卷积过程中的动态区域,故有(i,j)∈{0,1,2…,L+1}。l+1 是Zl+1的尺寸。因为该项目实际使用二维卷积,所以有i、j两个参数。ωl+1表示第l层到第l+1 层的权重,b表示偏移量。
3)池化是在卷积运算之后,为了减少数据的冗余而进行的一种运算,从某种程度上来说,也是对卷积后数据的一种降维[12]。在一个小的区域内进行求均值或者求最大值等运算,该网络中使用的是Maxpooling 最大池化运算,如式(11)所示:

s0表示步长,则有当p→∞时,在池化过程中得到极大值,取得池化中的Maxpooling。
4)全连接层使用flatten 对多次卷积过的高维数据进行展开,使其满足全连接层的维度要求。然后使用全连接层,对数据进行降维处理[13]。
5)输出层输出十分类的一维向量。
文中使用的多层卷积神经网络结构如表2所示。

表2 多层卷积神经网络结构表
模型使用3×3 的卷积核,设定感受野的步长为(1,1),填充方式为等尺寸填充,根据模型设计,共有353 370 562 个参数。
2.3 激活函数和损失函数
1)在卷积层中,激活函数使用线性整流函数(Rectified Linear Unit,ReLU)进行工作,ReLU 又称修正线性单元[14],是一种人工神经网络中常用的激活函数,通常指代以斜坡函数及其变种为代表的非线性函数,其公式为:

其中,λ为反向传播的变量,当λ=0 时的ReLU函数图像如图8 所示。

图8 λ=0时的ReLU函数图像
2)输出层使用Softmax 函数进行分类。Softmax函数用于对输出向量中的各个元素求指数比值,从而计算出各个特征的概率分布[15],公式如下:

其中,i表示输出向量中的第i个元素,j表示向量的总长度,z表示向量小标对应的元素的值。
3)损失函数使用随机梯度下降法(Stochastic Gradient Descent,SGD)实现,SGD 本质上仍是一种梯度下降算法,最终目标是减少误差值[16],训练出最优参数。SGD 和最常用的GD 相比,GD 每一次迭代都是所有样本一起进行计算[17],而SGD 是随机获取批量样本中的一个进行计算[18],虽然会在局部出现震荡的现象,但是在总体上SGD 能实现快速收敛。
3 实验分析
文中使用GTZAN 数据集进行模型的训练和测试,将10 个类别的音乐(蓝调、经典、乡村、迪斯科、嘻哈、爵士、金属、流行、雷鬼乐及摇滚)进行整合,获取到1 000 个音频文件的数据集,然后对数据集的顺序随机排列。将上述随机排序过的数据集分为训练集、验证集和测试集,验证集在每个训练批次中随机加入进行训练,设置epoch 训练轮次为50 次,获取其最好的一次训练模型。
通过训练可发现,在第280 个样本处损失函数趋于稳定,但仍有小幅度下降,在第450 个样本处损失函数基本稳定在0.487 左右。损失函数随样本变化分布曲线变化情况见图9。

图9 损失函数随训练样本曲线变化图
随着损失函数的逐步下降,分类的准确率逐渐提升,图10 用val_acc 表示分类结果在验证集上的表现,acc 表示分类结果在测试集上的表现。同时,loss函数值在第450 个样本开始趋于稳定,所以仍按照500 个样本为例进行分析,验证集中准确率为92.1%,在测试集中准确率为86.3%,准确率变化曲线见图10。

图10 验证集和测试集中的准确率
4 结论
文中根据音频的特征,首先设计出提取音频梅尔倒谱频数的方案,提取出具有20 个特征层的梅尔倒谱频数,通过获取的数据作出每个音频文件的频数图谱。设计具有353 370 562 个参数深度为15 层的深层卷积神经网络模型,每个音频文件的频数图谱作为网络模型的输入数据,按照设定好的标签向量进行分类训练,训练结果在测试集中达到了86.3%。
因为数据集的数据类型较少,且数据集中的样本区分度低,所以在测试集和验证集中表现出来的差距较大。在模型的层级设计中,层级设计只用到了卷积层、池化层和全连接层,没有考虑过拟合等情况,所以使用其他数据集时,需要对模型层级进行调整,或者加入其他如Dropout 层消除过拟合等方式解决相应的问题。

