基于光纤弦测的无砟轨道变形监测关键技术研究
刘艳芬 柴雪松 冯毅杰 王智超 暴学志 时佳斌 凌烈鹏
1.中铁科学技术开发有限公司,北京 100081;2.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081
无砟轨道线路变形的检测手段以综合检测车和轮轨小车为主,但只能实现周期性检测,无法及时获取轨道板的变形状态。因此,亟待一种可靠的在线监测技术来及时掌握轨道板线形变化。分布式光纤传感技术具有测量范围长、抗电磁干扰、传感兼传输等特点[1],被广泛应用于地铁隧道及土木工程结构监测[2-3]、混凝土裂缝识别[4]、地质灾害监测[5]、高压输电线覆冰状态监测[6]、变压器绕组变形检测[7]等领域。文献[8]提出了分布式光纤传感技术在轨道板翘曲上拱监测中的应用方案,并试验验证了方案的可行性。
对于下部基础变化导致的轨道板变形,由于难以寻找保持不动的测量基准点,常规监测方法和技术无法实现监测目的。本文通过试验对传感光缆的特性及分布式光纤传感技术应用的关键参数进行研究,通过实尺模拟试验验证弦测分布式光纤传感监测方法在轨道板变形监测应用中的可行性,并对监测数据的稳定性、精度等进行分析。
1 检测原理
1.1 光纤布里渊散射原理
布里渊散射效应是光纤中注入的光波场与其中的弹性声波场相互耦合作用产生的一种非线性光散射现象。布里渊散射相对于入射光频率的变化量称为布里渊频移。基于布里渊散射的分布式光纤传感布里渊光时域分析(Brilouin Optical Time-Domain Analysis,BOTDA)的工作原理:处于光纤两端的可调谐激光器分别将一脉冲光和一连续光(分别称为泵浦光和探测光)注入传感光纤,当泵浦光和探测光的频率差与光纤中某区域的布里渊频移相等时,在该区就会产生布里渊放大效应,两光束之间发生能量转移。对两激光器的频率进行连续调节的同时,通过采集光纤一端射出的连续光的功率,就可以确定光纤在各小段区域内能量转移达到最大时所对应的频率差,从而得到关于应变、温度的分布消息,实现分布测量。BOTDA工作原理如图1所示。其中f0为脉冲波频率;fB为光纤固有布里渊频率;fB1为受到温度或应变反应后光纤的布里渊频率;f0+fB(fB1)为光纤中脉冲频率和布里渊频率的叠加连续波的频率。
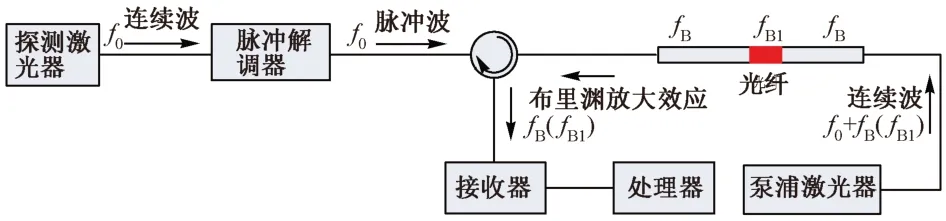
图1 BOTDA工作原理示意
布里渊频移、强度与光纤材料中的声速有关,声速受光纤材料的热光效应和弹光效应的影响,而热光效应和弹光效应与光纤材料的折射率、杨氏模量、泊松比和密度有关,所以光纤中温度和应变的变化都会引起布里渊频移的变化。光纤在温度T和应变ε下的布里渊频移fB(T,ε)及布里渊频移变化量Δf B(T,ε)的表达式为
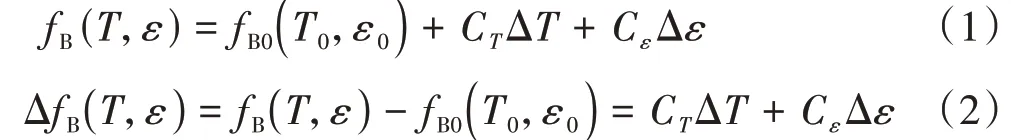
式中:fB0(T0,ε0)为光纤在初始温度T0和初始应变ε0下的布里渊频移;CT、Cε分别为布里渊频移的温度系数和应变系数;ΔT、Δε分别为光纤温度和应变的变化量。
从式(2)可以看出,当温度不变,只有应变引起布里渊频移时,布里渊频移变化量与应变变化量呈线性关系;当应变不变,只有温度引起布里渊频移时,布里渊频移变化量与温度变化量呈线性关系。
1.2 弦测原理
如图2所示,使用弦测分布式光纤传感监测方法对轨道板的变形进行监测时,首先将传感光缆按一定工艺布设于刚性弦测装置中,然后将刚性弦测装置的一端(E端)固定在道床板表面边缘,另一端(F端)放置于固定在轨道板表面的限位槽内,即E端同步于轨道板运动,F端在限位槽内滑动。光缆与轨道板固定于O点,转向固定装置安装于EF的中点D点。当轨道板发生横向位移时,F端会跟随轨道移动,转向固定装置会带动钢丝绳对传感光缆进行纵向拉伸,进而可以检测到轨道板的变形信号。

图2 弦测装置检测原理
已知OD=m。当弦测装置F端由A点移动到B点时,D点相应移动到C点。此时OC=n,F端的旋转角度为θ。计算OC与OD的长度差便可得出检测光纤的纵向拉伸位移Δl,表达式为

式中:h为轨道板横向位移。
由式(3)可以看出,光缆的纵向拉伸位移Δl与轨道板横向位移h、旋转角度θ有关,且随变量的增大而增大。当θ较小时,Δl≈h/2。可见,弦测装置可以检测出轨道板是否发生横向位移,且检测值约为轨道板横向位移的一半。
2 传感光缆特性
分布式光纤传感技术使用紧套光缆监测变形。传感光缆作为分布式光纤应用中的传感环节,其特性直接影响方案的实施效果。
2.1 传感光缆结构组成
选用的紧套光缆为单模石英光缆,从内到外依次为纤芯、包层、涂覆层和外套层[9]。其中光缆的主体结构光纤由纤芯和包层组成,纤芯的折射率较高,包层的折射率较低;涂覆层可以隔离杂散光;护套层可以提高光缆的强度进而对光缆起到保护作用。
2.2 传感光缆力学性能试验
使用分布式光纤传感技术时,传感光缆的抗拉强度、弹性模量、延伸率都是衡量检测能力的重要指标。使用万能材料试验机,采用单根传感光缆拉伸的试验方法测试传感光缆的力学性能。
光缆试样直径2.8 mm,初始标距为50 mm。对松弛状态的光缆施以一定的预加载,并以荷载反馈值大于0时所对应的位移作为位移0点进行光缆标距、荷载和位移的计算。
传感光缆拉伸应力σ、应变ε的计算式为

式中:F为拉伸荷载;S0为光缆截面积;L为光缆长度。
对试验数据进行处理,得出传感光缆拉伸加载试验结果,见图3。

图3 传感光缆拉伸加载试验结果
由图3可知:①F<50.05 N时,拉伸位移随拉伸荷载的增加而线性增加;F达到50.05 N,光缆发生塑性变形,此时光缆变形为3.5 mm;而后拉伸荷载基本保持不变,拉伸位移迅速增加。因此可以认为传感光缆的最大抗拉荷载为50.05 N,极限拉伸率为7.0%。②传感光缆的抗拉强度为8.2 GPa。③ε<0.01时,传感光缆的应变与拉伸位移的线性关系较好。④F=5.12 N时,拉伸荷载-应变曲线有突变,可能是光缆与夹具或夹具接触面的涂覆层变形破坏导致的;ε<0.01时,光缆的拉伸荷载和应变有较好的线性关系。
文献[10]对特殊光纤进行张拉极限试验,拉应变达到0.025时锚固装置坏掉但是光纤没有被拉断。因此,光纤的拉应变越大对锚固装置的要求就越高。工程中光纤的常规拉应变约0.01。
2.3 光纤光学性能
2.3.1 应变与频移的关系
利用布里渊散射识别光缆发生的应变或温度,实际上是识别光缆的布里渊频移。因此,获得光缆的应变与频移的关系尤为重要。
将标距330 mm的光缆布设到光学平台上,按步距0.1 mm(拉伸位移)进行逐级加载拉伸,拉伸位移达到1.0 mm时停止加载。分析逐级加载的应变和频移数据,得到光缆的应变与频移的数学关系,见表1。对光缆的拉伸位移-频移数据进行线性回归分析(图4),可见其线性回归度较好。

表1 不同位移下的应变系数

图4 拉伸位移-频移回归分析曲线
2.3.2 温度与频移的关系
将标距1 000 mm的光缆浸到水浴锅内,对水浴锅按约10℃级差逐级加热到100℃,分析逐级加热的温度和频移数据,得到光缆的温度-频移数学关系,即温度系数,见表2。可知,测量光缆的温度系数平均值为1.26 MHz/℃,比裸纤的温度系数1.20 MHz/℃略大。这是因为温度系数标定时将紧套光缆浸在水浴锅中,温度升高的过程中纤芯会受到紧套护套的张应变和压应变的影响,测量的温度系数会大于裸纤。
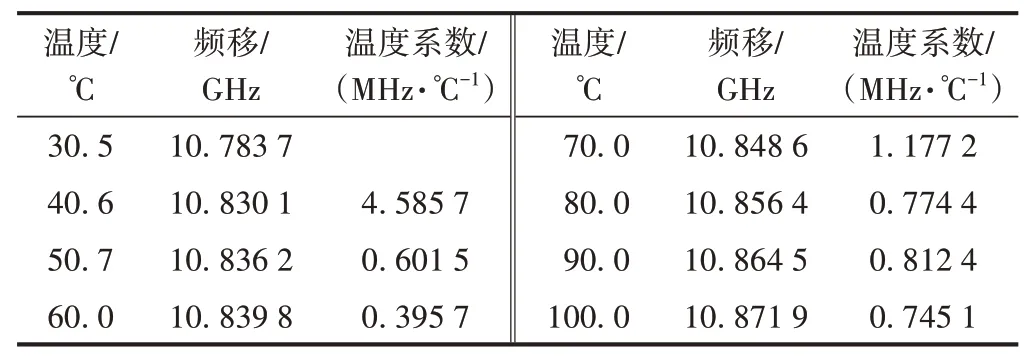
表2 不同温度下的温度系数
3 关键参数
3.1 空间分辨率
空间分辨率的大小直接影响采集数据的精度,空间分辨率越小采集精度就会越高。空间分辨率的选取还依赖测区长度、检测范围等参数。空间分辨率大于测区长度时,采集得到数据的误差会较大,所以空间分辨率应小于测区长度。空间分辨率与检测范围的关系取决于选用的分布式光纤传感解调仪参数,如Ozoptic公司解调仪50、100 cm空间分辨率的理论检测范围分别是5、10 km。
通过室内模拟试验探讨同时满足测区长度和检测范围要求的空间分辨率选取方法。
将长度为3 km的传感传输光缆接入分布式光纤传感解调仪,选取标距150 cm的光缆布设在光学平台上,对测区内的光缆按步距0.5 mm(拉伸位移)进行逐级加载拉伸,拉伸位移达10.0 mm时停止加载。使用50、100 cm空间分辨率各采集若干组数据。
根据两种空间分辨率采集的应变数据,拟合得到应变-拉伸位移的线性回归关系(图5)。利用线性回归方程反算得到不同拉伸位移下的计算应变,然后对采集应变数据和计算应变数据的误差进行统计分析,得到应变数据的误差分布,见图6。可知,50、100 cm空间分辨率的均值分别为56.625 7、48.324 9,均方差分别为24.916 1、19.142 4。显然,在测区长度和检测范围都适用的条件下,100 cm空间分辨率采集数据的稳定性更好。这是因为100 cm空间分辨率的脉冲光含有的能量和信噪比较高,即空间分辨率越小,脉冲光中含有的能量越小,信噪比越差。
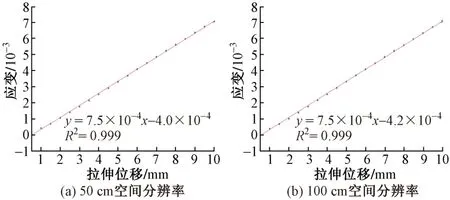
图5 两种空间分辨率采集的应变数据及拟合结果
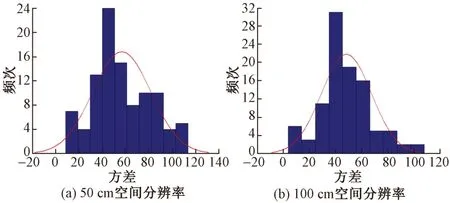
图6 两种空间分辨率采集的应变数据误差分布
因此,空间分辨率的选取不仅要考虑采集精度,还要考虑采集数据的稳定性,要根据工程数据精度和稳定性的要求进行选取。
3.2 测区定位和测点设置
使用弦测分布式光纤传感监测方法对无砟轨道变形监测时,需要根据频率曲线的波形特点定位测区和识别测区内部监测点位。根据监测频率曲线半宽全峰的起止点对测区的起点、终点进行定位。根据频谱数据点的洛伦兹拟合曲线波峰的数量,对测区监测点位进行识别。
测区长度是频率曲线的半宽全峰(Full Width at Half Maxima,FWHM)长度。过波峰幅值中点作平行于峰底的直线,与曲线相交两点之间的距离即测区长度。如图7所示,交点X1、X2便是测区的起点和终点。
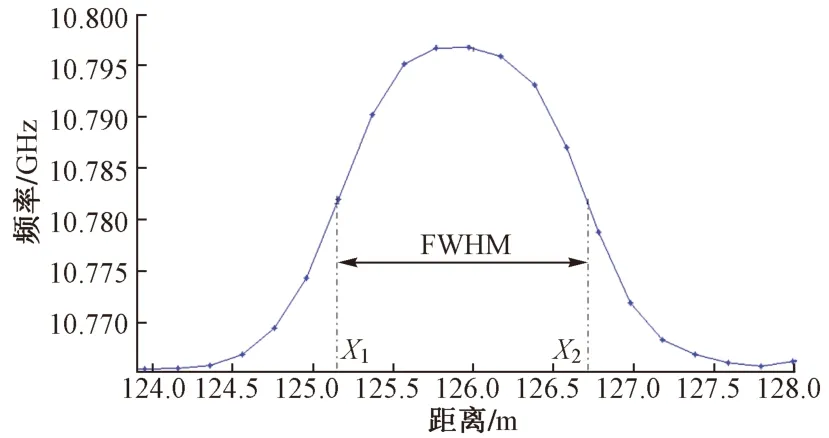
图7 测区的起点和终点定位
监测区域内的光缆因外部张力或温度变化产生应变时,锚固区附近监测光缆的受力比较复杂,监测的应变数据不仅包括目标监测应变数据,还包括锚固件与光缆之间相互作用产生的拉压应变。因此,锚固区附近的监测点不能作为测区的监测点。
对锚固区附近和测区内部监测点的频谱数据进行分析发现,锚固区附近监测点的频谱数据有双峰,测区内部监测点的频谱数据有单峰,如图8所示。对频谱数据按一定规则进行洛伦兹曲线和改进的洛伦兹曲线拟合,根据每个测点频谱数据的洛伦兹拟合曲线中出现的波峰数量以及每个波峰的跨度和幅值所占的比例,对该点是否可以作为监测点进行评估。

图8 锚固区附近和测区内部监测点频谱数据及拟合结果
4 传感光缆的布设工艺
4.1 黏合材料的选取
为研究道床板表面布设传感光缆及弦测法光缆端部固定方式,使用多种胶黏剂作为光缆固定的黏合材料。结合实验室环境,将光缆粘接于混凝土板表面,固化后对光缆进行张拉。
通过对胶黏剂进行优选及在原材料基础上进行设计,选取10种胶黏剂作为光缆黏合材料。养护方式均为室温养护。测试结果见表3。可知,10种胶黏剂粘接效果良好;对光缆进行张拉时,随着荷载增大,大部分胶体与光缆发生脱离,甚至出现被抽出的现象;对以丙烯酸酯固化胶作为胶黏剂的光缆进行张拉时,直至光缆拉断也未脱离出胶体,满足监测方案需求,丙烯酸酯固化胶可作为光缆优选粘接材料。
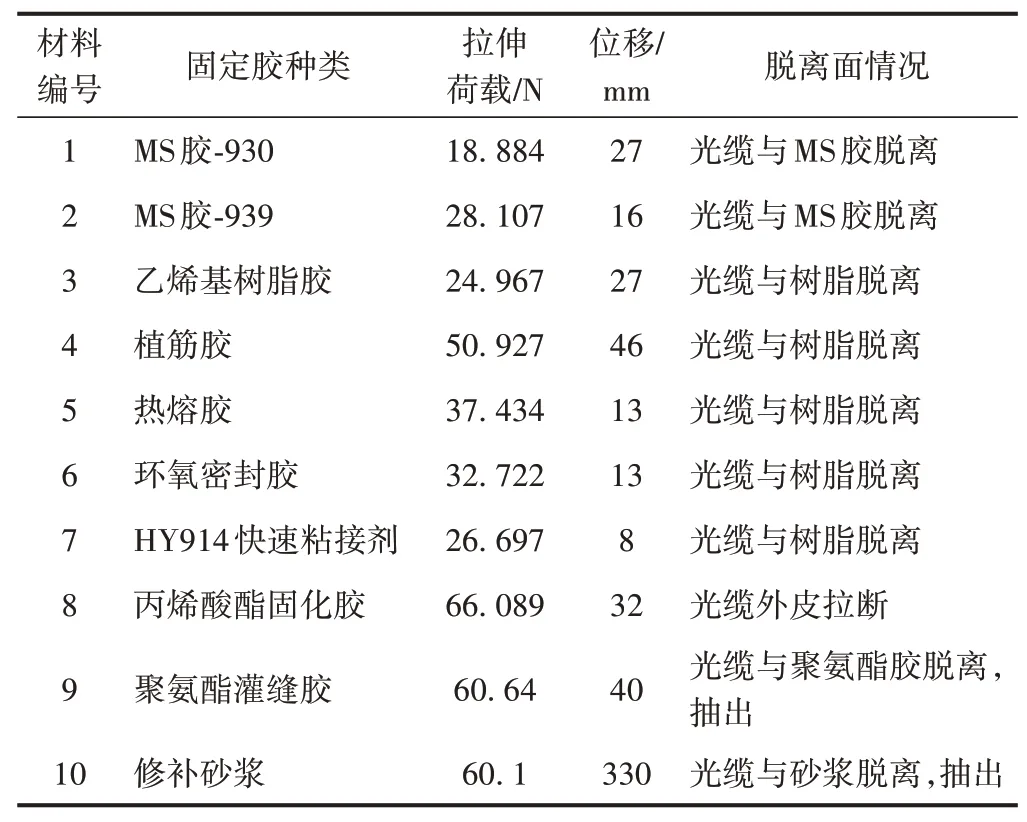
表3 10种胶黏剂光缆粘接效果对比
4.2 布设方式
传感光缆的布设方式一般有植入式、定点式两种。植入式是将传感光缆植入被测对象体内或通过胶黏剂在被测物体全覆盖粘贴,使传感光缆与被测物体同步变形,达到变形监测的目的。定点式是在被测对象上通过膨胀固定、注胶固定、器件固定等方法,每隔一定距离固定传感光缆,通过固定点间光缆的应变来测量被测对象的变形情况。定点式布设方法具有施工简单、维护方便、测试量程大、变形值方便量化等特点[5],选用定点式方法布设光缆。
5 试验分析
5.1 试验场地
在工务工程技术创新试验基地内进行实尺模拟试验。试验基地内包含CRTSⅠ型板式、CRTSⅡ型板式、CRTSⅢ型板式、CRTSⅠ型双块式等多种无砟轨道结构实尺模型,总长度约200 m。
5.2 试验工况
在CRTSⅠ型板东侧上表面边缘安装弦测装置,装置覆盖5块轨道板,利用轨道精调装置对2#、3#、4#轨道板进行横向推动。设单块轨道板南侧为S,北侧为N。在N2、S3、N3、S4位置安装百分表控制推动位移,在弦测装置正矢对应轨道板位置加装百分表进行辅助测量,其中位置②与N2共用一个百分表,位置④与N3共用一个百分表,如图9所示。试验中设置5种工况,如图10所示。

图9 实尺模拟试验百分表位置
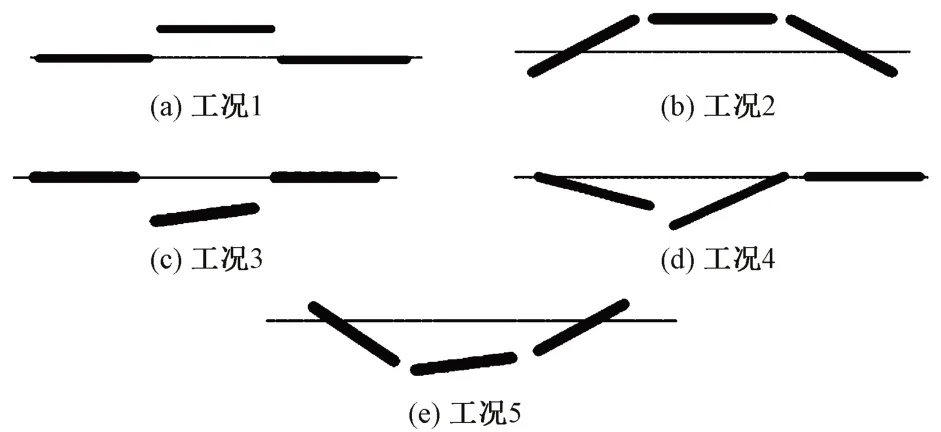
图10 试验工况示意
工况1:单板等量平推。模拟3#轨道板横向移动,S3、N3位置同向等量平推,通过S3、N3位置的百分表控制推板位移。轨道板先向西平推,每次平推位移分别是2、4、6、8、10 mm,重复3次;然后向东平推,平推量和次数与向西一致。共推板30次。
工况2:三板等量平推。对2#、3#、4#轨道板进行横推加载,N2、S3、N3、S4位置同向等量平推,保证N2、S3同时推动,N3、S4同时推动,通过N2、S3、N3、S4位置的百分表控制推板位移。轨道板先向西平推,每次平推位移分别是4、6、8、10、12、14、16 mm,重复3次;然后向东平推,平推量和次数与向西一致。共推板42次。
工况3:单板不等量平推。模拟3#轨道板横向移动,S3、N3位置交替增加推板位移,通过S3、N3位置的百分表控制推板位移,先南(S3)后北(N3)和先北(N3)后南(S3),先推动端的位移按2 mm变化量从2 mm增加到10 mm,后推动端的位移也按2 mm变化量从0增加到10 mm,重复3次。共推板60次。
工况4:双板平斜推。模拟2#、3#轨道板横向移动,S3、N2位置交替增加推板位移,通过S3、N2位置的百分表控制推板位移,先南(N2)后北(S3)和先北(S3)后南(N2),推板方法同工况3,共推板60次。
工况5:三板不等量平斜推。对2#、3#、4#轨道板进行横推加载,N2、S3和N3、S4位置交替增加推板位移,保证N2、S3同时推动,N3、S4同时推动,通过N2、S3、N3、S4位置的百分表控制推板位移,先南(N2、S3)后北(N3、S4)和先北(N3、S4)后南(N2、S3)。先推动端的位移按4 mm的变化量从4 mm增加到20 mm,后推动端的位移也按4 mm的变化量从0增加到20 mm,重复4次,共推板80次。
5.3 数据分析
汇总5种工况试验结果,计算各种工况下轨道板变形的测量值和真实值的误差,统计得到误差的最大值、最小值、均值、均方差以及误差在-1.5~1.5 mm内的占比P,结果见表4。可知,5种工况的误差在-1.5~1.5 mm内的占比平均为93.57%,说明方法可行。
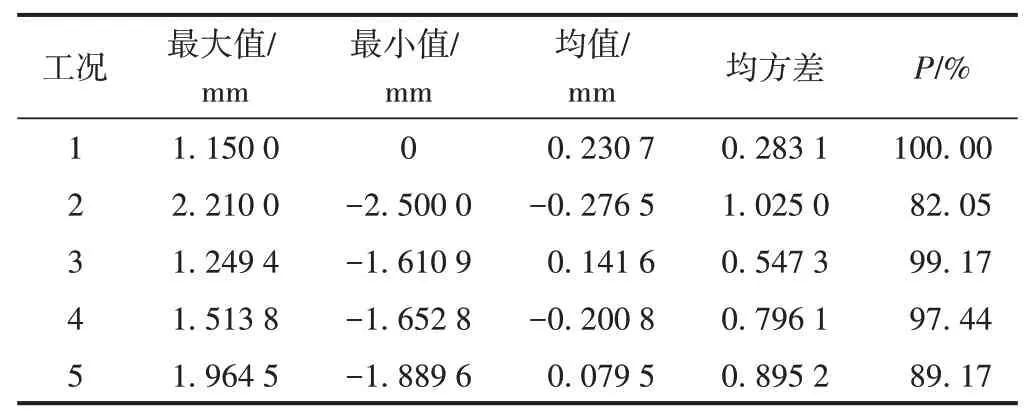
表4 5种工况误差分布统计结果
6 结论
1)使用频率数据点频谱数据洛伦兹拟合曲线单双峰判断的方法,可以快速有效地评估各监测点监测数据的可信度。
2)空间分辨率越高,脉冲光的信噪比就越低,抗干扰能力相对就越差。
3)使用弦测分布式光纤传感监测方法对轨道板变形进行监测的误差在-1.5~1.5 mm内的占比平均达93.57%,说明该方法可行。

