正交匹配追踪算法的优化及FPGA实现
张金鹏,钱 慧,王仁平
(福州大学 物理与信息工程学院,福州 350116)
1 引 言
压缩感知(Compressed Sensing,CS)[1,2]是近十多年来信号处理领域最著名的研究进展之一.CS主要由压缩投影和重构两个步骤组成.在压缩投影阶段,利用稀疏基和观测矩阵构建CS矩阵,将稀疏信号在CS矩阵中进行投影,获得信号的观测向量.在重构阶段,CS通过贪婪追踪、凸优化等方法从观测向量中重构出原始信号.这些CS重构算法以非线性计算为基础,是典型的计算密集型算法.在早期CS系统中,一般通过离线计算重构原始样本.但是随着物联网、人工智能技术的发展,便携式应用逐渐普及,实现CS快速重构成为研究领域的关注重点[3].
正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)[4,5]是CS系统中讨论最广泛的重构算法之一.近几年,研究学者对面向OMP算法的硬件加速计算进行了大量的研究.文献[6-10]使用改进的Cholesky分解算法优化最小二乘(Least Squares,LS)问题,避免了平方根运算,减少了计算延时.其中在文献[6]中提出了第一个OMP算法的硬件实现设计,获得了比CPU和GPU[11]更快的重构速度.文献[7]提出了一个新的高度流水线化的OMP硬件实现架构,通过适当水平的展开最大化并行度,通过共享硬件降低资源使用量.文献[12,13]使用的是QR分解算法实现最小二乘求解.其中文献[12]中使用了一种基于改进的Gram-Schmidt算法的增量式QR分解算法优化LS问题,通过每次迭代只更新Q矩阵和R矩阵的一列减少了存储资源消耗,并设计了一种高并行度的硬件架构,该架构的硬件复杂度几乎不受稀疏度的影响.文献[13]提出了一种无方根增量式QR分解算法,进一步消除了平方根操作,转换为一些更简单的操作,降低了计算的复杂度.另外文献[14-16]使用了一种矩阵求逆旁路(Matrix inversion bypass,MIB)技术,通过分解矩阵求逆的过程有效降低了算法的计算复杂度.上述方法都是针对LS问题优化算法,然后用硬件实现加速重构,获得了一定的加速效果,但是重构速度会随着迭代次数的增加而迅速降低.
从减少矩阵求逆次数的角度出发,本文提出了一种近似OMP重构算法.在前K-1次迭代中用最大值计算方法近似替代LS计算去索引最大列,只在第K次迭代时进行LS计算重构原始信号估计值,仅需要做一次矩阵求逆计算.设计了一个近似OMP算法的硬件实现架构,主要包含计算模块、存储模块和控制模块3个部分.该架构用Verilog HDL语言进行描述,在Xilinx公司的Vivado软件上进行综合仿真实验.实验结果表明,本文设计的硬件架构重构速度快同时具备一定的可扩展性.
2 正交匹配追踪算法及近似实现
2.1 正交匹配追踪算法
OMP算法基本思想是在每次迭代中,通过计算当前残差和CS矩阵的内积值找到CS矩阵里与当前残差最匹配的一列,然后通过去掉这一列的贡献计算一个新的残差,通过迭代计算最后输出原始信号的估计值.OMP算法流程如下:
输入:CS矩阵A=ΦΨ,随机解调架构矩阵Φ∈RM×N,傅里叶变换基Ψ∈RN×N,观测向量y∈RM,稀疏度为K;
初始化:迭代次数t=1,支撑索引集Λ为空集,r0=y;
迭代过程:
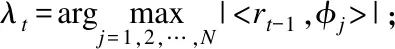
2.更新索引集Λt=Λt-1∪λt,更新原子集At=At∪φλt;
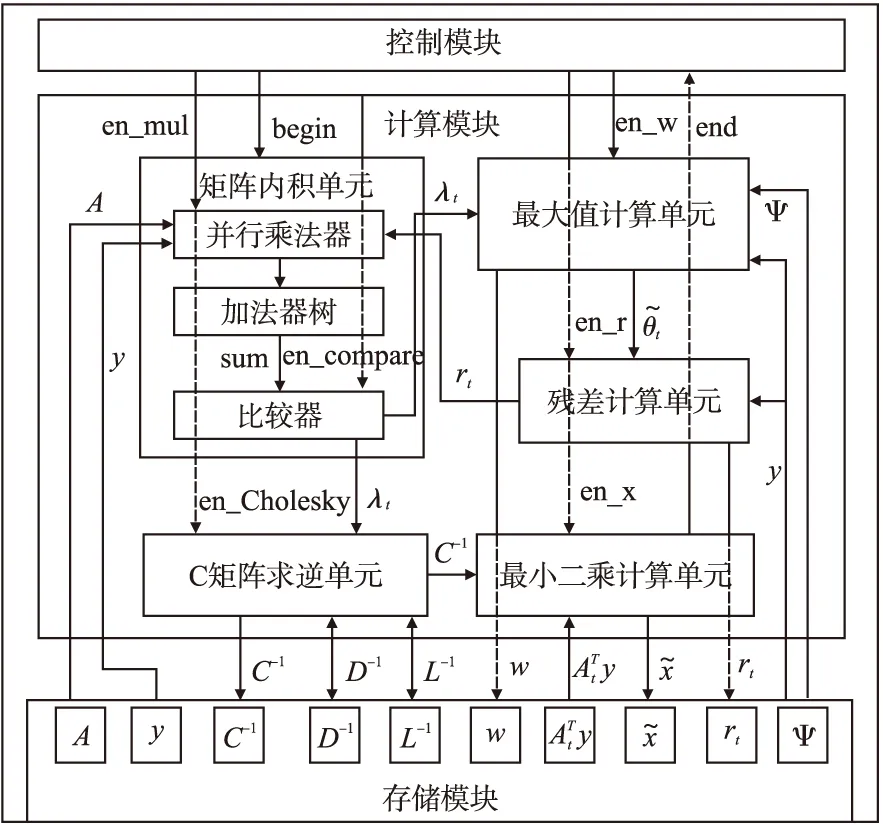
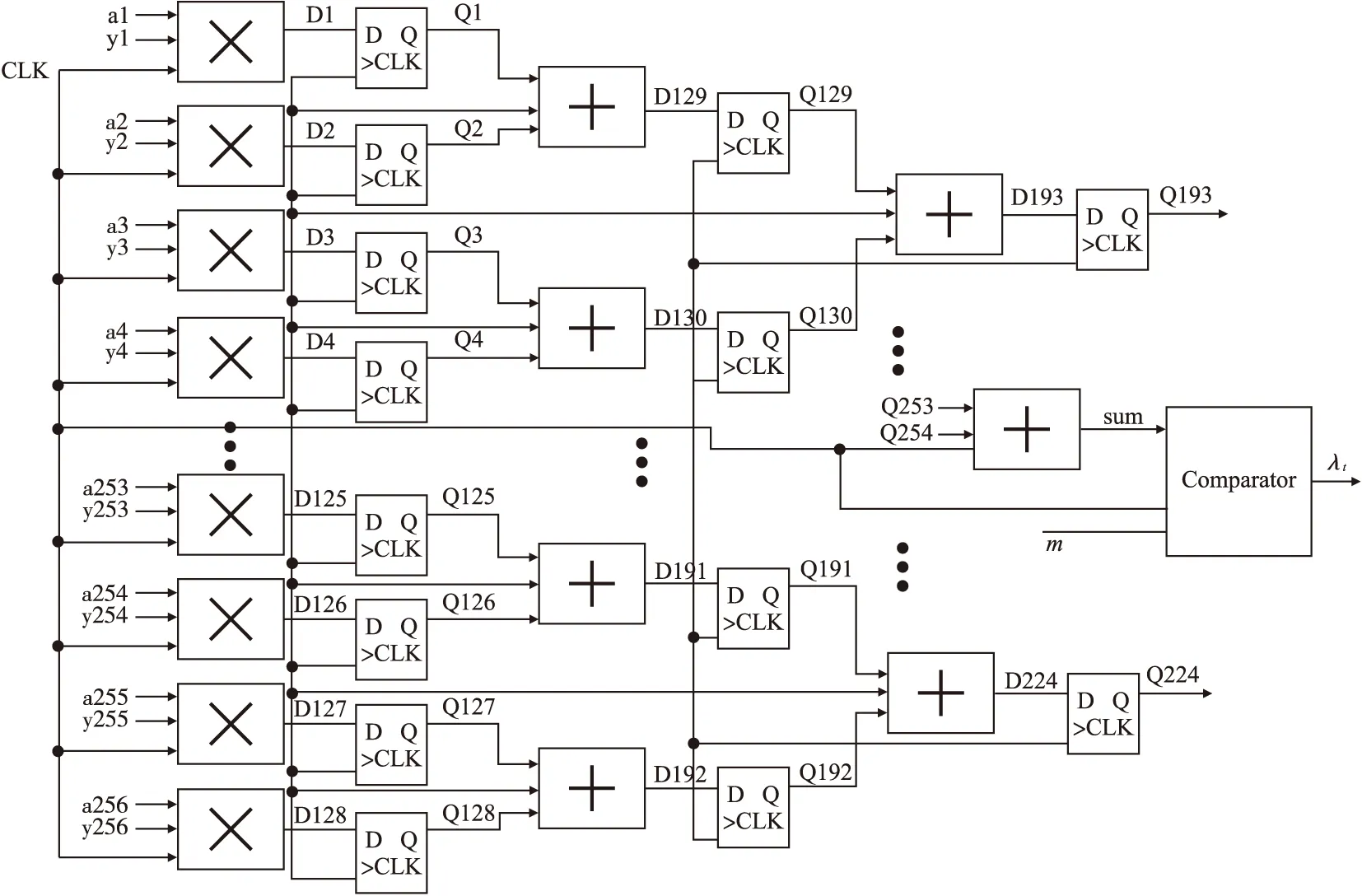
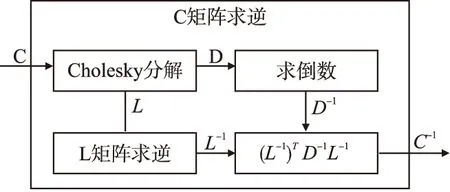
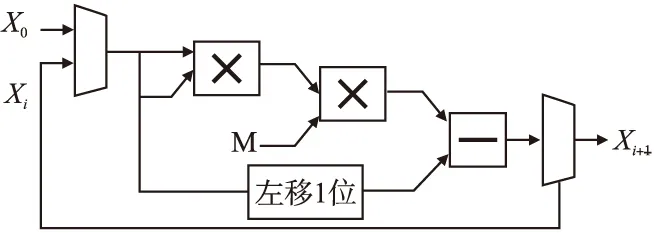
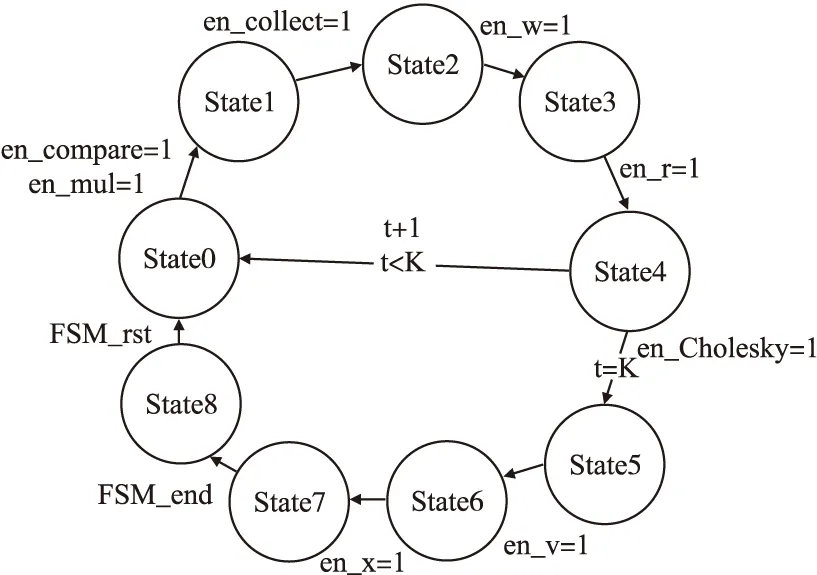
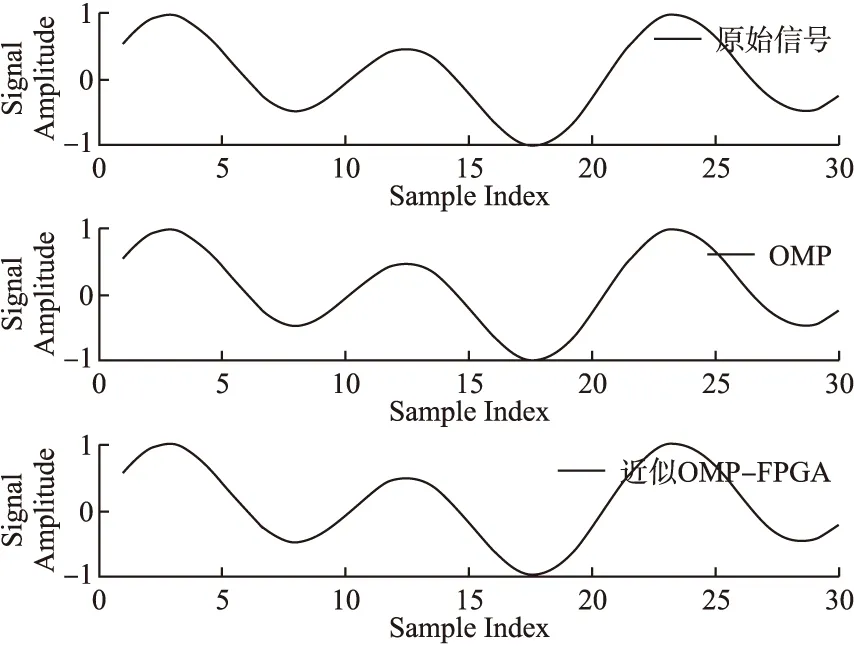
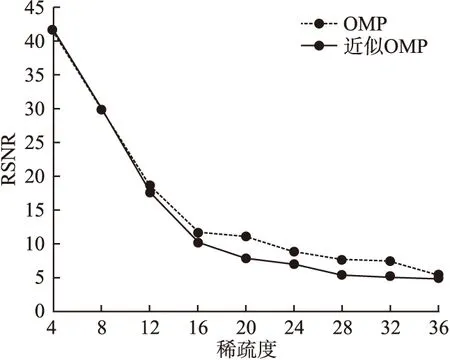
5.判断,若迭代次数t 输入:CS矩阵A=ΦΨ,随机解调架构矩阵Φ∈RM×N,傅里叶变换基Ψ∈RN×N,观测向量y∈RM,稀疏度为K; 初始化:迭代次数t=1,支撑索引集Λ为空集,r0=y; 迭代过程: 5.判断,若迭代次数t C=LDLT (1) 其中L是对角线元素为1的下三角矩阵,D是对角矩阵,按以下公式计算求出C-1: (2) (3) (4) C-1=(L-1)TD-1L-1 (5) 矩阵D-1可以通过将矩阵D对角线上的元素求倒数获得. 本文在MATLAB中进行近似OMP算法的仿真验证.原始信号是由两个不同频率的正弦波相加得到的,一个正弦波的频率从20Hz增加到119Hz,另一个从150Hz增加到159Hz,步进都是1,两个信号可以组合出1000个样本,这1000个样本有4000个最大列,经过仿真验证,近似OMP算法找对了全部的最大列并成功重构原始信号,验证了近似OMP算法的可行性. 算法整体硬件架构如图1所示,主要分为计算模块、存储模块和控制模块.计算模块完成算法迭代过程中的所有运算,比如矩阵内积、最大值计算、残差计算、矩阵求逆的运算等等.存储模块用来存储所有的矩阵、向量和数据.控制模块负责控制算法的各个状态的转换以及从存储模块中读取相应的数据到计算模块中和将结果写回到存储模块中. 图1 近似OMP算法硬件架构Fig.1 Structure of approximate OMP algorithm 计算模块又分为矩阵内积单元、最大值计算单元、残差计算单元、C矩阵求逆单元和最小二乘计算单元. 3.2.1 矩阵内积单元 矩阵内积单元由256个复数乘法器构成的并行乘法器和255个复数加法器构成的加法器树和一个比较器组成.一个复数乘法器通过调用4个DSP资源实现,总共调用了1024个DSP资源.加法器通过调用slices资源实现.每个周期从存储模块中读取A的一列和y或(r)进行内积操作,结果送入到比较器进行比较,并记录较大列的列序号.最终在比较完所有列的内积后,输出内积值最大的列的列序号.硬件架构如图2所示.最大值计算单元、残差计算单元和最小二乘计算单元的大部分运算都可以复用这里的并行乘法器和加法器树结构实现,从而降低硬件资源使用量. 图2 矩阵内积单元架构Fig.2 Structure of matrix inner product unit 3.2.2C矩阵求逆单元 矩阵C和C-1是正定对称矩阵,只需要求出C-1对角线上的元素和下三角部分的元素.首先需要根据公式(2)和公式(3)求出L矩阵和D矩阵的元素.其中L是对角线元素为1的下三角矩阵,D是对角矩阵.然后L矩阵和D矩阵分别求逆,最后利用公式(5)求出C-1.硬件实现架构如图3所示. 图3 C矩阵求逆单元架构Fig.3 Structure of C matrix inversion unit 在求矩阵D-1的元素时涉及到除法,本文选用的是比较经典的牛顿-拉夫森方法求倒数.该方法是找到一个在零点有解X=1/M的函数f(X),一般这个函数如式(6)所示: f(X)=1/X-M (6) 这个函数在零点的解就是M的倒数.牛顿-拉夫森方法给出了迭代公式: (7) 根据文献[7]中确定的初始值X0=3-2M,利用公式(7)进行迭代计算,Xi的值就会收敛于M的倒数.用这种方法将除法运算转化成了乘法和减法运算.硬件实现架构如图4. 图4 牛顿-拉夫森求倒数硬件架构Fig.4 Structure of Newton-Raphson inversion 然后利用公式(4)求L-1矩阵的元素.最后可以根据公式(5)计算矩阵C-1.如果想要设计能重构稀疏度更高的信号的硬件架构,只需要修改最小二乘单元的硬件架构,而不需要改变其它部分的硬件架构,具有一定的可扩展性. 存储模块主要用来存储算法计算所需要的数据,包括CS矩阵、观测向量、稀疏基、残差等和从计算模块写回的各种数据.各个数据的存储具体情况如表1所示.为了能够在一个周期读出矩阵一列的数据并行的送入到并行乘法器中,本文将矩阵一列的数据存在BRAM同一个地址中.其中CS矩阵A用单独的一块BRAM存储,地址是0到1023,傅里叶变换基Ψ用单独的一块BRAM存储,地址是0到1023,观测向量y和残差r存储到相同的一块BRAM中,观测向量存到0地址,残差r按迭代顺序存在y向量后面.本文设计的架构比其它相似设计多存储了一个傅里叶变换基Ψ,所以消耗的BRAM资源会多一些. 表1 内存资源使用情况Table 1 Memory resources usage 控制模块主要通过状态机完成对各个运算子模块工作条件的控制.状态机的状态转换图见图5,各状态说明如表2所示.每个子模块都有一个控制信号,在子模块需要工作的时候状态机将该子模块的控制信号置1,当任务完成时,子模块反馈给控制模块一个信号,然后状态机将该子模块的控制信号置0,进入下一个状态.当迭代次数t 图5 状态转换图Fig.5 Diagram of FSM 表2 状态机的各状态说明Table 2 Description of FSM 本文实验步骤如下:1)输入原始信号f由两个频率分别为50Hz和100Hz,幅值分别0.3和0.6的正弦波相加得到,采样序列1:1024,采样频率为1024,然后对原始信号f进行归一化处理;2)在MALTAB中运行近似OMP算法程序,获得CS矩阵A,傅里叶变换基Ψ,观测向量y的原始数据,并对数据进行定点量化处理;3)将得到的数据导入coe格式文件,在Xilinx公司的开发工具Vivado 2016.2中进行仿真测试;4)将FPGA中仿真得到的结果导入MATLAB中,在MATLAB中进行反傅里叶变换得到重构信号,并与原始信号进行对比,验证是否重构成功. 当K=4时,近似OMP算法在FPGA中输出原始信号在频域的值,是放大了2^5倍的定点数据,分别为235-305i、214+308i、57+176i、58-168i,对应的在MATLAB中仿真的数据是209-300i、210+301i、55+173i、54-169i.图6是K=4时的仿真结果,依次为:原始信号、在MATLAB中用经典的OMP算法重构的信号、近似OMP算法在FPGA中的输出结果重构的信号. 图6 重构结果图Fig.6 Diagram of reconstruction results 本文用重构信噪比(recovery signal-to-noise ratio,RSNR)对重构误差进行分析,公式如下: (8) 图7 RSNR曲线图Fig.7 Curve of RSNR 在表3中列出了与其它相似设计比较的具体情况.本文的稀疏基是傅里叶变换基,因此设计的是复数硬件架构,在矩阵内积模块本文调用了1024个DSP资源实现复数并行乘法器,降低了slices资源的使用量.由于需要存储额外的傅里叶变换基,增加了BRAM资源的使用量.对比稀疏度K=36时的重构时间,本文的重构速度快了1.25-1.72倍. 表3 实现结果与其它相似设计的比较Table 3 Comparison of implementation results with other similar existing designs 本文提出了一个新的近似OMP算法,从优化算法的最小二乘问题角度出发,使算法只需在第K次迭代时进行最小二乘计算重构原始信号估计值.在其它K-1次迭代中用最大值计算方法替代最小二乘计算去索引最大列,从而减少了矩阵求逆的次数.设计了近似OMP算法的硬件实现架构主要包含计算模块,存储模块和控制模块3个部分.该架构用Verilog HDL语言进行描述,在Xilinx公司的Vivado软件上进行综合仿真实验.对比现有相似实现设计,本文设计的架构通过调用更多的DSP资源减少了slices资源的使用量,在208MHz频率下重构速度提升了1.25-1.72倍,同时具备一定的可扩展性.2.2 近似正交匹配追踪算法




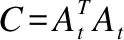
3 硬件系统设计
3.1 整体架构
3.2 计算模块
3.3 存储模块

3.4 控制模块

4 实验结果与分析
4.1 实验结果
4.2 分析比较

5 结 论

