移动众包环境下一种多阶段质量感知的在线激励机制
高丽萍,孙明达,高 丽,陈庆奎
1(上海理工大学 光电信息与计算机工程学院,上海 200093)
2(复旦大学 上海数据科学重点实验室,上海 200093)
3(上海理工大学 图书馆,上海 200093)
1 引 言
通信技术和移动智能终端的发展让移动设备能够采集到多种传感数据,这使得智能手机用户能够轻松发现并分享数据.于是移动众包(MCS)成为了一个热门话题,其融合了智能手机和众包的特点,利用广大的移动用户群体来分享信息,提高社会福利.同时,MCS可以结合云服务,物联网等前沿技术,使其在物流运输,环境监控,社交网络等各个领域被广泛运用[1,2].
一个典型的移动众包应用主要基于3类实体,任务请求者、任务参与者(简称工人)和众包平台.请求者将一些感知任务发布到平台上,并设置一些要求(预算,截止时间等).对任务感兴趣的工人向平台提出执行任务的请求,平台收集到工人信息后合理地分配任务.最后根据工人的任务完成情况,平台给予其一些回馈.由于众包工人来源于互联网,存在较多不确定因素,工人持续提交低质量感知数据会影响MCS平台的可靠性和精确性,损害请求者的利益.如何有效地激励工人参与任务并且得到高质量的传感数据成为MCS的核心问题.
因此,一个可靠的MCS平台需要设计有效的激励机制[3].许多激励机制建立在金钱激励上,即每个工人对任务有一个报价,表示他所消耗的物质资源或所提供劳动力的货币价值,并期望自己的贡献能够获得回报.如果没有足够的奖励,工人就没有动力参与任务.平台根据报价和工人其余信息来决定任务的分配和报酬.在离线场景下,平台先收集所有工人的信息后再进行调度分配,这使得平台比较容易针对不同的目标(如最大化效用[3-6]、最大化社会福利[7-9]、最小化报酬[10,11]),配合一些限制条件选择最优的工人集.然而在现实中,工人是以随机动态的方式到达或离开平台.与离线场景相比,MCS平台在在线场景中无法事先得知工人会在什么时间段参与任务.一旦工人上线,需要立即做抉择,即是否接受或拒绝工人的请求,同时当任务分配给工人后,还需要根据已有的信息决定报酬.
此外,激励机制的设计还需考虑质量评估.MCS的任务大多以提交传感数据为主,如监测某个地区的噪声、温度、路面状况等.由于传感器和动态环境的不一致,移动用户采集的传感数据通常存在噪声或不同程度的误差.在无法准确了解每个工人的感知行为和任务地点的真实情况下,平台很难去判断传感数据的质量.同时在MCS应用中,获取真实的样本数据(Ground Truth)作为其它传感数据的质量标准是困难的,在很多情况下甚至是不现实的[4].这时候,平台可以先发布一些任务,采集足够多的历史数据后判断数据质量,推测出每个工人的可靠程度.但是请求者有固定的预算,这限制了平台不能无限次分配任务来获取大量历史数据.所以MCS的激励机制需要制定一个有效的质量评估方式.
本文之前的工作[5]提出了一种长时间质量感知的激励机制策略(QAI),将众包任务分配过程分成多个阶段,同时把工人的质量看作是隐变量,各个阶段的请求者都会给工人提交的答案进行打分,平台则根据这些分数运用隐马尔可夫模型来预测下一阶段的工人质量.然而,QAI是一个离线场景下的激励机制,同时假设了请求者可以直接评估工人的任务结果,无法解决前面提到的问题.因此,本文在QAI的基础上进一步考虑在线工人选择问题,提出一种多阶段质量感知的在线激励机制(SQOI).具体的贡献如下:
·本文考虑了预算与时间约束下的在线工人选择问题,将众包活动周期分成多个阶段,设计了阶段性的系统与质量模型,通过静态质量和动态质量来评定各个阶段在线工人的服务质量.
·根据模型,提出多阶段质量感知的在线激励机制SQOI,设计了具体的框架,集成了阶段性工人选择、质量预估和参数更新三个模块.理论证明了SQOI具有预算可行性、个体合理性、真实性和计算效率.
·通过实验测试了SQOI在不同参数下的性能,并且证明了SQOI在提升数据质量上的有效性.
论文的其余部分组织如下:第2节对相关工作进行了介绍.第3节介绍了系统模型和效用计算.第4节给出了多阶段质量感知的在线激励机制框架和相关算法设计.第5节对SQOI进行了仿真实验.结论在最后一节中给出.
2 相关工作
2.1 激励机制
如今,已有许多关于MCS的激励机制研究.大多数的工作是针对离线场景下的激励机制,即平台在分配之前就得到了工人与任务的所有信息,如工人的能力,偏好,报价等.同时平台会指定某一目标,这样工人的选择问题变为了在特定约束下的规划问题,需要设计算法求解该问题.如Yang等人[3]运用Stackelberg博弈思想设计激励机制,最大化用户的效用.Peng等人[6]从提高传感数据质量的角度上设计激励机制,并运用信息论度量每个参与者的有效数据贡献.Wen等人[7]提出一种基于质量驱动的拍卖激励机制,并提出一种概率方案来评估数据的准确性.Jin等人[8]则将用户信息质量作为激励机制的一个重要指标,同时将任务分配问题看作一种集合覆盖问题,设计了一种组合的反向拍卖模型来提高社会福利.以上研究都是基于离线场景下,不适用于工人实时到达的在线场景.
当前也有一些关于众包的在线场景研究.Singer等人[10]提出了一种竞价模型,从预算范围内最大化任务数量和最小化支付报酬两种目标考虑激励相容机制的实现.Zhao 等人[12]基于在线竞价模型,研究在指定预算下的服务价值最大化问题.同时在文献[11]以最小化MCS的任务报酬为目标设计了节俭式的在线激励机制.一些研究[9,13-15]将经典的多臂赌博机模型用在移动众包的在线任务分配中.其主要思想是以在线学习的方式权衡众包环境下未知工人的探索与利用,在分配任务的过程,逐步对每个工人的能力和偏好有全面的认知.其中文献[9,13]在工人选择上进一步考虑其上下文信息,对工人的服务质量进行建模,尽可能地选取高质量工人.Han等人[14]提出BLISS框架来解决有限预算下的最大化传感收益问题.Gao等人[15]则考虑预算和覆盖限制下工人招募问题,从招募成本同质和异质两种情况进行研究.然而以上的研究都假设了工人的数据质量或贡献可以直接得到.
2.2 数据质量评估
由于在很多众包场景下,任务请求者需要由第三方平台为其判断工人提交的数据质量,甚至为每个任务集成一个可靠准确的答案,因此众包的质量评估成为了研究的热点.Hung 等人[16]采用了多数投票算法,任务分配给多个工人独立完成,平台将收集的数据中的多数意见作为最终的正确结果.这个方法将所有工人的感知数据在质量和贡献上视为平等,没有考虑工人的多样性,最终的结果往往不准确.Zhang等人[17]则在标签收集任务中,将工人执行不同类别任务的可靠性作为权重,设置加权多数投票算法,得到每个任务的真实标签.然而其考虑的任务是基于二进制标签,不适用于连续性的移动传感数据.同样Liu等人[18]采用MAB模型来提升数据集标记任务的质量,其评估结果是离散的.Li 等人[19]进一步使用迭代式加权多数投票算法来减少标签聚合的错误率.Liu等人[4]研究了感知上下文与数据质量的关系,通过构建一个上下文数据质量分类器来实时估计工人数据质量.Yang等人[20]通过无监督学习的方式,将传感数据聚类成多个中心,测量每个用户的数据与中心的偏离值作为其质量.
本文结合现有研究的优缺点,针对移动传感数据的特点来研究MCS在线场景下的激励机制,设计了SQOI框架,旨在指定预算和时间限制下,为任务请求者选取能够提供高质量传感数据的工人.
3 系统模型和效用计算
在本节中,我们将介绍系统模型和质量模型,并且定义了本文所解决的问题.为了更清楚、更简单地理解不同符号的含义,表1给出了文中出现的符号及其描述.

表1 符号说明
3.1 系统模型
首先,考虑一个在线MCS系统,其中包含了一些用户和一个中心化平台.任务请求者向平台发布了一系列传感任务T={1,2,…,|T|},同时设置了预算B和活动周期D,前者规定了支付给工人的报酬上限,后者规定任务需要在指定时间内完成.平台拥有一些工人W={1,2,…,|W|},这些工人的移动设备上都安装了MCS的应用程序.每个工人存在两种状态:上线和离线.当工人设备上的MCS程序正在运行,其处于上线状态,准备参与任务;反之,当程序关闭后,其处于离线状态,无法参与任务.
由于涉及到金钱激励,本文将任务与工人的匹配视作一个在线竞价过程.图1具体描述了整个在线MCS系统的执行流程.首先MCS平台对外发布这些传感任务.当工人j上线后,决定是否参与任务,如果选择参与,向平台提交他的请求,包括报价bj、上线时间olj、离线时间ofj和执行的任务集T(j).接着平台根据工人的请求,在无法了解工人的情况下,决定是否聘用该工人.为了维护工人的权益,该决定是不可撤销的.最后如果工人被选中,他需要执行任务并提交自己的传感数据.平台将赋予其一笔报酬pj.该过程将不断重复,直到累计报酬超出预算或任务过期为止.

图1 MCS的执行流程

3.2 质量模型
工人分配到传感任务后,需要在规定时间内提交传感数据.本文考虑一种普遍的场景,即请求者需要第三方平台来判断任务的结果和工人的表现.如环境噪音、温度检测这类传感任务,请求者需要采集一段时间内不同地点的数据,且事先无法得知标准值.在这种情况下,他需要MCS平台发布任务收集数据,并为每个任务预估出较为精确的结果.


(1)
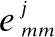
(2)

3.3 效用计算
本文站在请求者的角度上研究问题,即在固定的活动周期内,工人以在线的形式请求执行任务,平台需要在有限的预算内选择能够提供高质量传感数据的工人.用Ms表示第s阶段平台选择的工人,于是请求者每个阶段的效用为:
(3)
由于Bs是常量,所以目标函数可以转变为:
(4)
(5)
平台制定有效的激励机制来尽可能地提升请求者的效用,同时需要满足以下几个性质:
1)预算可行性:累计的任务报酬不能超过预算限制,如公式(5)所示.

4)计算效率:提出的激励机制可以在多项式时间内计算.
4 多阶段质量感知的在线激励机制框架设计
本节主要介绍SQOI的具体框架设计.在3.1节,整个众包活动周期被分成了多个阶段,平台需要在每个阶段对上线的工人进行选择、给予合适的报酬、评估数据质量并更新相关参数,为下一阶段做参考.所以SQOI把每个阶段又分为阶段性工人选择、质量预估和参数更新3个模块.由于各个阶段的处理方式一致,为了简化符号,下文统一将上标s忽略.
4.1 阶段性工人选择
在离线场景下,所有工人事先提交信息,平台计算这些工人的服务质量后,选取前k个质量最高的工人即可最大化请求者的效用.而在线场景下,工人以随机的形式一个接一个地上线,平台无法获得全局信息,这种情况类似于经典的秘书问题.本文采用阶段性工人选择算法,每个阶段输入阈值θ作为工人的选择标准.在当前阶段结束后,统计该阶段中所有在线工人的报价和预估的质量,计算后更新θ,作为下一阶段的输入.首阶段的阈值由平台设定.

算法1.Phased Worker Selection
输入:任务集T,预算B,活动周期D,阈值θ
输出:分配结果M,支付报酬P
初始化M←φ,M′←φ,d←1
1.whiled≤Ddo
2.ifwjarriving at time stepdthen

5. end if
6.M′←M′∪{j}
7.end if
8.ifd=Dthen
9. obtain all the dataXworkers submit
10.tr,E←Quality_Estimate(M,X)
11.θ←Parameter_Update(tr,X,M,M′)
12.end if
13.t←t+1
14.end while
15.returnM,P,θ
4.2 质量预估
在每个阶段末,平台收集完工人提交的数据后,如果事先得知每个任务的真实结果,那么可以判断工人提交的传感数据是否通过标准,从而评估工人的服务质量.在本文的场景下,请求者无法给定每个任务的正确答案,即tri是一个隐藏变量,这导致了工人的效用矩阵无法直接获取.因此平台需要根据工人提交的传感数据推测出最接近的答案.假设每个阶段平台能够收集到大量的数据,那么在参数未知的情况下,可以借助期望最大化(EM)算法的思想求得tri的最大似然估计,从而预估出真实数据所在的区间[6].

(6)

(7)
同时,可以得到每个区间的先验估计:
(8)

(9)
即:
(10)
由于EM算法是一个迭代的方法,该模块会重复计算每个工人的效用矩阵和每个任务的真实结果分布,直至参数收敛,最终得到一个准确的结果.

算法2.Quality Estimate
输入:匹配集M,数据集X
输出:任务真实结果分布tr,工人的效用矩阵E,

1.fori∈Tdo
2. form∈σdo
4. end for
5.end for
6.whiletr,Edid not converge do
7. for m∈σ
8. calculatetlmaccording to equation (8)
9. end for
10. for j ∈Mdo

12. form,n∈σdo
14. end for
15. end for
16. fori∈Tdo
18. form∈σdo
20. end for
21. end for
22.end while
23.returntr,E
4.3 参数更新
得到每个任务的真实区间概率和每个工人的效用矩阵后,平台需要更新相关参数.具体由算法3所示,主要分为两部分,第1部分更新了工人的动态质量和静态质量(1-11行).第2部分根据采样集M′中工人质量和报价计算出一个新的阈值θ(12-16行).其中参数δ由平台设置,用来控制θ的大小,如果δ较小,θ变大,下一阶段可以选择的工人可能变少,导致阶段任务分配率降低.反之δ较大,选择工人的标准降低,可能造成数据质量下降,浪费了预算.
算法3.Parameter Update
输入:真实结果分布tr,数据集X,匹配集M,采样集M′
输出:下一个阶段阈值θ
1. for(T(j),j)∈M,i∈T(j)do
2. get the intervalnofxi,j
4.αj←αj+1
5. else
6.βj←βj+1
7. end if
8. end for
9. forj∈Wdo
10. updatedqj,sqjfor next stage
11. end for
12.J←φ,sum←0,k←argmaxj∈M′(dqjsqj|T(j)|/bj)
13. while ∑j∈J∪{k}bj≤Bdo
14.J←J∪{k},sum←sum+dqksqk|T(k)|
15.k←argmaxj∈M′-J(dqjsqj|T(j)|/bj)
16.end while
17.returnsum/δB
4.4 理论证明
这一部分主要证明SQOI具备预算可行性、个体合理性、真实性以及计算效率.
定理1.SQOI具备预算可行性.
证明:SQOI将整个众包活动周期分为多个阶段.同时每个阶段都包含有限的预算(2s-1B/2[log2D]).在算法1的第3行,当一个工人上线并提交他的报价后,平台会比较当前阶段剩余预算是否高于工人的预计报酬, 如果前者低于后者,即使工人满足质量标准也不会分配任务.因此框架满足预算可行性.
定理2.SQOI具备个体合理性.
定理3.SQOI具备真实性.


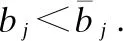
所以在任何情况下,工人在虚假报价下的效用始终不会超过真实报价下的效用,即SQOI具备真实性.
定理4.SQOI具备计算效率.
证明:由于SQOI框架是在线运行的,所以需要考虑每个阶段的复杂度.假设平台的工人数为|W|,任务数为|T|.算法1的工人选择阶段最多需要执行|W|次.在阶段末,|σ|表示数据区间总数,则运行质量评估模块(算法2)最多需要|W‖T‖σ|次迭代.|σ|由平台设置,可以将其作为一个常量来对待,则复杂度为O(|W‖T|).在参数更新模块(算法3),1-11行每个工人需要运行|T(j)|次,即最多需要O(|W‖T|).在12-16行的阈值计算部分,最多需要运行|W|log|W|次.因此,每个阶段的时间复杂度为O(|W‖T|),SQOI具备计算效率.
5 实验分析
本节通过实验来验证SQOI在不同参数下的表现和其在提升请求者效用上的有效性.
5.1 实验设置


表2 实验参数设置
本文设计了3个实验.第1个实验研究了SQOI在不同工人到达率下对效用的影响.第2个实验研究了SQOI参数更新模块的输入参数δ对效用的影响.第3个实验将阶段离线算法(Offline)和在线随机算法(Random)作为基线算法,同SQOI进行对比.在阶段离线算法中,平台能够事先得到各个阶段的工人上线时间、报价和服务质量,然后选择效用最高的k个工人.在线随机算法则是在各个时刻随机选择上线的工人.
5.2 实验结果
首先本文研究了在相同环境下,不同到达率对效用的影响.由图2所示,当用户到达率增加,整体效用增大.同时当到达率在较高的区间内,高预算可以得到更大的效用值.因为工人参与任务的积极性一旦变高,平台可以在初期阶段收集充足的传感数据和采样集,对每个在线工人的质量有更为准确的评估,所以算法1在后期阶段可以选择高质量的工人集,提高请求者的效用.

图2 工人到达率λ对效用的影响
接着本文针对算法3的输入参数δ进行研究.固定预算为2000,比较到达率不同时,参数δ对算法性能的影响.由图3所示,随着δ的增长,整体效用在逐渐降低,同时λ越大时,效用下降的速率也越快.这是由于每个阶段的筛选工人的阈值θ不断下降,导致一些低质量高报价工人可以被选中,最终总效用下降.可见在线场景中,工人参与度较高的情况下,增加δ会降低请求者的效用.
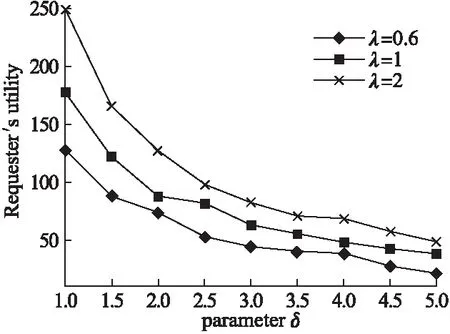
图3 参数δ对效用的影响
最后本文将SQOI与阶段离线算法和在线随机算法进行比较.从图4可以看出,随着请求者预算的增加,离线算法由于在分配前事先获取了所有工人的信息,其表现是最优的.而SQOI的曲线始终位于离线算法和随机算法之间,且远高于后者.所以本文提出的方法比起在线随机算法在提高请求者效用上有着显著的优势.

图4 不同算法的效用对比
6 总结与展望
本文考虑了预算与时间约束下的移动众包在线激励机制问题,提出了一种多阶段质量感知的在线激励机制SQOI,通过增量学习的方式将整个众包活动周期分为多个阶段,每个阶段集成了工人选择、质量评估和参数更新模块.在缺少标准数据的情况下,为请求者尽可能地提供高质量的传感数据.同时,本文证明了SQOI具有预算可行性,个体合理性,真实性和计算效率.最后通过实验进一步说明该机制在提升数据质量上的可行性.
然而,SQOI还存在着以下几点问题.首先,本文考虑的是同质任务,即任务类型相同,且所有任务由请求者同时发布,所以SQOI不适用于异质任务的分配.其次,SQOI在工人低参与度的场景下,由于每个阶段平台收集的数据较少,会影响到算法的性能.在未来的工作中,我们会根据这些问题,进一步完善SQOI的模型和算法.

